math problem solving arithmetic sequence

Free Mathematics Tutorials

• Math Problems
• Algebra Questions and Problems
• Graphs of Functions, Equations, and Algebra
• Free Math Worksheets to Download
• Analytical Tutorials
• Solving Equation and Inequalities
• Online Math Calculators and Solvers
• Free Graph Paper
• Math Software
• The Applications of Mathematics in Physics and Engineering
• Exercises de Mathematiques Utilisant les Applets
• Calculus Tutorials and Problems
• Calculus Questions With Answers
• Free Calculus Worksheets to Download
• Geometry Tutorials and Problems
• Online Geometry Calculators and Solvers
• Free Geometry Worksheets to Download
• Trigonometry Tutorials and Problems for Self Tests
• Free Trigonometry Questions with Answers
• Free Trigonometry Worksheets to Download
• Elementary Statistics and Probability Tutorials and Problems
• Mathematics pages in French
• About the author
• Primary Math
• Middle School Math
• High School Math
• Free Practice for SAT, ACT and Compass Math tests

Arithmetic Sequences Problems with Solutions

Arithmetic sequences are used throughout mathematics and applied to engineering, sciences, computer sciences, biology and finance problems. A set of problems and exercises involving arithmetic sequences, along with detailed solutions are presented.

Review of Arithmetic Sequences

The formula for the n th term a n of an arithmetic sequence with a common difference d and a first term a 1 is given by \[ a_n = a_1 + (n - 1) d \] The sum s n of the first n terms of an arithmetic sequence is defined by \[ s_n = a_1 + a_2 + a_3 + ... + a_n \] and is is given by \[ s_n = \dfrac{n (a_1 + a_n)}{2} \] Arithmetic Series Online Calculator . An online calculator to calculate the sum of the terms in an arithmetic sequence.

Problems with Solutions

The first term of an arithmetic sequence is equal to 6 and the common difference is equal to 3. Find a formula for the n th term and the value of the 50 th term Solution to Problem 1: Use the value of the common difference d = 3 and the first term a 1 = 6 in the formula for the n th term given above \( a_n = a_1 + (n - 1) d \\ = 6 + 3 (n - 1) \\ = 3 n + 3 \) The 50 th term is found by setting n = 50 in the above formula. \[ a_{50} = 3 (50) + 3 = 153 \]

The first term of an arithmetic sequence is equal to 200 and the common difference is equal to -10. Find the value of the 20 th term Solution to Problem 2: Use the value of the common difference d = -10 and the first term a 1 = 200 in the formula for the n th term given above and then apply it to the 20 th term a 20 = 200 + (-10) (20 - 1 ) = 10

An arithmetic sequence has a common difference equal to 10 and its 6 th term is equal to 52. Find its 15 th term. Solution to Problem 3: We use the n th term formula for the 6 th term, which is known, to write a 6 = 52 = a 1 + 10 (6 - 1 ) The above equation allows us to calculate a 1 . a 1 = 2 Now that we know the first term and the common difference, we use the n th term formula to find the 15 th term as follows. a 15 = 2 + 10 (15 - 1) = 142

An arithmetic sequence has a its 5 th term equal to 22 and its 15 th term equal to 62. Find its 100 th term. Solution to Problem 4: We use the n th term formula for the 5 th and 15 th terms to write a 5 = a 1 + (5 - 1 ) d = 22 a 15 = a 1 + (15 - 1 ) d = 62 We obtain a system of 2 linear equations where the unknown are a 1 and d. Subtract the right and left term of the two equations to obtain 62 - 22 = 14 d - 4 d Solve for d. d = 4 Now use the value of d in one of the equations to find a 1 . a 1 + (5 - 1 ) 4 = 22 Solve for a 1 to obtain. a 1 = 6 Now that we have calculated a 1 and d we use them in the n th term formula to find the 100 th formula. a 100 = 6 + 4 (100 - 1 )= 402

Find the sum of all the integers from 1 to 1000. Solution to Problem 5: The sequence of integers starting from 1 to 1000 is given by 1 , 2 , 3 , 4 , ... , 1000 The above sequence has 1000 terms. The first term is 1 and the last term is 1000 and the common difference is equal to 1. We have the formula that gives the sum of the first n terms of an arithmetic sequence knowing the first and last term of the sequence and the number of terms (see formula above). s 1000 = 1000 (1 + 1000) / 2 = 500500

Find the sum of the first 50 even positive integers. Solution to Problem 6: The sequence of the first 50 even positive integers is given by 2 , 4 , 6 , ... The above sequence has a first term equal to 2 and a common difference d = 2. We use the n th term formula to find the 50 th term a 50 = 2 + 2 (50 - 1) = 100 We now the first term and last term and the number of terms in the sequence, we now find the sum of the first 50 terms s 50 = 50 (2 + 100) / 2 = 2550

Find the sum of all positive integers, from 5 to 1555 inclusive, that are divisible by 5. Solution to Problem 7: The first few terms of a sequence of positive integers divisible by 5 is given by 5 , 10 , 15 , ... The above sequence has a first term equal to 5 and a common difference d = 5. We need to know the rank of the term 1555. We use the formula for the n th term as follows 1555 = a 1 + (n - 1 )d Substitute a 1 and d by their values 1555 = 5 + 5(n - 1 ) Solve for n to obtain n = 311 We now know that 1555 is the 311 th term, we can use the formula for the sum as follows s 311 = 311 (5 + 1555) / 2 = 242580

Find the sum S defined by \[ S = \sum_{n=1}^{10} (2n + 1 / 2) \] Solution to Problem 8: Let us first decompose this sum as follows \( S = \sum_{n=1}^{10} (2n + 1 / 2) \) \( = 2 \sum_{n=1}^{10} n + \sum_{n=1}^{10} (1/2) \) The term ∑ n is the sum of the first 10 positive integers. The 10 first positive integers make an arirhmetic sequence with first term equal to 1, it has n = 10 terms and its 10 th term is equal to 10. This sum is obtained using the formula s n = n (a 1 + a n ) / 2 as follows 10(1+10)/2 = 55 The term ∑ (1 / 2) is the addition of a constant term 10 times and is given by 10(1/2) = 5 The sum S is given by S = 2(55) + 5 = 115

Answer the following questions related to arithmetic sequences: a) Find a 20 given that a 3 = 9 and a 8 = 24 b) Find a 30 given that the first few terms of an arithmetic sequence are given by 6,12,18,... c) Find d given that a 1 = 10 and a 20 = 466 d) Find s 30 given that a 10 = 28 and a 20 = 58 e) Find the sum S defined by \[ S = \sum_{n=1}^{20}(3n - 1 / 2) \] f) Find the sum S defined by \[ S = \sum_{n=1}^{20}0.2 n + \sum_{j=21}^{40} 0.4 j \]

Solutions to Above Exercises

a) a 20 = 60 b) a 30 = 180 c) d = 24 d) s 30 = 1335 e) 1380 f) 286

More References and links

• Geometric Sequences Problems with Solutions
• math problems with detailed solutions
• Math Tutorials and Problems

POPULAR PAGES

• Math Problems, Questions and Online Self Tests
• Arithmetic Sequences Online Calculator
• Math Word Problems with Solutions and Answers for Grade 10
• High School Math (Grades 10, 11 and 12) - Free Questions and Problems With Answers

privacy policy

• + ACCUPLACER Mathematics
• + ACT Mathematics
• + AFOQT Mathematics
• + ALEKS Tests
• + ASVAB Mathematics
• + ATI TEAS Math Tests
• + Common Core Math
• + DAT Math Tests
• + FSA Tests
• + FTCE Math
• + GED Mathematics
• + Georgia Milestones Assessment
• + GRE Quantitative Reasoning
• + HiSET Math Exam
• + HSPT Math
• + ISEE Mathematics
• + PARCC Tests
• + Praxis Math
• + PSAT Math Tests
• + PSSA Tests
• + SAT Math Tests
• + SBAC Tests
• + SIFT Math
• + SSAT Math Tests
• + STAAR Tests
• + TABE Tests
• + TASC Math
• + TSI Mathematics
• + ACT Math Worksheets
• + Accuplacer Math Worksheets
• + AFOQT Math Worksheets
• + ALEKS Math Worksheets
• + ASVAB Math Worksheets
• + ATI TEAS 6 Math Worksheets
• + FTCE General Math Worksheets
• + GED Math Worksheets
• + 3rd Grade Mathematics Worksheets
• + 4th Grade Mathematics Worksheets
• + 5th Grade Mathematics Worksheets
• + 6th Grade Math Worksheets
• + 7th Grade Mathematics Worksheets
• + 8th Grade Mathematics Worksheets
• + 9th Grade Math Worksheets
• + HiSET Math Worksheets
• + HSPT Math Worksheets
• + ISEE Middle-Level Math Worksheets
• + PERT Math Worksheets
• + Praxis Math Worksheets
• + PSAT Math Worksheets
• + SAT Math Worksheets
• + SIFT Math Worksheets
• + SSAT Middle Level Math Worksheets
• + 7th Grade STAAR Math Worksheets
• + 8th Grade STAAR Math Worksheets
• + THEA Math Worksheets
• + TABE Math Worksheets
• + TASC Math Worksheets
• + TSI Math Worksheets
• + AFOQT Math Course
• + ALEKS Math Course
• + ASVAB Math Course
• + ATI TEAS 6 Math Course
• + CHSPE Math Course
• + FTCE General Knowledge Course
• + GED Math Course
• + HiSET Math Course
• + HSPT Math Course
• + ISEE Upper Level Math Course
• + SHSAT Math Course
• + SSAT Upper-Level Math Course
• + PERT Math Course
• + Praxis Core Math Course
• + SIFT Math Course
• + 8th Grade STAAR Math Course
• + TABE Math Course
• + TASC Math Course
• + TSI Math Course
• + Number Properties Puzzles
• + Algebra Puzzles
• + Geometry Puzzles
• + Intelligent Math Puzzles
• + Ratio, Proportion & Percentages Puzzles
• + Other Math Puzzles

How to Solve Arithmetic Sequences? (+FREE Worksheet!)

Do you want to know how to solve Arithmetic Sequences problems? you can do it in few simple and easy steps.

Related Topics

• How to Solve Finite Geometric Series
• How to Solve Infinite Geometric Series
• How to Solve Geometric Sequences

Step by step guide to solve Arithmetic Sequences problems

• A sequence of numbers such that the difference between the consecutive terms is constant is called arithmetic sequence. For example, the sequence \(6, 8, 10, 12, 14\), … is an arithmetic sequence with common difference of \(2\).
• To find any term in an arithmetic sequence use this formula: \(\color{blue}{x_{n}=a+d(n-1)}\)
• \(a =\) the first term ,\(d =\) the common difference between terms , \(n =\) number of items

Arithmetic Sequences – Example 1:

Find the first three terms of the sequence. \(a_{17}=38,d=3\)

First, we need to find \(a_{1}\) or a. Use arithmetic sequence formula: \(\color{blue}{x_{n}=a+d(n-1)}\) If \(a_{8}=38\), then \(n=8\). Rewrite the formula and put the values provided: \(x_{n}=a+d(n-1)→38=a+3(3-1)=a+6\), now solve for \(a\). \(38=a+6→a=38-6=32\), First three terms: \(32,35,38\)

The Absolute Best Books to Ace Pre-Algebra to Algebra II

The Ultimate Algebra Bundle From Pre-Algebra to Algebra II

Arithmetic sequences – example 2:.

Given the first term and the common difference of an arithmetic sequence find the first five terms. \(a_{1}=18,d=2\)

Use arithmetic sequence formula: \(\color{blue}{x_{n}=a+d(n-1)}\) If \(n=1\) then: \(x_{1}=18+2(1)→x_{1}=18\) First five terms: \(18,20,22,24,26\)

Arithmetic Sequences – Example 3:

Given the first term and the common difference of an arithmetic sequence find the first five terms. \(a_{1}=24,d=2\)

Use arithmetic sequence formula: \(\color{blue}{x_{n}=a+d(n-1)}\) If \(n=1\) then: \(x_{1}=22+2(1)→x_{1}=24\) First five terms: \(24,26,28,30,32\)

The Best Book to Help You Ace Pre-Algebra

Pre-Algebra for Beginners The Ultimate Step by Step Guide to Preparing for the Pre-Algebra Test

Arithmetic sequences – example 4:.

Find the first five terms of the sequence. \(a_{17}=152,d=4\)

First, we need to find \(a_{1}\) or \(a\). Use arithmetic sequence formula: \(\color{blue}{x_{n}=a+d(n-1)}\) If \(a_{17}=152\), then \(n=17\). Rewrite the formula and put the values provided: \(x_{n}=a+d(n-1)→152=a+4(17-1)=a+64\), now solve for \(a\). \(152=a+64→a=152-64=88\), First five terms: \(88,92,96,100,104\)

Given the first term and the common difference of an arithmetic sequence find the first five terms and the explicit formula.

• \(\color{blue}{a_{1} = 24, d = 2}\)
• \(\color{blue}{a_{1} = –15, d = – 5}\)
• \(\color{blue}{a_{1} = 18, d = 10}\)
• \(\color{blue}{a_{1 }= –38, d = –100}\)

Download Arithmetic Sequences Worksheet

• First Five Terms \(\color{blue}{: 24, 26, 28, 30, 32, Explicit: a_{n} = 22 + 2n}\)
• First Five Terms \(\color{blue}{: –15, –20, –25, –30, –35, Explicit: a_{n} = –10 – 5n}\)
• First Five Terms \(\color{blue}{: 18, 28, 38, 48, 58, Explicit: a_{n} = 8 + 10n}\)
• First Five Terms \(\color{blue}{: –38, –138, –238, –338, –438, Explicit: a_{n} = 62 – 100n}\)

The Greatest Books for Students to Ace the Algebra

Pre-Algebra Exercise Book A Comprehensive Workbook + PreAlgebra Practice Tests

Pre-algebra in 10 days the most effective pre-algebra crash course, college algebra practice workbook the most comprehensive review of college algebra, high school algebra i a comprehensive review and step-by-step guide to mastering high school algebra 1, 10 full length clep college algebra practice tests the practice you need to ace the clep college algebra test.

by: Effortless Math Team about 4 years ago (category: Articles , Free Math Worksheets )

Effortless Math Team

Related to this article, more math articles.

• Top Math Strategies for Better Scores on the GRE
• The Great Math Tour: Exploring the World of Circle Graphs
• How to Find Slope From a Graph?
• 4th Grade KAP Math Worksheets: FREE & Printable
• How To Get A Perfect Score Of 800 On SAT Math?
• 3rd Grade ISASP Math Worksheets: FREE & Printable
• 8th Grade Common Core Math FREE Sample Practice Questions
• Using Strip Diagrams to Represent Fractions
• How to Use Strip Models to Identify Equivalent Expressions?
• SAT And ACT Tests Hacks and Tips

What people say about "How to Solve Arithmetic Sequences? (+FREE Worksheet!) - Effortless Math: We Help Students Learn to LOVE Mathematics"?

No one replied yet.

Leave a Reply Cancel reply

You must be logged in to post a comment.

Pre-Algebra Practice Workbook The Most Comprehensive Review of Pre-Algebra

Algebra i practice workbook the most comprehensive review of algebra 1, algebra ii practice workbook the most comprehensive review of algebra 2, algebra i for beginners the ultimate step by step guide to acing algebra i, algebra ii for beginners the ultimate step by step guide to acing algebra ii, pre-algebra tutor everything you need to help achieve an excellent score.

• ATI TEAS 6 Math
• ISEE Upper Level Math
• SSAT Upper-Level Math
• Praxis Core Math
• 8th Grade STAAR Math

Limited time only!

Save Over 45 %

It was $89.99 now it is $49.99

Login and use all of our services.

Effortless Math services are waiting for you. login faster!

Register Fast!

Password will be generated automatically and sent to your email.

After registration you can change your password if you want.

• Math Worksheets
• Math Courses
• Math Topics
• Math Puzzles
• Math eBooks
• GED Math Books
• HiSET Math Books
• ACT Math Books
• ISEE Math Books
• ACCUPLACER Books
• Premium Membership
• Youtube Videos
• Google Play
• Apple Store

Effortless Math provides unofficial test prep products for a variety of tests and exams. All trademarks are property of their respective trademark owners.

• Bulk Orders
• Refund Policy

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons
• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

8.1: Arithmetic Sequences

• Last updated
• Save as PDF
• Page ID 83157

• Jennifer Freidenreich
• Diablo Valley College

The following sequence of numbers has a pattern you are bound to recognize:

\(2, 4, 6, 8, 10, 12, 14, 16, 18, …\)

Likely, you would describe the sequence in words: the sequence of even numbers. Alternatively, can we describe the sequence mathematically? That is, can we describe the pattern of the sequence of even numbers using a formula? Absolutely! This section will explore arithmetic sequences, how to identify them, mathematically describe their terms, and the relationship between arithmetic sequences and linear functions. Let’s get started!

Definition: Sequence

A sequence is a list of numbers: \(a_1 , a_2, a_3, a_4 , … , a_n, … \) A sequence can be a finite or infinite list. We call \(a_1\) the first term, \(a_2\) the second term, and \(a_n\) the “general term” or the \(n^{\text{th}}\) term. Sequences have a pattern. We describe the pattern in the general term \(a_n\).

For the sequence of even numbers: \(2, 4, 6, 8, 10, …\) the general term \(a_n = 2n\).

The general term \(a_n\) of a sequence is simply a function of \(n\), indicated above as \(f(n)\), where \(n\) is a natural number (or whole number if \(n\) starts with zero).

Example 8.1.1

In the sequence of even numbers, what is the \(20^{\text{th}}\) term in the sequence?

The general term of the sequence of even numbers is \(a_n = 2n\). Since \(n =\) the term number, we are asked to find \(a_{20}\).

\(\begin{array}&& a_{20} = 2(20) = 40 &\text{Plug in the term-number \(n=20\) into the formula \(a_n=2n\)} \end{array}\)

Answer The \(20^{\text{th}}\) term of the sequence of even numbers is the number \(40\).

Definition: Arithmetic Sequence

If the sequence: \(a_1, a_2, a_3, a_4 , … , a_{n−1}, a_n, …\) exhibits a pattern such that

\[a_n − a_{n−1} = d\]

For all \(n\), then the real number \(d\) is called the common difference , and the sequence is an arithmetic sequence .

Example 8.1.2

A sequence is given. If the sequence is an arithmetic sequence, give the common difference. If the sequence is not an arithmetic sequence, explain how it fails to be arithmetic.

• \(25, 32, 39, 46, 53, 60, …\)

\(2, 4, 8, 16, 32, …\)

\(3^2 , 3^4, 3^6, 3^8, 3^{10}, …\)

\(0, 1, 0, 1, 0, 1, …\)

• Is the sequence

\(25, 32, 39, 46, 53, 60, … \)

an arithmetic sequence?

\(\begin{array} &a_2 − a_1 &= 32 − 25 &= \textcolor{red}{7} \\ a_3 − a_2 &= 39 − 32 &= \textcolor{red}{7} \\a_4 − a_3 &= 46 − 39 &= \textcolor{red}{7} \\a_5 − a_4 &= 53 − 46 &= \textcolor{red}{7} \\a_6 − a_5 &= 60 − 53 &= \textcolor{red}{7} \end{array}\)

The sequence is arithmetic and the common difference is \(7\).

\(\begin{array} &a_2 − a_1 &= 4 − 2 &= \textcolor{red}{2} \\ a_3 − a_2 &= 8 − 4 &= \textcolor{red}{4} \\a_4 − a_3 &= 16 − 8 &= \textcolor{red}{8} \\a_5 − a_4 &= 32 − 16 &= \textcolor{red}{16} \\ &&\textcolor{red}{2 \neq 4 \neq 8 \neq 16} \end{array}\)

The sequence is not arithmetic. \(a_n − a_{n-1}\) does not yield a common difference.

\(\begin{array} &3^4 − 3^2 &= 3^2 (3^2 − 1) &= 9 \cdot 8 &= \textcolor{red}{72} \\ 3^6 − 3^4 &= 3^4 (3^2 − 1) &= 81 \cdot 8 &= \textcolor{red}{648} \end{array}\)

Since \(a_3 − a_2 \neq a_2 − a_1\), we conclude the sequence is not arithmetic.

\(\begin{array} 1-0 &= \textcolor{red}{1} \\ 0-1 &= \textcolor{red}{-1} \end{array}\)

Since \(a_3 − a_2 \neq a_2 − a_1\), the sequence is not arithmetic.

Find the General Term of an Arithmetic Sequence

If a sequence is arithmetic, the general term \(a_n\) is determined using the common difference, \(d\), of the sequence. Functions of the form \(y = mx+b\), known as linear functions, have a strong relationship to arithmetic sequences. The slope \(m\) of a linear function is equivalent to the common difference \(d\) of an arithmetic sequence. Let’s compare arithmetic sequences to linear functions to build \(a_n\), the general term of an arithmetic sequence.

Example 8.1.3

Find the general term \(a_n\) of each arithmetic sequence:

• \(4, 7, 10, 13, 16, …\)
• \(100, 80, 60, 40, 20, …\)

We will create a table of values for each sequence. The first column will be the term number, \(n\), starting with \(n = 1\). The second column will list the terms of the sequence. The common difference is shown on the side of the second column.

• The sequence \(4, 7, 10, 13, 16, …\) has the common difference \(d = 3\). But it’s also the slope \(m\) of the linear function \(f(x) = mx + b\).

\[m = \dfrac{\delta y}{\delta x} = \dfrac{a_n − a_{n-1}}{n − (n − 1))} = \dfrac{d}{1} = d\]

The above table essentially mimics any linear function, \(f(x) = mx+b\).

• Instead of \(x\), sequences use \(n\)−values.
• Instead of \(m =\) slope in linear functions, sequences use \(d =\) common difference.
• Instead of \(b\), a sequence notates the same value with \(a_0\).

If \(a_1\) denotes the first term of a sequence, then the general term of a sequence is:

\[a_n = f(n) = d \cdot n + a_0\]

To find the general term, \(a_n\), we will need to find the value \(a_0\). There are several ways to do this, but perhaps the simplest is to create an extra row where \(n = 0\), then use the common difference to find \(a_0\). The common difference pattern is maintained and \(a_0 + d = a_1\).

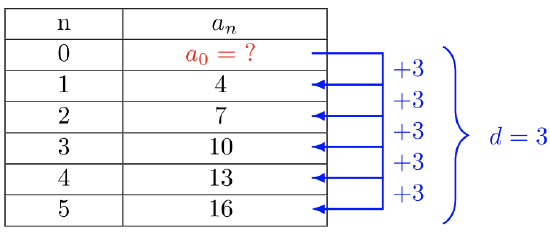
Find the value \(a_0\):

\(\begin{array} &&a_0 + 3 &= 4 \\&a_0 + 3 − 3 &= 4 − 3 \\&a_0 &= 1\end{array}\)

The general term of the sequence is:

\(a_n = 3n + 1\)

• Use the same strategy for Example \(8.1.3\)a to solve Example \(8.1.3\)b. Create a table, find the common difference, \(d\), and find the \(a_0\) term of the sequence \(100, 80, 60, 40, 20, …\)

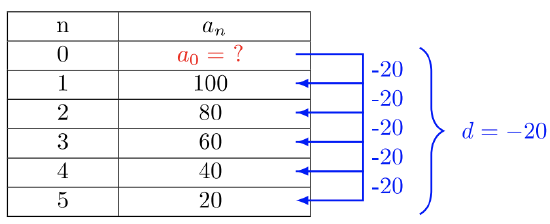
The common difference \(d = −20\). Find the value \(a_0\).

\(\begin{array} &&a_0 − 20 &= 100 \\ &a_0 − 20 + 20 &= 100 + 20 \\ &a_0 &= 120 \end{array}\)

\(a_n = −20n + 120\)

Try It! (Exercises)

For #1-5, the general term of a sequence is given.

• List the first \(5\) terms of the sequence: \(a_1, a_2, a_3, a_4, a_5\).
• Is the sequence arithmetic?
• \(a_n = n^2\)
• \(a_n = 4 − 5n\)
• \(a_n = 2^n\)
• \(a_n = \dfrac{1}{2}n\)
• \(a_n = 0.3n + 1\)

For #6-9, a table of values is given. State the general term, \(a_n\), of the arithmetic sequence.

For #10-15, find the general term of the arithmetic sequence. Assume the first term is \(a_1\).

• \(8, 15, 22, 29, …\)
• \(110, 85, 60, 35, …\)
• \(9, 7.4, 5.8, 4.2, …\)
• \(\dfrac{17}{2} , 8, \dfrac{15}{2} , 7, …\)
• \(−20, −8, 4, 16, 28, …\)
• \(4 \dfrac{1}{2} , 5 \dfrac{1}{4} , 6, 6 \dfrac{3}{4} , …\)

For #16-20, an arithmetic sequence is described. Find the general term \(a_n\).

• The arithmetic sequence has common difference \(d=8\). The first term \(a_1 = 28\).
• The arithmetic sequence has first term \(a_1 = 40\) and second term \(a_2 = 36\).
• The arithmetic sequence has first term \(a_1 = 6\) and third term \(a_3 = 24\).
• The arithmetic sequence has common difference \(d = −2\) and third term \(a_3 = 15\).
• The arithmetic sequence has common difference \(d = 3.6\) and fifth term \(a_5 = 10.2\).
• Explain how the formula for the general term given in this section: \(a_n = d \cdot n + a_0\) is equivalent to the following formula: \(a_n = a_1 + d(n − 1)\)
• Some sequences have a finite number of terms. Find the number of terms in the finite arithmetic sequence: \(3, 17, 31, … ,143\)
• Some sequences have a finite number of terms. Find the number of terms in the finite arithmetic sequence: \(80, 69, 58, … , −52\)
• Create a formula for finding the number of terms a finite arithmetic sequence when given the first and the last term of the sequence. Assume the first term is \(a_1\) and the last term is \(a_k\).

• Daily Games
• Strategy and Puzzles
• Vocabulary Games
• Junior Edition Games
• All problems
• High School Math
• MAML Problems
• Calculus Problems
• Loony Physics
• Pro Problems
• Getting Started
• Pro Control Panel
• Virtual Classroom
• Play My Favorites
• Select My Favorites

Arithmetic Sequence Problems

There are many problems we can solve if we keep in mind that the  n th term of an arithmetic sequence can be written in the following way: a n  = a 1 +(n - 1)d Where a 1  is the first term, and  d  is the common difference. For example, if we are told that the first two terms add up to the fifth term, and that the common difference is 8 less than the first term we can take this equation: a 1  + a 2  = a 5 and rewrite it as follows: a 1  + [a 1  + d] = [a 1  + 4d] This leads to a 1  = 3d. Combine this with d = a 1  - 8, and we have: a 1  = 3(a 1  - 8) or a 1  = 12. This leads to d = 4, and from this information, we can find any other term of the sequence.

Blogs on This Site

Or search by topic

Number and algebra

• The Number System and Place Value
• Calculations and Numerical Methods
• Fractions, Decimals, Percentages, Ratio and Proportion
• Properties of Numbers
• Patterns, Sequences and Structure
• Algebraic expressions, equations and formulae
• Coordinates, Functions and Graphs

Geometry and measure

• Angles, Polygons, and Geometrical Proof
• 3D Geometry, Shape and Space
• Measuring and calculating with units
• Transformations and constructions
• Pythagoras and Trigonometry
• Vectors and Matrices

Probability and statistics

• Handling, Processing and Representing Data
• Probability

Working mathematically

• Thinking mathematically
• Mathematical mindsets
• Cross-curricular contexts
• Physical and digital manipulatives

For younger learners

• Early Years Foundation Stage

Advanced mathematics

• Decision Mathematics and Combinatorics
• Advanced Probability and Statistics

Patterns and Sequences Short Problems

Fibonacci Deduction

Leonard writes down a sequence of numbers. Can you find a formula to predict the seventh number in his sequence?

Hexagon Line

How many hexagons are required for the perimeter of the whole shape to have length 1002cm?

Street Lamps

Walking up a steep hill, I pass 10 equally spaced street lamps. How long do I take to walk from the first lamp to the last?

Fruit Line-up

This grocer wants to arrange his fruit in a particular order, can you help him?

Triangular Clock

Trinni rearanges numbers on a clock face so each adjacent pair add up to a triangle number... What number did she put where 6 would usually be?

Printing Error

Every third page number in this book has been omitted. Can you work out what number will be on the last page?

Sliding Robot

A robot moves along the number line. Where will it be after 2011 slides?

Many Matildas

MatildaMatildaMatil... What is the 1000th letter?

How Many Rectangles?

By drawing 5 horizontal and four vertical lines, one can form 12 rectangles. What is the greatest number of rectangles that can be formed by drawing 15 lines?

Night Watchmen

Grannie's watch gains 30 minutes every hour, whilst Grandpa's watch loses 30 minutes every hour. What is the correct time when their watches next agree?

Weekly Problem 51 - 2016 Pegs numbered 1 to 50 are placed in a row. Alternate pegs are knocked down, and this process is repeated. What is the number of the last peg to be knocked down?

Pattern Snake

This pattern repeats every 12 dots. Can you work out what a later piece will be?

What a Coincidence!

Consider two arithmetic sequences: 1998, 2005, 2012,... and 1996, 2005, 2014,... Which numbers will appear in both?

Suit Sequence

A pattern repeats every six symbols. What are the 100th and 101st symbols?

Knights and Knaves

Knights always tell the truth. Knaves always lie. Can you catch these knights and knaves out?

Doubly Consecutive Sums

How many numbers less than 2017 are both the sum of two consecutive integers and the sum of five consecutive integers?

Expanding Pattern

How many squares are needed to continue this pattern?

Can you work out which number will appear directly below 400 in this pattern?

Trolley Park

In a supermarket, there are two lines of tightly packed trolleys. What is the length of one trolley?

Alternating Sum

Given that the number 2008 is the correct answer to a sum, can you find n?

Newspaper Sheets

From only the page numbers on one sheet of newspaper, can you work out how many sheets there are altogether?

If a number is even, halve it; if odd, treble it and add 1. If a sequence starts at 13, what will be the value of the 2008th term?

Repeat a pattern of numbers to form a larger number. Can you find the sum of all the digits?

Collatz-ish

A sequence is generated using these rules. For which values of n is the nth term equal to n?

Math-Exercises .com

   SK    CZ    EN

Math Exercises & Math Problems: Arithmetic Sequence

You might be also interested in:

Math Exercises

• Length Unit Conversion
• Area Unit Conversion
• Volume Unit Conversion
• Weight and Mass Unit Conversion
• Time Unit Conversion
• Speed Unit Conversion
• Physical Quantities Unit Conversion
• Angle Unit Conversion
• Unit Conversion Word Problems
• Sets and Intervals
• Natural Numbers
• Complex Numbers
• Common Multiple and Divisor
• Fractions and Decimals
• Unknown Variable in Formula
• Polynomials
• Formulas, Expending & Factoring
• Algebraic Fractions
• Linear Equations and Inequalities
• Systems of Equations and Inequalities
• Quadratic Equations and Inequalities
• Irrational Equations and Inequalities
• Exponential Equations and Inequalities
• Logarithmic Equations and Inequalities
• Trigonometric Equations and Inequalities
• Equation Word Problems
• Inequality Word Problems
• Linear Function
• Linear Fractional Function
• Quadratic Function
• Power Function
• Exponential Function
• Logarithmic Function
• Trigonometric Functions
• Inverse Function
• Arithmetic Sequence
• Geometric Sequence
• Applications of Sequences
• Infinite Series and Sums
• Limit of a Sequence
• Variations, Permutations, Combinations
• Binomial Theorem
• Combinatorial Expressions
• Combinatorial Equations and Inequalities
• Probability
• Mathematical Statistics
• Perimeter and Area of Plane Figures
• Triangle and Its Properties
• Trigonometry
• Geometric Construction Exercises
• Volume and Surface Area of Solids
• Metric Relations in Space
• Straight Line and Plane
• Relative Position Between Lines and Planes
• Conic Sections
• Sum, Difference and Product of Matrices
• Inverse Matrix
• Rank of a Matrix
• Determinant of a Matrix
• Matrix Equations
• System of Equations Solved by Matrices
• Matrix Word Problems
• Limit of a Function
• Derivative of a Function
• Indefinite Integral
• Definite Integral
• Properties of Functions
• Domain of a Function
• Graph of a Function
• Intersections of Graph with Coordinate Axes
• Evenness and Oddness of a Function
• Continuity of a Function
• Asymptotes of a Function
• Tangent and Normal Line to the Graph of a Function
• Local Extrema of a Function
• Monotonicity of a Function, Stationary Points
• Convexity of a Function, Inflection Points
• Forgot your username?
• Forgot your password?

You can read a gentle introduction to Sequences in Common Number Patterns .

What is a Sequence?

A Sequence is a list of things (usually numbers) that are in order.

Infinite or Finite

When the sequence goes on forever it is called an infinite sequence , otherwise it is a finite sequence

{1, 2, 3, 4, ...} is a very simple sequence (and it is an infinite sequence )

{20, 25, 30, 35, ...} is also an infinite sequence

{1, 3, 5, 7} is the sequence of the first 4 odd numbers (and is a finite sequence )

{4, 3, 2, 1} is 4 to 1 backwards

{1, 2, 4, 8, 16, 32, ...} is an infinite sequence where every term doubles

{a, b, c, d, e} is the sequence of the first 5 letters alphabetically

{f, r, e, d} is the sequence of letters in the name "fred"

{0, 1, 0, 1, 0, 1, ...} is the sequence of alternating 0s and 1s (yes they are in order, it is an alternating order in this case)

When we say the terms are "in order", we are free to define what order that is ! They could go forwards, backwards ... or they could alternate ... or any type of order we want!

A Sequence is like a Set , except:

• the terms are in order (with Sets the order does not matter)
• the same value can appear many times (only once in Sets)

Example: {0, 1, 0, 1, 0, 1, ...} is the sequence of alternating 0s and 1s.

The set is just {0,1}

The curly brackets { } are sometimes called "set brackets" or "braces".

A Sequence usually has a Rule , which is a way to find the value of each term.

Example: the sequence {3, 5, 7, 9, ...} starts at 3 and jumps 2 every time:

As a Formula

Saying " starts at 3 and jumps 2 every time " is fine, but it doesn't help us calculate the:

• 10 th term,
• 100 th term, or
• n th term, where n could be any term number we want.

So, we want a formula with " n " in it (where n is any term number).

So, What Can A Rule For {3, 5, 7, 9, ...} Be?

Firstly, we can see the sequence goes up 2 every time, so we can guess that a Rule is something like "2 times n" (where "n" is the term number). Let's test it out:

Test Rule: 2n

That nearly worked ... but it is too low by 1 every time, so let us try changing it to:

Test Rule: 2n+1

That Works!

So instead of saying "starts at 3 and jumps 2 every time" we write this:

Now we can calculate, for example, the 100th term :

2 × 100 + 1 = 201

But mathematics is so powerful we can find more than one Rule that works for any sequence.

Example: the sequence {3, 5, 7, 9, ...}

We have just shown a Rule for {3, 5, 7, 9, ...} is: 2n+1

And so we get: {3, 5, 7, 9, 11, 13, ...}

But can we find another rule?

How about "odd numbers without a 1 in them" :

And we get: {3, 5, 7, 9, 23, 25, ...}

A completely different sequence!

And we could find more rules that match {3, 5, 7, 9, ...} . Really we could.

So it is best to say "A Rule" rather than "The Rule" (unless we know it is the right Rule).

To make it easier to use rules, we often use this special style:

Example: to mention the "5th term" we write: x 5

So a rule for {3, 5, 7, 9, ...} can be written as an equation like this:

And to calculate the 10th term we can write:

x 10 = 2 n +1 = 2× 10 +1 = 21

Can you calculate x 50 (the 50th term) doing this?

Here is another example:

Example: Calculate the first 4 terms of this sequence:

{a n } = { (-1/n) n }.

Calculations:

• a 1 = (-1/1) 1 = -1
• a 2 = (-1/2) 2 = 1/4
• a 3 = (-1/3) 3 = -1/27
• a 4 = (-1/4) 4 = 1/256

{a n } = { -1, 1/4, -1/27, 1/256, ... }

Special Sequences

Now let's look at some special sequences, and their rules.

Arithmetic Sequences

In an Arithmetic Sequence the difference between one term and the next is a constant .

In other words, we just add some value each time ... on to infinity.

This sequence has a difference of 3 between each number. Its Rule is x n = 3n-2

In General we can write an arithmetic sequence like this:

{a, a+d, a+2d, a+3d, ... }

• a is the first term, and
• d is the difference between the terms (called the "common difference" )

And we can make the rule:

x n = a + d(n-1)

(We use "n-1" because d is not used in the 1st term).

Geometric Sequences

In a Geometric Sequence each term is found by multiplying the previous term by a constant .

This sequence has a factor of 2 between each number. Its Rule is x n = 2 n

In General we can write a geometric sequence like this:

{a, ar, ar 2 , ar 3 , ... }

• r is the factor between the terms (called the "common ratio" )

Note: r should not be 0.

• When r=0 , we get the sequence {a,0,0,...} which is not geometric

And the rule is:

x n = ar (n-1)

(We use "n-1" because ar 0 is the 1st term)

Triangular Numbers

The Triangular Number Sequence is generated from a pattern of dots which form a triangle:

By adding another row of dots and counting all the dots we can find the next number of the sequence.

But it is easier to use this Rule:

x n = n(n+1)/2

• the 5th Triangular Number is x 5 = 5(5+1)/2 = 15 ,
• and the sixth is x 6 = 6(6+1)/2 = 21

Square Numbers

The next number is made by squaring where it is in the pattern.

Rule is x n = n 2

Cube Numbers

The next number is made by cubing where it is in the pattern.

Rule is x n = n 3

Fibonacci Sequence

This is the Fibonacci Sequence

The next number is found by adding the two numbers before it together:

• The 2 is found by adding the two numbers before it (1+1)
• The 21 is found by adding the two numbers before it (8+13)

Rule is x n = x n-1 + x n-2

That rule is interesting because it depends on the values of the previous two terms.

Rules like that are called recursive formulas.

The Fibonacci Sequence is numbered from 0 onwards like this:

Example: term "6" is calculated like this:

x 6 = x 6-1 + x 6-2 = x 5 + x 4 = 5 + 3 = 8

Series and Partial Sums

Now you know about sequences, the next thing to learn about is how to sum them up. Read our page on Partial Sums .

When we sum up just part of a sequence it is called a Partial Sum .

But a sum of an infinite sequence it is called a "Series" (it sounds like another name for sequence, but it is actually a sum). See Infinite Series .

Example: Odd numbers

Sequence: {1, 3, 5, 7, ...}

Series: 1 + 3 + 5 + 7 + ...

Partial Sum of first 3 terms: 1 + 3 + 5

In mathematics, a sequence is an ordered list of numbers or other mathematical objects that follow a particular pattern. Sequences are important in many areas of mathematics, including calculus, analysis, number theory, and discrete mathematics.

We come across sequences in many places in real life. For example, the house numbers in a row, salary in successive years (by a fixed amount or a by a fixed percentage), page numbers of a book, etc represent sequences. Let us learn more about sequences along with their types, rules, formulas, and examples.

What is a Sequence?

A sequence is a list of numbers (or elements) that exhibits a particular pattern. Each element in the sequence is called a term. A sequence can be finite, meaning it has a specific number of terms, or infinite, meaning it continues indefinitely. Sequences can be described in different ways, such as an explicit formula, a recurrence relation, or a table of values.

• An explicit formula gives a direct way to compute each term in the sequence.
• A recurrence relation expresses each term in terms of one or more preceding terms.
• A table of values simply lists the terms in the sequence.

There are several types of sequences in math such as arithmetic sequences, quadratic sequences, geometric sequences, triangular sequences, square number sequences, cube number sequences, and triangular number sequences. Let us learn each of the sequences in detail in the upcoming sections.

Order of the Sequence

The order of a sequence can be either ascending or descending order.

Ascending Order

If the elements of the sequence are in increasing order, then the order of the sequence is ascending.

The above sequence is in ascending order as its terms are "increasing" by 2.

Descending Order

If the elements of the sequence are in decreasing order, then the order of the sequence is descending.

The above sequence is in descending order as its terms are "decreasing" by 4.

Finite and Infinite Sequences

There are two types of sequences: finite sequences and infinite sequences. It is possible to count the number of terms in a finite sequence. An infinite sequence is a sequence that is not finite.

Finite Sequence

A sequence having a finite number of terms is called a finite sequence. For example, a sequence of the number of bounces a ball takes to come to the rest is a finite sequence.

Infinite Sequence

A sequence having an infinite number of terms is called an infinite sequence. For example, a sequence of natural numbers forms an infinite sequence: 1, 2, 3, 4, and so on.

Types of Sequences in Math

There are a few special sequences like arithmetic sequence, geometric sequence, Fibonacci sequence, harmonic sequence, triangular number sequence, square number sequence, and cube number sequence. Apart from these, there can be sequences that follow some other pattern. For example, 2, 9, 28, 65, ... is a sequence in which the numbers can be written as 1 3 + 1, 2 3 + 1, 3 3 + 1, 4 3 + 1,.... and this sequence does not belong to any of the following sequences.

We will discuss these sequences in detail.

Arithmetic Sequence

An arithmetic sequence is a sequence of numbers in which each successive term is a sum of its preceding term and a fixed number. This fixed number is called a common difference . The terms of the arithmetic sequence are of the form a, a+d, a+2d, ....

Example: Mushi put $30 in her piggy bank when she was 7 years old. She increased the amount on her each successive birthday by $3. So, the amount in her piggy bank follows the pattern of $30, $33, $36, and so on. The succeeding terms are obtained by adding a fixed number, that is, $3. This fixed number is called a common difference. It can be positive, negative, or zero.

Quadratic Sequence

We have already seen that if the differences (referred to as first differences) between every two successive terms are the same, then it is called an arithmetic sequence (which is also known as a linear sequence). But if the first differences are NOT the same, and instead, the second differences are the same, then the sequence is known as a quadratic sequence.

Example: The sequence 1, 2, 4, 7, 11, ... is a quadratic sequence because their second differences are the same. Take a look at the figure below.

Geometric Sequence

A geometric sequence is a sequence where every term bears a constant ratio to its preceding term. This ratio is called the " common ratio ". The terms of the geometric sequence are of the form a, ar, ar 2 , ....

Example: Consider an example of geometric sequence: 1, 4, 16, 64, .... Here, 4/1 = 16/4 = 64/4 = ... = 4. Hence, it is a geometric sequence with common ratio 4.

Harmonic Sequence

A harmonic sequence is a sequence obtained by taking the reciprocal of the terms of an arithmetic sequence.

Example: We know that the sequence of natural numbers is an arithmetic sequence. So, taking reciprocals of each term, we get 1, 1/2, 1/3, ..., which is a harmonic sequence as their reciprocals 1, 2, 3, ... form an arithmetic sequence.

Triangular Number Sequence

A triangular number sequence is a sequence that is obtained from a pattern forming equilateral triangles . Look at the figure below.

The sequence 1, 3, 6, 10, and so on is a triangular number sequence.

Square Number Sequence

A square number sequence is a sequence that is obtained from a pattern forming squares . Look at the figure below.

The sequence 1, 4, 9, 16, and so on is a square number sequence.

Cube Number Sequence

A cube number sequence is a sequence that is obtained from a pattern forming cubes . Look at the figure below.

The sequence 1, 8, 27, 64, and so on is a cube number sequence.

Fibonacci Sequence

Fibonacci sequence is a sequence where every term is the sum of the last two preceding terms.

Example: A pair of rabbits do not reproduce in their 1st month. Starting from the 2nd month and every subsequent month, they reproduce another pair. Thus, the number of rabbits starting from 1st month are 0, 1, 1, 2, 3, 4, 7, 11, .... This is called the Fibonacci sequence.

Series and Partial Sums of Sequences

Consider a sequence given by a 1 , a 2 , a 3 , a 4 , .... Then the sum a 1 + a 2 + a 3 + a 4 + .... is the series associated with the sequence. Series can be represented using sigma notation , ∑. So, the series is represented as ∑ n=1 ∞ a n . The partial sum is a part of the series. The sum up to k terms in the series ∑ n=1 k a n and it is called the partial sum of the series. Find more differences between a sequence and a series by clicking here .

Example: Consider a sequence of prime numbers : 2, 3, 5, 7, 11, and so on. The series associated with this is ∑ n=1 ∞ a n , where a n is the n th prime number. The partial sum up to 4 terms is 2+3+5+7=17.

Rules of Sequences

We can generally have two types of rules for a sequence (if it is geometric/arithmetic).

• Implicit rule where a term is expressed in terms of its previous term.
• Explicit rule where any term can be found using a general formula.

Example: Consider the sequence of odd numbers 3, 5, 7, .... We will define two rules to define n th term (general term) of this sequence. Note that this sequence is an arithmetic sequence with the first term 3 (a = 3) and the common difference 2 (d = 5 - 3 = 2). Then:

• Implicit rule: a n = a n-1 + 2
• Explicit rule: a n = a + (n - 1) d = 3 + (n - 1) 2 = 3 + 2n - 2 = 2n + 1.

Here, a n = a + (n - 1) d is the formula for nᵗʰ term of the arithmetic sequence . Let us see more formulas of different types of sequences in the upcoming section.

Sequences Formulas

As we have seen in the previous section, the formula for a sequence is nothing but the formula for its n th term. Let us see the formulas for n th term (a n ) of different types of sequences in math.

• Arithmetic sequence: a n = a + (n - 1) d, where a = the first term and d = common difference.
• Geometric sequence: a n = ar n-1 , where a = the first term and r = common ratio.
• Fibonacci sequence: a n+2 = a n+1 + a n . The first two terms are 0 and 1.
• Square number sequence: a n = n 2 .
• Cube number sequence: a n = n 3 .
• Triangular number sequence: a n = ∑ k=1 n n. This can be further evaluated using the sum of natural numbers formula .

Finding Missing Numbers in a Sequence

Using the above rules/formulas of sequences, we can find the missing numbers of sequences. Sometimes, we don't need to find the general term also to find the missing terms. If the given sequence doesn't belong to any of the specific sequences mentioned above, then we have to observe the pattern of the sequence and define the general term. Using that we can find the missing numbers.

Example: Find the missing number of the sequence 2, 12, 36, 80, __.

It is very clear that the sequence does not belong to any of the sequences that we have mentioned in the previous section. So let us observe the terms. We can see that:

• 2 = 1 2 + 1 3
• 12 = 2 2 + 2 3
• 36 = 3 2 + 3 3
• 80 = 4 2 + 4 3

Thus, the missing number would be 5 2 + 5 3 = 25 + 125 = 150.

Important Notes on Sequences:

• In an arithmetic sequence, each successive term is obtained by adding the common difference to its preceding term.
• In a geometric sequence, each successive term is obtained by multiplying the common ratio to its preceding term.
• The reciprocal of terms in harmonic sequence form an arithmetic sequence.

☛ Related Topics:

• Sequence Calculator
• Arithmetic Sequence Calculator
• Geometric Sequence Calculator
• Series Calculator

Sequences Examples

Example 1: A taxi charges $2 for the first mile and $1.5 for each subsequent mile. How much does Katie need to pay the taxi driver if she travels 20 miles?

The taxi charges for the first few miles are $2, $3.5, $5, ....

This is clearly an arithmetic sequence where the first term is, a = 2 and the common difference is, d = 1.5.

The formula for finding its nth term is,

a n = a + (n - 1) d

Substitute n= 20,

a 20 = 2 + (20 - 1) (1.5) = $30.5.

Answer: Total charges = $30.5.

Example 2: Flora loves growing flowers in her garden. There is 1 flower in the 1 st row, 4 flowers in the 2 nd row, 9 flowers in the 3 rd row, and so on. In which row did she plant 100 flowers?

The sequence of the number of flowers starting from the first row is 1, 4, 9, ....

This is clearly a square number sequence. Its general term is, a n = n 2 .

Substitute a n = 100 here,

Answer: There are 100 flowers in the 10 t h row.

Example 3: The 6 th term and 11 th term of the harmonic sequence are 10 and 18 respectively. Find the common difference between the associated arithmetic sequence .

Let 'a' and 'd' be the first term and the common difference of the arithmetic sequence that is associated with the given harmonic sequence.

By the definition of the harmonic sequence,

6 th term in the associated arithmetic sequence is, a + 5d = 1/10 ... (1)

11 th term in the associated arithmetic sequence is, a + 10d = 1/18 ... (2)

Subtracting (1) from (2),

d = -2/225.

Answer: The required common difference is -2/225.

go to slide go to slide go to slide

Book a Free Trial Class

Practice Questions on Sequences

go to slide go to slide

FAQs on Sequences

What is the definition of sequence.

A sequence is a collection of ordered and indexed items, often numbers arranged according to a certain rule or pattern. In mathematics, sequences are usually represented by a series of terms, each of which corresponds to a particular position or index in the sequence. For example, 3, 7, 11, 15, ... is a sequence as there is a pattern where each term is obtained by adding 4 to its previous term.

What are 4 Types of Sequences?

There are many types of sequences. The following are the 4 important types of sequences:

• Arithmetic sequence
• Geometric sequence
• Harmonic sequence
• Fibonacci sequence

What is the Formula of Sequence?

The general term (or) n th term defines a sequence. If a sequence belongs to specific types like arithmetic, geometric, etc, then we have formulas to find the general term of the respective sequence.

For example, the formula for the n th term of an arithmetic sequence is: a n = a 1 + (n-1)d, where a 1 is the first term, d is the common difference between terms, and a n is the nth term.

Similarly, the formula for the n th term of a geometric sequence is: a n = a 1 * r (n-1) , where a 1 is the first term, r is the common ratio between terms, and a n is the nth term.

What Kind of Sequence is 7, 20, 33, ...?

In the sequence 7, 20, 33, ...,

• second term = 20 = 7 + 13 = first term + 13
• third term = 33 = 20 + 13 = second term + 13

Since every term is obtained by adding 13 to its previous term, it is an arithmetic sequence (which is also known as arithmetic progression ).

How to Construct an Arithmetic Sequence?

Follow the steps mentioned below to construct an arithmetic sequence.

• Take any number as the first term.
• Fix a number as a common difference.
• Add the common difference to the first term to obtain the second term.
• To obtain each successive term, keep adding the common difference to its preceding term.

How to Construct a Geometric Sequence?

Follow the steps mentioned below to construct a geometric sequence.

• Fix a number as a common ratio .
• Multiply the common ratio to the first term to obtain the second term.
• To obtain each successive term, keep multiplying the common ratio to its preceding term.

What is the Difference Between a Sequence and a Series?

A sequence is a collection of elements that are arranged according to a specific pattern whereas a series is the sum of a few or all elements of the sequence. Here are more differences.

How to Find the Sum of Infinite Sequences?

The sum of all infinite sequences may not exist.

• We can find the sum of infinite geometric sequence only when its common ratio (r) is less than 1. If its first term is a, then the sum of its infinite terms is a / (1 - r).
• We can find the sum of an infinite telescoping series by cancelling terms and computing the sum of the rest of the terms.
• To find the sum of a power series, use techniques like differentiation and integration to find a closed-form expression for the sum.

Sequences Practice Questions

Click here for questions, click here for answers, gcse revision cards.

5-a-day Workbooks

Primary Study Cards

Privacy Policy

Terms and Conditions

Corbettmaths © 2012 – 2024

• Mathematicians
• Math Lessons
• Square Roots
• Math Calculators

How to Find the Sum of an Arithmetic Sequence – Easy Steps with Examples

JUMP TO TOPIC

Steps Involved in Finding Sum of An Arithmetic Sequence

Problem solving with arithmetic sequences, practical applications and concept reinforcement.

To find the sum of an arithmetic sequence, I first identify the common difference between consecutive terms. This is because the essential feature of an arithmetic sequence is that each term increases by a steady amount from the one before. With this common difference and knowing the first term, the sequence is completely defined.

If I have the first term, the common difference , and the total number of terms, I can calculate the sum quickly using a simple formula: the sum of the first ( n ) terms $S_n$is given by $S_n = \frac{n}{2} \times (a_1 + a_n$, where $a_1$ is the first term, $a_n$ is the last term, and ( n ) is the number of terms.

Understanding this process is not only practical for solving mathematics problems but also satisfying when I see the sequence culminating in a precise sum. Armed with this knowledge, 

To calculate the sum of an arithmetic sequence , a few simple steps must be followed. These steps use a basic formula that makes finding the sum pretty straightforward.

The sequence begins with a first term (denoted as a ) and each subsequent term increases by a common difference ( d ). To find the sum, you need the first term, the last term of the sequence ( l ), and the number of terms ( n ). Here’s how you can find the sum:

Identify the First and Last Term : I start by determining the first term ( a ) and the last term ( l ). If I don’t have the last term, but I know the number of terms and the common difference, I calculate the last term using $ l = a + (n-1) \times d $.

Determine the Number of Terms : If the number of terms ( n ) is unknown, I find it utilizing the sequence’s pattern or using the information available.

Apply the Formula : I then apply the well-known formula for the sum of an arithmetic series:

$$ S_n = \frac{n}{2} \times (a + l) $$

• $ S_n $ is the sum of the first n terms
• n is the number of terms
• a is the first term
• l is the last term

Let me give you a quick example. If the first term of a sequence ( a ) is 3, the common difference ( d ) is 2, and there are 5 terms ( n ), the sequence is 3, 5, 7, 9, 11. The last term ( l ) is 11. Using the formula:

$$ S_n = \frac{5}{2} \times (3 + 11) = \frac{5}{2} \times 14 = 35 $$

So, the sum of this arithmetic sequence is 35.

Remember, the key is to identify the right terms and apply the formula correctly. Each step is easy to follow, and by doing so, you can quickly find the sum of any arithmetic series .

In working with arithmetic sequences , I often spot the pattern where the difference between consecutive terms is constant. This constant difference, let’s call it d , lets me write down the general form of an arithmetic sequence , which is $a_n = a_1 + (n-1)d$, where:

• $a_n$ is the n -th term of the sequence,
• $a_1$ is the first term, and
• n is the number of terms.

Now, to find the sum of an arithmetic sequence , there’s a handy formula: $S_n = \frac{n}{2} (a_1 + a_n)$. Alternatively, I use $S_n = \frac{n}{2} [2a_1 + (n-1)d]$ if the last term isn’t known or easy to calculate.

Here’s a simplified example to illustrate: Suppose I have an arithmetic sequence starting with $3$, and the common difference d is $5$. I want to find the sum of the first $10$ terms.

• I identify a_1 as $3$, d as $5$, and n as $10$.
• Calculate the 10th term using $a_n = a_1 + (n-1)d$: $a_{10} = 3 + (10-1) \cdot 5 = 48$.
• Use the sum equation (or arithmetic mean): $S_n = \frac{n}{2} (a_1 + a_n)$.
• Plug in the values: $S_{10} = \frac{10}{2} (3 + 48) = 5 \cdot 51 = 255$.

So, the sum of the first $10$ terms is $255$.

If I encounter a sequence with a negative common difference , the process is the same, but the sequence decreases with each term. Let’s say the sequence is $12, 7, 2, \ldots$, and I want the sum of the first $6$ terms:

• a_1 is $12$, d is $-5$, and n is $6$.
• Finding $a_6$: $a_6 = 12 + (6-1)(-5) = 12 – 25 = -13$.
• Calculating $S_n$: $S_6 = \frac{6}{2} (12 – 13) = 3 \cdot (-1) = -3$.

The sum is $-3$, which indicates that the overall value of the terms is negative .

By using the formula correctly and understanding the sequence’s behavior, I can effectively solve for the sum, whether the sequence is increasing or decreasing.

In my experience, arithmetic sequences pop up quite often in real-world scenarios. One common application is in calculating the total number of items over time, such as saving money. Let me guide you through the formula and how it applies to practical situations.

Arithmetic Progression (AP) : This is a sequence of numbers where the difference ( d ) between consecutive terms is constant. For example, if I start saving $100 every month, the series of savings would be an arithmetic progression: $100, $200, $300, …, and so forth.

To find the sum ( S ) of the first n terms of an AP, I use the formula:

$S_n = \frac{n}{2} \times (2a + (n-1)d)$

where a is the first term and n is the number of terms. The average value of each term is simply the sum divided by n . This can also be represented using a recursive formula, where each term is defined in terms of the one before it.

Examples in Time Management : When I calculate the time needed for completing a task that gets progressively quicker due to efficiency, arithmetic sequences are invaluable. If the first task takes 30 minutes and each subsequent task takes 2 minutes less, an AP is formed: 30, 28, 26, … minutes.

Here’s a small table illustrating the savings example over six months:

Using the sum formula for AP, after six months (n=6, a=$100, d=$100), my total savings would be:

$S_6 = \frac{6}{2} \times (2 \times 100 + (6-1) \times 100) = 6 \times (200 + 500) = 6 \times 700 = $4200$

Understanding and applying the formula for the sum of an arithmetic progression is a powerful tool in mathematics and helps to simplify the process of calculating accumulated values over time.

Finding the sum of an arithmetic sequence is a task that involves a blend of observation and application of a straightforward formula. Through my examination of the process, I’ve shared the necessary steps to efficiently sum the terms of any arithmetic sequence . Remember, the formula to calculate the sum of an arithmetic sequence is given by:

$S_n = \frac{n}{2} \times (a_1 + a_n)$

• $S_n $ is the sum of the first n terms,
• $a_1$ is the first term,
• $a_n$ is the nth term,
• and ( n ) is the number of terms.

Or by using the version of the formula that involves the common difference ( d ):

$S_n = \frac{n}{2} \times [2a_1 + (n – 1)d]$

I hope my explanations have illuminated the process, enabling you to tackle problems involving arithmetic sequences with confidence. Whether you’re dealing with textbook exercises or real-world scenarios where series arise, these formulas are your key tools.

With practice, these calculations will become second nature, and you’ll appreciate the rhythm and predictability inherent in arithmetic sequences .

• Pre Calculus
• Probability
• Sets & Set Theory
• Trigonometry

March 12, 2024

The Simplest Math Problem Could Be Unsolvable

The Collatz conjecture has plagued mathematicians for decades—so much so that professors warn their students away from it

By Manon Bischoff

Mathematicians have been hoping for a flash of insight to solve the Collatz conjecture.

James Brey/Getty Images

At first glance, the problem seems ridiculously simple. And yet experts have been searching for a solution in vain for decades. According to mathematician Jeffrey Lagarias, number theorist Shizuo Kakutani told him that during the cold war, “for about a month everybody at Yale [University] worked on it, with no result. A similar phenomenon happened when I mentioned it at the University of Chicago. A joke was made that this problem was part of a conspiracy to slow down mathematical research in the U.S.”

The Collatz conjecture—the vexing puzzle Kakutani described—is one of those supposedly simple problems that people tend to get lost in. For this reason, experienced professors often warn their ambitious students not to get bogged down in it and lose sight of their actual research.

The conjecture itself can be formulated so simply that even primary school students understand it. Take a natural number. If it is odd, multiply it by 3 and add 1; if it is even, divide it by 2. Proceed in the same way with the result x : if x is odd, you calculate 3 x + 1; otherwise calculate x / 2. Repeat these instructions as many times as possible, and, according to the conjecture, you will always end up with the number 1.

On supporting science journalism

If you're enjoying this article, consider supporting our award-winning journalism by subscribing . By purchasing a subscription you are helping to ensure the future of impactful stories about the discoveries and ideas shaping our world today.

For example: If you start with 5, you have to calculate 5 x 3 + 1, which results in 16. Because 16 is an even number, you have to halve it, which gives you 8. Then 8 / 2 = 4, which, when divided by 2, is 2—and 2 / 2 = 1. The process of iterative calculation brings you to the end after five steps.

Of course, you can also continue calculating with 1, which gives you 4, then 2 and then 1 again. The calculation rule leads you into an inescapable loop. Therefore 1 is seen as the end point of the procedure.

Following iterative calculations, you can begin with any of the numbers above and will ultimately reach 1.

Credit: Keenan Pepper/Public domain via Wikimedia Commons

It’s really fun to go through the iterative calculation rule for different numbers and look at the resulting sequences. If you start with 6: 6 → 3 → 10 → 5 → 16 → 8 → 4 → 2 → 1. Or 42: 42 → 21 → 64 → 32 → 16 → 8 → 4 → 2 → 1. No matter which number you start with, you always seem to end up with 1. There are some numbers, such as 27, where it takes quite a long time (27 → 82 → 41 → 124 → 62 → 31 → 94 → 47 → 142 → 71 → 214 → 107 → 322 → 161 → 484 → 242 → 121 → 364 → 182 → 91 → 274 → ...), but so far the result has always been 1. (Admittedly, you have to be patient with the starting number 27, which requires 111 steps.)

But strangely there is still no mathematical proof that the Collatz conjecture is true. And that absence has mystified mathematicians for years.

The origin of the Collatz conjecture is uncertain, which is why this hypothesis is known by many different names. Experts speak of the Syracuse problem, the Ulam problem, the 3 n + 1 conjecture, the Hasse algorithm or the Kakutani problem.

German mathematician Lothar Collatz became interested in iterative functions during his mathematics studies and investigated them. In the early 1930s he also published specialist articles on the subject , but the explicit calculation rule for the problem named after him was not among them. In the 1950s and 1960s the Collatz conjecture finally gained notoriety when mathematicians Helmut Hasse and Shizuo Kakutani, among others, disseminated it to various universities, including Syracuse University.

Like a siren song, this seemingly simple conjecture captivated the experts. For decades they have been looking for proof that after repeating the Collatz procedure a finite number of times, you end up with 1. The reason for this persistence is not just the simplicity of the problem: the Collatz conjecture is related to other important questions in mathematics. For example, such iterative functions appear in dynamic systems, such as models that describe the orbits of planets. The conjecture is also related to the Riemann conjecture, one of the oldest problems in number theory.

Empirical Evidence for the Collatz Conjecture

In 2019 and 2020 researchers checked all numbers below 2 68 , or about 3 x 10 20 numbers in the sequence, in a collaborative computer science project . All numbers in that set fulfill the Collatz conjecture as initial values. But that doesn’t mean that there isn’t an outlier somewhere. There could be a starting value that, after repeated Collatz procedures, yields ever larger values that eventually rise to infinity. This scenario seems unlikely, however, if the problem is examined statistically.

An odd number n is increased to 3 n + 1 after the first step of the iteration, but the result is inevitably even and is therefore halved in the following step. In half of all cases, the halving produces an odd number, which must therefore be increased to 3 n + 1 again, whereupon an even result is obtained again. If the result of the second step is even again, however, you have to divide the new number by 2 twice in every fourth case. In every eighth case, you must divide it by 2 three times, and so on.

In order to evaluate the long-term behavior of this sequence of numbers , Lagarias calculated the geometric mean from these considerations in 1985 and obtained the following result: ( 3 / 2 ) 1/2 x ( 3 ⁄ 4 ) 1/4 x ( 3 ⁄ 8 ) 1/8 · ... = 3 ⁄ 4 . This shows that the sequence elements shrink by an average factor of 3 ⁄ 4 at each step of the iterative calculation rule. It is therefore extremely unlikely that there is a starting value that grows to infinity as a result of the procedure.

There could be a starting value, however, that ends in a loop that is not 4 → 2 → 1. That loop could include significantly more numbers, such that 1 would never be reached.

Such “nontrivial” loops can be found, for example, if you also allow negative integers for the Collatz conjecture: in this case, the iterative calculation rule can end not only at –2 → –1 → –2 → ... but also at –5 → –14 → –7 → –20 → –10 → –5 → ... or –17 → –50 → ... → –17 →.... If we restrict ourselves to natural numbers, no nontrivial loops are known to date—which does not mean that they do not exist. Experts have now been able to show that such a loop in the Collatz problem, however, would have to consist of at least 186 billion numbers .

The length of the Collatz sequences for all numbers from 1 to 9,999 varies greatly.

Credit: Cirne/Public domain via Wikimedia Commons

Even if that sounds unlikely, it doesn’t have to be. In mathematics there are many examples where certain laws only break down after many iterations are considered. For instance,the prime number theorem overestimates the number of primes for only about 10 316 numbers. After that point, the prime number set underestimates the actual number of primes.

Something similar could occur with the Collatz conjecture: perhaps there is a huge number hidden deep in the number line that breaks the pattern observed so far.

A Proof for Almost All Numbers

Mathematicians have been searching for a conclusive proof for decades. The greatest progress was made in 2019 by Fields Medalist Terence Tao of the University of California, Los Angeles, when he proved that almost all starting values of natural numbers eventually end up at a value close to 1.

“Almost all” has a precise mathematical meaning: if you randomly select a natural number as a starting value, it has a 100 percent probability of ending up at 1. ( A zero-probability event, however, is not necessarily an impossible one .) That’s “about as close as one can get to the Collatz conjecture without actually solving it,” Tao said in a talk he gave in 2020 . Unfortunately, Tao’s method cannot generalize to all figures because it is based on statistical considerations.

All other approaches have led to a dead end as well. Perhaps that means the Collatz conjecture is wrong. “Maybe we should be spending more energy looking for counterexamples than we’re currently spending,” said mathematician Alex Kontorovich of Rutgers University in a video on the Veritasium YouTube channel .

Perhaps the Collatz conjecture will be determined true or false in the coming years. But there is another possibility: perhaps it truly is a problem that cannot be proven with available mathematical tools. In fact, in 1987 the late mathematician John Horton Conway investigated a generalization of the Collatz conjecture and found that iterative functions have properties that are unprovable. Perhaps this also applies to the Collatz conjecture. As simple as it may seem, it could be doomed to remain unsolved forever.

This article originally appeared in Spektrum der Wissenschaft and was reproduced with permission.

Can you solve NASA's Pi Day 2024 challenge?

Hungry for Pi? Check out NASA's Pi Day challenge and put your wits to the test solving problems just like NASA scientists and engineers.

Happy Pi Day 2024!

Have you ever wondered what it would be like to solve problems for NASA to help with the exploration of other planets in the solar system ? 

In celebration of Pi Day 2024 , you can do just that and take the annual NASA Pi Day Challenge . This is a fun way to put on your scientist and engineer thinking cap and try your best at a series of questions all surrounding the mathematical constant, pi. 

Related: What is the smallest known planet?

What is pi? If you recall from mathematics class back in grade school, it's approximately 3.14159 and can be used to figure out the circumference of a circle of the volume of a square. 

While there are many uses for it in different STEM jobs and fields, it's also very important for engineers and scientists at NASA to help study not just our planet but others across the solar system and even other galaxies .

This challenge is a tradition that has been on-going for the last decade put on by NASA's Jet Propulsion Laboratory's Education Office and features numerous math problems you have to solve using pi. 

Some of the questions you can answer this year pertain to missions including the Deep Space Optical Communications technology on NASA's Psyche spacecraft , the Double Asteroid Redirection Test (DART) spacecraft, Earth-orbiting satellites, rovers on the Moon, and even the Hubble Space Telescope and James Webb Space Telescope .

—  As scientists find real exoplanets, sci-fi writers change their vision of alien worlds

 — 10 surprising facts about pi

— Pi Day turns 35: The circle of mathematics needs more diversity, advocates say

So, let's get solving! You can find each of the problems with an accompanying worksheet you can do all your work online and the answers will be posted by NASA so you can check your work! 

There are nearly four dozen different questions you can figure out, so try a few or do them all to "cook up" a unique way to get space-y and celebrate Pi Day 2024! 

Join our Space Forums to keep talking space on the latest missions, night sky and more! And if you have a news tip, correction or comment, let us know at: [email protected].

Get the Space.com Newsletter

Breaking space news, the latest updates on rocket launches, skywatching events and more!

Meredith is a regional Murrow award-winning Certified Broadcast Meteorologist and science/space correspondent. She most recently was a Freelance Meteorologist for NY 1 in New York City & the 19 First Alert Weather Team in Cleveland. A self-described "Rocket Girl," Meredith's personal and professional work has drawn recognition over the last decade, including the inaugural Valparaiso University Alumni Association First Decade Achievement Award, two special reports in News 12's Climate Special "Saving Our Shores" that won a Regional Edward R. Murrow Award, multiple Fair Media Council Folio & Press Club of Long Island awards for meteorology & reporting, and a Long Island Business News & NYC TV Week "40 Under 40" Award.

Scientists may have just caught 7 exotic 'ghost particles' as they pierced through Earth

What is the smallest known planet?

India's Chandrayaan-3 lunar lander barely kicked up any moon dust. Here's why that matters

Most Popular

By Meredith Garofalo March 16, 2024

By Elizabeth Howell March 16, 2024

By Keith Cooper March 15, 2024

By Elizabeth Howell March 15, 2024

By Mike Wall March 15, 2024

By Tereza Pultarova March 15, 2024

By Robert Lea March 15, 2024

By Jeff Spry March 15, 2024

By Daisy Dobrijevic March 15, 2024

• 2 The James Webb Space Telescope is digging deep into the mysteries of gas planets
• 3 Sony FE 16-35mm f/2.8 GM II vs Canon RF 15-35mm f/2.8 L IS USM
• 4 Sleeping subduction zone could awaken and form a new 'Ring of Fire' that swallows the Atlantic Ocean
• 5 Lego Creator 3-in-1 Space Astronaut review

Can AI Solve the Math Mysteries Stumping the Field’s Brightest Minds?

Artificial Intelligence already won a gold ribbon in the most elite high school math competition. It could help humans conduct boundary-pushing math research next.

Gear-obsessed editors choose every product we review. We may earn commission if you buy from a link. Why Trust Us?

Each year since 1959, high school math students from more than 100 countries have competed to solve a wide variety of math problems involving algebra , geometry , and number theory quickly and elegantly. Many IMO winners have secured prestigious math awards as adults, including the coveted Fields Medal .

In essence, IMO is a benchmark for students to see if they have what it takes to succeed in the field of mathematics. Now, artificial intelligence has aced the test—well, the geometry part at least.

In a paper published this January in Nature , a team of scientists from Google’s DeepMind have introduced a new AI called AlphaGeometry that’s capable of passing the geometry section of the International Math Olympiad without relying on human examples.

“We’ve made a lot of progress with models like ChatGPT … but when it comes to mathematical problems, these [large language models] essentially score zero,” Thang Luong , Ph.D., a senior staff research scientist at Google DeepMind and a senior author of the AlphaGeometry paper, tells Popular Mechanics . “When you ask [math] questions, the model will give you what looks like an answer, but [it actually] doesn’t make sense.”

For example, things get messy when AI tries to solve an algebraic word problem or a combinatorics problem that asks it to find the number of permutations (or versions) of a number sequence.

To answer math questions of this caliber , AlphaGeometry relies on a combination of symbolic AI—which Luong describes as being precise but slow—and a neural network more similar to large language models (LLMs) that is responsible for the quick, creative side of problem-solving.

Yet, math experts aren’t convinced that an AI made to solve high school-level math problems is ready to take off the training wheels and tackle more difficult subjects, e.g. advanced number theory or combinatorics, let alone boundary-pushing math research.

Why AI Struggles With Math

While LLM-powered AI tools have exploded in the past two years, these models have routinely struggled to handle math problems. This is part of what makes AlphaGeometry stand out from the crowd. But even so, that doesn’t necessarily mean it’s ready to tackle higher-level math yet.

.css-2l0eat{font-family:UnitedSans,UnitedSans-roboto,UnitedSans-local,Helvetica,Arial,Sans-serif;font-size:1.625rem;line-height:1.2;margin:0rem;padding:0.9rem 1rem 1rem;}@media(max-width: 48rem){.css-2l0eat{font-size:1.75rem;line-height:1;}}@media(min-width: 48rem){.css-2l0eat{font-size:1.875rem;line-height:1;}}@media(min-width: 64rem){.css-2l0eat{font-size:2.25rem;line-height:1;}}.css-2l0eat b,.css-2l0eat strong{font-family:inherit;font-weight:bold;}.css-2l0eat em,.css-2l0eat i{font-style:italic;font-family:inherit;} “The challenge of AI is that [it] cannot come up with new concepts.”

Marijin Heule , Ph.D., is an associate professor of computer science at Carnegie Mellon University whose work focuses on another kind of automated theorem prover called SAT solvers. In this case, “SAT” refers to a measure of validity called “satisfiability” and not the math section of the high school SAT.

“When it comes down to solving math problems or problems in general, the challenge of AI is that [it] cannot come up with new concepts,” Heule tells Popular Mechanics .

This limitation impacts symbolic AI and neural networks in different ways, Heule explains, but both stem from the issue that these AI rely on an existing bank of human knowledge. However, this isn’t exactly true for AlphaGeometry because it relies on synthetic data , which isn’t based on human examples but is made to mimic them.

While AIs might not be effective mathematicians on their own, that doesn’t necessarily mean they can’t be great apprentices to human mathematicians.

“At least for the foreseeable future, [AI will] be mostly assisting,” Heule says. “One of the other things that these machines can do really well is they can tell you if there is an incorrect argument and [offer] a counterexample.”

These AI-powered nudges can help researchers distinguish research dead-ends from promising paths.

Why Geometry?

Of all the math fields the AlphaGeometry team could have tackled, Luong says there were a few factors that helped them zero in on geometry .

“I think geometry is visually appealing [and] we do geometry as kids,” he says. “And geometry is everywhere in design and architecture, so it’s very important.”

Geometry also offered a unique challenge as being one of the International Math Olympiad fields with the fewest number of proof examples written in a computer-friendly format (e.g. without pictures).

While Heule agrees that AlphaGeometry is “really cool work,” he admits that designing a geometry solver is one of the easier tasks for a math AI.

While human computer scientists did work behind the scenes to formalize geometry problems in a way that computers can reason about, Heule says the reasoning is pretty straightforward once that preparation work is complete.

In part, this is because the considerations of geometry problems (e.g. the relationship between angles, points, and lines) are fairly contained compared to more complex areas, he says.

Take for example Fermat’s Last Theorem . This number theory problem took over three centuries to solve, and Heule says it would be extremely difficult to explain its solution to AI, let alone ask AI to solve it.

“Large-scale fields of modern mathematics … are so big that any one of them contains multitudes,” says Heather Macbeth , Ph.D., an assistant professor of mathematics at Fordham University with a focus on geometry. “I think, maybe a more precise question would be to talk about the styles of problems, which might occur within any mathematical field that some of these AI systems are useful for,” she tells Popular Mechanics.

For example, AI could be useful for pattern recognition or so-called needle-in-a-haystack problems where mathematicians are looking for something with a very particular property, Macbeth says.

Toward General AI

While AI likely won’t be solving centuries-old math problems in the near future, Luong is confident there are still existing advancements on the horizon for AlphaGeometry and its ilk. Perhaps these models could even graduate high school and take on the Putnam Mathematical Competition for undergraduate students.

But beyond math tests themselves, Luong is hopeful about what models like AlphaGeometry could mean for the field of AI at large—in particular, researchers’ goals of designing a generalized AI.

“If we want to talk about building an artificial general intelligence, where we want the AI to be as smart as a human, I think the AI needs to be able to perform deep reasoning,” Luong says. “This means that the AI needs to be able to plan ahead for many, many steps [and] see the big picture of how things connect together … the IMO is the perfect test for that.”

Sarah is a science and technology journalist based in Boston interested in how innovation and research intersect with our daily lives. She has written for a number of national publications and covers innovation news at Inverse .

.css-cuqpxl:before{padding-right:0.3125rem;content:'//';display:inline;} Pop Mech Pro: Science .css-xtujxj:before{padding-left:0.3125rem;content:'//';display:inline;}

You Can Give Your Body Back to Nature When You Die

How Does UFO Footage Play Tricks on Your Mind?

Why Doesn’t the Living Human Body ‘Go Bad’?

Is the Room-Temperature Superconductor Back?

What 9 Months on a Cruise Ship Can Do to You

Scientists Just Figured Out Why Pee is Yellow

5 Alien Hoaxes That Prove We Truly Want to Believe

Why UFOs Don’t Necessarily Mean Aliens

How Atmospheric Rivers Water Our Planet

Everything You Need to Know About ‘Frostquakes’

Ufology: From Fringe Field to Serious Science