null hypothesis sample proportion

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons
• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

8.4: Hypothesis Test Examples for Proportions

• Last updated
• Save as PDF
• Page ID 11533

• In a hypothesis test problem, you may see words such as "the level of significance is 1%." The "1%" is the preconceived or preset \(\alpha\).
• The statistician setting up the hypothesis test selects the value of α to use before collecting the sample data.
• If no level of significance is given, a common standard to use is \(\alpha = 0.05\).
• When you calculate the \(p\)-value and draw the picture, the \(p\)-value is the area in the left tail, the right tail, or split evenly between the two tails. For this reason, we call the hypothesis test left, right, or two tailed.
• The alternative hypothesis, \(H_{a}\), tells you if the test is left, right, or two-tailed. It is the key to conducting the appropriate test.
• \(H_{a}\) never has a symbol that contains an equal sign.
• Thinking about the meaning of the \(p\)-value: A data analyst (and anyone else) should have more confidence that he made the correct decision to reject the null hypothesis with a smaller \(p\)-value (for example, 0.001 as opposed to 0.04) even if using the 0.05 level for alpha. Similarly, for a large p -value such as 0.4, as opposed to a \(p\)-value of 0.056 (\(\alpha = 0.05\) is less than either number), a data analyst should have more confidence that she made the correct decision in not rejecting the null hypothesis. This makes the data analyst use judgment rather than mindlessly applying rules.

Full Hypothesis Test Examples

Example \(\PageIndex{7}\)

Joon believes that 50% of first-time brides in the United States are younger than their grooms. She performs a hypothesis test to determine if the percentage is the same or different from 50% . Joon samples 100 first-time brides and 53 reply that they are younger than their grooms. For the hypothesis test, she uses a 1% level of significance.

Set up the hypothesis test:

The 1% level of significance means that α = 0.01. This is a test of a single population proportion .

\(H_{0}: p = 0.50\)  \(H_{a}: p \neq 0.50\)

The words "is the same or different from" tell you this is a two-tailed test.

Calculate the distribution needed:

Random variable: \(P′ =\) the percent of of first-time brides who are younger than their grooms.

Distribution for the test: The problem contains no mention of a mean. The information is given in terms of percentages. Use the distribution for P′ , the estimated proportion.

\[P' - N\left(p, \sqrt{\frac{p-q}{n}}\right)\nonumber \]

\[P' - N\left(0.5, \sqrt{\frac{0.5-0.5}{100}}\right)\nonumber \]

where \(p = 0.50, q = 1−p = 0.50\), and \(n = 100\)

Calculate the p -value using the normal distribution for proportions:

\[p\text{-value} = P(p′ < 0.47 or p′ > 0.53) = 0.5485\nonumber \]

where \[x = 53, p' = \frac{x}{n} = \frac{53}{100} = 0.53\nonumber \].

Interpretation of the \(p\text{-value})\: If the null hypothesis is true, there is 0.5485 probability (54.85%) that the sample (estimated) proportion \(p'\) is 0.53 or more OR 0.47 or less (see the graph in Figure).

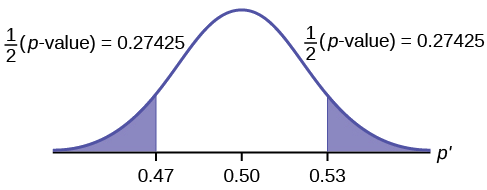
\(\mu = p = 0.50\) comes from \(H_{0}\), the null hypothesis.

\(p′ = 0.53\). Since the curve is symmetrical and the test is two-tailed, the \(p′\) for the left tail is equal to \(0.50 – 0.03 = 0.47\) where \(\mu = p = 0.50\). (0.03 is the difference between 0.53 and 0.50.)

Compare \(\alpha\) and the \(p\text{-value}\):

Since \(\alpha = 0.01\) and \(p\text{-value} = 0.5485\). \(\alpha < p\text{-value}\).

Make a decision: Since \(\alpha < p\text{-value}\), you cannot reject \(H_{0}\).

Conclusion: At the 1% level of significance, the sample data do not show sufficient evidence that the percentage of first-time brides who are younger than their grooms is different from 50%.

The \(p\text{-value}\) can easily be calculated.

Press STAT and arrow over to TESTS . Press 5:1-PropZTest . Enter .5 for \(p_{0}\), 53 for \(x\) and 100 for \(n\). Arrow down to Prop and arrow to not equals \(p_{0}\). Press ENTER . Arrow down to Calculate and press ENTER . The calculator calculates the \(p\text{-value}\) (\(p = 0.5485\)) and the test statistic (\(z\)-score). Prop not equals .5 is the alternate hypothesis. Do this set of instructions again except arrow to Draw (instead of Calculate ). Press ENTER . A shaded graph appears with \(\(z\) = 0.6\) (test statistic) and \(p = 0.5485\) (\(p\text{-value}\)). Make sure when you use Draw that no other equations are highlighted in \(Y =\) and the plots are turned off.

The Type I and Type II errors are as follows:

The Type I error is to conclude that the proportion of first-time brides who are younger than their grooms is different from 50% when, in fact, the proportion is actually 50%. (Reject the null hypothesis when the null hypothesis is true).

The Type II error is there is not enough evidence to conclude that the proportion of first time brides who are younger than their grooms differs from 50% when, in fact, the proportion does differ from 50%. (Do not reject the null hypothesis when the null hypothesis is false.)

Exercise \(\PageIndex{7}\)

A teacher believes that 85% of students in the class will want to go on a field trip to the local zoo. She performs a hypothesis test to determine if the percentage is the same or different from 85%. The teacher samples 50 students and 39 reply that they would want to go to the zoo. For the hypothesis test, use a 1% level of significance.

First, determine what type of test this is, set up the hypothesis test, find the \(p\text{-value}\), sketch the graph, and state your conclusion.

Since the problem is about percentages, this is a test of single population proportions.

• \(H_{0} : p = 0.85\)
• \(H_{a}: p \neq 0.85\)
• \(p = 0.7554\)

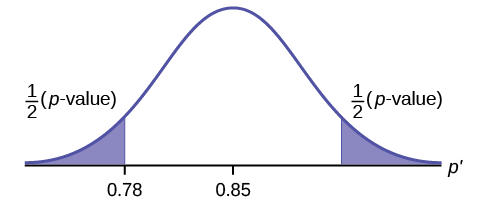
Because \(p > \alpha\), we fail to reject the null hypothesis. There is not sufficient evidence to suggest that the proportion of students that want to go to the zoo is not 85%.

Example \(\PageIndex{8}\)

Suppose a consumer group suspects that the proportion of households that have three cell phones is 30%. A cell phone company has reason to believe that the proportion is not 30%. Before they start a big advertising campaign, they conduct a hypothesis test. Their marketing people survey 150 households with the result that 43 of the households have three cell phones.

Set up the Hypothesis Test:

\(H_{0}: p = 0.30, H_{a}: p \neq 0.30\)

Determine the distribution needed:

The random variable is \(P′ =\) proportion of households that have three cell phones.

The distribution for the hypothesis test is \(P' - N\left(0.30, \sqrt{\frac{(0.30 \cdot 0.70)}{150}}\right)\)

Exercise 9.6.8.2

a. The value that helps determine the \(p\text{-value}\) is \(p′\). Calculate \(p′\).

a. \(p' = \frac{x}{n}\) where \(x\) is the number of successes and \(n\) is the total number in the sample.

\(x = 43, n = 150\)

\(p′ = 43150\)

Exercise 9.6.8.3

b. What is a success for this problem?

b. A success is having three cell phones in a household.

Exercise 9.6.8.4

c. What is the level of significance?

c. The level of significance is the preset \(\alpha\). Since \(\alpha\) is not given, assume that \(\alpha = 0.05\).

Exercise 9.6.8.5

d. Draw the graph for this problem. Draw the horizontal axis. Label and shade appropriately.

Calculate the \(p\text{-value}\).

d. \(p\text{-value} = 0.7216\)

Exercise 9.6.8.6

e. Make a decision. _____________(Reject/Do not reject) \(H_{0}\) because____________.

e. Assuming that \(\alpha = 0.05, \alpha < p\text{-value}\). The decision is do not reject \(H_{0}\) because there is not sufficient evidence to conclude that the proportion of households that have three cell phones is not 30%.

Exercise \(\PageIndex{8}\)

Marketers believe that 92% of adults in the United States own a cell phone. A cell phone manufacturer believes that number is actually lower. 200 American adults are surveyed, of which, 174 report having cell phones. Use a 5% level of significance. State the null and alternative hypothesis, find the p -value, state your conclusion, and identify the Type I and Type II errors.

• \(H_{0}: p = 0.92\)
• \(H_{a}: p < 0.92\)
• \(p\text{-value} = 0.0046\)

Because \(p < 0.05\), we reject the null hypothesis. There is sufficient evidence to conclude that fewer than 92% of American adults own cell phones.

• Type I Error: To conclude that fewer than 92% of American adults own cell phones when, in fact, 92% of American adults do own cell phones (reject the null hypothesis when the null hypothesis is true).
• Type II Error: To conclude that 92% of American adults own cell phones when, in fact, fewer than 92% of American adults own cell phones (do not reject the null hypothesis when the null hypothesis is false).

The next example is a poem written by a statistics student named Nicole Hart. The solution to the problem follows the poem. Notice that the hypothesis test is for a single population proportion. This means that the null and alternate hypotheses use the parameter \(p\). The distribution for the test is normal. The estimated proportion \(p′\) is the proportion of fleas killed to the total fleas found on Fido. This is sample information. The problem gives a preconceived \(\alpha = 0.01\), for comparison, and a 95% confidence interval computation. The poem is clever and humorous, so please enjoy it!

Example \(\PageIndex{9}\)

My dog has so many fleas,

They do not come off with ease. As for shampoo, I have tried many types Even one called Bubble Hype, Which only killed 25% of the fleas, Unfortunately I was not pleased.

I've used all kinds of soap, Until I had given up hope Until one day I saw An ad that put me in awe.

A shampoo used for dogs Called GOOD ENOUGH to Clean a Hog Guaranteed to kill more fleas.

I gave Fido a bath And after doing the math His number of fleas Started dropping by 3's! Before his shampoo I counted 42.

At the end of his bath, I redid the math And the new shampoo had killed 17 fleas. So now I was pleased.

Now it is time for you to have some fun With the level of significance being .01, You must help me figure out

Use the new shampoo or go without?

\(H_{0}: p \leq 0.25\)   \(H_{a}: p > 0.25\)

In words, CLEARLY state what your random variable \(\bar{X}\) or \(P′\) represents.

\(P′ =\) The proportion of fleas that are killed by the new shampoo

State the distribution to use for the test.

\[N\left(0.25, \sqrt{\frac{(0.25){1-0.25}}{42}}\right)\nonumber \]

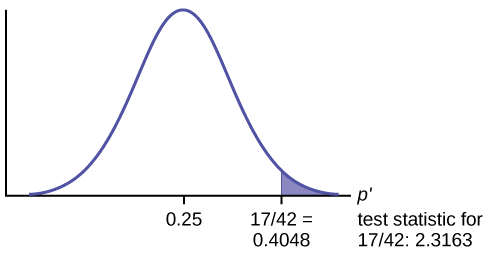
Test Statistic: \(z = 2.3163\)

Calculate the \(p\text{-value}\) using the normal distribution for proportions:

\[p\text{-value} = 0.0103\nonumber \]

In one to two complete sentences, explain what the p -value means for this problem.

If the null hypothesis is true (the proportion is 0.25), then there is a 0.0103 probability that the sample (estimated) proportion is 0.4048 \(\left(\frac{17}{42}\right)\) or more.

Use the previous information to sketch a picture of this situation. CLEARLY, label and scale the horizontal axis and shade the region(s) corresponding to the \(p\text{-value}\).

Indicate the correct decision (“reject” or “do not reject” the null hypothesis), the reason for it, and write an appropriate conclusion, using complete sentences.

Conclusion: At the 1% level of significance, the sample data do not show sufficient evidence that the percentage of fleas that are killed by the new shampoo is more than 25%.

Construct a 95% confidence interval for the true mean or proportion. Include a sketch of the graph of the situation. Label the point estimate and the lower and upper bounds of the confidence interval.

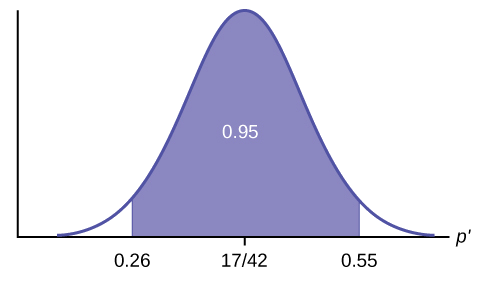
Confidence Interval: (0.26,0.55) We are 95% confident that the true population proportion p of fleas that are killed by the new shampoo is between 26% and 55%.

This test result is not very definitive since the \(p\text{-value}\) is very close to alpha. In reality, one would probably do more tests by giving the dog another bath after the fleas have had a chance to return.

Example \(\PageIndex{11}\)

In a study of 420,019 cell phone users, 172 of the subjects developed brain cancer. Test the claim that cell phone users developed brain cancer at a greater rate than that for non-cell phone users (the rate of brain cancer for non-cell phone users is 0.0340%). Since this is a critical issue, use a 0.005 significance level. Explain why the significance level should be so low in terms of a Type I error.

We will follow the four-step process.

• \(H_{0}: p \leq 0.00034\)
• \(H_{a}: p > 0.00034\)

If we commit a Type I error, we are essentially accepting a false claim. Since the claim describes cancer-causing environments, we want to minimize the chances of incorrectly identifying causes of cancer.

• We will be testing a sample proportion with \(x = 172\) and \(n = 420,019\). The sample is sufficiently large because we have \(np = 420,019(0.00034) = 142.8\), \(nq = 420,019(0.99966) = 419,876.2\), two independent outcomes, and a fixed probability of success \(p = 0.00034\). Thus we will be able to generalize our results to the population.

Figure 9.6.11.

Figure 9.6.12.

• Since the \(p\text{-value} = 0.0073\) is greater than our alpha value \(= 0.005\), we cannot reject the null. Therefore, we conclude that there is not enough evidence to support the claim of higher brain cancer rates for the cell phone users.

Example \(\PageIndex{12}\)

According to the US Census there are approximately 268,608,618 residents aged 12 and older. Statistics from the Rape, Abuse, and Incest National Network indicate that, on average, 207,754 rapes occur each year (male and female) for persons aged 12 and older. This translates into a percentage of sexual assaults of 0.078%. In Daviess County, KY, there were reported 11 rapes for a population of 37,937. Conduct an appropriate hypothesis test to determine if there is a statistically significant difference between the local sexual assault percentage and the national sexual assault percentage. Use a significance level of 0.01.

We will follow the four-step plan.

• We need to test whether the proportion of sexual assaults in Daviess County, KY is significantly different from the national average.
• \(H_{0}: p = 0.00078\)
• \(H_{a}: p \neq 0.00078\)

Figure 9.6.13.

Figure 9.6.14.

• Since the \(p\text{-value}\), \(p = 0.00063\), is less than the alpha level of 0.01, the sample data indicates that we should reject the null hypothesis. In conclusion, the sample data support the claim that the proportion of sexual assaults in Daviess County, Kentucky is different from the national average proportion.

The hypothesis test itself has an established process. This can be summarized as follows:

• Determine \(H_{0}\) and \(H_{a}\). Remember, they are contradictory.
• Determine the random variable.
• Determine the distribution for the test.
• Draw a graph, calculate the test statistic, and use the test statistic to calculate the \(p\text{-value}\). (A z -score and a t -score are examples of test statistics.)
• Compare the preconceived α with the p -value, make a decision (reject or do not reject H 0 ), and write a clear conclusion using English sentences.

Notice that in performing the hypothesis test, you use \(\alpha\) and not \(\beta\). \(\beta\) is needed to help determine the sample size of the data that is used in calculating the \(p\text{-value}\). Remember that the quantity \(1 – \beta\) is called the Power of the Test . A high power is desirable. If the power is too low, statisticians typically increase the sample size while keeping α the same.If the power is low, the null hypothesis might not be rejected when it should be.

• Data from Amit Schitai. Director of Instructional Technology and Distance Learning. LBCC.
• Data from Bloomberg Businessweek . Available online at http://www.businessweek.com/news/2011- 09-15/nyc-smoking-rate-falls-to-record-low-of-14-bloomberg-says.html.
• Data from energy.gov. Available online at http://energy.gov (accessed June 27. 2013).
• Data from Gallup®. Available online at www.gallup.com (accessed June 27, 2013).
• Data from Growing by Degrees by Allen and Seaman.
• Data from La Leche League International. Available online at www.lalecheleague.org/Law/BAFeb01.html.
• Data from the American Automobile Association. Available online at www.aaa.com (accessed June 27, 2013).
• Data from the American Library Association. Available online at www.ala.org (accessed June 27, 2013).
• Data from the Bureau of Labor Statistics. Available online at http://www.bls.gov/oes/current/oes291111.htm .
• Data from the Centers for Disease Control and Prevention. Available online at www.cdc.gov (accessed June 27, 2013)
• Data from the U.S. Census Bureau, available online at quickfacts.census.gov/qfd/states/00000.html (accessed June 27, 2013).
• Data from the United States Census Bureau. Available online at www.census.gov/hhes/socdemo/language/.
• Data from Toastmasters International. Available online at http://toastmasters.org/artisan/deta...eID=429&Page=1 .
• Data from Weather Underground. Available online at www.wunderground.com (accessed June 27, 2013).
• Federal Bureau of Investigations. “Uniform Crime Reports and Index of Crime in Daviess in the State of Kentucky enforced by Daviess County from 1985 to 2005.” Available online at http://www.disastercenter.com/kentucky/crime/3868.htm (accessed June 27, 2013).
• “Foothill-De Anza Community College District.” De Anza College, Winter 2006. Available online at research.fhda.edu/factbook/DA...t_da_2006w.pdf.
• Johansen, C., J. Boice, Jr., J. McLaughlin, J. Olsen. “Cellular Telephones and Cancer—a Nationwide Cohort Study in Denmark.” Institute of Cancer Epidemiology and the Danish Cancer Society, 93(3):203-7. Available online at http://www.ncbi.nlm.nih.gov/pubmed/11158188 (accessed June 27, 2013).
• Rape, Abuse & Incest National Network. “How often does sexual assault occur?” RAINN, 2009. Available online at www.rainn.org/get-information...sexual-assault (accessed June 27, 2013).

Contributors and Attributions

Barbara Illowsky and Susan Dean (De Anza College) with many other contributing authors. Content produced by OpenStax College is licensed under a Creative Commons Attribution License 4.0 license. Download for free at http://cnx.org/contents/[email protected] .

9.1 Null and Alternative Hypotheses

The actual test begins by considering two hypotheses . They are called the null hypothesis and the alternative hypothesis . These hypotheses contain opposing viewpoints.

H 0 , the — null hypothesis: a statement of no difference between sample means or proportions or no difference between a sample mean or proportion and a population mean or proportion. In other words, the difference equals 0.

H a —, the alternative hypothesis: a claim about the population that is contradictory to H 0 and what we conclude when we reject H 0 .

Since the null and alternative hypotheses are contradictory, you must examine evidence to decide if you have enough evidence to reject the null hypothesis or not. The evidence is in the form of sample data.

After you have determined which hypothesis the sample supports, you make a decision. There are two options for a decision. They are reject H 0 if the sample information favors the alternative hypothesis or do not reject H 0 or decline to reject H 0 if the sample information is insufficient to reject the null hypothesis.

Mathematical Symbols Used in H 0 and H a :

H 0 always has a symbol with an equal in it. H a never has a symbol with an equal in it. The choice of symbol depends on the wording of the hypothesis test. However, be aware that many researchers use = in the null hypothesis, even with > or < as the symbol in the alternative hypothesis. This practice is acceptable because we only make the decision to reject or not reject the null hypothesis.

Example 9.1

H 0 : No more than 30 percent of the registered voters in Santa Clara County voted in the primary election. p ≤ 30 H a : More than 30 percent of the registered voters in Santa Clara County voted in the primary election. p > 30

A medical trial is conducted to test whether or not a new medicine reduces cholesterol by 25 percent. State the null and alternative hypotheses.

Example 9.2

We want to test whether the mean GPA of students in American colleges is different from 2.0 (out of 4.0). The null and alternative hypotheses are the following: H 0 : μ = 2.0 H a : μ ≠ 2.0

We want to test whether the mean height of eighth graders is 66 inches. State the null and alternative hypotheses. Fill in the correct symbol (=, ≠, ≥, <, ≤, >) for the null and alternative hypotheses.

• H 0 : μ __ 66
• H a : μ __ 66

Example 9.3

We want to test if college students take fewer than five years to graduate from college, on the average. The null and alternative hypotheses are the following: H 0 : μ ≥ 5 H a : μ < 5

We want to test if it takes fewer than 45 minutes to teach a lesson plan. State the null and alternative hypotheses. Fill in the correct symbol ( =, ≠, ≥, <, ≤, >) for the null and alternative hypotheses.

• H 0 : μ __ 45
• H a : μ __ 45

Example 9.4

An article on school standards stated that about half of all students in France, Germany, and Israel take advanced placement exams and a third of the students pass. The same article stated that 6.6 percent of U.S. students take advanced placement exams and 4.4 percent pass. Test if the percentage of U.S. students who take advanced placement exams is more than 6.6 percent. State the null and alternative hypotheses. H 0 : p ≤ 0.066 H a : p > 0.066

On a state driver’s test, about 40 percent pass the test on the first try. We want to test if more than 40 percent pass on the first try. Fill in the correct symbol (=, ≠, ≥, <, ≤, >) for the null and alternative hypotheses.

• H 0 : p __ 0.40
• H a : p __ 0.40

Collaborative Exercise

Bring to class a newspaper, some news magazines, and some internet articles. In groups, find articles from which your group can write null and alternative hypotheses. Discuss your hypotheses with the rest of the class.

As an Amazon Associate we earn from qualifying purchases.

This book may not be used in the training of large language models or otherwise be ingested into large language models or generative AI offerings without OpenStax's permission.

Want to cite, share, or modify this book? This book uses the Creative Commons Attribution License and you must attribute Texas Education Agency (TEA). The original material is available at: https://www.texasgateway.org/book/tea-statistics . Changes were made to the original material, including updates to art, structure, and other content updates.

Access for free at https://openstax.org/books/statistics/pages/1-introduction

• Authors: Barbara Illowsky, Susan Dean
• Publisher/website: OpenStax
• Book title: Statistics
• Publication date: Mar 27, 2020
• Location: Houston, Texas
• Book URL: https://openstax.org/books/statistics/pages/1-introduction
• Section URL: https://openstax.org/books/statistics/pages/9-1-null-and-alternative-hypotheses

© Jan 23, 2024 Texas Education Agency (TEA). The OpenStax name, OpenStax logo, OpenStax book covers, OpenStax CNX name, and OpenStax CNX logo are not subject to the Creative Commons license and may not be reproduced without the prior and express written consent of Rice University.

Have a language expert improve your writing

Run a free plagiarism check in 10 minutes, generate accurate citations for free.

• Knowledge Base
• Null and Alternative Hypotheses | Definitions & Examples

Null & Alternative Hypotheses | Definitions, Templates & Examples

Published on May 6, 2022 by Shaun Turney . Revised on June 22, 2023.

The null and alternative hypotheses are two competing claims that researchers weigh evidence for and against using a statistical test :

• Null hypothesis ( H 0 ): There’s no effect in the population .
• Alternative hypothesis ( H a or H 1 ) : There’s an effect in the population.

Table of contents

Answering your research question with hypotheses, what is a null hypothesis, what is an alternative hypothesis, similarities and differences between null and alternative hypotheses, how to write null and alternative hypotheses, other interesting articles, frequently asked questions.

The null and alternative hypotheses offer competing answers to your research question . When the research question asks “Does the independent variable affect the dependent variable?”:

• The null hypothesis ( H 0 ) answers “No, there’s no effect in the population.”
• The alternative hypothesis ( H a ) answers “Yes, there is an effect in the population.”

The null and alternative are always claims about the population. That’s because the goal of hypothesis testing is to make inferences about a population based on a sample . Often, we infer whether there’s an effect in the population by looking at differences between groups or relationships between variables in the sample. It’s critical for your research to write strong hypotheses .

You can use a statistical test to decide whether the evidence favors the null or alternative hypothesis. Each type of statistical test comes with a specific way of phrasing the null and alternative hypothesis. However, the hypotheses can also be phrased in a general way that applies to any test.

Receive feedback on language, structure, and formatting

Professional editors proofread and edit your paper by focusing on:

• Academic style
• Vague sentences
• Style consistency

See an example

The null hypothesis is the claim that there’s no effect in the population.

If the sample provides enough evidence against the claim that there’s no effect in the population ( p ≤ α), then we can reject the null hypothesis . Otherwise, we fail to reject the null hypothesis.

Although “fail to reject” may sound awkward, it’s the only wording that statisticians accept . Be careful not to say you “prove” or “accept” the null hypothesis.

Null hypotheses often include phrases such as “no effect,” “no difference,” or “no relationship.” When written in mathematical terms, they always include an equality (usually =, but sometimes ≥ or ≤).

You can never know with complete certainty whether there is an effect in the population. Some percentage of the time, your inference about the population will be incorrect. When you incorrectly reject the null hypothesis, it’s called a type I error . When you incorrectly fail to reject it, it’s a type II error.

Examples of null hypotheses

The table below gives examples of research questions and null hypotheses. There’s always more than one way to answer a research question, but these null hypotheses can help you get started.

*Note that some researchers prefer to always write the null hypothesis in terms of “no effect” and “=”. It would be fine to say that daily meditation has no effect on the incidence of depression and p 1 = p 2 .

The alternative hypothesis ( H a ) is the other answer to your research question . It claims that there’s an effect in the population.

Often, your alternative hypothesis is the same as your research hypothesis. In other words, it’s the claim that you expect or hope will be true.

The alternative hypothesis is the complement to the null hypothesis. Null and alternative hypotheses are exhaustive, meaning that together they cover every possible outcome. They are also mutually exclusive, meaning that only one can be true at a time.

Alternative hypotheses often include phrases such as “an effect,” “a difference,” or “a relationship.” When alternative hypotheses are written in mathematical terms, they always include an inequality (usually ≠, but sometimes < or >). As with null hypotheses, there are many acceptable ways to phrase an alternative hypothesis.

Examples of alternative hypotheses

The table below gives examples of research questions and alternative hypotheses to help you get started with formulating your own.

Null and alternative hypotheses are similar in some ways:

• They’re both answers to the research question.
• They both make claims about the population.
• They’re both evaluated by statistical tests.

However, there are important differences between the two types of hypotheses, summarized in the following table.

Prevent plagiarism. Run a free check.

To help you write your hypotheses, you can use the template sentences below. If you know which statistical test you’re going to use, you can use the test-specific template sentences. Otherwise, you can use the general template sentences.

General template sentences

The only thing you need to know to use these general template sentences are your dependent and independent variables. To write your research question, null hypothesis, and alternative hypothesis, fill in the following sentences with your variables:

Does independent variable affect dependent variable ?

• Null hypothesis ( H 0 ): Independent variable does not affect dependent variable.
• Alternative hypothesis ( H a ): Independent variable affects dependent variable.

Test-specific template sentences

Once you know the statistical test you’ll be using, you can write your hypotheses in a more precise and mathematical way specific to the test you chose. The table below provides template sentences for common statistical tests.

Note: The template sentences above assume that you’re performing one-tailed tests . One-tailed tests are appropriate for most studies.

If you want to know more about statistics , methodology , or research bias , make sure to check out some of our other articles with explanations and examples.

• Normal distribution
• Descriptive statistics
• Measures of central tendency
• Correlation coefficient

Methodology

• Cluster sampling
• Stratified sampling
• Types of interviews
• Cohort study
• Thematic analysis

Research bias

• Implicit bias
• Cognitive bias
• Survivorship bias
• Availability heuristic
• Nonresponse bias
• Regression to the mean

Hypothesis testing is a formal procedure for investigating our ideas about the world using statistics. It is used by scientists to test specific predictions, called hypotheses , by calculating how likely it is that a pattern or relationship between variables could have arisen by chance.

Null and alternative hypotheses are used in statistical hypothesis testing . The null hypothesis of a test always predicts no effect or no relationship between variables, while the alternative hypothesis states your research prediction of an effect or relationship.

The null hypothesis is often abbreviated as H 0 . When the null hypothesis is written using mathematical symbols, it always includes an equality symbol (usually =, but sometimes ≥ or ≤).

The alternative hypothesis is often abbreviated as H a or H 1 . When the alternative hypothesis is written using mathematical symbols, it always includes an inequality symbol (usually ≠, but sometimes < or >).

A research hypothesis is your proposed answer to your research question. The research hypothesis usually includes an explanation (“ x affects y because …”).

A statistical hypothesis, on the other hand, is a mathematical statement about a population parameter. Statistical hypotheses always come in pairs: the null and alternative hypotheses . In a well-designed study , the statistical hypotheses correspond logically to the research hypothesis.

Cite this Scribbr article

If you want to cite this source, you can copy and paste the citation or click the “Cite this Scribbr article” button to automatically add the citation to our free Citation Generator.

Turney, S. (2023, June 22). Null & Alternative Hypotheses | Definitions, Templates & Examples. Scribbr. Retrieved April 9, 2024, from https://www.scribbr.com/statistics/null-and-alternative-hypotheses/

Is this article helpful?

Shaun Turney

Other students also liked, inferential statistics | an easy introduction & examples, hypothesis testing | a step-by-step guide with easy examples, type i & type ii errors | differences, examples, visualizations, what is your plagiarism score.

Chapter 8: Inference for One Proportion

Hypothesis test for a population proportion (3 of 3), learning objectives.

• Conduct a hypothesis test for a population proportion. State a conclusion in context.
• Interpret the P-value as a conditional probability in the context of a hypothesis test about a population proportion.
• Distinguish statistical significance from practical importance.
• From a description of a study, evaluate whether the conclusion of a hypothesis test is reasonable.

More about the P-Value

The P-value is a probability that describes the likelihood of the data if the null hypothesis is true. More specifically, the P-value is the probability that sample results are as extreme as or more extreme than the data if the null hypothesis is true. The phrase “as extreme as or more extreme than” means farther from the center of the sampling distribution in the direction of the alternative hypothesis.

More generally, we view the P-value a description of the strength of the evidence against the null hypothesis and in support of the alternative hypothesis. But the P-value is a probability about sample results, not about the null or alternative hypothesis.

One More Note about P-Values and the Significance Level

You may wonder why 5% is often selected as the significance level in hypothesis testing and why 1% is also a commonly used level. It is largely due to just convenience and tradition. When Ronald Fisher (one of the founders of modern statistics) published one of his tables, he used a mathematically convenient scale that included 5% and 1%. Later, these same 5% and 1% levels were used by other people, in part just because Fisher was so highly esteemed. But mostly, these are arbitrary levels.

The idea of selecting some sort of relatively small cutoff was historically important in the development of statistics. But it’s important to remember that there is really a continuous range of increasing confidence toward the alternative hypothesis, not a single all-or-nothing value. There isn’t much meaningful difference, for instance, between the P-values 0.049 and 0.051, and it would be foolish to declare one case definitely a “real” effect and the other case definitely a “random” effect. In either case, the study results are roughly 5% likely by chance if there’s no actual effect.

Whether such a P-value is sufficient for us to reject a particular null hypothesis ultimately depends on the risk of making the wrong decision and the extent to which the hypothesized effect might contradict our prior experience or previous studies.

Sample Size and Hypothesis Testing

Consider our earlier example about teenagers and Internet access. According to the Kaiser Family Foundation, 84% of U.S. children ages 8 to 18 had Internet access at home as of August 2009. Researchers wonder if this number has changed since then. The hypotheses we tested were:

• H 0 : p = 0.84
• H a : p ≠ 0.84

The original sample consisted of 500 children, and 86% of them had Internet access at home. The P-value was about 0.22, which was not strong enough to reject the null hypothesis. There was not enough evidence to show that the proportion of all U.S. children ages 8 to 18 have Internet access at home.

Suppose we sampled 2,000 children and the sample proportion was still 86%. Our test statistic would be Z ≈ 2.44, and our P-value would be about 0.015. The larger sample size would allow us to reject the null hypothesis even though the sample proportion was the same.

Why does this happen? Larger samples vary less, so a sample proportion of 0.86 is more unusual with larger samples than with smaller samples if the population proportion is really 0.84. This means that if the alternative hypothesis is true, a larger sample size will make it more likely that we reject the null. Therefore, we generally prefer a larger sample as we have seen previously.

Drawing Conclusions from Hypothesis Tests

It is tempting to get involved in the details of a hypothesis test without thinking about how the data was collected. Whether we are calculating a confidence interval or performing a hypothesis test, the results are meaningless without a properly designed study. Consider the following exercises about how data collection can affect the results of a study.

Learn By Doing

Let’s summarize.

In this section, we looked at the four steps of a hypothesis test as they relate to a claim about a population proportion.

Step 1: Determine the hypotheses.

• The hypotheses are claims about the population proportion, p .
• The null hypothesis is a hypothesis that the proportion equals a specific value, p 0 .
• The alternative hypothesis is the competing claim that the parameter is less than, greater than, or not equal to p 0 .

Step 2: Collect the data.

Since the hypothesis test is based on probability, random selection or assignment is essential in data production. Additionally, we need to check whether the sample proportion can be np ≥ 10 and n (1 − p ) ≥ 10.

Step 3: Assess the evidence.

• Determine the test statistic which is the z -score for the sample proportion. The formula is: [latex]Z=\frac{\stackrel{ˆ}{p}-{p}_{0}}{\sqrt{\frac{{p}_{0}(1-{p}_{0})}{n}}}[/latex]
• Use the test statistic, together with the alternative hypothesis to determine the P-value. You can use a standard normal table (or Z -table) or technology (such as the simulations on the second page of this topic) to find the P-value.
• If the alternative hypothesis is greater than, the P-value is the area to the right of the test statistic. If the alternative hypothesis is less than, the P-value is the area to the left of the test statistic. If the alternative hypothesis is not equal to, the P-value is equal to double the tail area beyond the test statistic.

Step 4: Give the conclusion.

• A small P-value says the data is unlikely to occur if the null is true. If the P-value is less than or equal to the significance level, we reject the null hypothesis and accept the alternative hypothesis instead.
• If the P-value is greater than the significance level, we say we “fail to reject” the null hypothesis. We never say that we “accept” the null hypothesis. We just say that we don’t have enough evidence to reject it. This is equivalent to saying we don’t have enough evidence to support the alternative hypothesis.
• We write the conclusion in the context of the research question. Our conclusion is usually a statement about the alternative hypothesis (we accept H a or fail to accept H a ) and should include the P-value.

Other Hypothesis Testing Notes

Remember that the P-value is the probability of seeing a sample proportion as extreme as the one observed from the data if the null hypothesis is true. The probability is about the random sample, not about the null or alternative hypothesis.

A larger sample size makes it more likely that we will reject the null hypothesis if the alternative is true. Another way of thinking about this is that increasing the sample size will decrease the likelihood of a type II error. Recall that a type II error is failing to reject the null hypothesis when the alternative is true.

Increasing the sample size can have the unintended effect of making the test sensitive to differences so small they don’t matter. A statistically significant difference is one large enough that it is unlikely to be due to sampling variability alone. Even a difference so small that it is not important can be statistically significant if the sample size is big enough.

Finally, remember the phrase “garbage in, garbage out.” If the data collection methods are poor, then the results of a hypothesis test are meaningless. No statistical methods can create useful information if our data comes from convenience or voluntary response samples. Additionally, the results of a hypothesis test apply only to the population from whom the sample was chosen.

• Concepts in Statistics. Provided by : Open Learning Initiative. Located at : http://oli.cmu.edu . License : CC BY: Attribution

Privacy Policy

Teach yourself statistics

Hypothesis Test of a Proportion (Small Sample)

This lesson explains how to test a hypothesis about a proportion when a simple random sample has fewer than 10 successes or 10 failures - a situation that often occurs with small samples. (In a previous lesson , we showed how to conduct a hypothesis test for a proportion when a simple random sample includes at least 10 successes and 10 failures.)

The approach described in this lesson is appropriate, as long as the sample includes at least one success and one failure. The key steps are:

• Formulate the hypotheses to be tested. This means stating the null hypothesis and the alternative hypothesis .
• Determine the sampling distribution of the proportion. If the sample proportion is the outcome of a binomial experiment , the sampling distribution will be binomial. If it is the outcome of a hypergeometric experiment , the sampling distribution will be hypergeometric.
• Specify the significance level . (Researchers often set the significance level equal to 0.05 or 0.01, although other values may be used.)
• Based on the hypotheses, the sampling distribution, and the significance level, define the region of acceptance .
• Test the null hypothesis. If the sample proportion falls within the region of acceptance, do not reject the null hypothesis; otherwise, reject the null hypothesis.

The following examples illustrate how to test hypotheses with small samples. The first example involves a binomial experiment; and the second example, a hypergeometric experiment.

Example 1: Sampling With Replacement

Suppose an urn contains 30 marbles. Some marbles are red, and the rest are green. A researcher hypothesizes that the urn contains 15 or more red marbles. The researcher randomly samples five marbles, with replacement , from the urn. Two of the selected marbles are red, and three are green. Based on the sample results, should the researcher reject the null hypothesis? Use a significance level of 0.20.

Solution: There are five steps in conducting a hypothesis test, as described in the previous section. We work through each of the five steps below:

Null hypothesis: P >= 0.50

Alternative hypothesis: P < 0.50

Given those inputs (a binomial distribution where the true population proportion is equal to 0.50), the sampling distribution of the proportion can be determined. It appears in the table below, which shows individual probabilities for single events and cumulative probabilities for multiple events. (Elsewhere on this website, we showed how to compute binomial probabilities that form the body of the table.)

• Specify significance level . The significance level was set at 0.20. (This means that the probability of making a Type I error is 0.20, assuming that the null hypothesis is true.)

However, we can define a region of acceptance for which the significance level would be no more than 0.20. From the table, we see that if the true population proportion is equal to 0.50, we would be very unlikely to pick 0 or 1 red marble in our sample of 5 marbles. The probability of selecting 1 or 0 red marbles would be 0.1875. Therefore, if we let the significance level equal 0.1875, we can define the region of rejection as any sampled outcome that includes only 0 or 1 red marble (i.e., a sampled proportion equal to 0 or 0.20). We can define the region of acceptance as any sampled outcome that includes at least 2 red marbles. This is equivalent to a sampled proportion that is greater than or equal to 0.40.

• Test the null hypothesis . Since the sample proportion (0.40) is within the region of acceptance, we cannot reject the null hypothesis.

Example 2: Sampling Without Replacement

The Acme Advertising company has 25 clients. Account executives at Acme claim that 80 percent of these clients are very satisfied with the service they receive. To test that claim, Acme's CEO commissions a survey of 10 clients. Survey participants are randomly sampled, without replacement , from the client population. Six of the ten sampled customers (i.e., 60 percent) say that they are very satisfied. Based on the sample results, should the CEO accept or reject the hypothesis that 80 percent of Acme's clients are very satisfied. Use a significance level of 0.10.

Null hypothesis: P >= 0.80

Alternative hypothesis: P < 0.80

Given those inputs (a hypergeometric distribution where 20 of 25 clients are very satisfied), the sampling distribution of the proportion can be determined. It appears in the table below, which shows individual probabilities for single events and cumulative probabilities for multiple events. (Elsewhere on this website, we showed how to compute hypergeometric probabilities that form the body of the table.)

• Specify significance level . The significance level was set at 0.10. (This means that the probability of making a Type I error is 0.10, assuming that the null hypothesis is true.)

However, we can define a region of acceptance for which the significance level would be no more than 0.10. From the table, we see that if the true proportion of very satisfied clients is equal to 0.80, we would be very unlikely to have fewer than 7 very satisfied clients in our sample. The probability of having 6 or fewer very satisfied clients in the sample would be 0.064. Therefore, if we let the significance level equal 0.064, we can define the region of rejection as any sampled outcome that includes 6 or fewer very satisfied customers. We can define the region of acceptance as any sampled outcome that includes 7 or more very satisfied customers. This is equivalent to a sample proportion that is greater than or equal to 0.70.

• Test the null hypothesis . Since the sample proportion (0.60) is outside the region of acceptance, we cannot accept the null hypothesis at the 0.064 level of significance.

If you're seeing this message, it means we're having trouble loading external resources on our website.

If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.

To log in and use all the features of Khan Academy, please enable JavaScript in your browser.

AP®︎/College Statistics

Course: ap®︎/college statistics   >   unit 10, constructing hypotheses for a significance test about a proportion.

• Writing hypotheses for a test about a proportion
• Conditions for a z test about a proportion
• Reference: Conditions for inference on a proportion

Want to join the conversation?

• Upvote Button navigates to signup page
• Downvote Button navigates to signup page
• Flag Button navigates to signup page

Video transcript

Statistics Made Easy

How to Write a Null Hypothesis (5 Examples)

A hypothesis test uses sample data to determine whether or not some claim about a population parameter is true.

Whenever we perform a hypothesis test, we always write a null hypothesis and an alternative hypothesis, which take the following forms:

H 0 (Null Hypothesis): Population parameter =,  ≤, ≥ some value

H A  (Alternative Hypothesis): Population parameter <, >, ≠ some value

Note that the null hypothesis always contains the equal sign .

We interpret the hypotheses as follows:

Null hypothesis: The sample data provides no evidence to support some claim being made by an individual.

Alternative hypothesis: The sample data  does provide sufficient evidence to support the claim being made by an individual.

For example, suppose it’s assumed that the average height of a certain species of plant is 20 inches tall. However, one botanist claims the true average height is greater than 20 inches.

To test this claim, she may go out and collect a random sample of plants. She can then use this sample data to perform a hypothesis test using the following two hypotheses:

H 0 : μ ≤ 20 (the true mean height of plants is equal to or even less than 20 inches)

H A : μ > 20 (the true mean height of plants is greater than 20 inches)

If the sample data gathered by the botanist shows that the mean height of this species of plants is significantly greater than 20 inches, she can reject the null hypothesis and conclude that the mean height is greater than 20 inches.

Read through the following examples to gain a better understanding of how to write a null hypothesis in different situations.

Example 1: Weight of Turtles

A biologist wants to test whether or not the true mean weight of a certain species of turtles is 300 pounds. To test this, he goes out and measures the weight of a random sample of 40 turtles.

Here is how to write the null and alternative hypotheses for this scenario:

H 0 : μ = 300 (the true mean weight is equal to 300 pounds)

H A : μ ≠ 300 (the true mean weight is not equal to 300 pounds)

Example 2: Height of Males

It’s assumed that the mean height of males in a certain city is 68 inches. However, an independent researcher believes the true mean height is greater than 68 inches. To test this, he goes out and collects the height of 50 males in the city.

H 0 : μ ≤ 68 (the true mean height is equal to or even less than 68 inches)

H A : μ > 68 (the true mean height is greater than 68 inches)

Example 3: Graduation Rates

A university states that 80% of all students graduate on time. However, an independent researcher believes that less than 80% of all students graduate on time. To test this, she collects data on the proportion of students who graduated on time last year at the university.

H 0 : p ≥ 0.80 (the true proportion of students who graduate on time is 80% or higher)

H A : μ < 0.80 (the true proportion of students who graduate on time is less than 80%)

Example 4: Burger Weights

A food researcher wants to test whether or not the true mean weight of a burger at a certain restaurant is 7 ounces. To test this, he goes out and measures the weight of a random sample of 20 burgers from this restaurant.

H 0 : μ = 7 (the true mean weight is equal to 7 ounces)

H A : μ ≠ 7 (the true mean weight is not equal to 7 ounces)

Example 5: Citizen Support

A politician claims that less than 30% of citizens in a certain town support a certain law. To test this, he goes out and surveys 200 citizens on whether or not they support the law.

H 0 : p ≥ .30 (the true proportion of citizens who support the law is greater than or equal to 30%)

H A : μ < 0.30 (the true proportion of citizens who support the law is less than 30%)

Additional Resources

Introduction to Hypothesis Testing Introduction to Confidence Intervals An Explanation of P-Values and Statistical Significance

Published by Zach

Leave a reply cancel reply.

Your email address will not be published. Required fields are marked *

• Number Theory
• Data Structures
• Cornerstones

Hypothesis Tests for Proportions (Two Samples)

Suppose there was a particular characteristic of interest present in two separate populations, and you suspected that the proportions of members with this characteristic in these two populations were different. How could we test that claim?

To make our example concrete, let us suppose we want to know if the proportion of men that are taller than 5.5 ft is greater than the same for women. Taking a sample of 60 women and 45 men, we discover 27 men are taller than 5.5 ft, while only 18 women fall into this category.

Denoting the proportion of men in our sample that are taller than 5.5 ft by $\widehat{p}_m$ and the similar proportion for women in our sample by $\widehat{p}_f$, we have $$\widehat{p}_m = 0.60 \quad \textrm{ and } \quad \widehat{p}_f = 0.30$$ Clearly there is a difference in the sample proportions found -- but is this difference statistically significant?

Sounds like we need to perform a hypothesis test!

Formulating our null and alternative hypotheses, we have

Note, we could equivalently express these hypotheses as $$H_0 : p_m - p_f = 0 \quad \textrm{ and } \quad H_1 : p_m - p_f \neq 0$$ Writing the hypotheses in this way allows us to focus on a single distribution in our analysis -- the distribution of differences of sample proportions $\widehat{p}_m - \widehat{p}_f$.

To begin, we need some understanding of the nature of this distribution. Is it normally distributed? What is the mean? What is the standard deviation?

So both $\widehat{p}_m$ and $\widehat{p}_f$ are distributed normally.

Conveniently, if $X$ and $Y$ are normally distributed random variables, then $X-Y$ is also normally distributed, with mean and variance given by $\mu_{X-Y} = \mu_X - \mu_Y$ and $\sigma^2_{X-Y} = \sigma^2_X + \sigma^2_Y$.

Recalling that $\widehat{p}_m$ is normally distributed with mean $p_m$ and variance $\frac{p_m q_m}{n_m}$ and $\widehat{p}_f$ is normally distributed with mean $p_f$ and variance $\frac{p_f q_f}{n_f}$, we have the distribution of $\widehat{p}_m - \widehat{q}_f$ normal with mean and standard deviation given by $$\mu_{\widehat{p}_m - \widehat{q}_f} = p_m - p_f \quad \textrm{ and } \quad \sigma_{\widehat{p}_m - \widehat{q}_f} = \sqrt{\frac{p_m q_m}{n_m} + \frac{p_f q_f}{n_f}}$$

Given that the distribution of $\widehat{p}_m - \widehat{q}_f$ is normal, and knowledge of the mean and standard deviation, we could find $z$-scores for any observed differences to measure how unusual they are.

Unfortunately, the standard deviation is not known as it depends on $p_m$ and $p_f$, which are unknown. This is not a big hurdle, however, as we can play the same game as we did with hypothesis tests for a proportion involving a single sample. We can approximate the standard deviation with the standard error: $$SE(\widehat{p}_m - \widehat{p}_f) = \sqrt{\frac{\widehat{p}_m \widehat{q}_m}{n_m} + \frac{\widehat{p}_f \widehat{q}_f}{n_f}}$$

However, we can do even better than that in this situation. There are two proportions in the standard error formula above -- but look at our null hypothesis. It says that the proportions they approximate should be equal. Under the assumption of the null hypothesis then, both $\widehat{p}_m$ and $\widehat{p}_f$ are approximations of the same proportion. Consequently, we can combine them (or "pool" them) into a single best approximation of this common proportion, called the pooled proportion .

In general, whenever we combine data from different sources or different groups because we believe they really came from the same underlying population, it is called pooling .

Denoting the pooled proportion by $\overline{p}$, we have $$\begin{array}{rcl} \overline{p} &=& \displaystyle{\frac{n_m \widehat{p}_m + n_f \widehat{p}_f}{n_m + n_f}}\\\\ &=& \displaystyle{\frac{27 + 18}{60 + 45}}\\\\ &\doteq& 0.4286 \end{array}$$

Replacing the approximations $\widehat{p}_m$ and $\widehat{p}_f$ of $p_m = p_f$ with the better, pooled approximation of $\overline{p}$ and defining $\overline{q} = 1 - \overline{p}$, our standard error becomes $$\begin{array}{rcl} SE(\widehat{p}_m - \widehat{p}_f) &=& \displaystyle{\sqrt{\frac{\overline{p}\overline{q}}{n_m} + \frac{\overline{p}\overline{q}}{n_f}}}\\ &=& \displaystyle{\sqrt{\overline{p}\overline{q} \left(\frac{1}{n_m} + \frac{1}{n_f} \right)}} \end{array}$$

Finally, using this standard error as an approximation to the standard deviation for the normal distribution of $\widehat{p}_m - \widehat{p}_f$ centered at $p_m - p_f$ (hypothesized to be zero), we can find a test statistic ($z$-score) for the difference of proportions seen in our two samples: $$z = \frac{(\widehat{p}_m - \widehat{p}_f) - 0}{\displaystyle{\sqrt{\overline{p}\overline{q} \left(\frac{1}{n_m} + \frac{1}{n_f} \right)}}}$$

Calculating the actual value of this test statistic in this example, the rest of the hypothesis test proceeds in the normal way. $$z \doteq \frac{(0.60 - 0.30) - 0}{0.09759} \doteq 3.07$$ At the $\alpha = 0.05$ significance level, the critical values are $\pm1.96$, so this test statistic clearly falls in the rejection region. Consequently, we reject the null hypothesis that the proportions are the same, making the inference that the proportions of men and women that are taller than 5.5 ft are significantly different.

Confidence Intervals for Differences in Proportions (Two Sample)

Continuing with the example discussed above -- one can build a confidence interval for the true difference $p_m - p_f$ in a similar way.

The best point estimate (and thus, the center of the confidence interval) is not surprisingly $\widehat{p}_m - \widehat{p}_f$.

As for the margin of error, $\displaystyle{E = z_{\alpha/2} \sigma}$, we approximate $\sigma$ with the standard error: $$SE(\widehat{p}_m - \widehat{p}_f) = \sqrt{\frac{\widehat{p}_m \widehat{q}_m}{n_m} + \frac{\widehat{p}_f \widehat{q}_f}{n_f}}$$ Notice that we can't pool the sample proportions in this case, as there is no null hypothesis allowing us to assume $p_m$ and $p_f$ are equal.

• Math Article

Null Hypothesis

In mathematics, Statistics deals with the study of research and surveys on the numerical data. For taking surveys, we have to define the hypothesis. Generally, there are two types of hypothesis. One is a null hypothesis, and another is an alternative hypothesis .

In probability and statistics, the null hypothesis is a comprehensive statement or default status that there is zero happening or nothing happening. For example, there is no connection among groups or no association between two measured events. It is generally assumed here that the hypothesis is true until any other proof has been brought into the light to deny the hypothesis. Let us learn more here with definition, symbol, principle, types and example, in this article.

Table of contents:

• Comparison with Alternative Hypothesis

Null Hypothesis Definition

The null hypothesis is a kind of hypothesis which explains the population parameter whose purpose is to test the validity of the given experimental data. This hypothesis is either rejected or not rejected based on the viability of the given population or sample . In other words, the null hypothesis is a hypothesis in which the sample observations results from the chance. It is said to be a statement in which the surveyors wants to examine the data. It is denoted by H 0 .

Null Hypothesis Symbol

In statistics, the null hypothesis is usually denoted by letter H with subscript ‘0’ (zero), such that H 0 . It is pronounced as H-null or H-zero or H-nought. At the same time, the alternative hypothesis expresses the observations determined by the non-random cause. It is represented by H 1 or H a .

Null Hypothesis Principle

The principle followed for null hypothesis testing is, collecting the data and determining the chances of a given set of data during the study on some random sample, assuming that the null hypothesis is true. In case if the given data does not face the expected null hypothesis, then the outcome will be quite weaker, and they conclude by saying that the given set of data does not provide strong evidence against the null hypothesis because of insufficient evidence. Finally, the researchers tend to reject that.

Null Hypothesis Formula

Here, the hypothesis test formulas are given below for reference.

The formula for the null hypothesis is:

H 0 :  p = p 0

The formula for the alternative hypothesis is:

H a = p >p 0 , < p 0 ≠ p 0

The formula for the test static is:

Remember that,  p 0  is the null hypothesis and p – hat is the sample proportion.

Also, read:

Types of Null Hypothesis

There are different types of hypothesis. They are:

Simple Hypothesis

It completely specifies the population distribution. In this method, the sampling distribution is the function of the sample size.

Composite Hypothesis

The composite hypothesis is one that does not completely specify the population distribution.

Exact Hypothesis

Exact hypothesis defines the exact value of the parameter. For example μ= 50

Inexact Hypothesis

This type of hypothesis does not define the exact value of the parameter. But it denotes a specific range or interval. For example 45< μ <60

Null Hypothesis Rejection

Sometimes the null hypothesis is rejected too. If this hypothesis is rejected means, that research could be invalid. Many researchers will neglect this hypothesis as it is merely opposite to the alternate hypothesis. It is a better practice to create a hypothesis and test it. The goal of researchers is not to reject the hypothesis. But it is evident that a perfect statistical model is always associated with the failure to reject the null hypothesis.

How do you Find the Null Hypothesis?

The null hypothesis says there is no correlation between the measured event (the dependent variable) and the independent variable. We don’t have to believe that the null hypothesis is true to test it. On the contrast, you will possibly assume that there is a connection between a set of variables ( dependent and independent).

When is Null Hypothesis Rejected?

The null hypothesis is rejected using the P-value approach. If the P-value is less than or equal to the α, there should be a rejection of the null hypothesis in favour of the alternate hypothesis. In case, if P-value is greater than α, the null hypothesis is not rejected.

Null Hypothesis and Alternative Hypothesis

Now, let us discuss the difference between the null hypothesis and the alternative hypothesis.

Null Hypothesis Examples

Here, some of the examples of the null hypothesis are given below. Go through the below ones to understand the concept of the null hypothesis in a better way.

If a medicine reduces the risk of cardiac stroke, then the null hypothesis should be “the medicine does not reduce the chance of cardiac stroke”. This testing can be performed by the administration of a drug to a certain group of people in a controlled way. If the survey shows that there is a significant change in the people, then the hypothesis is rejected.

Few more examples are:

1). Are there is 100% chance of getting affected by dengue?

Ans: There could be chances of getting affected by dengue but not 100%.

2). Do teenagers are using mobile phones more than grown-ups to access the internet?

Ans: Age has no limit on using mobile phones to access the internet.

3). Does having apple daily will not cause fever?

Ans: Having apple daily does not assure of not having fever, but increases the immunity to fight against such diseases.

4). Do the children more good in doing mathematical calculations than grown-ups?

Ans: Age has no effect on Mathematical skills.

In many common applications, the choice of the null hypothesis is not automated, but the testing and calculations may be automated. Also, the choice of the null hypothesis is completely based on previous experiences and inconsistent advice. The choice can be more complicated and based on the variety of applications and the diversity of the objectives. 

The main limitation for the choice of the null hypothesis is that the hypothesis suggested by the data is based on the reasoning which proves nothing. It means that if some hypothesis provides a summary of the data set, then there would be no value in the testing of the hypothesis on the particular set of data. 

Frequently Asked Questions on Null Hypothesis

What is meant by the null hypothesis.

In Statistics, a null hypothesis is a type of hypothesis which explains the population parameter whose purpose is to test the validity of the given experimental data.

What are the benefits of hypothesis testing?

Hypothesis testing is defined as a form of inferential statistics, which allows making conclusions from the entire population based on the sample representative.

When a null hypothesis is accepted and rejected?

The null hypothesis is either accepted or rejected in terms of the given data. If P-value is less than α, then the null hypothesis is rejected in favor of the alternative hypothesis, and if the P-value is greater than α, then the null hypothesis is accepted in favor of the alternative hypothesis.

Why is the null hypothesis important?

The importance of the null hypothesis is that it provides an approximate description of the phenomena of the given data. It allows the investigators to directly test the relational statement in a research study.

How to accept or reject the null hypothesis in the chi-square test?

If the result of the chi-square test is bigger than the critical value in the table, then the data does not fit the model, which represents the rejection of the null hypothesis.

Put your understanding of this concept to test by answering a few MCQs. Click ‘Start Quiz’ to begin!

Select the correct answer and click on the “Finish” button Check your score and answers at the end of the quiz

Visit BYJU’S for all Maths related queries and study materials

Your result is as below

Request OTP on Voice Call

• Share Share

Register with BYJU'S & Download Free PDFs

Register with byju's & watch live videos.

• Study Guides
• Homework Questions

Section 9 Lab Part 1 Intro and Proportions

User Preferences

Content preview.

Arcu felis bibendum ut tristique et egestas quis:

• Ut enim ad minim veniam, quis nostrud exercitation ullamco laboris
• Duis aute irure dolor in reprehenderit in voluptate
• Excepteur sint occaecat cupidatat non proident

Keyboard Shortcuts

5.5 - hypothesis testing for two-sample proportions.

We are now going to develop the hypothesis test for the difference of two proportions for independent samples. The hypothesis test follows the same steps as one group.

These notes are going to go into a little bit of math and formulas to help demonstrate the logic behind hypothesis testing for two groups. If this starts to get a little confusion, just skim over it for a general understanding! Remember we can rely on the software to do the calculations for us, but it is good to have a basic understanding of the logic!

We will use the sampling distribution of \(\hat{p}_1-\hat{p}_2\) as we did for the confidence interval.

For a test for two proportions, we are interested in the difference between two groups. If the difference is zero, then they are not different (i.e., they are equal). Therefore, the null hypothesis will always be:

\(H_0\colon p_1-p_2=0\)

Another way to look at it is \(H_0\colon p_1=p_2\). This is worth stopping to think about. Remember, in hypothesis testing, we assume the null hypothesis is true. In this case, it means that \(p_1\) and \(p_2\) are equal. Under this assumption, then \(\hat{p}_1\) and \(\hat{p}_2\) are both estimating the same proportion. Think of this proportion as \(p^*\).

Therefore, the sampling distribution of both proportions, \(\hat{p}_1\) and \(\hat{p}_2\), will, under certain conditions, be approximately normal centered around \(p^*\), with standard error \(\sqrt{\dfrac{p^*(1-p^*)}{n_i}}\), for \(i=1, 2\).

We take this into account by finding an estimate for this \(p^*\) using the two-sample proportions. We can calculate an estimate of \(p^*\) using the following formula:

\(\hat{p}^*=\dfrac{x_1+x_2}{n_1+n_2}\)

This value is the total number in the desired categories \((x_1+x_2)\) from both samples over the total number of sampling units in the combined sample \((n_1+n_2)\).

Putting everything together, if we assume \(p_1=p_2\), then the sampling distribution of \(\hat{p}_1-\hat{p}_2\) will be approximately normal with mean 0 and standard error of \(\sqrt{p^*(1-p^*)\left(\frac{1}{n_1}+\frac{1}{n_2}\right)}\), under certain conditions.

\(z^*=\dfrac{(\hat{p}_1-\hat{p}_2)-0}{\sqrt{\hat{p}^*(1-\hat{p}^*)\left(\dfrac{1}{n_1}+\dfrac{1}{n_2}\right)}}\)

...will follow a standard normal distribution.

Finally, we can develop our hypothesis test for \(p_1-p_2\).

Hypothesis Testing for Two-Sample Proportions

Conditions :

\(n_1\hat{p}_1\), \(n_1(1-\hat{p}_1)\), \(n_2\hat{p}_2\), and \(n_2(1-\hat{p}_2)\) are all greater than five

Test Statistic:

\(z^*=\dfrac{\hat{p}_1-\hat{p}_2-0}{\sqrt{\hat{p}^*(1-\hat{p}^*)\left(\dfrac{1}{n_1}+\dfrac{1}{n_2}\right)}}\)

...where \(\hat{p}^*=\dfrac{x_1+x_2}{n_1+n_2}\).

The critical values, p-values, and decisions will all follow the same steps as those from a hypothesis test for a one-sample proportion.