hypothesis testing of means and proportions

Hypothesis Testing for Means & Proportions

Lisa Sullivan, PhD

Professor of Biostatistics

Boston University School of Public Health

Introduction

This is the first of three modules that will addresses the second area of statistical inference, which is hypothesis testing, in which a specific statement or hypothesis is generated about a population parameter, and sample statistics are used to assess the likelihood that the hypothesis is true. The hypothesis is based on available information and the investigator's belief about the population parameters. The process of hypothesis testing involves setting up two competing hypotheses, the null hypothesis and the alternate hypothesis. One selects a random sample (or multiple samples when there are more comparison groups), computes summary statistics and then assesses the likelihood that the sample data support the research or alternative hypothesis. Similar to estimation, the process of hypothesis testing is based on probability theory and the Central Limit Theorem.  

This module will focus on hypothesis testing for means and proportions. The next two modules in this series will address analysis of variance and chi-squared tests. 

Learning Objectives

After completing this module, the student will be able to:

• Define null and research hypothesis, test statistic, level of significance and decision rule
• Distinguish between Type I and Type II errors and discuss the implications of each
• Explain the difference between one and two sided tests of hypothesis
• Estimate and interpret p-values
• Explain the relationship between confidence interval estimates and p-values in drawing inferences
• Differentiate hypothesis testing procedures based on type of outcome variable and number of sample

Introduction to Hypothesis Testing

Techniques for hypothesis testing  .

The techniques for hypothesis testing depend on

• the type of outcome variable being analyzed (continuous, dichotomous, discrete)
• the number of comparison groups in the investigation
• whether the comparison groups are independent (i.e., physically separate such as men versus women) or dependent (i.e., matched or paired such as pre- and post-assessments on the same participants).

In estimation we focused explicitly on techniques for one and two samples and discussed estimation for a specific parameter (e.g., the mean or proportion of a population), for differences (e.g., difference in means, the risk difference) and ratios (e.g., the relative risk and odds ratio). Here we will focus on procedures for one and two samples when the outcome is either continuous (and we focus on means) or dichotomous (and we focus on proportions).

General Approach: A Simple Example

The Centers for Disease Control (CDC) reported on trends in weight, height and body mass index from the 1960's through 2002. 1 The general trend was that Americans were much heavier and slightly taller in 2002 as compared to 1960; both men and women gained approximately 24 pounds, on average, between 1960 and 2002.   In 2002, the mean weight for men was reported at 191 pounds. Suppose that an investigator hypothesizes that weights are even higher in 2006 (i.e., that the trend continued over the subsequent 4 years). The research hypothesis is that the mean weight in men in 2006 is more than 191 pounds. The null hypothesis is that there is no change in weight, and therefore the mean weight is still 191 pounds in 2006.  

In order to test the hypotheses, we select a random sample of American males in 2006 and measure their weights. Suppose we have resources available to recruit n=100 men into our sample. We weigh each participant and compute summary statistics on the sample data. Suppose in the sample we determine the following:

Do the sample data support the null or research hypothesis? The sample mean of 197.1 is numerically higher than 191. However, is this difference more than would be expected by chance? In hypothesis testing, we assume that the null hypothesis holds until proven otherwise. We therefore need to determine the likelihood of observing a sample mean of 197.1 or higher when the true population mean is 191 (i.e., if the null hypothesis is true or under the null hypothesis). We can compute this probability using the Central Limit Theorem. Specifically,

(Notice that we use the sample standard deviation in computing the Z score. This is generally an appropriate substitution as long as the sample size is large, n > 30. Thus, there is less than a 1% probability of observing a sample mean as large as 197.1 when the true population mean is 191. Do you think that the null hypothesis is likely true? Based on how unlikely it is to observe a sample mean of 197.1 under the null hypothesis (i.e., <1% probability), we might infer, from our data, that the null hypothesis is probably not true.

Suppose that the sample data had turned out differently. Suppose that we instead observed the following in 2006:

How likely it is to observe a sample mean of 192.1 or higher when the true population mean is 191 (i.e., if the null hypothesis is true)? We can again compute this probability using the Central Limit Theorem. Specifically,

There is a 33.4% probability of observing a sample mean as large as 192.1 when the true population mean is 191. Do you think that the null hypothesis is likely true?  

Neither of the sample means that we obtained allows us to know with certainty whether the null hypothesis is true or not. However, our computations suggest that, if the null hypothesis were true, the probability of observing a sample mean >197.1 is less than 1%. In contrast, if the null hypothesis were true, the probability of observing a sample mean >192.1 is about 33%. We can't know whether the null hypothesis is true, but the sample that provided a mean value of 197.1 provides much stronger evidence in favor of rejecting the null hypothesis, than the sample that provided a mean value of 192.1. Note that this does not mean that a sample mean of 192.1 indicates that the null hypothesis is true; it just doesn't provide compelling evidence to reject it.

In essence, hypothesis testing is a procedure to compute a probability that reflects the strength of the evidence (based on a given sample) for rejecting the null hypothesis. In hypothesis testing, we determine a threshold or cut-off point (called the critical value) to decide when to believe the null hypothesis and when to believe the research hypothesis. It is important to note that it is possible to observe any sample mean when the true population mean is true (in this example equal to 191), but some sample means are very unlikely. Based on the two samples above it would seem reasonable to believe the research hypothesis when x̄ = 197.1, but to believe the null hypothesis when x̄ =192.1. What we need is a threshold value such that if x̄ is above that threshold then we believe that H 1 is true and if x̄ is below that threshold then we believe that H 0 is true. The difficulty in determining a threshold for x̄ is that it depends on the scale of measurement. In this example, the threshold, sometimes called the critical value, might be 195 (i.e., if the sample mean is 195 or more then we believe that H 1 is true and if the sample mean is less than 195 then we believe that H 0 is true). Suppose we are interested in assessing an increase in blood pressure over time, the critical value will be different because blood pressures are measured in millimeters of mercury (mmHg) as opposed to in pounds. In the following we will explain how the critical value is determined and how we handle the issue of scale.

First, to address the issue of scale in determining the critical value, we convert our sample data (in particular the sample mean) into a Z score. We know from the module on probability that the center of the Z distribution is zero and extreme values are those that exceed 2 or fall below -2. Z scores above 2 and below -2 represent approximately 5% of all Z values. If the observed sample mean is close to the mean specified in H 0 (here m =191), then Z will be close to zero. If the observed sample mean is much larger than the mean specified in H 0 , then Z will be large.  

In hypothesis testing, we select a critical value from the Z distribution. This is done by first determining what is called the level of significance, denoted α ("alpha"). What we are doing here is drawing a line at extreme values. The level of significance is the probability that we reject the null hypothesis (in favor of the alternative) when it is actually true and is also called the Type I error rate.

α = Level of significance = P(Type I error) = P(Reject H 0 | H 0 is true).

Because α is a probability, it ranges between 0 and 1. The most commonly used value in the medical literature for α is 0.05, or 5%. Thus, if an investigator selects α=0.05, then they are allowing a 5% probability of incorrectly rejecting the null hypothesis in favor of the alternative when the null is in fact true. Depending on the circumstances, one might choose to use a level of significance of 1% or 10%. For example, if an investigator wanted to reject the null only if there were even stronger evidence than that ensured with α=0.05, they could choose a =0.01as their level of significance. The typical values for α are 0.01, 0.05 and 0.10, with α=0.05 the most commonly used value.  

Suppose in our weight study we select α=0.05. We need to determine the value of Z that holds 5% of the values above it (see below).

The critical value of Z for α =0.05 is Z = 1.645 (i.e., 5% of the distribution is above Z=1.645). With this value we can set up what is called our decision rule for the test. The rule is to reject H 0 if the Z score is 1.645 or more.  

With the first sample we have

Because 2.38 > 1.645, we reject the null hypothesis. (The same conclusion can be drawn by comparing the 0.0087 probability of observing a sample mean as extreme as 197.1 to the level of significance of 0.05. If the observed probability is smaller than the level of significance we reject H 0 ). Because the Z score exceeds the critical value, we conclude that the mean weight for men in 2006 is more than 191 pounds, the value reported in 2002. If we observed the second sample (i.e., sample mean =192.1), we would not be able to reject the null hypothesis because the Z score is 0.43 which is not in the rejection region (i.e., the region in the tail end of the curve above 1.645). With the second sample we do not have sufficient evidence (because we set our level of significance at 5%) to conclude that weights have increased. Again, the same conclusion can be reached by comparing probabilities. The probability of observing a sample mean as extreme as 192.1 is 33.4% which is not below our 5% level of significance.

Hypothesis Testing: Upper-, Lower, and Two Tailed Tests

The procedure for hypothesis testing is based on the ideas described above. Specifically, we set up competing hypotheses, select a random sample from the population of interest and compute summary statistics. We then determine whether the sample data supports the null or alternative hypotheses. The procedure can be broken down into the following five steps.  

• Step 1. Set up hypotheses and select the level of significance α.

H 0 : Null hypothesis (no change, no difference);  

H 1 : Research hypothesis (investigator's belief); α =0.05

• Step 2. Select the appropriate test statistic.  

The test statistic is a single number that summarizes the sample information.   An example of a test statistic is the Z statistic computed as follows:

When the sample size is small, we will use t statistics (just as we did when constructing confidence intervals for small samples). As we present each scenario, alternative test statistics are provided along with conditions for their appropriate use.

• Step 3.  Set up decision rule.  

The decision rule is a statement that tells under what circumstances to reject the null hypothesis. The decision rule is based on specific values of the test statistic (e.g., reject H 0 if Z > 1.645). The decision rule for a specific test depends on 3 factors: the research or alternative hypothesis, the test statistic and the level of significance. Each is discussed below.

• The decision rule depends on whether an upper-tailed, lower-tailed, or two-tailed test is proposed. In an upper-tailed test the decision rule has investigators reject H 0 if the test statistic is larger than the critical value. In a lower-tailed test the decision rule has investigators reject H 0 if the test statistic is smaller than the critical value.  In a two-tailed test the decision rule has investigators reject H 0 if the test statistic is extreme, either larger than an upper critical value or smaller than a lower critical value.
• The exact form of the test statistic is also important in determining the decision rule. If the test statistic follows the standard normal distribution (Z), then the decision rule will be based on the standard normal distribution. If the test statistic follows the t distribution, then the decision rule will be based on the t distribution. The appropriate critical value will be selected from the t distribution again depending on the specific alternative hypothesis and the level of significance.  
• The third factor is the level of significance. The level of significance which is selected in Step 1 (e.g., α =0.05) dictates the critical value.   For example, in an upper tailed Z test, if α =0.05 then the critical value is Z=1.645.  

The following figures illustrate the rejection regions defined by the decision rule for upper-, lower- and two-tailed Z tests with α=0.05. Notice that the rejection regions are in the upper, lower and both tails of the curves, respectively. The decision rules are written below each figure.

Rejection Region for Lower-Tailed Z Test (H 1 : μ < μ 0 ) with α =0.05

The decision rule is: Reject H 0 if Z < 1.645.

Rejection Region for Two-Tailed Z Test (H 1 : μ ≠ μ 0 ) with α =0.05

The decision rule is: Reject H 0 if Z < -1.960 or if Z > 1.960.

The complete table of critical values of Z for upper, lower and two-tailed tests can be found in the table of Z values to the right in "Other Resources."

Critical values of t for upper, lower and two-tailed tests can be found in the table of t values in "Other Resources."

• Step 4. Compute the test statistic.  

Here we compute the test statistic by substituting the observed sample data into the test statistic identified in Step 2.

• Step 5. Conclusion.  

The final conclusion is made by comparing the test statistic (which is a summary of the information observed in the sample) to the decision rule. The final conclusion will be either to reject the null hypothesis (because the sample data are very unlikely if the null hypothesis is true) or not to reject the null hypothesis (because the sample data are not very unlikely).  

If the null hypothesis is rejected, then an exact significance level is computed to describe the likelihood of observing the sample data assuming that the null hypothesis is true. The exact level of significance is called the p-value and it will be less than the chosen level of significance if we reject H 0 .

Statistical computing packages provide exact p-values as part of their standard output for hypothesis tests. In fact, when using a statistical computing package, the steps outlined about can be abbreviated. The hypotheses (step 1) should always be set up in advance of any analysis and the significance criterion should also be determined (e.g., α =0.05). Statistical computing packages will produce the test statistic (usually reporting the test statistic as t) and a p-value. The investigator can then determine statistical significance using the following: If p < α then reject H 0 .  

• Step 1. Set up hypotheses and determine level of significance

H 0 : μ = 191 H 1 : μ > 191                 α =0.05

The research hypothesis is that weights have increased, and therefore an upper tailed test is used.

• Step 2. Select the appropriate test statistic.

Because the sample size is large (n > 30) the appropriate test statistic is

• Step 3. Set up decision rule.  

In this example, we are performing an upper tailed test (H 1 : μ> 191), with a Z test statistic and selected α =0.05.   Reject H 0 if Z > 1.645.

We now substitute the sample data into the formula for the test statistic identified in Step 2.  

We reject H 0 because 2.38 > 1.645. We have statistically significant evidence at a =0.05, to show that the mean weight in men in 2006 is more than 191 pounds. Because we rejected the null hypothesis, we now approximate the p-value which is the likelihood of observing the sample data if the null hypothesis is true. An alternative definition of the p-value is the smallest level of significance where we can still reject H 0 . In this example, we observed Z=2.38 and for α=0.05, the critical value was 1.645. Because 2.38 exceeded 1.645 we rejected H 0 . In our conclusion we reported a statistically significant increase in mean weight at a 5% level of significance. Using the table of critical values for upper tailed tests, we can approximate the p-value. If we select α=0.025, the critical value is 1.96, and we still reject H 0 because 2.38 > 1.960. If we select α=0.010 the critical value is 2.326, and we still reject H 0 because 2.38 > 2.326. However, if we select α=0.005, the critical value is 2.576, and we cannot reject H 0 because 2.38 < 2.576. Therefore, the smallest α where we still reject H 0 is 0.010. This is the p-value. A statistical computing package would produce a more precise p-value which would be in between 0.005 and 0.010. Here we are approximating the p-value and would report p < 0.010.                  

Type I and Type II Errors

In all tests of hypothesis, there are two types of errors that can be committed. The first is called a Type I error and refers to the situation where we incorrectly reject H 0 when in fact it is true. This is also called a false positive result (as we incorrectly conclude that the research hypothesis is true when in fact it is not). When we run a test of hypothesis and decide to reject H 0 (e.g., because the test statistic exceeds the critical value in an upper tailed test) then either we make a correct decision because the research hypothesis is true or we commit a Type I error. The different conclusions are summarized in the table below. Note that we will never know whether the null hypothesis is really true or false (i.e., we will never know which row of the following table reflects reality).

Table - Conclusions in Test of Hypothesis

In the first step of the hypothesis test, we select a level of significance, α, and α= P(Type I error). Because we purposely select a small value for α, we control the probability of committing a Type I error. For example, if we select α=0.05, and our test tells us to reject H 0 , then there is a 5% probability that we commit a Type I error. Most investigators are very comfortable with this and are confident when rejecting H 0 that the research hypothesis is true (as it is the more likely scenario when we reject H 0 ).

When we run a test of hypothesis and decide not to reject H 0 (e.g., because the test statistic is below the critical value in an upper tailed test) then either we make a correct decision because the null hypothesis is true or we commit a Type II error. Beta (β) represents the probability of a Type II error and is defined as follows: β=P(Type II error) = P(Do not Reject H 0 | H 0 is false). Unfortunately, we cannot choose β to be small (e.g., 0.05) to control the probability of committing a Type II error because β depends on several factors including the sample size, α, and the research hypothesis. When we do not reject H 0 , it may be very likely that we are committing a Type II error (i.e., failing to reject H 0 when in fact it is false). Therefore, when tests are run and the null hypothesis is not rejected we often make a weak concluding statement allowing for the possibility that we might be committing a Type II error. If we do not reject H 0 , we conclude that we do not have significant evidence to show that H 1 is true. We do not conclude that H 0 is true.

 The most common reason for a Type II error is a small sample size.

Tests with One Sample, Continuous Outcome

Hypothesis testing applications with a continuous outcome variable in a single population are performed according to the five-step procedure outlined above. A key component is setting up the null and research hypotheses. The objective is to compare the mean in a single population to known mean (μ 0 ). The known value is generally derived from another study or report, for example a study in a similar, but not identical, population or a study performed some years ago. The latter is called a historical control. It is important in setting up the hypotheses in a one sample test that the mean specified in the null hypothesis is a fair and reasonable comparator. This will be discussed in the examples that follow.

Test Statistics for Testing H 0 : μ= μ 0

• if n > 30
• if n < 30

Note that statistical computing packages will use the t statistic exclusively and make the necessary adjustments for comparing the test statistic to appropriate values from probability tables to produce a p-value. 

The National Center for Health Statistics (NCHS) published a report in 2005 entitled Health, United States, containing extensive information on major trends in the health of Americans. Data are provided for the US population as a whole and for specific ages, sexes and races.  The NCHS report indicated that in 2002 Americans paid an average of $3,302 per year on health care and prescription drugs. An investigator hypothesizes that in 2005 expenditures have decreased primarily due to the availability of generic drugs. To test the hypothesis, a sample of 100 Americans are selected and their expenditures on health care and prescription drugs in 2005 are measured.   The sample data are summarized as follows: n=100, x̄

=$3,190 and s=$890. Is there statistical evidence of a reduction in expenditures on health care and prescription drugs in 2005? Is the sample mean of $3,190 evidence of a true reduction in the mean or is it within chance fluctuation? We will run the test using the five-step approach. 

• Step 1.  Set up hypotheses and determine level of significance

H 0 : μ = 3,302 H 1 : μ < 3,302           α =0.05

The research hypothesis is that expenditures have decreased, and therefore a lower-tailed test is used.

This is a lower tailed test, using a Z statistic and a 5% level of significance.   Reject H 0 if Z < -1.645.

•   Step 4. Compute the test statistic.  

We do not reject H 0 because -1.26 > -1.645. We do not have statistically significant evidence at α=0.05 to show that the mean expenditures on health care and prescription drugs are lower in 2005 than the mean of $3,302 reported in 2002.  

Recall that when we fail to reject H 0 in a test of hypothesis that either the null hypothesis is true (here the mean expenditures in 2005 are the same as those in 2002 and equal to $3,302) or we committed a Type II error (i.e., we failed to reject H 0 when in fact it is false). In summarizing this test, we conclude that we do not have sufficient evidence to reject H 0 . We do not conclude that H 0 is true, because there may be a moderate to high probability that we committed a Type II error. It is possible that the sample size is not large enough to detect a difference in mean expenditures.      

The NCHS reported that the mean total cholesterol level in 2002 for all adults was 203. Total cholesterol levels in participants who attended the seventh examination of the Offspring in the Framingham Heart Study are summarized as follows: n=3,310, x̄ =200.3, and s=36.8. Is there statistical evidence of a difference in mean cholesterol levels in the Framingham Offspring?

Here we want to assess whether the sample mean of 200.3 in the Framingham sample is statistically significantly different from 203 (i.e., beyond what we would expect by chance). We will run the test using the five-step approach.

H 0 : μ= 203 H 1 : μ≠ 203                       α=0.05

The research hypothesis is that cholesterol levels are different in the Framingham Offspring, and therefore a two-tailed test is used.

•   Step 3. Set up decision rule.  

This is a two-tailed test, using a Z statistic and a 5% level of significance. Reject H 0 if Z < -1.960 or is Z > 1.960.

We reject H 0 because -4.22 ≤ -1. .960. We have statistically significant evidence at α=0.05 to show that the mean total cholesterol level in the Framingham Offspring is different from the national average of 203 reported in 2002.   Because we reject H 0 , we also approximate a p-value. Using the two-sided significance levels, p < 0.0001.  

Statistical Significance versus Clinical (Practical) Significance

This example raises an important concept of statistical versus clinical or practical significance. From a statistical standpoint, the total cholesterol levels in the Framingham sample are highly statistically significantly different from the national average with p < 0.0001 (i.e., there is less than a 0.01% chance that we are incorrectly rejecting the null hypothesis). However, the sample mean in the Framingham Offspring study is 200.3, less than 3 units different from the national mean of 203. The reason that the data are so highly statistically significant is due to the very large sample size. It is always important to assess both statistical and clinical significance of data. This is particularly relevant when the sample size is large. Is a 3 unit difference in total cholesterol a meaningful difference?  

Consider again the NCHS-reported mean total cholesterol level in 2002 for all adults of 203. Suppose a new drug is proposed to lower total cholesterol. A study is designed to evaluate the efficacy of the drug in lowering cholesterol.   Fifteen patients are enrolled in the study and asked to take the new drug for 6 weeks. At the end of 6 weeks, each patient's total cholesterol level is measured and the sample statistics are as follows:   n=15, x̄ =195.9 and s=28.7. Is there statistical evidence of a reduction in mean total cholesterol in patients after using the new drug for 6 weeks? We will run the test using the five-step approach. 

H 0 : μ= 203 H 1 : μ< 203                   α=0.05

•  Step 2. Select the appropriate test statistic.  

Because the sample size is small (n<30) the appropriate test statistic is

This is a lower tailed test, using a t statistic and a 5% level of significance. In order to determine the critical value of t, we need degrees of freedom, df, defined as df=n-1. In this example df=15-1=14. The critical value for a lower tailed test with df=14 and a =0.05 is -2.145 and the decision rule is as follows:   Reject H 0 if t < -2.145.

We do not reject H 0 because -0.96 > -2.145. We do not have statistically significant evidence at α=0.05 to show that the mean total cholesterol level is lower than the national mean in patients taking the new drug for 6 weeks. Again, because we failed to reject the null hypothesis we make a weaker concluding statement allowing for the possibility that we may have committed a Type II error (i.e., failed to reject H 0 when in fact the drug is efficacious).

This example raises an important issue in terms of study design. In this example we assume in the null hypothesis that the mean cholesterol level is 203. This is taken to be the mean cholesterol level in patients without treatment. Is this an appropriate comparator? Alternative and potentially more efficient study designs to evaluate the effect of the new drug could involve two treatment groups, where one group receives the new drug and the other does not, or we could measure each patient's baseline or pre-treatment cholesterol level and then assess changes from baseline to 6 weeks post-treatment. These designs are also discussed here.

Video - Comparing a Sample Mean to Known Population Mean (8:20)

Link to transcript of the video

Tests with One Sample, Dichotomous Outcome

Hypothesis testing applications with a dichotomous outcome variable in a single population are also performed according to the five-step procedure. Similar to tests for means, a key component is setting up the null and research hypotheses. The objective is to compare the proportion of successes in a single population to a known proportion (p 0 ). That known proportion is generally derived from another study or report and is sometimes called a historical control. It is important in setting up the hypotheses in a one sample test that the proportion specified in the null hypothesis is a fair and reasonable comparator.    

In one sample tests for a dichotomous outcome, we set up our hypotheses against an appropriate comparator. We select a sample and compute descriptive statistics on the sample data. Specifically, we compute the sample size (n) and the sample proportion which is computed by taking the ratio of the number of successes to the sample size,

We then determine the appropriate test statistic (Step 2) for the hypothesis test. The formula for the test statistic is given below.

Test Statistic for Testing H 0 : p = p 0

if min(np 0 , n(1-p 0 )) > 5

The formula above is appropriate for large samples, defined when the smaller of np 0 and n(1-p 0 ) is at least 5. This is similar, but not identical, to the condition required for appropriate use of the confidence interval formula for a population proportion, i.e.,

Here we use the proportion specified in the null hypothesis as the true proportion of successes rather than the sample proportion. If we fail to satisfy the condition, then alternative procedures, called exact methods must be used to test the hypothesis about the population proportion.

Example:  

The NCHS report indicated that in 2002 the prevalence of cigarette smoking among American adults was 21.1%.  Data on prevalent smoking in n=3,536 participants who attended the seventh examination of the Offspring in the Framingham Heart Study indicated that 482/3,536 = 13.6% of the respondents were currently smoking at the time of the exam. Suppose we want to assess whether the prevalence of smoking is lower in the Framingham Offspring sample given the focus on cardiovascular health in that community. Is there evidence of a statistically lower prevalence of smoking in the Framingham Offspring study as compared to the prevalence among all Americans?

H 0 : p = 0.211 H 1 : p < 0.211                     α=0.05

We must first check that the sample size is adequate.   Specifically, we need to check min(np 0 , n(1-p 0 )) = min( 3,536(0.211), 3,536(1-0.211))=min(746, 2790)=746. The sample size is more than adequate so the following formula can be used:

This is a lower tailed test, using a Z statistic and a 5% level of significance. Reject H 0 if Z < -1.645.

We reject H 0 because -10.93 < -1.645. We have statistically significant evidence at α=0.05 to show that the prevalence of smoking in the Framingham Offspring is lower than the prevalence nationally (21.1%). Here, p < 0.0001.  

The NCHS report indicated that in 2002, 75% of children aged 2 to 17 saw a dentist in the past year. An investigator wants to assess whether use of dental services is similar in children living in the city of Boston. A sample of 125 children aged 2 to 17 living in Boston are surveyed and 64 reported seeing a dentist over the past 12 months. Is there a significant difference in use of dental services between children living in Boston and the national data?

Calculate this on your own before checking the answer.

Video - Hypothesis Test for One Sample and a Dichotomous Outcome (3:55)

Tests with Two Independent Samples, Continuous Outcome

There are many applications where it is of interest to compare two independent groups with respect to their mean scores on a continuous outcome. Here we compare means between groups, but rather than generating an estimate of the difference, we will test whether the observed difference (increase, decrease or difference) is statistically significant or not. Remember, that hypothesis testing gives an assessment of statistical significance, whereas estimation gives an estimate of effect and both are important.

Here we discuss the comparison of means when the two comparison groups are independent or physically separate. The two groups might be determined by a particular attribute (e.g., sex, diagnosis of cardiovascular disease) or might be set up by the investigator (e.g., participants assigned to receive an experimental treatment or placebo). The first step in the analysis involves computing descriptive statistics on each of the two samples. Specifically, we compute the sample size, mean and standard deviation in each sample and we denote these summary statistics as follows:

for sample 1:

for sample 2:

The designation of sample 1 and sample 2 is arbitrary. In a clinical trial setting the convention is to call the treatment group 1 and the control group 2. However, when comparing men and women, for example, either group can be 1 or 2.  

In the two independent samples application with a continuous outcome, the parameter of interest in the test of hypothesis is the difference in population means, μ 1 -μ 2 . The null hypothesis is always that there is no difference between groups with respect to means, i.e.,

The null hypothesis can also be written as follows: H 0 : μ 1 = μ 2 . In the research hypothesis, an investigator can hypothesize that the first mean is larger than the second (H 1 : μ 1 > μ 2 ), that the first mean is smaller than the second (H 1 : μ 1 < μ 2 ), or that the means are different (H 1 : μ 1 ≠ μ 2 ). The three different alternatives represent upper-, lower-, and two-tailed tests, respectively. The following test statistics are used to test these hypotheses.

Test Statistics for Testing H 0 : μ 1 = μ 2

• if n 1 > 30 and n 2 > 30
• if n 1 < 30 or n 2 < 30

NOTE: The formulas above assume equal variability in the two populations (i.e., the population variances are equal, or s 1 2 = s 2 2 ). This means that the outcome is equally variable in each of the comparison populations. For analysis, we have samples from each of the comparison populations. If the sample variances are similar, then the assumption about variability in the populations is probably reasonable. As a guideline, if the ratio of the sample variances, s 1 2 /s 2 2 is between 0.5 and 2 (i.e., if one variance is no more than double the other), then the formulas above are appropriate. If the ratio of the sample variances is greater than 2 or less than 0.5 then alternative formulas must be used to account for the heterogeneity in variances.    

The test statistics include Sp, which is the pooled estimate of the common standard deviation (again assuming that the variances in the populations are similar) computed as the weighted average of the standard deviations in the samples as follows:

Because we are assuming equal variances between groups, we pool the information on variability (sample variances) to generate an estimate of the variability in the population. Note: Because Sp is a weighted average of the standard deviations in the sample, Sp will always be in between s 1 and s 2 .)

Data measured on n=3,539 participants who attended the seventh examination of the Offspring in the Framingham Heart Study are shown below.  

Suppose we now wish to assess whether there is a statistically significant difference in mean systolic blood pressures between men and women using a 5% level of significance.  

H 0 : μ 1 = μ 2

H 1 : μ 1 ≠ μ 2                       α=0.05

Because both samples are large ( > 30), we can use the Z test statistic as opposed to t. Note that statistical computing packages use t throughout. Before implementing the formula, we first check whether the assumption of equality of population variances is reasonable. The guideline suggests investigating the ratio of the sample variances, s 1 2 /s 2 2 . Suppose we call the men group 1 and the women group 2. Again, this is arbitrary; it only needs to be noted when interpreting the results. The ratio of the sample variances is 17.5 2 /20.1 2 = 0.76, which falls between 0.5 and 2 suggesting that the assumption of equality of population variances is reasonable. The appropriate test statistic is

We now substitute the sample data into the formula for the test statistic identified in Step 2. Before substituting, we will first compute Sp, the pooled estimate of the common standard deviation.

Notice that the pooled estimate of the common standard deviation, Sp, falls in between the standard deviations in the comparison groups (i.e., 17.5 and 20.1). Sp is slightly closer in value to the standard deviation in the women (20.1) as there were slightly more women in the sample.   Recall, Sp is a weight average of the standard deviations in the comparison groups, weighted by the respective sample sizes.  

Now the test statistic:

We reject H 0 because 2.66 > 1.960. We have statistically significant evidence at α=0.05 to show that there is a difference in mean systolic blood pressures between men and women. The p-value is p < 0.010.  

Here again we find that there is a statistically significant difference in mean systolic blood pressures between men and women at p < 0.010. Notice that there is a very small difference in the sample means (128.2-126.5 = 1.7 units), but this difference is beyond what would be expected by chance. Is this a clinically meaningful difference? The large sample size in this example is driving the statistical significance. A 95% confidence interval for the difference in mean systolic blood pressures is: 1.7 + 1.26 or (0.44, 2.96). The confidence interval provides an assessment of the magnitude of the difference between means whereas the test of hypothesis and p-value provide an assessment of the statistical significance of the difference.  

Above we performed a study to evaluate a new drug designed to lower total cholesterol. The study involved one sample of patients, each patient took the new drug for 6 weeks and had their cholesterol measured. As a means of evaluating the efficacy of the new drug, the mean total cholesterol following 6 weeks of treatment was compared to the NCHS-reported mean total cholesterol level in 2002 for all adults of 203. At the end of the example, we discussed the appropriateness of the fixed comparator as well as an alternative study design to evaluate the effect of the new drug involving two treatment groups, where one group receives the new drug and the other does not. Here, we revisit the example with a concurrent or parallel control group, which is very typical in randomized controlled trials or clinical trials (refer to the EP713 module on Clinical Trials).  

A new drug is proposed to lower total cholesterol. A randomized controlled trial is designed to evaluate the efficacy of the medication in lowering cholesterol. Thirty participants are enrolled in the trial and are randomly assigned to receive either the new drug or a placebo. The participants do not know which treatment they are assigned. Each participant is asked to take the assigned treatment for 6 weeks. At the end of 6 weeks, each patient's total cholesterol level is measured and the sample statistics are as follows.

Is there statistical evidence of a reduction in mean total cholesterol in patients taking the new drug for 6 weeks as compared to participants taking placebo? We will run the test using the five-step approach.

H 0 : μ 1 = μ 2 H 1 : μ 1 < μ 2                         α=0.05

Because both samples are small (< 30), we use the t test statistic. Before implementing the formula, we first check whether the assumption of equality of population variances is reasonable. The ratio of the sample variances, s 1 2 /s 2 2 =28.7 2 /30.3 2 = 0.90, which falls between 0.5 and 2, suggesting that the assumption of equality of population variances is reasonable. The appropriate test statistic is:

This is a lower-tailed test, using a t statistic and a 5% level of significance. The appropriate critical value can be found in the t Table (in More Resources to the right). In order to determine the critical value of t we need degrees of freedom, df, defined as df=n 1 +n 2 -2 = 15+15-2=28. The critical value for a lower tailed test with df=28 and α=0.05 is -1.701 and the decision rule is: Reject H 0 if t < -1.701.

Now the test statistic,

We reject H 0 because -2.92 < -1.701. We have statistically significant evidence at α=0.05 to show that the mean total cholesterol level is lower in patients taking the new drug for 6 weeks as compared to patients taking placebo, p < 0.005.

The clinical trial in this example finds a statistically significant reduction in total cholesterol, whereas in the previous example where we had a historical control (as opposed to a parallel control group) we did not demonstrate efficacy of the new drug. Notice that the mean total cholesterol level in patients taking placebo is 217.4 which is very different from the mean cholesterol reported among all Americans in 2002 of 203 and used as the comparator in the prior example. The historical control value may not have been the most appropriate comparator as cholesterol levels have been increasing over time. In the next section, we present another design that can be used to assess the efficacy of the new drug.

Video - Comparison of Two Independent Samples With a Continuous Outcome (8:02)

Tests with Matched Samples, Continuous Outcome

In the previous section we compared two groups with respect to their mean scores on a continuous outcome. An alternative study design is to compare matched or paired samples. The two comparison groups are said to be dependent, and the data can arise from a single sample of participants where each participant is measured twice (possibly before and after an intervention) or from two samples that are matched on specific characteristics (e.g., siblings). When the samples are dependent, we focus on difference scores in each participant or between members of a pair and the test of hypothesis is based on the mean difference, μ d . The null hypothesis again reflects "no difference" and is stated as H 0 : μ d =0 . Note that there are some instances where it is of interest to test whether there is a difference of a particular magnitude (e.g., μ d =5) but in most instances the null hypothesis reflects no difference (i.e., μ d =0).  

The appropriate formula for the test of hypothesis depends on the sample size. The formulas are shown below and are identical to those we presented for estimating the mean of a single sample presented (e.g., when comparing against an external or historical control), except here we focus on difference scores.

Test Statistics for Testing H 0 : μ d =0

A new drug is proposed to lower total cholesterol and a study is designed to evaluate the efficacy of the drug in lowering cholesterol. Fifteen patients agree to participate in the study and each is asked to take the new drug for 6 weeks. However, before starting the treatment, each patient's total cholesterol level is measured. The initial measurement is a pre-treatment or baseline value. After taking the drug for 6 weeks, each patient's total cholesterol level is measured again and the data are shown below. The rightmost column contains difference scores for each patient, computed by subtracting the 6 week cholesterol level from the baseline level. The differences represent the reduction in total cholesterol over 4 weeks. (The differences could have been computed by subtracting the baseline total cholesterol level from the level measured at 6 weeks. The way in which the differences are computed does not affect the outcome of the analysis only the interpretation.)

Because the differences are computed by subtracting the cholesterols measured at 6 weeks from the baseline values, positive differences indicate reductions and negative differences indicate increases (e.g., participant 12 increases by 2 units over 6 weeks). The goal here is to test whether there is a statistically significant reduction in cholesterol. Because of the way in which we computed the differences, we want to look for an increase in the mean difference (i.e., a positive reduction). In order to conduct the test, we need to summarize the differences. In this sample, we have

The calculations are shown below.  

Is there statistical evidence of a reduction in mean total cholesterol in patients after using the new medication for 6 weeks? We will run the test using the five-step approach.

H 0 : μ d = 0 H 1 : μ d > 0                 α=0.05

NOTE: If we had computed differences by subtracting the baseline level from the level measured at 6 weeks then negative differences would have reflected reductions and the research hypothesis would have been H 1 : μ d < 0. 

• Step 2 . Select the appropriate test statistic.

This is an upper-tailed test, using a t statistic and a 5% level of significance. The appropriate critical value can be found in the t Table at the right, with df=15-1=14. The critical value for an upper-tailed test with df=14 and α=0.05 is 2.145 and the decision rule is Reject H 0 if t > 2.145.

We now substitute the sample data into the formula for the test statistic identified in Step 2.

We reject H 0 because 4.61 > 2.145. We have statistically significant evidence at α=0.05 to show that there is a reduction in cholesterol levels over 6 weeks.  

Here we illustrate the use of a matched design to test the efficacy of a new drug to lower total cholesterol. We also considered a parallel design (randomized clinical trial) and a study using a historical comparator. It is extremely important to design studies that are best suited to detect a meaningful difference when one exists. There are often several alternatives and investigators work with biostatisticians to determine the best design for each application. It is worth noting that the matched design used here can be problematic in that observed differences may only reflect a "placebo" effect. All participants took the assigned medication, but is the observed reduction attributable to the medication or a result of these participation in a study.

Video - Hypothesis Testing With a Matched Sample and a Continuous Outcome (3:11)

Tests with Two Independent Samples, Dichotomous Outcome

There are several approaches that can be used to test hypotheses concerning two independent proportions. Here we present one approach - the chi-square test of independence is an alternative, equivalent, and perhaps more popular approach to the same analysis. Hypothesis testing with the chi-square test is addressed in the third module in this series: BS704_HypothesisTesting-ChiSquare.

In tests of hypothesis comparing proportions between two independent groups, one test is performed and results can be interpreted to apply to a risk difference, relative risk or odds ratio. As a reminder, the risk difference is computed by taking the difference in proportions between comparison groups, the risk ratio is computed by taking the ratio of proportions, and the odds ratio is computed by taking the ratio of the odds of success in the comparison groups. Because the null values for the risk difference, the risk ratio and the odds ratio are different, the hypotheses in tests of hypothesis look slightly different depending on which measure is used. When performing tests of hypothesis for the risk difference, relative risk or odds ratio, the convention is to label the exposed or treated group 1 and the unexposed or control group 2.      

For example, suppose a study is designed to assess whether there is a significant difference in proportions in two independent comparison groups. The test of interest is as follows:

H 0 : p 1 = p 2 versus H 1 : p 1 ≠ p 2 .  

The following are the hypothesis for testing for a difference in proportions using the risk difference, the risk ratio and the odds ratio. First, the hypotheses above are equivalent to the following:

• For the risk difference, H 0 : p 1 - p 2 = 0 versus H 1 : p 1 - p 2 ≠ 0 which are, by definition, equal to H 0 : RD = 0 versus H 1 : RD ≠ 0.
• If an investigator wants to focus on the risk ratio, the equivalent hypotheses are H 0 : RR = 1 versus H 1 : RR ≠ 1.
• If the investigator wants to focus on the odds ratio, the equivalent hypotheses are H 0 : OR = 1 versus H 1 : OR ≠ 1.  

Suppose a test is performed to test H 0 : RD = 0 versus H 1 : RD ≠ 0 and the test rejects H 0 at α=0.05. Based on this test we can conclude that there is significant evidence, α=0.05, of a difference in proportions, significant evidence that the risk difference is not zero, significant evidence that the risk ratio and odds ratio are not one. The risk difference is analogous to the difference in means when the outcome is continuous. Here the parameter of interest is the difference in proportions in the population, RD = p 1 -p 2 and the null value for the risk difference is zero. In a test of hypothesis for the risk difference, the null hypothesis is always H 0 : RD = 0. This is equivalent to H 0 : RR = 1 and H 0 : OR = 1. In the research hypothesis, an investigator can hypothesize that the first proportion is larger than the second (H 1 : p 1 > p 2 , which is equivalent to H 1 : RD > 0, H 1 : RR > 1 and H 1 : OR > 1), that the first proportion is smaller than the second (H 1 : p 1 < p 2 , which is equivalent to H 1 : RD < 0, H 1 : RR < 1 and H 1 : OR < 1), or that the proportions are different (H 1 : p 1 ≠ p 2 , which is equivalent to H 1 : RD ≠ 0, H 1 : RR ≠ 1 and H 1 : OR ≠

1). The three different alternatives represent upper-, lower- and two-tailed tests, respectively.  

The formula for the test of hypothesis for the difference in proportions is given below.

Test Statistics for Testing H 0 : p 1 = p

The formula above is appropriate for large samples, defined as at least 5 successes (np > 5) and at least 5 failures (n(1-p > 5)) in each of the two samples. If there are fewer than 5 successes or failures in either comparison group, then alternative procedures, called exact methods must be used to estimate the difference in population proportions.

The following table summarizes data from n=3,799 participants who attended the fifth examination of the Offspring in the Framingham Heart Study. The outcome of interest is prevalent CVD and we want to test whether the prevalence of CVD is significantly higher in smokers as compared to non-smokers.

The prevalence of CVD (or proportion of participants with prevalent CVD) among non-smokers is 298/3,055 = 0.0975 and the prevalence of CVD among current smokers is 81/744 = 0.1089. Here smoking status defines the comparison groups and we will call the current smokers group 1 (exposed) and the non-smokers (unexposed) group 2. The test of hypothesis is conducted below using the five step approach.

H 0 : p 1 = p 2     H 1 : p 1 ≠ p 2                 α=0.05

• Step 2.  Select the appropriate test statistic.  

We must first check that the sample size is adequate. Specifically, we need to ensure that we have at least 5 successes and 5 failures in each comparison group. In this example, we have more than enough successes (cases of prevalent CVD) and failures (persons free of CVD) in each comparison group. The sample size is more than adequate so the following formula can be used:

Reject H 0 if Z < -1.960 or if Z > 1.960.

We now substitute the sample data into the formula for the test statistic identified in Step 2. We first compute the overall proportion of successes:

We now substitute to compute the test statistic.

• Step 5. Conclusion.

We do not reject H 0 because -1.960 < 0.927 < 1.960. We do not have statistically significant evidence at α=0.05 to show that there is a difference in prevalent CVD between smokers and non-smokers.  

A 95% confidence interval for the difference in prevalent CVD (or risk difference) between smokers and non-smokers as 0.0114 + 0.0247, or between -0.0133 and 0.0361. Because the 95% confidence interval for the risk difference includes zero we again conclude that there is no statistically significant difference in prevalent CVD between smokers and non-smokers.    

Smoking has been shown over and over to be a risk factor for cardiovascular disease. What might explain the fact that we did not observe a statistically significant difference using data from the Framingham Heart Study? HINT: Here we consider prevalent CVD, would the results have been different if we considered incident CVD?

A randomized trial is designed to evaluate the effectiveness of a newly developed pain reliever designed to reduce pain in patients following joint replacement surgery. The trial compares the new pain reliever to the pain reliever currently in use (called the standard of care). A total of 100 patients undergoing joint replacement surgery agreed to participate in the trial. Patients were randomly assigned to receive either the new pain reliever or the standard pain reliever following surgery and were blind to the treatment assignment. Before receiving the assigned treatment, patients were asked to rate their pain on a scale of 0-10 with higher scores indicative of more pain. Each patient was then given the assigned treatment and after 30 minutes was again asked to rate their pain on the same scale. The primary outcome was a reduction in pain of 3 or more scale points (defined by clinicians as a clinically meaningful reduction). The following data were observed in the trial.

We now test whether there is a statistically significant difference in the proportions of patients reporting a meaningful reduction (i.e., a reduction of 3 or more scale points) using the five step approach.  

H 0 : p 1 = p 2     H 1 : p 1 ≠ p 2              α=0.05

Here the new or experimental pain reliever is group 1 and the standard pain reliever is group 2.

We must first check that the sample size is adequate. Specifically, we need to ensure that we have at least 5 successes and 5 failures in each comparison group, i.e.,

In this example, we have min(50(0.46), 50(1-0.46), 50(0.22), 50(1-0.22)) = min(23, 27, 11, 39) = 11. The sample size is adequate so the following formula can be used

We reject H 0 because 2.526 > 1960. We have statistically significant evidence at a =0.05 to show that there is a difference in the proportions of patients on the new pain reliever reporting a meaningful reduction (i.e., a reduction of 3 or more scale points) as compared to patients on the standard pain reliever.

A 95% confidence interval for the difference in proportions of patients on the new pain reliever reporting a meaningful reduction (i.e., a reduction of 3 or more scale points) as compared to patients on the standard pain reliever is 0.24 + 0.18 or between 0.06 and 0.42. Because the 95% confidence interval does not include zero we concluded that there was a statistically significant difference in proportions which is consistent with the test of hypothesis result. 

Again, the procedures discussed here apply to applications where there are two independent comparison groups and a dichotomous outcome. There are other applications in which it is of interest to compare a dichotomous outcome in matched or paired samples. For example, in a clinical trial we might wish to test the effectiveness of a new antibiotic eye drop for the treatment of bacterial conjunctivitis. Participants use the new antibiotic eye drop in one eye and a comparator (placebo or active control treatment) in the other. The success of the treatment (yes/no) is recorded for each participant for each eye. Because the two assessments (success or failure) are paired, we cannot use the procedures discussed here. The appropriate test is called McNemar's test (sometimes called McNemar's test for dependent proportions).  

Vide0 - Hypothesis Testing With Two Independent Samples and a Dichotomous Outcome (2:55)

Here we presented hypothesis testing techniques for means and proportions in one and two sample situations. Tests of hypothesis involve several steps, including specifying the null and alternative or research hypothesis, selecting and computing an appropriate test statistic, setting up a decision rule and drawing a conclusion. There are many details to consider in hypothesis testing. The first is to determine the appropriate test. We discussed Z and t tests here for different applications. The appropriate test depends on the distribution of the outcome variable (continuous or dichotomous), the number of comparison groups (one, two) and whether the comparison groups are independent or dependent. The following table summarizes the different tests of hypothesis discussed here.

• Continuous Outcome, One Sample: H0: μ = μ0
• Continuous Outcome, Two Independent Samples: H0: μ1 = μ2
• Continuous Outcome, Two Matched Samples: H0: μd = 0
• Dichotomous Outcome, One Sample: H0: p = p 0
• Dichotomous Outcome, Two Independent Samples: H0: p1 = p2, RD=0, RR=1, OR=1

Once the type of test is determined, the details of the test must be specified. Specifically, the null and alternative hypotheses must be clearly stated. The null hypothesis always reflects the "no change" or "no difference" situation. The alternative or research hypothesis reflects the investigator's belief. The investigator might hypothesize that a parameter (e.g., a mean, proportion, difference in means or proportions) will increase, will decrease or will be different under specific conditions (sometimes the conditions are different experimental conditions and other times the conditions are simply different groups of participants). Once the hypotheses are specified, data are collected and summarized. The appropriate test is then conducted according to the five step approach. If the test leads to rejection of the null hypothesis, an approximate p-value is computed to summarize the significance of the findings. When tests of hypothesis are conducted using statistical computing packages, exact p-values are computed. Because the statistical tables in this textbook are limited, we can only approximate p-values. If the test fails to reject the null hypothesis, then a weaker concluding statement is made for the following reason.

In hypothesis testing, there are two types of errors that can be committed. A Type I error occurs when a test incorrectly rejects the null hypothesis. This is referred to as a false positive result, and the probability that this occurs is equal to the level of significance, α. The investigator chooses the level of significance in Step 1, and purposely chooses a small value such as α=0.05 to control the probability of committing a Type I error. A Type II error occurs when a test fails to reject the null hypothesis when in fact it is false. The probability that this occurs is equal to β. Unfortunately, the investigator cannot specify β at the outset because it depends on several factors including the sample size (smaller samples have higher b), the level of significance (β decreases as a increases), and the difference in the parameter under the null and alternative hypothesis.    

We noted in several examples in this chapter, the relationship between confidence intervals and tests of hypothesis. The approaches are different, yet related. It is possible to draw a conclusion about statistical significance by examining a confidence interval. For example, if a 95% confidence interval does not contain the null value (e.g., zero when analyzing a mean difference or risk difference, one when analyzing relative risks or odds ratios), then one can conclude that a two-sided test of hypothesis would reject the null at α=0.05. It is important to note that the correspondence between a confidence interval and test of hypothesis relates to a two-sided test and that the confidence level corresponds to a specific level of significance (e.g., 95% to α=0.05, 90% to α=0.10 and so on). The exact significance of the test, the p-value, can only be determined using the hypothesis testing approach and the p-value provides an assessment of the strength of the evidence and not an estimate of the effect.

Answers to Selected Problems

Dental services problem - bottom of page 5.

• Step 1: Set up hypotheses and determine the level of significance.

α=0.05

• Step 2: Select the appropriate test statistic.

First, determine whether the sample size is adequate.

Therefore the sample size is adequate, and we can use the following formula:

• Step 3: Set up the decision rule.

Reject H0 if Z is less than or equal to -1.96 or if Z is greater than or equal to 1.96.

• Step 4: Compute the test statistic
• Step 5: Conclusion.

We reject the null hypothesis because -6.15<-1.96. Therefore there is a statistically significant difference in the proportion of children in Boston using dental services compated to the national proportion.

User Preferences

Content preview.

Arcu felis bibendum ut tristique et egestas quis:

• Ut enim ad minim veniam, quis nostrud exercitation ullamco laboris
• Duis aute irure dolor in reprehenderit in voluptate
• Excepteur sint occaecat cupidatat non proident

Keyboard Shortcuts

5.5 - hypothesis testing for two-sample proportions.

We are now going to develop the hypothesis test for the difference of two proportions for independent samples. The hypothesis test follows the same steps as one group.

These notes are going to go into a little bit of math and formulas to help demonstrate the logic behind hypothesis testing for two groups. If this starts to get a little confusion, just skim over it for a general understanding! Remember we can rely on the software to do the calculations for us, but it is good to have a basic understanding of the logic!

We will use the sampling distribution of \(\hat{p}_1-\hat{p}_2\) as we did for the confidence interval.

For a test for two proportions, we are interested in the difference between two groups. If the difference is zero, then they are not different (i.e., they are equal). Therefore, the null hypothesis will always be:

\(H_0\colon p_1-p_2=0\)

Another way to look at it is \(H_0\colon p_1=p_2\). This is worth stopping to think about. Remember, in hypothesis testing, we assume the null hypothesis is true. In this case, it means that \(p_1\) and \(p_2\) are equal. Under this assumption, then \(\hat{p}_1\) and \(\hat{p}_2\) are both estimating the same proportion. Think of this proportion as \(p^*\).

Therefore, the sampling distribution of both proportions, \(\hat{p}_1\) and \(\hat{p}_2\), will, under certain conditions, be approximately normal centered around \(p^*\), with standard error \(\sqrt{\dfrac{p^*(1-p^*)}{n_i}}\), for \(i=1, 2\).

We take this into account by finding an estimate for this \(p^*\) using the two-sample proportions. We can calculate an estimate of \(p^*\) using the following formula:

\(\hat{p}^*=\dfrac{x_1+x_2}{n_1+n_2}\)

This value is the total number in the desired categories \((x_1+x_2)\) from both samples over the total number of sampling units in the combined sample \((n_1+n_2)\).

Putting everything together, if we assume \(p_1=p_2\), then the sampling distribution of \(\hat{p}_1-\hat{p}_2\) will be approximately normal with mean 0 and standard error of \(\sqrt{p^*(1-p^*)\left(\frac{1}{n_1}+\frac{1}{n_2}\right)}\), under certain conditions.

\(z^*=\dfrac{(\hat{p}_1-\hat{p}_2)-0}{\sqrt{\hat{p}^*(1-\hat{p}^*)\left(\dfrac{1}{n_1}+\dfrac{1}{n_2}\right)}}\)

...will follow a standard normal distribution.

Finally, we can develop our hypothesis test for \(p_1-p_2\).

Hypothesis Testing for Two-Sample Proportions

Conditions :

\(n_1\hat{p}_1\), \(n_1(1-\hat{p}_1)\), \(n_2\hat{p}_2\), and \(n_2(1-\hat{p}_2)\) are all greater than five

Test Statistic:

\(z^*=\dfrac{\hat{p}_1-\hat{p}_2-0}{\sqrt{\hat{p}^*(1-\hat{p}^*)\left(\dfrac{1}{n_1}+\dfrac{1}{n_2}\right)}}\)

...where \(\hat{p}^*=\dfrac{x_1+x_2}{n_1+n_2}\).

The critical values, p-values, and decisions will all follow the same steps as those from a hypothesis test for a one-sample proportion.

Have a language expert improve your writing

Run a free plagiarism check in 10 minutes, generate accurate citations for free.

• Knowledge Base

Hypothesis Testing | A Step-by-Step Guide with Easy Examples

Published on November 8, 2019 by Rebecca Bevans . Revised on June 22, 2023.

Hypothesis testing is a formal procedure for investigating our ideas about the world using statistics . It is most often used by scientists to test specific predictions, called hypotheses, that arise from theories.

There are 5 main steps in hypothesis testing:

• State your research hypothesis as a null hypothesis and alternate hypothesis (H o ) and (H a  or H 1 ).
• Collect data in a way designed to test the hypothesis.
• Perform an appropriate statistical test .
• Decide whether to reject or fail to reject your null hypothesis.
• Present the findings in your results and discussion section.

Though the specific details might vary, the procedure you will use when testing a hypothesis will always follow some version of these steps.

Table of contents

Step 1: state your null and alternate hypothesis, step 2: collect data, step 3: perform a statistical test, step 4: decide whether to reject or fail to reject your null hypothesis, step 5: present your findings, other interesting articles, frequently asked questions about hypothesis testing.

After developing your initial research hypothesis (the prediction that you want to investigate), it is important to restate it as a null (H o ) and alternate (H a ) hypothesis so that you can test it mathematically.

The alternate hypothesis is usually your initial hypothesis that predicts a relationship between variables. The null hypothesis is a prediction of no relationship between the variables you are interested in.

• H 0 : Men are, on average, not taller than women. H a : Men are, on average, taller than women.

Here's why students love Scribbr's proofreading services

Discover proofreading & editing

For a statistical test to be valid , it is important to perform sampling and collect data in a way that is designed to test your hypothesis. If your data are not representative, then you cannot make statistical inferences about the population you are interested in.

There are a variety of statistical tests available, but they are all based on the comparison of within-group variance (how spread out the data is within a category) versus between-group variance (how different the categories are from one another).

If the between-group variance is large enough that there is little or no overlap between groups, then your statistical test will reflect that by showing a low p -value . This means it is unlikely that the differences between these groups came about by chance.

Alternatively, if there is high within-group variance and low between-group variance, then your statistical test will reflect that with a high p -value. This means it is likely that any difference you measure between groups is due to chance.

Your choice of statistical test will be based on the type of variables and the level of measurement of your collected data .

• an estimate of the difference in average height between the two groups.
• a p -value showing how likely you are to see this difference if the null hypothesis of no difference is true.

Based on the outcome of your statistical test, you will have to decide whether to reject or fail to reject your null hypothesis.

In most cases you will use the p -value generated by your statistical test to guide your decision. And in most cases, your predetermined level of significance for rejecting the null hypothesis will be 0.05 – that is, when there is a less than 5% chance that you would see these results if the null hypothesis were true.

In some cases, researchers choose a more conservative level of significance, such as 0.01 (1%). This minimizes the risk of incorrectly rejecting the null hypothesis ( Type I error ).

Receive feedback on language, structure, and formatting

Professional editors proofread and edit your paper by focusing on:

• Academic style
• Vague sentences
• Style consistency

See an example

The results of hypothesis testing will be presented in the results and discussion sections of your research paper , dissertation or thesis .

In the results section you should give a brief summary of the data and a summary of the results of your statistical test (for example, the estimated difference between group means and associated p -value). In the discussion , you can discuss whether your initial hypothesis was supported by your results or not.

In the formal language of hypothesis testing, we talk about rejecting or failing to reject the null hypothesis. You will probably be asked to do this in your statistics assignments.

However, when presenting research results in academic papers we rarely talk this way. Instead, we go back to our alternate hypothesis (in this case, the hypothesis that men are on average taller than women) and state whether the result of our test did or did not support the alternate hypothesis.

If your null hypothesis was rejected, this result is interpreted as “supported the alternate hypothesis.”

These are superficial differences; you can see that they mean the same thing.

You might notice that we don’t say that we reject or fail to reject the alternate hypothesis . This is because hypothesis testing is not designed to prove or disprove anything. It is only designed to test whether a pattern we measure could have arisen spuriously, or by chance.

If we reject the null hypothesis based on our research (i.e., we find that it is unlikely that the pattern arose by chance), then we can say our test lends support to our hypothesis . But if the pattern does not pass our decision rule, meaning that it could have arisen by chance, then we say the test is inconsistent with our hypothesis .

If you want to know more about statistics , methodology , or research bias , make sure to check out some of our other articles with explanations and examples.

• Normal distribution
• Descriptive statistics
• Measures of central tendency
• Correlation coefficient

Methodology

• Cluster sampling
• Stratified sampling
• Types of interviews
• Cohort study
• Thematic analysis

Research bias

• Implicit bias
• Cognitive bias
• Survivorship bias
• Availability heuristic
• Nonresponse bias
• Regression to the mean

Hypothesis testing is a formal procedure for investigating our ideas about the world using statistics. It is used by scientists to test specific predictions, called hypotheses , by calculating how likely it is that a pattern or relationship between variables could have arisen by chance.

A hypothesis states your predictions about what your research will find. It is a tentative answer to your research question that has not yet been tested. For some research projects, you might have to write several hypotheses that address different aspects of your research question.

A hypothesis is not just a guess — it should be based on existing theories and knowledge. It also has to be testable, which means you can support or refute it through scientific research methods (such as experiments, observations and statistical analysis of data).

Null and alternative hypotheses are used in statistical hypothesis testing . The null hypothesis of a test always predicts no effect or no relationship between variables, while the alternative hypothesis states your research prediction of an effect or relationship.

Cite this Scribbr article

If you want to cite this source, you can copy and paste the citation or click the “Cite this Scribbr article” button to automatically add the citation to our free Citation Generator.

Bevans, R. (2023, June 22). Hypothesis Testing | A Step-by-Step Guide with Easy Examples. Scribbr. Retrieved April 1, 2024, from https://www.scribbr.com/statistics/hypothesis-testing/

Is this article helpful?

Rebecca Bevans

Other students also liked, choosing the right statistical test | types & examples, understanding p values | definition and examples, what is your plagiarism score.

Want to create or adapt books like this? Learn more about how Pressbooks supports open publishing practices.

8.8 Hypothesis Tests for a Population Proportion

Learning objectives.

• Conduct and interpret hypothesis tests for a population proportion.

Some notes about conducting a hypothesis test:

• The null hypothesis [latex]H_0[/latex] is always an “equal to.”  The null hypothesis is the original claim about the population parameter.
• The alternative hypothesis [latex]H_a[/latex] is a “less than,” “greater than,” or “not equal to.”  The form of the alternative hypothesis depends on the context of the question.
• If the alternative hypothesis is a “less than”, then the test is left-tail.  The p -value is the area in the left-tail of the distribution.
• If the alternative hypothesis is a “greater than”, then the test is right-tail.  The p -value is the area in the right-tail of the distribution.
• If the alternative hypothesis is a “not equal to”, then the test is two-tail.  The p -value is the sum of the area in the two-tails of the distribution.  Each tail represents exactly half of the p -value.
• Think about the meaning of the p -value.  A data analyst (and anyone else) should have more confidence that they made the correct decision to reject the null hypothesis with a smaller p -value (for example, 0.001 as opposed to 0.04) even if using a significance level of 0.05. Similarly, for a large p -value such as 0.4, as opposed to a p -value of 0.056 (a significance level of 0.05 is less than either number), a data analyst should have more confidence that they made the correct decision in not rejecting the null hypothesis. This makes the data analyst use judgment rather than mindlessly applying rules.
• The significance level must be identified before collecting the sample data and conducting the test.  Generally, the significance level will be included in the question.  If no significance level is given, a common standard is to use a significance level of 5%.

Suppose the hypotheses for a hypothesis test are:

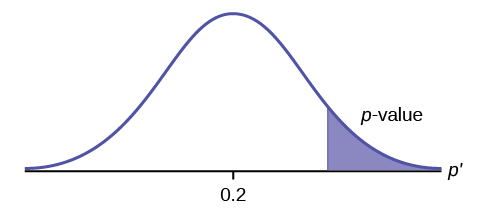
[latex]\begin{eqnarray*} H_0: & & p=20 \% \\ H_a: & & p \gt 20\% \end{eqnarray*}[/latex]

Because the alternative hypothesis is a [latex]\gt[/latex], this is a right-tail test.  The p -value is the area in the right-tail of the distribution.

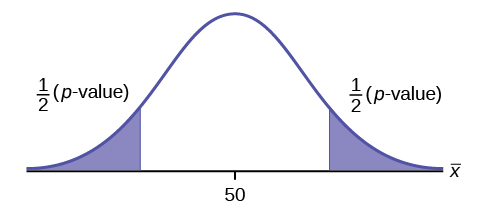
[latex]\begin{eqnarray*} H_0: & & p=50 \% \\ H_a: & & p \neq  50\% \end{eqnarray*}[/latex]

Because the alternative hypothesis is a [latex]\neq[/latex], this is a two-tail test.  The p -value is the sum of the areas in the two tails of the distribution.  Each tail contains exactly half of the p -value.

[latex]\begin{eqnarray*} H_0: & & p=10\% \\ H_a: & & p \lt  10\% \end{eqnarray*}[/latex]

Because the alternative hypothesis is a [latex]\lt[/latex], this is a left-tail test.  The p -value is the area in the left-tail of the distribution.

Steps to Conduct a Hypothesis Test for a Population Proportion

• Write down the null and alternative hypotheses in terms of the population proportion [latex]p[/latex].  Include appropriate units with the values of the proportion.
• Use the form of the alternative hypothesis to determine if the test is left-tailed, right-tailed, or two-tailed.
• Collect the sample information for the test and identify the significance level.
• If [latex]n \times p \geq 5[/latex] and [latex]n \times (1-p) \geq 5[/latex], use the normal distribution with [latex]\displaystyle{z=\frac{\hat{p}-p}{\sqrt{\frac{p \times (1-p)}{n}}}}[/latex].
• If one of [latex]n \times p \lt 5[/latex] or [latex]n \times (1-p) \lt 5[/latex], use a binomial distribution.
• The results of the sample data are significant.  There is sufficient evidence to conclude that the null hypothesis [latex]H_0[/latex] is an incorrect belief and that the alternative hypothesis [latex]H_a[/latex] is most likely correct.
• The results of the sample data are not significant.  There is not sufficient evidence to conclude that the alternative hypothesis [latex]H_a[/latex] may be correct.
• Write down a concluding sentence specific to the context of the question.

USING EXCEL TO CALCULE THE P -VALUE FOR A HYPOTHESIS TEST ON A POPULATION PROPORTION

The p -value for a hypothesis test on a population proportion is the area in the tail(s) of distribution of the sample proportion.  If both [latex]n \times p \geq 5[/latex] and [latex]n \times (1-p) \geq 5[/latex], use the normal distribution to find the p -value.  If at least one of [latex]n \times p \lt 5[/latex] or [latex]n \times (1-p) \lt 5[/latex], use the binomial distribution to find the p -value.

If both [latex]n \times p \geq 5[/latex] and [latex]n \times (1-p) \geq 5[/latex]:

• For x , enter the value for [latex]\hat{p}[/latex].
• For [latex]\mu[/latex] , enter the mean of the sample proportions [latex]p[/latex].  Note:  Because the test is run assuming the null hypothesis is true, the value for [latex]p[/latex] is the claim from the null hypothesis.
• For [latex]\sigma[/latex] , enter the standard error of the proportions [latex]\displaystyle{\sqrt{\frac{p \times (1-p)}{n}}}[/latex].
• For the logic operator , enter true .  Note:  Because we are calculating the area under the curve, we always enter true for the logic operator.
• Use the appropriate technique with the norm.dist function to find the area in the left-tail or the area in the right-tail.

If at least one of [latex]n \times p \lt 5[/latex] or [latex]n \times (1-p) \lt 5[/latex]:

• The p -value is found using the binomial distribution.
• For x , enter the number of successes.
• For n , enter the sample size.
• For p , enter the the value of the population proportion [latex]p[/latex] from the null hypothesis.
• For the logic operator , enter true .  Note:  Because we are calculating an at most probability, the logic operator is always true.
• For p , enter the the value of the population proportion [latex]p[/latex] in the null hypothesis.
• For the logic operator , enter true .  Note:  Because we are calculating an at least probability, the logic operator is always true.

Marketers believe that 92% of adults own a cell phone.  A cell phone manufacturer believes that number is actually lower.  In a sample of 200 adults, 87% own a cell phone.  At the 1% significance level, determine if the proportion of adults that own a cell phone is lower than the marketers’ claim.

Hypotheses:

[latex]\begin{eqnarray*} H_0: & & p=92\% \mbox{ of adults own a cell phone} \\ H_a: & & p \lt 92\% \mbox{ of adults own a cell phone} \end{eqnarray*}[/latex]

From the question, we have [latex]n=200[/latex], [latex]\hat{p}=0.87[/latex], and [latex]\alpha=0.01[/latex].

To determine the distribution, we check [latex]n \times p[/latex] and [latex]n \times (1-p)[/latex].  For the value of [latex]p[/latex], we use the claim from the null hypothesis ([latex]p=0.92[/latex]).

[latex]\begin{eqnarray*} n \times p & = & 200 \times 0.92=184 \geq 5 \\ n \times (1-p) & = & 200 \times (1-0.92)=16 \geq 5\end{eqnarray*}[/latex]

Because both [latex]n \times p \geq 5[/latex] and [latex]n \times (1-p)  \geq 5[/latex] we use a normal distribution to calculate the p -value.  Because the alternative hypothesis is a [latex]\lt[/latex], the p -value is the area in the left tail of the distribution.

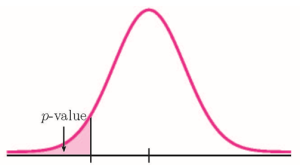
So the p -value[latex]=0.0046[/latex].

Conclusion:

Because p -value[latex]=0.0046 \lt 0.01=\alpha[/latex], we reject the null hypothesis in favour of the alternative hypothesis.  At the 1% significance level there is enough evidence to suggest that the proportion of adults who own a cell phone is lower than 92%.

• The null hypothesis [latex]p=92\%[/latex] is the claim that 92% of adults own a cell phone.
• The alternative hypothesis [latex]p \lt 92\%[/latex] is the claim that less than 92% of adults own a cell phone.
• The function is norm.dist because we are finding the area in the left tail of a normal distribution.
• Field 1 is the value of [latex]\hat{p}[/latex].
• Field 2 is the value of [latex]p[/latex] from the null hypothesis.  Remember, we run the test assuming the null hypothesis is true, so that means we assume [latex]p=0.92[/latex].
• Field 3 is the standard deviation for the sample proportions [latex]\displaystyle{\sqrt{\frac{p \times (1-p)}{n}}}[/latex].
• The p -value of 0.0046 tells us that under the assumption that 92% of adults own a cell phone (the null hypothesis), there is only a 0.46% chance that the proportion of adults who own a cell phone in a sample of 200 is 87% or less.  This is a small probability, and so is unlikely to happen assuming the null hypothesis is true.  This suggests that the assumption that the null hypothesis is true is most likely incorrect, and so the conclusion of the test is to reject the null hypothesis in favour of the alternative hypothesis.  In other words, the proportion of adults who own a cell phone is most likely less than 92%.

A consumer group claims that the proportion of households that have at least three cell phones is 30%.  A cell phone company has reason to believe that the proportion of households with at least three cell phones is much higher.  Before they start a big advertising campaign based on the proportion of households that have at least three cell phones, they want to test their claim.  Their marketing people survey 150 households with the result that 54 of the households have at least three cell phones.  At the 1% significance level, determine if the proportion of households that have at least three cell phones is less than 30%.

[latex]\begin{eqnarray*} H_0: & & p=30\% \mbox{ of household have at least 3 cell phones} \\ H_a: & & p \gt 30\% \mbox{ of household have at least 3 cell phones} \end{eqnarray*}[/latex]

From the question, we have [latex]n=150[/latex], [latex]\displaystyle{\hat{p}=\frac{54}{150}=0.36}[/latex], and [latex]\alpha=0.01[/latex].

To determine the distribution, we check [latex]n \times p[/latex] and [latex]n \times (1-p)[/latex].  For the value of [latex]p[/latex], we use the claim from the null hypothesis ([latex]p=0.3[/latex]).

[latex]\begin{eqnarray*} n \times p & = & 150 \times 0.3=45 \geq 5 \\ n \times (1-p) & = & 150 \times (1-0.3)=105 \geq 5\end{eqnarray*}[/latex]

Because both [latex]n \times p \geq 5[/latex] and [latex]n \times (1-p)  \geq  5[/latex] we use a normal distribution to calculate the p -value.  Because the alternative hypothesis is a [latex]\gt[/latex], the p -value is the area in the right tail of the distribution.

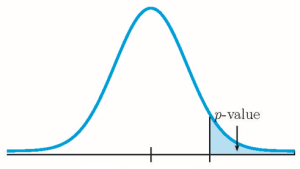
So the p -value[latex]=0.0544[/latex].

Because p -value[latex]=0.0544 \gt 0.01=\alpha[/latex], we do not reject the null hypothesis.  At the 1% significance level there is not enough evidence to suggest that the proportion of households with at least three cell phones is more than 30%.

• The null hypothesis [latex]p=30\%[/latex] is the claim that 30% of households have at least three cell phones.
• The alternative hypothesis [latex]p \gt 30\%[/latex] is the claim that more than 30% of households have at least three cell phones.
• The function is 1-norm.dist because we are finding the area in the right tail of a normal distribution.
• Field 2 is the value of [latex]p[/latex] from the null hypothesis.  Remember, we run the test assuming the null hypothesis is true, so that means we assume [latex]p=0.3[/latex].
• The p -value of 0.0544 tells us that under the assumption that 30% of households have at least three cell phones (the null hypothesis), there is a 5.44% chance that the proportion of households with at least three cell phones in a sample of 150 is 36% or more.  Compared to the 1% significance level, this is a large probability, and so is likely to happen assuming the null hypothesis is true.  This suggests that the assumption that the null hypothesis is true is most likely correct, and so the conclusion of the test is to not reject the null hypothesis.  In other words, the claim that 30% of households have at least three cell phones is most likely correct.

A teacher believes that 70% of students in the class will want to go on a field trip to the local zoo.  The students in the class believe the proportion is much higher and ask the teacher to verify her claim.  The teacher samples 50 students and 39 reply that they would want to go to the zoo.  At the 5% significance level, determine if the proportion of students who want to go on the field trip is higher than 70%.

[latex]\begin{eqnarray*} H_0: & & p = 70\% \mbox{ of students want to go on the field trip}  \\ H_a: & & p \gt 70\% \mbox{ of students want to go on the field trip}   \end{eqnarray*}[/latex]

From the question, we have [latex]n=50[/latex], [latex]\displaystyle{\hat{p}=\frac{39}{50}=0.78}[/latex], and [latex]\alpha=0.05[/latex].

[latex]\begin{eqnarray*} n \times p & = & 50 \times 0.7=35 \geq 5 \\ n \times (1-p) & = & 50 \times (1-0.7)=15 \geq 5\end{eqnarray*}[/latex]

Because both [latex]n \times p \geq 5[/latex] and [latex]n \times (1-p)  \geq 5[/latex] we use a normal distribution to calculate the p -value.  Because the alternative hypothesis is a [latex]\gt[/latex], the p -value is the area in the right tail of the distribution.

So the p -value[latex]=0.1085[/latex].

Because p -value[latex]=0.1085 \gt 0.05=\alpha[/latex], we do not reject the null hypothesis.  At the 5% significance level there is not enough evidence to suggest that the proportion of students who want to go on the field trip is higher than 70%.

• The null hypothesis [latex]p=70\%[/latex] is the claim that 70% of the students want to go on the field trip.
• The alternative hypothesis [latex]p \gt 70\%[/latex] is the claim that more than 70% of students want to go on the field trip.
• The p -value of 0.1085 tells us that under the assumption that 70% of students want to go on the field trip (the null hypothesis), there is a 10.85% chance that the proportion of students who want to go on the field trip in a sample of 50 students is 78% or more.  Compared to the 5% significance level, this is a large probability, and so is likely to happen assuming the null hypothesis is true.  This suggests that the assumption that the null hypothesis is true is most likely correct, and so the conclusion of the test is to not reject the null hypothesis.  In other words, the teacher’s claim that 70% of students want to go on the field trip is most likely correct.

Joan believes that 50% of first-time brides in the United States are younger than their grooms.  She performs a hypothesis test to determine if the percentage is the same or different from 50%.  Joan samples 100 first-time brides and 56 reply that they are younger than their grooms.  Use a 5% significance level.

[latex]\begin{eqnarray*} H_0: & & p=50\% \mbox{ of first-time brides are younger than the groom} \\ H_a: & & p \neq 50\% \mbox{ of first-time brides are younger than the groom} \end{eqnarray*}[/latex]

From the question, we have [latex]n=100[/latex], [latex]\displaystyle{\hat{p}=\frac{56}{100}=0.56}[/latex], and [latex]\alpha=0.05[/latex].

To determine the distribution, we check [latex]n \times p[/latex] and [latex]n \times (1-p)[/latex].  For the value of [latex]p[/latex], we use the claim from the null hypothesis ([latex]p=0.5[/latex]).

[latex]\begin{eqnarray*} n \times p & = & 100 \times 0.5=50 \geq 5 \\ n \times (1-p) & = & 100 \times (1-0.5)=50 \geq 5\end{eqnarray*}[/latex]

Because both [latex]n \times p \geq 5[/latex] and [latex]n \times (1-p)  \geq 5[/latex] we use a normal distribution to calculate the p -value.  Because the alternative hypothesis is a [latex]\neq[/latex], the p -value is the sum of area in the tails of the distribution.

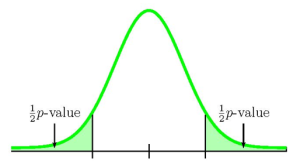
Because there is only one sample, we only have information relating to one of the two tails, either the left or the right.  We need to know if the sample relates to the left or right tail because that will determine how we calculate out the area of that tail using the normal distribution.  In this case, the sample proportion [latex]\hat{p}=0.56[/latex] is greater than the value of the population proportion in the null hypothesis [latex]p=0.5[/latex] ([latex]\hat{p}=0.56>0.5=p[/latex]), so the sample information relates to the right-tail of the normal distribution.  This means that we will calculate out the area in the right tail using 1-norm.dist .  However, this is a two-tailed test where the p -value is the sum of the area in the two tails and the area in the right-tail is only one half of the p -value.  The area in the left tail equals the area in the right tail and the p -value is the sum of these two areas.

So the area in the right tail is 0.1151 and  [latex]\frac{1}{2}[/latex]( p -value)[latex]=0.1151[/latex].  This is also the area in the left tail, so

p -value[latex]=0.1151+0.1151=0.2302[/latex]

Because p -value[latex]=0.2302 \gt 0.05=\alpha[/latex], we do not reject the null hypothesis.  At the 5% significance level there is not enough evidence to suggest that the proportion of first-time brides that are younger than the groom is different from 50%.

• The null hypothesis [latex]p=50\%[/latex] is the claim that the proportion of first-time brides that are younger than the groom is 50%.
• The alternative hypothesis [latex]p \neq 50\%[/latex] is the claim that the proportion of first-time brides that are younger than the groom is different from 50%.
• We use norm.dist([latex]\hat{p}[/latex],[latex]p[/latex],[latex]\mbox{sqrt}(p*(1-p)/n)[/latex],true) to find the area in the left tail.  The area in the right tail equals the area in the left tail, so we can find the p -value by adding the output from this function to itself.
• We use 1-norm.dist([latex]\hat{p}[/latex],[latex]p[/latex],[latex]\mbox{sqrt}(p*(1-p)/n)[/latex],true) to find the area in the right tail.  The area in the left tail equals the area in the right tail, so we can find the p -value by adding the output from this function to itself.
• The p -value of 0.2302  is a large probability compared to the 5% significance level, and so is likely to happen assuming the null hypothesis is true.  This suggests that the assumption that the null hypothesis is true is most likely correct, and so the conclusion of the test is to not reject the null hypothesis.  In other words, the claim that the proportion of first-time brides who are younger than the groom is most likely correct.

Watch this video: Hypothesis Testing for Proportions: z -test by ExcelIsFun [7:27] 

An online retailer believes that 93% of the visitors to its website will make a purchase.   A researcher in the marketing department thinks the actual percent is lower than claimed.  The researcher examines a sample of 50 visits to the website and finds that 45 of the visits resulted in a purchase.  At the 1% significance level, determine if the proportion of visits to the website that result in a purchase is lower than claimed.

[latex]\begin{eqnarray*} H_0: & & p=93\% \mbox{ of visitors make a purchase} \\ H_a: & & p \lt 93\% \mbox{ of visitors make a purchase} \end{eqnarray*}[/latex]

From the question, we have [latex]n=50[/latex], [latex]x=45[/latex], and [latex]\alpha=0.01[/latex].

To determine the distribution, we check [latex]n \times p[/latex] and [latex]n \times (1-p)[/latex].  For the value of [latex]p[/latex], we use the claim from the null hypothesis ([latex]p=0.93[/latex]).

[latex]\begin{eqnarray*} n \times p & = & 50 \times 0.93=46.5 \geq 5 \\ n \times (1-p) & = & 50 \times (1-0.93)=3.5 \lt 5\end{eqnarray*}[/latex]

Because [latex]n \times (1-p)  \lt 5[/latex] we use a binomial distribution to calculate the p -value.  Because the alternative hypothesis is a [latex]\lt[/latex], the p -value is the probability of getting at most 45 successes in 50 trials.

So the p -value[latex]=0.2710[/latex].

Because p -value[latex]=0.2710 \gt 0.01=\alpha[/latex], we do not reject the null hypothesis.  At the 1% significance level there is not enough evidence to suggest that the proportion of visitors who make a purchase is lower than 93%.

• The null hypothesis [latex]p=93\%[/latex] is the claim that 93% of visitors to the website make a purchase.
• The alternative hypothesis [latex]p \lt 93\%[/latex] is the claim that less than 93% of visitors to the website make a purchase.
• The function is binom.dist because we are finding the probability of at most 45 successes.
• Field 1 is the number of successes [latex]x[/latex].
• Field 2 is the sample size [latex]n[/latex].
• Field 3 is the probability of success [latex]p[/latex].  This is the claim about the population proportion made in the null hypothesis, so that means we assume [latex]p=0.93[/latex].
• The p -value of 0.2710 tells us that under the assumption that 93% of visitors make a purchase (the null hypothesis), there is a 27.10% chance that the number of visitors in a sample of 50 who make a purchase is 45 or less.  This is a large probability compared to the significance level, and so is likely to happen assuming the null hypothesis is true.  This suggests that the assumption that the null hypothesis is true is most likely correct, and so the conclusion of the test is to not reject the null hypothesis.  In other words, the proportion of visitors to the website who make a purchase adults is most likely 93%.

A drug company claims that only 4% of people who take their new drug experience any side effects from the drug.  A researcher believes that the percent is higher than drug company’s claim.  The researcher takes a sample of 80 people who take the drug and finds that 10% of the people in the sample experience side effects from the drug.  At the 5% significance level, determine if the proportion of people who experience side effects from taking the drug is higher than claimed.

[latex]\begin{eqnarray*} H_0: & & p=4\% \mbox{ of people experience side effects} \\ H_a: & & p \gt 4\% \mbox{ of people experience side effects} \end{eqnarray*}[/latex]

From the question, we have [latex]n=80[/latex], [latex]\hat{p}=0.1[/latex], and [latex]\alpha=0.05[/latex].

To determine the distribution, we check [latex]n \times p[/latex] and [latex]n \times (1-p)[/latex].  For the value of [latex]p[/latex], we use the claim from the null hypothesis ([latex]p=0.04[/latex]).

[latex]\begin{eqnarray*} n \times p & = & 80 \times 0.04=3.2 \lt 5\end{eqnarray*}[/latex]

Because [latex]n \times p  \lt 5[/latex] we use a binomial distribution to calculate the p -value.  Because the alternative hypothesis is a [latex]\gt[/latex], the p -value is the probability of getting at least 8 successes in 80 trials.  (Note:  In the sample of size 80, 10% have the characteristic of interest, so this means that [latex]80 \times 0.1=8[/latex] people in the sample have the characteristic of interest.)

So the p -value[latex]=0.0147[/latex].

Because p -value[latex]=0.0147 \lt 0.05=\alpha[/latex], we reject the null hypothesis in favour of the alternative hypothesis.  At the 5% significance level there is enough evidence to suggest that the proportion of people who experience side effects from taking the drug is higher than 4%.

• The null hypothesis [latex]p=4\%[/latex] is the claim that 4% of the people experience side effects from taking the drug.
• The alternative hypothesis [latex]p \gt 4\%[/latex] is the claim that more than 4% of the people experience side effects from taking the drug.
• The function is 1-binom.dist because we are finding the probability of at least 8 successes.
• Field 1 is [latex]x-1[/latex] where [latex]x[/latex] is the number of successes.  In this case, we are using the compliment rule to change the probability of at least 8 successes into 1 minus the probability of at most 7 successes.
• Field 3 is the probability of success [latex]p[/latex].  This is the claim about the population proportion made in the null hypothesis, so that means we assume [latex]p=0.04[/latex].
• The p -value of 0.0147 tells us that under the assumption that 4% of people experience side effects (the null hypothesis), there is a 1.47% chance that the number of people in a sample of 80 who experience side effects is 8 or more.  This is a small probability compared to the significance level, and so is unlikely to happen assuming the null hypothesis is true.  This suggests that the assumption that the null hypothesis is true is most likely incorrect, and so the conclusion of the test is to reject the null hypothesis in favour of the alternative hypothesis.  In other words, the proportion of people who experience side effects is most likely greater than 4%.

Concept Review

The hypothesis test for a population proportion is a well-established process:

• Find the p -value (the area in the corresponding tail) for the test using the appropriate distribution (normal or binomial).
• Compare the p -value to the significance level and state the outcome of the test.

Attribution

“ 9.6   Hypothesis Testing of a Single Mean and Single Proportion “ in Introductory Statistics by OpenStax  is licensed under a  Creative Commons Attribution 4.0 International License.

Introduction to Statistics Copyright © 2022 by Valerie Watts is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License , except where otherwise noted.

Teach yourself statistics

Hypothesis Test for a Mean

This lesson explains how to conduct a hypothesis test of a mean, when the following conditions are met:

• The sampling method is simple random sampling .
• The sampling distribution is normal or nearly normal.

Generally, the sampling distribution will be approximately normally distributed if any of the following conditions apply.

• The population distribution is normal.
• The population distribution is symmetric , unimodal , without outliers , and the sample size is 15 or less.
• The population distribution is moderately skewed , unimodal, without outliers, and the sample size is between 16 and 40.
• The sample size is greater than 40, without outliers.

This approach consists of four steps: (1) state the hypotheses, (2) formulate an analysis plan, (3) analyze sample data, and (4) interpret results.

State the Hypotheses

Every hypothesis test requires the analyst to state a null hypothesis and an alternative hypothesis . The hypotheses are stated in such a way that they are mutually exclusive. That is, if one is true, the other must be false; and vice versa.

The table below shows three sets of hypotheses. Each makes a statement about how the population mean μ is related to a specified value M . (In the table, the symbol ≠ means " not equal to ".)

The first set of hypotheses (Set 1) is an example of a two-tailed test , since an extreme value on either side of the sampling distribution would cause a researcher to reject the null hypothesis. The other two sets of hypotheses (Sets 2 and 3) are one-tailed tests , since an extreme value on only one side of the sampling distribution would cause a researcher to reject the null hypothesis.

Formulate an Analysis Plan

The analysis plan describes how to use sample data to accept or reject the null hypothesis. It should specify the following elements.

• Significance level. Often, researchers choose significance levels equal to 0.01, 0.05, or 0.10; but any value between 0 and 1 can be used.
• Test method. Use the one-sample t-test to determine whether the hypothesized mean differs significantly from the observed sample mean.

Analyze Sample Data

Using sample data, conduct a one-sample t-test. This involves finding the standard error, degrees of freedom, test statistic, and the P-value associated with the test statistic.

SE = s * sqrt{ ( 1/n ) * [ ( N - n ) / ( N - 1 ) ] }

SE = s / sqrt( n )

• Degrees of freedom. The degrees of freedom (DF) is equal to the sample size (n) minus one. Thus, DF = n - 1.

t = ( x - μ) / SE

• P-value. The P-value is the probability of observing a sample statistic as extreme as the test statistic. Since the test statistic is a t statistic, use the t Distribution Calculator to assess the probability associated with the t statistic, given the degrees of freedom computed above. (See sample problems at the end of this lesson for examples of how this is done.)

Sample Size Calculator

As you probably noticed, the process of hypothesis testing can be complex. When you need to test a hypothesis about a mean score, consider using the Sample Size Calculator. The calculator is fairly easy to use, and it is free. You can find the Sample Size Calculator in Stat Trek's main menu under the Stat Tools tab. Or you can tap the button below.

Interpret Results

If the sample findings are unlikely, given the null hypothesis, the researcher rejects the null hypothesis. Typically, this involves comparing the P-value to the significance level , and rejecting the null hypothesis when the P-value is less than the significance level.

Test Your Understanding

In this section, two sample problems illustrate how to conduct a hypothesis test of a mean score. The first problem involves a two-tailed test; the second problem, a one-tailed test.

Problem 1: Two-Tailed Test

An inventor has developed a new, energy-efficient lawn mower engine. He claims that the engine will run continuously for 5 hours (300 minutes) on a single gallon of regular gasoline. From his stock of 2000 engines, the inventor selects a simple random sample of 50 engines for testing. The engines run for an average of 295 minutes, with a standard deviation of 20 minutes. Test the null hypothesis that the mean run time is 300 minutes against the alternative hypothesis that the mean run time is not 300 minutes. Use a 0.05 level of significance. (Assume that run times for the population of engines are normally distributed.)

Solution: The solution to this problem takes four steps: (1) state the hypotheses, (2) formulate an analysis plan, (3) analyze sample data, and (4) interpret results. We work through those steps below:

Null hypothesis: μ = 300

Alternative hypothesis: μ ≠ 300

• Formulate an analysis plan . For this analysis, the significance level is 0.05. The test method is a one-sample t-test .

SE = s / sqrt(n) = 20 / sqrt(50) = 20/7.07 = 2.83

DF = n - 1 = 50 - 1 = 49

t = ( x - μ) / SE = (295 - 300)/2.83 = -1.77

where s is the standard deviation of the sample, x is the sample mean, μ is the hypothesized population mean, and n is the sample size.

Since we have a two-tailed test , the P-value is the probability that the t statistic having 49 degrees of freedom is less than -1.77 or greater than 1.77. We use the t Distribution Calculator to find P(t < -1.77) is about 0.04.

• If you enter 1.77 as the sample mean in the t Distribution Calculator, you will find the that the P(t < 1.77) is about 0.04. Therefore, P(t >  1.77) is 1 minus 0.96 or 0.04. Thus, the P-value = 0.04 + 0.04 = 0.08.
• Interpret results . Since the P-value (0.08) is greater than the significance level (0.05), we cannot reject the null hypothesis.

Note: If you use this approach on an exam, you may also want to mention why this approach is appropriate. Specifically, the approach is appropriate because the sampling method was simple random sampling, the population was normally distributed, and the sample size was small relative to the population size (less than 5%).

Problem 2: One-Tailed Test

Bon Air Elementary School has 1000 students. The principal of the school thinks that the average IQ of students at Bon Air is at least 110. To prove her point, she administers an IQ test to 20 randomly selected students. Among the sampled students, the average IQ is 108 with a standard deviation of 10. Based on these results, should the principal accept or reject her original hypothesis? Assume a significance level of 0.01. (Assume that test scores in the population of engines are normally distributed.)

Null hypothesis: μ >= 110

Alternative hypothesis: μ < 110

• Formulate an analysis plan . For this analysis, the significance level is 0.01. The test method is a one-sample t-test .

SE = s / sqrt(n) = 10 / sqrt(20) = 10/4.472 = 2.236

DF = n - 1 = 20 - 1 = 19

t = ( x - μ) / SE = (108 - 110)/2.236 = -0.894

Here is the logic of the analysis: Given the alternative hypothesis (μ < 110), we want to know whether the observed sample mean is small enough to cause us to reject the null hypothesis.

The observed sample mean produced a t statistic test statistic of -0.894. We use the t Distribution Calculator to find P(t < -0.894) is about 0.19.

• This means we would expect to find a sample mean of 108 or smaller in 19 percent of our samples, if the true population IQ were 110. Thus the P-value in this analysis is 0.19.
• Interpret results . Since the P-value (0.19) is greater than the significance level (0.01), we cannot reject the null hypothesis.

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons
• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

10.29: Hypothesis Test for a Difference in Two Population Means (1 of 2)

• Last updated
• Save as PDF
• Page ID 14167

Learning Objectives

• Under appropriate conditions, conduct a hypothesis test about a difference between two population means. State a conclusion in context.

Using the Hypothesis Test for a Difference in Two Population Means

The general steps of this hypothesis test are the same as always. As expected, the details of the conditions for use of the test and the test statistic are unique to this test (but similar in many ways to what we have seen before.)

Step 1: Determine the hypotheses.

The hypotheses for a difference in two population means are similar to those for a difference in two population proportions. The null hypothesis, H 0 , is again a statement of “no effect” or “no difference.”

• H 0 : μ 1 – μ 2 = 0, which is the same as H 0 : μ 1 = μ 2

The alternative hypothesis, H a , can be any one of the following.

• H a : μ 1 – μ 2 < 0, which is the same as H a : μ 1 < μ 2
• H a : μ 1 – μ 2 > 0, which is the same as H a : μ 1 > μ 2
• H a : μ 1 – μ 2 ≠ 0, which is the same as H a : μ 1 ≠ μ 2

Step 2: Collect the data.

As usual, how we collect the data determines whether we can use it in the inference procedure. We have our usual two requirements for data collection.

• Samples must be random to remove or minimize bias.
• Samples must be representative of the populations in question.

We use this hypothesis test when the data meets the following conditions.

• The two random samples are independent .
• The variable is normally distributed in both populations . If this variable is not known, samples of more than 30 will have a difference in sample means that can be modeled adequately by the t-distribution. As we discussed in “Hypothesis Test for a Population Mean,” t-procedures are robust even when the variable is not normally distributed in the population. If checking normality in the populations is impossible, then we look at the distribution in the samples. If a histogram or dotplot of the data does not show extreme skew or outliers, we take it as a sign that the variable is not heavily skewed in the populations, and we use the inference procedure. (Note: This is the same condition we used for the one-sample t-test in “Hypothesis Test for a Population Mean.”)

Step 3: Assess the evidence.

If the conditions are met, then we calculate the t-test statistic. The t-test statistic has a familiar form.

Since the null hypothesis assumes there is no difference in the population means, the expression (μ 1 – μ 2 ) is always zero.

As we learned in “Estimating a Population Mean,” the t-distribution depends on the degrees of freedom (df) . In the one-sample and matched-pair cases df = n – 1. For the two-sample t-test, determining the correct df is based on a complicated formula that we do not cover in this course. We will either give the df or use technology to find the df . With the t-test statistic and the degrees of freedom, we can use the appropriate t-model to find the P-value, just as we did in “Hypothesis Test for a Population Mean.” We can even use the same simulation.

Step 4: State a conclusion.

To state a conclusion, we follow what we have done with other hypothesis tests. We compare our P-value to a stated level of significance.

• If the P-value ≤ α, we reject the null hypothesis in favor of the alternative hypothesis.
• If the P-value > α, we fail to reject the null hypothesis. We do not have enough evidence to support the alternative hypothesis.

As always, we state our conclusion in context, usually by referring to the alternative hypothesis.

“Context and Calories”

Does the company you keep impact what you eat? This example comes from an article titled “Impact of Group Settings and Gender on Meals Purchased by College Students” (Allen-O’Donnell, M., T. C. Nowak, K. A. Snyder, and M. D. Cottingham, Journal of Applied Social Psychology 49(9), 2011, onlinelibrary.wiley.com/doi/10.1111/j.1559-1816.2011.00804.x/full) . In this study, researchers examined this issue in the context of gender-related theories in their field. For our purposes, we look at this research more narrowly.

Step 1: Stating the hypotheses.

In the article, the authors make the following hypothesis. “The attempt to appear feminine will be empirically demonstrated by the purchase of fewer calories by women in mixed-gender groups than by women in same-gender groups.” We translate this into a simpler and narrower research question: Do women purchase fewer calories when they eat with men compared to when they eat with women?

Here the two populations are “women eating with women” (population 1) and “women eating with men” (population 2). The variable is the calories in the meal. We test the following hypotheses at the 5% level of significance.

The null hypothesis is always H 0 : μ 1 – μ 2 = 0, which is the same as H 0 : μ 1 = μ 2 .

The alternative hypothesis H a : μ 1 – μ 2 > 0, which is the same as H a : μ 1 > μ 2 .

Here μ 1 represents the mean number of calories ordered by women when they were eating with other women, and μ 2 represents the mean number of calories ordered by women when they were eating with men.

Note: It does not matter which population we label as 1 or 2, but once we decide, we have to stay consistent throughout the hypothesis test. Since we expect the number of calories to be greater for the women eating with other women, the difference is positive if “women eating with women” is population 1. If you prefer to work with positive numbers, choose the group with the larger expected mean as population 1. This is a good general tip.

Step 2: Collect Data.

As usual, there are two major things to keep in mind when considering the collection of data.

• Samples need to be representative of the population in question.
• Samples need to be random in order to remove or minimize bias.

Representative Samples?

The researchers state their hypothesis in terms of “women.” We did the same. But the researchers gathered data by watching people eat at the HUB Rock Café II on the campus of Indiana University of Pennsylvania during the Spring semester of 2006. Almost all of the women in the data set were white undergraduates between the ages of 18 and 24, so there are some definite limitations on the scope of this study. These limitations will affect our conclusion (and the specific definition of the population means in our hypotheses.)

Random Samples?

The observations were collected on February 13, 2006, through February 22, 2006, between 11 a.m. and 7 p.m. We can see that the researchers included both lunch and dinner. They also made observations on all days of the week to ensure that weekly customer patterns did not confound their findings. The authors state that “since the time period for observations and the place where [they] observed students were limited, the sample was a convenience sample.” Despite these limitations, the researchers conducted inference procedures with the data, and the results were published in a reputable journal. We will also conduct inference with this data, but we also include a discussion of the limitations of the study with our conclusion. The authors did this, also.

Do the data met the conditions for use of a t-test?

The researchers reported the following sample statistics.

• In a sample of 45 women dining with other women, the average number of calories ordered was 850, and the standard deviation was 252.
• In a sample of 27 women dining with men, the average number of calories ordered was 719, and the standard deviation was 322.

One of the samples has fewer than 30 women. We need to make sure the distribution of calories in this sample is not heavily skewed and has no outliers, but we do not have access to a spreadsheet of the actual data. Since the researchers conducted a t-test with this data, we will assume that the conditions are met. This includes the assumption that the samples are independent.

As noted previously, the researchers reported the following sample statistics.

To compute the t-test statistic, make sure sample 1 corresponds to population 1. Here our population 1 is “women eating with other women.” So x 1 = 850, s 1 = 252, n 1 =45, and so on.

Using technology, we determined that the degrees of freedom are about 45 for this data. To find the P-value, we use our familiar simulation of the t-distribution. Since the alternative hypothesis is a “greater than” statement, we look for the area to the right of T = 1.81. The P-value is 0.0385.

Generic Conclusion

The hypotheses for this test are H 0 : μ 1 – μ 2 = 0 and H a : μ 1 – μ 2 > 0. Since the P-value is less than the significance level (0.0385 < 0.05), we reject H 0 and accept H a .

Conclusion in context

At Indiana University of Pennsylvania, the mean number of calories ordered by undergraduate women eating with other women is greater than the mean number of calories ordered by undergraduate women eating with men (P-value = 0.0385).

Comment about Conclusions

In the conclusion above, we did not generalize the findings to all women. Since the samples included only undergraduate women at one university, we included this information in our conclusion. But our conclusion is a cautious statement of the findings. The authors see the results more broadly in the context of theories in the field of social psychology. In the context of these theories, they write, “Our findings support the assertion that meal size is a tool for influencing the impressions of others. For traditional-age, predominantly White college women, diminished meal size appears to be an attempt to assert femininity in groups that include men.” This viewpoint is echoed in the following summary of the study for the general public on National Public Radio (npr.org).

• Both men and women appear to choose larger portions when they eat with women, and both men and women choose smaller portions when they eat in the company of men, according to new research published in the Journal of Applied Social Psychology . The study, conducted among a sample of 127 college students, suggests that both men and women are influenced by unconscious scripts about how to behave in each other’s company. And these scripts change the way men and women eat when they eat together and when they eat apart.

Should we be concerned that the findings of this study are generalized in this way? Perhaps. But the authors of the article address this concern by including the following disclaimer with their findings: “While the results of our research are suggestive, they should be replicated with larger, representative samples. Studies should be done not only with primarily White, middle-class college students, but also with students who differ in terms of race/ethnicity, social class, age, sexual orientation, and so forth.” This is an example of good statistical practice. It is often very difficult to select truly random samples from the populations of interest. Researchers therefore discuss the limitations of their sampling design when they discuss their conclusions.

In the following activities, you will have the opportunity to practice parts of the hypothesis test for a difference in two population means. On the next page, the activities focus on the entire process and also incorporate technology.

National Health and Nutrition Survey

https://assessments.lumenlearning.co...sessments/3705

https://assessments.lumenlearning.co...sessments/3782

https://assessments.lumenlearning.co...sessments/3706

Contributors and Attributions

• Concepts in Statistics. Provided by : Open Learning Initiative. Located at : http://oli.cmu.edu . License : CC BY: Attribution

9.6 Hypothesis Testing of a Single Mean and Single Proportion

Hypothesis testing of a single mean and single proportion.

Class Time:

• The student will select the appropriate distributions to use in each case.
• The student will conduct hypothesis tests and interpret the results.

Television Survey In a recent survey, it was stated that Americans watch television on average four hours per day. Assume that σ = 2. Using your class as the sample, conduct a hypothesis test to determine if the average for students at your school is lower.

• H 0 : _____________
• H a : _____________
• In words, define the random variable. __________ = ______________________
• The distribution to use for the test is _______________________.
• Determine the test statistic using your data.
• Determine the p -value.
• Do you or do you not reject the null hypothesis? Why?
• Write a clear conclusion using a complete sentence.

Language Survey About 42.3% of Californians and 19.6% of all Americans over age five speak a language other than English at home. Using your class as the sample, conduct a hypothesis test to determine if the percent of the students at your school who speak a language other than English at home is different from 42.3%.

• H 0 : ___________
• H a : ___________
• In words, define the random variable. __________ = _______________
• The distribution to use for the test is ________________

Jeans Survey Suppose that young adults own an average of three pairs of jeans. Survey eight people from your class to determine if the average is higher than three. Assume the population is normal.

As an Amazon Associate we earn from qualifying purchases.

This book may not be used in the training of large language models or otherwise be ingested into large language models or generative AI offerings without OpenStax's permission.

Want to cite, share, or modify this book? This book uses the Creative Commons Attribution License and you must attribute OpenStax.

Access for free at https://openstax.org/books/introductory-statistics/pages/1-introduction

• Authors: Barbara Illowsky, Susan Dean
• Publisher/website: OpenStax
• Book title: Introductory Statistics
• Publication date: Sep 19, 2013
• Location: Houston, Texas
• Book URL: https://openstax.org/books/introductory-statistics/pages/1-introduction
• Section URL: https://openstax.org/books/introductory-statistics/pages/9-6-hypothesis-testing-of-a-single-mean-and-single-proportion

© Jun 23, 2022 OpenStax. Textbook content produced by OpenStax is licensed under a Creative Commons Attribution License . The OpenStax name, OpenStax logo, OpenStax book covers, OpenStax CNX name, and OpenStax CNX logo are not subject to the Creative Commons license and may not be reproduced without the prior and express written consent of Rice University.

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons
• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

8.7: Hypothesis Test of Single Population Proportion with Examples

• Last updated
• Save as PDF
• Page ID 130292

Steps for performing Hypothesis Test for a Single Population Proportion

Step 1: State your hypotheses about the population proportion. Step 2: Summarize the data. State a significance level. State and check conditions required for the procedure

• \(\hat{P}=\frac{X}{n}\)
• Sample is random with independent observations .
• Sample is large. Check that the sample has 5 or more expected successes and 5 or more expected failures
• Population is large relative to the sample size . The population size is at least 10 times bigger than the sample size.

Step 3: Perform the procedure

• Find the Standard Error (SE) based on the assumption that \(H_{0}\) is true.
• Compute the observed value of the test statistic \(Z_{obs}\).
• Find the p-value in order to measure your level of surprise.

Step 4: Make a decision about \(H_{0}\) and \(H_{a}\)

• Do you reject or not reject your null hypothesis? What about the alternative hypothesis?

Step 5 : Make a conclusion.

• What does this mean in the context of the data?

Examples: Hypothesis Test for a Single Population Proportion

Example \(\pageindex{1}\).

Joon believes that 50% of first-time brides in the United States are younger than their grooms. She performs a hypothesis test to determine if the percentage is the same or different from 50% . Joon samples 100 first-time brides and 53 reply that they are younger than their grooms. For the hypothesis test, she uses a 1% level of significance.

Set up the hypothesis test:

The 1% level of significance means that α = 0.01. This is a test of a single population proportion .

\(H_{0}: p = 0.50\)  \(H_{a}: p \neq 0.50\)

The words "is the same or different from" tell you this is a two-tailed test.

Calculate the distribution needed:

Random variable: \(\hat{P} =\) the percent of of first-time brides who are younger than their grooms.

Distribution for the test: The problem contains no mention of a mean. The information is given in terms of percentages. Use the Normal distribution for \hat{P} , the estimated proportion.

\[ \hat{P} - N\left(p, \sqrt{\frac{p(1-p)}{n}}\right)\nonumber \]

\[ \hat{P} - N\left(0.5, \sqrt{\frac{0.5(0.5)}{100}}\right)\nonumber \]

where \(p = 0.50, q = 1−p = 0.50\), and \(n = 100\)

Calculate the p -value using the normal distribution for proportions:

\[p\text{-value} = P( \hat{P} < 0.47 \space or \space \hat{P} > 0.53) = 0.5485\nonumber \]

where \[x = 53, \hat{P} = \frac{x}{n} = \frac{53}{100} = 0.53\nonumber \].

Interpretation of the p-value: If the null hypothesis is true, there is 0.5485 probability (54.85%) that the sample (estimated) proportion \( \hat{P} \) is 0.53 or more OR 0.47 or less (see the graph in Figure).

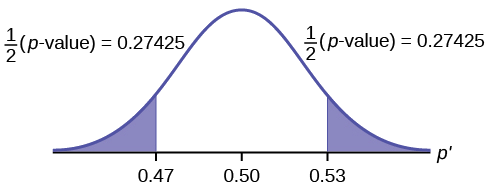
\(\mu = p = 0.50\) comes from \(H_{0}\), the null hypothesis.

\( \hat{P} = 0.53\). Since the curve is symmetrical and the test is two-tailed, the \( \hat{P} \) for the left tail is equal to \(0.50 – 0.03 = 0.47\) where \(\mu = p = 0.50\). (0.03 is the difference between 0.53 and 0.50.)

Compare \(\alpha\) and the \(p\text{-value}\):

Since \(\alpha = 0.01\) and \(p\text{-value} = 0.5485\). \(\alpha < p\text{-value}\).

Make a decision: Since \(\alpha < p\text{-value}\), you cannot reject \(H_{0}\).

Conclusion: At the 1% level of significance, the sample data do not show sufficient evidence that the percentage of first-time brides who are younger than their grooms is different from 50%.

The \(p\text{-value}\) can easily be calculated.

Press STAT and arrow over to TESTS . Press 5:1-PropZTest . Enter .5 for \(p_{0}\), 53 for \(x\) and 100 for \(n\). Arrow down to Prop and arrow to not equals \(p_{0}\). Press ENTER . Arrow down to Calculate and press ENTER . The calculator calculates the \(p\text{-value}\) (\(p = 0.5485\)) and the test statistic (\(z\)-score). Prop not equals .5 is the alternate hypothesis. Do this set of instructions again except arrow to Draw (instead of Calculate ). Press ENTER . A shaded graph appears with \(z = 0.6\) (test statistic) and \(p = 0.5485\) (\(p\text{-value}\)). Make sure when you use Draw that no other equations are highlighted in \(Y =\) and the plots are turned off.

The Type I and Type II errors are as follows:

The Type I error is to conclude that the proportion of first-time brides who are younger than their grooms is different from 50% when, in fact, the proportion is actually 50%. (Reject the null hypothesis when the null hypothesis is true).

The Type II error is there is not enough evidence to conclude that the proportion of first time brides who are younger than their grooms differs from 50% when, in fact, the proportion does differ from 50%. (Do not reject the null hypothesis when the null hypothesis is false.)

Exercise \(\PageIndex{1}\)

A teacher believes that 85% of students in the class will want to go on a field trip to the local zoo. She performs a hypothesis test to determine if the percentage is the same or different from 85%. The teacher samples 50 students and 39 reply that they would want to go to the zoo. For the hypothesis test, use a 1% level of significance.

First, determine what type of test this is, set up the hypothesis test, find the \(p\text{-value}\), sketch the graph, and state your conclusion.

Since the problem is about percentages, this is a test of single population proportions.

• \(H_{0} : p = 0.85\)
• \(H_{a}: p \neq 0.85\)
• \(p-value = 0.7554\)

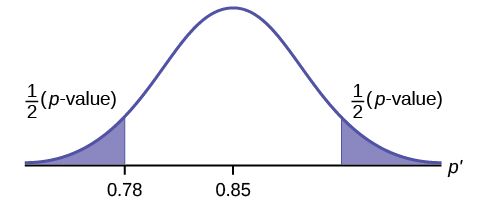
Because \(p > \alpha\), we fail to reject the null hypothesis. There is not sufficient evidence to suggest that the proportion of students that want to go to the zoo is not 85%.

Example \(\PageIndex{2}\)

Suppose a consumer group suspects that the proportion of households that have three cell phones is 30%. A cell phone company has reason to believe that the proportion is not 30%. Before they start a big advertising campaign, they conduct a hypothesis test. Their marketing people survey 150 households with the result that 43 of the households have three cell phones.

Set up the Hypothesis Test:

\(H_{0}: p = 0.30, H_{a}: p \neq 0.30\)

Determine the distribution needed:

The random variable is \( \hat{P} =\) proportion of households that have three cell phones.

The distribution for the hypothesis test is \( \hat{P} - N\left(0.30, \sqrt{\frac{0.30 \cdot (0.70)}{150}}\right)\)

Exercise \(\PageIndex{2}\).2

a. The value that helps determine the \(p\text{-value}\) is \( \hat{P} \). Calculate \( \hat{P} \).

a. \( \hat{P} = \frac{x}{n}\) where \(x\) is the number of successes and \(n\) is the total number in the sample.

\(x = 43, n = 150\)

\( \hat{P} = 43/150=0.2867\)

Exercise \(\PageIndex{2}\).3

b. What is a success for this problem?

b. A success is having three cell phones in a household.

Exercise \(\PageIndex{2}\).4

c. What is the level of significance?

c. The level of significance is the preset \(\alpha\). Since \(\alpha\) is not given, assume that \(\alpha = 0.05\).

Exercise \(\PageIndex{2}\).5

d. Draw the graph for this problem. Draw the horizontal axis. Label and shade appropriately.

Calculate the \(p\text{-value}\).

d. \(p\text{-value} = 0.7216\)

Exercise \(\PageIndex{2}\).6

e. Make a decision. _____________(Reject/Do not reject) \(H_{0}\) because____________.

e. Assuming that \(\alpha = 0.05, \alpha < p\text{-value}\). The decision is do not reject \(H_{0}\) because there is not sufficient evidence to conclude that the proportion of households that have three cell phones is not 30%.

Exercise \(\PageIndex{2}\)

Marketers believe that 92% of adults in the United States own a cell phone. A cell phone manufacturer believes that number is actually lower. 200 American adults are surveyed, of which, 174 report having cell phones. Use a 5% level of significance. State the null and alternative hypothesis, find the p -value, state your conclusion, and identify the Type I and Type II errors.

• \(H_{0}: p = 0.92\)
• \(H_{a}: p < 0.92\)
• \(p\text{-value} = 0.0046\)

Because \(p < 0.05\), we reject the null hypothesis. There is sufficient evidence to conclude that fewer than 92% of American adults own cell phones.

• Type I Error: To conclude that fewer than 92% of American adults own cell phones when, in fact, 92% of American adults do own cell phones (reject the null hypothesis when the null hypothesis is true).
• Type II Error: To conclude that 92% of American adults own cell phones when, in fact, fewer than 92% of American adults own cell phones (do not reject the null hypothesis when the null hypothesis is false).

The next example is a poem written by a statistics student named Nicole Hart. The solution to the problem follows the poem. Notice that the hypothesis test is for a single population proportion. This means that the null and alternate hypotheses use the parameter \(p\). The distribution for the test is normal. The estimated proportion \(\hat{p}\) is the proportion of fleas killed to the total fleas found on Fido. This is sample information. The problem gives a preconceived \(\alpha = 0.01\), for comparison, and a 95% confidence interval computation. The poem is clever and humorous, so please enjoy it!

Example \(\PageIndex{3}\)

My dog has so many fleas,

They do not come off with ease. As for shampoo, I have tried many types Even one called Bubble Hype, Which only killed 25% of the fleas, Unfortunately I was not pleased.

I've used all kinds of soap, Until I had given up hope Until one day I saw An ad that put me in awe.

A shampoo used for dogs Called GOOD ENOUGH to Clean a Hog Guaranteed to kill more fleas.

I gave Fido a bath And after doing the math His number of fleas Started dropping by 3's! Before his shampoo I counted 42.

At the end of his bath, I redid the math And the new shampoo had killed 17 fleas. So now I was pleased.

Now it is time for you to have some fun With the level of significance being .01, You must help me figure out

Use the new shampoo or go without?

\(H_{0}: p \leq 0.25\)   \(H_{a}: p > 0.25\)

In words, CLEARLY state what your random variable \(\bar{X}\) or \( \hat{P} \) represents.

\( \hat{P} =\) The proportion of fleas that are killed by the new shampoo

State the distribution to use for the test.

\[N\left(0.25, \sqrt{\frac{0.25 \cdot (1-0.25)}{42}}\right)\nonumber \]

Test Statistic: \(z_{obs} = 2.3163\)

Calculate the \(p\text{-value}\) using the normal distribution for proportions:

\[p\text{-value} = 0.0103\nonumber \]

In one to two complete sentences, explain what the p -value means for this problem.

If the null hypothesis is true (the proportion is 0.25), then there is a 0.0103 probability that the sample (estimated) proportion is 0.4048 \(\left(\frac{17}{42}\right)\) or more.

Use the previous information to sketch a picture of this situation. CLEARLY, label and scale the horizontal axis and shade the region(s) corresponding to the \(p\text{-value}\).

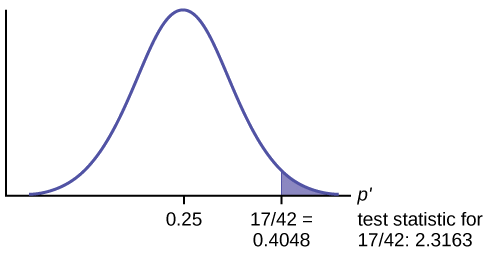
Indicate the correct decision (“reject” or “do not reject” the null hypothesis), the reason for it, and write an appropriate conclusion, using complete sentences.

Conclusion: At the 1% level of significance, the sample data do not show sufficient evidence that the percentage of fleas that are killed by the new shampoo is more than 25%.

Construct a 95% confidence interval for the true mean or proportion. Include a sketch of the graph of the situation. Label the point estimate and the lower and upper bounds of the confidence interval.

Confidence Interval: (0.26,0.55) We are 95% confident that the true population proportion p of fleas that are killed by the new shampoo is between 26% and 55%.

This test result is not very definitive since the \(p\text{-value}\) is very close to alpha. In reality, one would probably do more tests by giving the dog another bath after the fleas have had a chance to return.

Example \(\PageIndex{4}\)

In a study of 420,019 cell phone users, 172 of the subjects developed brain cancer. Test the claim that cell phone users developed brain cancer at a greater rate than that for non-cell phone users (the rate of brain cancer for non-cell phone users is 0.0340%). Since this is a critical issue, use a 0.005 significance level. Explain why the significance level should be so low in terms of a Type I error.

We will follow the four-step process.

If we commit a Type I error, we are essentially accepting a false claim. Since the claim describes cancer-causing environments, we want to minimize the chances of incorrectly identifying causes of cancer.

• \(H_{0}: p \leq 0.00034\)
• \(H_{a}: p > 0.00034\)
• \(\hat{P}=\frac{172}{420,019}=0.00041\).
• The sample is sufficiently large because we have \(np = 420,019(0.00034) = 142.8\), \(nq = 420,019(0.99966) = 419,876.2\) both greater than five. Sample is random with independent observations. Thus we will be able to generalize our results to the population.
• \(SE=\sqrt{\frac{0.00034(1-0.00034)}{420,019}}=0.000028\)
• \(Z_{obs}=\frac{0.00041-0.00034}{0.000028}=2.5\)
• \(p\text{-value} = 1-P(Z<2.5)=0.0062\)
• Since the \(p\text{-value} = 0.0062\) is greater than our alpha value \(= 0.005\), we cannot reject the null and cannot support alternative.
• Therefore, we conclude that there is not enough evidence to support the claim of higher brain cancer rates for the cell phone users.

Example \(\PageIndex{5}\)

According to the US Census there are approximately 268,608,618 residents aged 12 and older. Statistics from the Rape, Abuse, and Incest National Network indicate that, on average, 207,754 rapes occur each year (male and female) for persons aged 12 and older. This translates into a percentage of sexual assaults of 0.078%. In Daviess County, KY, there were reported 11 rapes for a population of 37,937. Conduct an appropriate hypothesis test to determine if there is a statistically significant difference between the local sexual assault percentage and the national sexual assault percentage. Use a significance level of 0.01.

We will follow the five-step plan.

• We need to test whether the proportion of sexual assaults in Daviess County, KY is significantly different from the national average.
• \(H_{0}: p = 0.00078\)
• \(H_{a}: p \neq 0.00078\)
• \(p\text{-value} = 0.00063\)
• Since the \(p\text{-value} = 0.00063\), is less than the alpha level of 0.01, the sample data indicates that we should reject the null hypothesis.
• In conclusion, the sample data support the claim that the proportion of sexual assaults in Daviess County, Kentucky is different from the national average proportion.

The hypothesis test itself has an established process. This can be summarized as follows:

• Determine \(H_{0}\) and \(H_{a}\). Remember, they are contradictory.
• Determine the random variable.
• Determine the distribution for the test.
• Draw a graph, calculate the test statistic, and use the test statistic to calculate the \(p\text{-value}\). (A z -score (\(Z_{obs}\) is an example of test statistics.)
• Compare the preconceived α with the p -value, make a decision (reject or do not reject H 0 ), and write a clear conclusion using English sentences.

Notice that in performing the hypothesis test, you use \(\alpha\) and not \(\beta\). \(\beta\) is needed to help determine the sample size of the data that is used in calculating the \(p\text{-value}\). Remember that the quantity \(1 – \beta\) is called the Power of the Test . A high power is desirable. If the power is too low, statisticians typically increase the sample size while keeping α the same.If the power is low, the null hypothesis might not be rejected when it should be.

• Data from Amit Schitai. Director of Instructional Technology and Distance Learning. LBCC.
• Data from Bloomberg Businessweek . Available online at www.businessweek.com/news/2011- 09-15/nyc-smoking-rate-falls-to-record-low-of-14-bloomberg-says.html.
• Data from energy.gov. Available online at http://energy.gov (accessed June 27. 2013).
• Data from Gallup®. Available online at www.gallup.com (accessed June 27, 2013).
• Data from Growing by Degrees by Allen and Seaman.
• Data from La Leche League International. Available online at www.lalecheleague.org/Law/BAFeb01.html.
• Data from the American Automobile Association. Available online at www.aaa.com (accessed June 27, 2013).
• Data from the American Library Association. Available online at www.ala.org (accessed June 27, 2013).
• Data from the Bureau of Labor Statistics. Available online at http://www.bls.gov/oes/current/oes291111.htm .
• Data from the Centers for Disease Control and Prevention. Available online at www.cdc.gov (accessed June 27, 2013)
• Data from the U.S. Census Bureau, available online at quickfacts.census.gov/qfd/states/00000.html (accessed June 27, 2013).
• Data from the United States Census Bureau. Available online at www.census.gov/hhes/socdemo/language/.
• Data from Toastmasters International. Available online at http://toastmasters.org/artisan/deta...eID=429&Page=1 .
• Data from Weather Underground. Available online at www.wunderground.com (accessed June 27, 2013).
• Federal Bureau of Investigations. “Uniform Crime Reports and Index of Crime in Daviess in the State of Kentucky enforced by Daviess County from 1985 to 2005.” Available online at http://www.disastercenter.com/kentucky/crime/3868.htm (accessed June 27, 2013).
• “Foothill-De Anza Community College District.” De Anza College, Winter 2006. Available online at research.fhda.edu/factbook/DA...t_da_2006w.pdf.
• Johansen, C., J. Boice, Jr., J. McLaughlin, J. Olsen. “Cellular Telephones and Cancer—a Nationwide Cohort Study in Denmark.” Institute of Cancer Epidemiology and the Danish Cancer Society, 93(3):203-7. Available online at http://www.ncbi.nlm.nih.gov/pubmed/11158188 (accessed June 27, 2013).
• Rape, Abuse & Incest National Network. “How often does sexual assault occur?” RAINN, 2009. Available online at www.rainn.org/get-information...sexual-assault (accessed June 27, 2013).