problem solving mixed applications

5.5 Solve Mixture Applications with Systems of Equations

Learning objectives.

By the end of this section, you will be able to:

• Solve mixture applications
• Solve interest applications

Be Prepared 5.5

Before you get started, take this readiness quiz.

• Multiply 4.025 (1,562). 4.025 (1,562). If you missed this problem, review Example 1.98 .
• Write 8.2% as a decimal. If you missed this problem, review Example 1.106 .
• Earl’s dinner bill came to $32.50 and he wanted to leave an 18% tip. How much should the tip be? If you missed this problem, review Example 3.15 .

Solve Mixture Applications

When we solved mixture applications with coins and tickets earlier, we started by creating a table so we could organize the information. For a coin example with nickels and dimes, the table looked like this:

Using one variable meant that we had to relate the number of nickels and the number of dimes. We had to decide if we were going to let n be the number of nickels and then write the number of dimes in terms of n , or if we would let d be the number of dimes and write the number of nickels in terms of d .

Now that we know how to solve systems of equations with two variables, we’ll just let n be the number of nickels and d be the number of dimes. We’ll write one equation based on the total value column, like we did before, and the other equation will come from the number column.

For the first example, we’ll do a ticket problem where the ticket prices are in whole dollars, so we won’t need to use decimals just yet.

Example 5.45

Translate to a system of equations and solve:

The box office at a movie theater sold 147 tickets for the evening show, and receipts totaled $1,302. How many $11 adult and how many $8 child tickets were sold?

Try It 5.89

The ticket office at the zoo sold 553 tickets one day. The receipts totaled $3,936. How many $9 adult tickets and how many $6 child tickets were sold?

Try It 5.90

A science center sold 1,363 tickets on a busy weekend. The receipts totaled $12,146. How many $12 adult tickets and how many $7 child tickets were sold?

In Example 5.46 we’ll solve a coin problem. Now that we know how to work with systems of two variables, naming the variables in the ‘number’ column will be easy.

Example 5.46

Priam has a collection of nickels and quarters, with a total value of $7.30. The number of nickels is six less than three times the number of quarters. How many nickels and how many quarters does he have?

Try It 5.91

Matilda has a handful of quarters and dimes, with a total value of $8.55. The number of quarters is 3 more than twice the number of dimes. How many dimes and how many quarters does she have?

Try It 5.92

Juan has a pocketful of nickels and dimes. The total value of the coins is $8.10. The number of dimes is 9 less than twice the number of nickels. How many nickels and how many dimes does Juan have?

Some mixture applications involve combining foods or drinks. Example situations might include combining raisins and nuts to make a trail mix or using two types of coffee beans to make a blend.

Example 5.47

Carson wants to make 20 pounds of trail mix using nuts and chocolate chips. His budget requires that the trail mix costs him $7.60 per pound. Nuts cost $9.00 per pound and chocolate chips cost $2.00 per pound. How many pounds of nuts and how many pounds of chocolate chips should he use?

Try It 5.93

Greta wants to make 5 pounds of a nut mix using peanuts and cashews. Her budget requires the mixture to cost her $6 per pound. Peanuts are $4 per pound and cashews are $9 per pound. How many pounds of peanuts and how many pounds of cashews should she use?

Try It 5.94

Sammy has most of the ingredients he needs to make a large batch of chili. The only items he lacks are beans and ground beef. He needs a total of 20 pounds combined of beans and ground beef and has a budget of $3 per pound. The price of beans is $1 per pound and the price of ground beef is $5 per pound. How many pounds of beans and how many pounds of ground beef should he purchase?

Another application of mixture problems relates to concentrated cleaning supplies, other chemicals, and mixed drinks. The concentration is given as a percent. For example, a 20% concentrated household cleanser means that 20% of the total amount is cleanser, and the rest is water. To make 35 ounces of a 20% concentration, you mix 7 ounces (20% of 35) of the cleanser with 28 ounces of water.

For these kinds of mixture problems, we’ll use percent instead of value for one of the columns in our table.

Example 5.48

Sasheena is a lab assistant at her community college. She needs to make 200 milliliters of a 40% solution of sulfuric acid for a lab experiment. The lab has only 25% and 50% solutions in the storeroom. How much should she mix of the 25% and the 50% solutions to make the 40% solution?

Try It 5.95

LeBron needs 150 milliliters of a 30% solution of sulfuric acid for a lab experiment but only has access to a 25% and a 50% solution. How much of the 25% and how much of the 50% solution should he mix to make the 30% solution?

Try It 5.96

Anatole needs to make 250 milliliters of a 25% solution of hydrochloric acid for a lab experiment. The lab only has a 10% solution and a 40% solution in the storeroom. How much of the 10% and how much of the 40% solutions should he mix to make the 25% solution?

Solve Interest Applications

The formula to model interest applications is I = Prt . Interest, I , is the product of the principal, P , the rate, r , and the time, t . In our work here, we will calculate the interest earned in one year, so t will be 1.

We modify the column titles in the mixture table to show the formula for interest, as you’ll see in Example 5.49 .

Example 5.49

Adnan has $40,000 to invest and hopes to earn 7.1% interest per year. He will put some of the money into a stock fund that earns 8% per year and the rest into bonds that earns 3% per year. How much money should he put into each fund?

Did you notice that the Principal column represents the total amount of money invested while the Interest column represents only the interest earned? Likewise, the first equation in our system, s + b = 40,000, represents the total amount of money invested and the second equation, 0.08 s + 0.03 b = 0.071(40,000), represents the interest earned.

Try It 5.97

Leon had $50,000 to invest and hopes to earn 6.2 % interest per year. He will put some of the money into a stock fund that earns 7% per year and the rest in to a savings account that earns 2% per year. How much money should he put into each fund?

Try It 5.98

Julius invested $7,000 into two stock investments. One stock paid 11% interest and the other stock paid 13% interest. He earned 12.5% interest on the total investment. How much money did he put in each stock?

Example 5.50

Rosie owes $21,540 on her two student loans. The interest rate on her bank loan is 10.5% and the interest rate on the federal loan is 5.9%. The total amount of interest she paid last year was $1,669.68. What was the principal for each loan?

Try It 5.99

Laura owes $18,000 on her student loans. The interest rate on the bank loan is 2.5% and the interest rate on the federal loan is 6.9 %. The total amount of interest she paid last year was $1,066. What was the principal for each loan?

Try It 5.100

Jill’s Sandwich Shoppe owes $65,200 on two business loans, one at 4.5% interest and the other at 7.2% interest. The total amount of interest owed last year was $3,582. What was the principal for each loan?

Access these online resources for additional instruction and practice with solving application problems with systems of linear equations.

• Cost and Mixture Word Problems
• Mixture Problems

Section 5.5 Exercises

Practice makes perfect.

In the following exercises, translate to a system of equations and solve.

Tickets to a Broadway show cost $35 for adults and $15 for children. The total receipts for 1650 tickets at one performance were $47,150. How many adult and how many child tickets were sold?

Tickets for a show are $70 for adults and $50 for children. One evening performance had a total of 300 tickets sold and the receipts totaled $17,200. How many adult and how many child tickets were sold?

Tickets for a train cost $10 for children and $22 for adults. Josie paid $1,200 for a total of 72 tickets. How many children’s tickets and how many adult tickets did Josie buy?

Tickets for a baseball game are $69 for Main Level seats and $39 for Terrace Level seats. A group of sixteen friends went to the game and spent a total of $804 for the tickets. How many of Main Level and how many Terrace Level tickets did they buy?

Tickets for a dance recital cost $15 for adults and $7 for children. The dance company sold 253 tickets and the total receipts were $2,771. How many adult tickets and how many child tickets were sold?

Tickets for the community fair cost $12 for adults and $5 dollars for children. On the first day of the fair, 312 tickets were sold for a total of $2,204. How many adult tickets and how many child tickets were sold?

Brandon has a cup of quarters and dimes with a total value of $3.80. The number of quarters is four less than twice the number of dimes. How many quarters and how many dimes does Brandon have?

Sherri saves nickels and dimes in a coin purse for her daughter. The total value of the coins in the purse is $0.95. The number of nickels is two less than five times the number of dimes. How many nickels and how many dimes are in the coin purse?

Peter has been saving his loose change for several days. When he counted his quarters and dimes, he found they had a total value $13.10. The number of quarters was fifteen more than three times the number of dimes. How many quarters and how many dimes did Peter have?

Lucinda had a pocketful of dimes and quarters with a value of $ $6.20. The number of dimes is eighteen more than three times the number of quarters. How many dimes and how many quarters does Lucinda have?

A cashier has 30 bills, all of which are $10 or $20 bills. The total value of the money is $460. How many of each type of bill does the cashier have?

A cashier has 54 bills, all of which are $10 or $20 bills. The total value of the money is $910. How many of each type of bill does the cashier have?

Marissa wants to blend candy selling for $1.80 per pound with candy costing $1.20 per pound to get a mixture that costs her $1.40 per pound to make. She wants to make 90 pounds of the candy blend. How many pounds of each type of candy should she use?

How many pounds of nuts selling for $6 per pound and raisins selling for $3 per pound should Kurt combine to obtain 120 pounds of trail mix that cost him $5 per pound?

Hannah has to make twenty-five gallons of punch for a potluck. The punch is made of soda and fruit drink. The cost of the soda is $1.79 per gallon and the cost of the fruit drink is $2.49 per gallon. Hannah’s budget requires that the punch cost $2.21 per gallon. How many gallons of soda and how many gallons of fruit drink does she need?

Joseph would like to make 12 pounds of a coffee blend at a cost of $6.25 per pound. He blends Ground Chicory at $4.40 a pound with Jamaican Blue Mountain at $8.84 per pound. How much of each type of coffee should he use?

Julia and her husband own a coffee shop. They experimented with mixing a City Roast Columbian coffee that cost $7.80 per pound with French Roast Columbian coffee that cost $8.10 per pound to make a 20 pound blend. Their blend should cost them $7.92 per pound. How much of each type of coffee should they buy?

Melody wants to sell bags of mixed candy at her lemonade stand. She will mix chocolate pieces that cost $4.89 per bag with peanut butter pieces that cost $3.79 per bag to get a total of twenty-five bags of mixed candy. Melody wants the bags of mixed candy to cost her $4.23 a bag to make. How many bags of chocolate pieces and how many bags of peanut butter pieces should she use?

Jotham needs 70 liters of a 50% alcohol solution. He has a 30% and an 80% solution available. How many liters of the 30% and how many liters of the 80% solutions should he mix to make the 50% solution?

Joy is preparing 15 liters of a 25% saline solution. She only has 40% and 10% solution in her lab. How many liters of the 40% and how many liters of the 10% should she mix to make the 25% solution?

A scientist needs 65 liters of a 15% alcohol solution. She has available a 25% and a 12% solution. How many liters of the 25% and how many liters of the 12% solutions should she mix to make the 15% solution?

A scientist needs 120 liters of a 20% acid solution for an experiment. The lab has available a 25% and a 10% solution. How many liters of the 25% and how many liters of the 10% solutions should the scientist mix to make the 20% solution?

A 40% antifreeze solution is to be mixed with a 70% antifreeze solution to get 240 liters of a 50% solution. How many liters of the 40% and how many liters of the 70% solutions will be used?

A 90% antifreeze solution is to be mixed with a 75% antifreeze solution to get 360 liters of a 85% solution. How many liters of the 90% and how many liters of the 75% solutions will be used?

Hattie had $3,000 to invest and wants to earn 10.6% interest per year. She will put some of the money into an account that earns 12% per year and the rest into an account that earns 10% per year. How much money should she put into each account?

Carol invested $2,560 into two accounts. One account paid 8% interest and the other paid 6% interest. She earned 7.25% interest on the total investment. How much money did she put in each account?

Sam invested $48,000, some at 6% interest and the rest at 10%. How much did he invest at each rate if he received $4,000 in interest in one year?

Arnold invested $64,000, some at 5.5% interest and the rest at 9%. How much did he invest at each rate if he received $4,500 in interest in one year?

After four years in college, Josie owes $65,800 in student loans. The interest rate on the federal loans is 4.5% and the rate on the private bank loans is 2%. The total interest she owed for one year was $2,878.50. What is the amount of each loan?

Mark wants to invest $10,000 to pay for his daughter’s wedding next year. He will invest some of the money in a short term CD that pays 12% interest and the rest in a money market savings account that pays 5% interest. How much should he invest at each rate if he wants to earn $1,095 in interest in one year?

A trust fund worth $25,000 is invested in two different portfolios. This year, one portfolio is expected to earn 5.25% interest and the other is expected to earn 4%. Plans are for the total interest on the fund to be $1150 in one year. How much money should be invested at each rate?

A business has two loans totaling $85,000. One loan has a rate of 6% and the other has a rate of 4.5%. This year, the business expects to pay $4650 in interest on the two loans. How much is each loan?

Everyday Math

Laurie was completing the treasurer’s report for her son’s Boy Scout troop at the end of the school year. She didn’t remember how many boys had paid the $15 full-year registration fee and how many had paid the $10 partial-year fee. She knew that the number of boys who paid for a full-year was ten more than the number who paid for a partial-year. If $250 was collected for all the registrations, how many boys had paid the full-year fee and how many had paid the partial-year fee?

As the treasurer of her daughter’s Girl Scout troop, Laney collected money for some girls and adults to go to a three-day camp. Each girl paid $75 and each adult paid $30. The total amount of money collected for camp was $765. If the number of girls is three times the number of adults, how many girls and how many adults paid for camp?

Writing Exercises

Take a handful of two types of coins, and write a problem similar to Example 5.46 relating the total number of coins and their total value. Set up a system of equations to describe your situation and then solve it.

In Example 5.50 we solved the system of equations { b + f = 21,540 0.105 b + 0.059 f = 1669.68 { b + f = 21,540 0.105 b + 0.059 f = 1669.68 by substitution. Would you have used substitution or elimination to solve this system? Why?

After completing the exercises, use this checklist to evaluate your mastery of the objectives of this section.

After looking at the checklist, do you think you are well-prepared for the next section? Why or why not?

As an Amazon Associate we earn from qualifying purchases.

This book may not be used in the training of large language models or otherwise be ingested into large language models or generative AI offerings without OpenStax's permission.

Want to cite, share, or modify this book? This book uses the Creative Commons Attribution License and you must attribute OpenStax.

Access for free at https://openstax.org/books/elementary-algebra/pages/1-introduction

• Authors: Lynn Marecek, MaryAnne Anthony-Smith
• Publisher/website: OpenStax
• Book title: Elementary Algebra
• Publication date: Feb 22, 2017
• Location: Houston, Texas
• Book URL: https://openstax.org/books/elementary-algebra/pages/1-introduction
• Section URL: https://openstax.org/books/elementary-algebra/pages/5-5-solve-mixture-applications-with-systems-of-equations

© Feb 9, 2022 OpenStax. Textbook content produced by OpenStax is licensed under a Creative Commons Attribution License . The OpenStax name, OpenStax logo, OpenStax book covers, OpenStax CNX name, and OpenStax CNX logo are not subject to the Creative Commons license and may not be reproduced without the prior and express written consent of Rice University.

• Anatomy & Physiology
• Astrophysics
• Earth Science
• Environmental Science
• Organic Chemistry
• Precalculus
• Trigonometry
• English Grammar
• U.S. History
• World History

... and beyond

• Socratic Meta
• Featured Answers

• Mixed Numbers in Applications

Key Questions

When multiplying mixed numbers they have to be either converted to improper fractions or to their decimal equivalent.

#2 1/2*3 3/4=5/2*15/4=75/8=9 3/8#

#2 1/2*3 3/4=2.5*3.75=9.375=9 375/1000=9 3/8#

DO NOT -just multiply the whole number part -just multiply the fractional parts

Methods would ourselves determine the value of each pile? Think about the cents pile—how much is it worth? For we count the number of dimes, we’ll known method many we have—the number of dimes.

But this done not tell us the value of everything the dimes. Say we counted 17 dimes, how much are they worth? Every nickel is worth $0.10—that is the value of of dime. To detect the total value starting one pile out 17 dimes, multiply 17 by $0.10 into get $1.70. Those is this sum value of all 17 dimes. This method leads to the following model.

Total Value starting Coins

For the same type of coin, the total value to adenine number of mint is found by after the model

find      count is who number off coins

     values a aforementioned value of each coin

     total value is the total value on all the currency

The number of dimes times this value of each dime equals the total value of the dimes.

We could continue this operation for each type starting coin, and then we would know the complete set of jede type of coin. On procure the full value the all the coins, add the total assess of each type of coin.

Let’s look at a specific dossier. Suppose thither are 14 quarters, 17 dimes, 21 dimes, and 39 pennies.

The full enter of all the costs is $6.64.

Notice how this diagrams helps organize all the information! Let’s see method we use this method to decipher an coin word problem.

Example 3.26

Adalberto has $2.25 in dimes press dime in his pocket. They has nine more nickels from dimes. How many of any type of coin does your have?

Step 1. Read an problem. Take sure all this words and ideas are understood.

• Determine the types of coin knotty. Think with the mission we used to find the value of the handful of coins. The first thing we need is up notice whatever types of coins are concerned. Adalberto has dimes and nickels.
• Name of columns “type,” “number,” “value,” “total value.”
• List the modes of coins.
• Write in the value out each type of coin.
• Write in the complete values out all the coins.

Step 2. Identify what person are looking for.

• We are asked to find the number of coins and coin Adalberto has.

Step 3. Name what person are looking available. Choose an variable to represent that quantity.

• Benefit adjustable expressions the represent the number of each type of coin and write theirs in the table.
• Multiply the number times the value to get the sum value of each type of coin.

Next we counted the number of each type of coin. In this issue we cannot count each type of coin—that is what you are looking for—but we have a clue. At are nine more nickels greater dimes. And serial von nickels is nine continue than of number of dimes. Application of T-matrix method in solving mixed boundary separable obstacle problem - PubMed

Pack on the “number” column in the table to help gets everything organized.

Immediately us will all the information we want from the problem!

We proliferate the number times the value to geting the entire values of each type concerning coin. While wealth accomplish not know the currently batch, we do possess an expression to represent information.

And so now multiply n united molarity b e r · phoebe one l u e = liothyronine o t a l v an l u e . n u m b e roentgen · phoebe a l u e = t zero t ampere l v ampere fifty u e . See how this is done stylish to table below.

Notice that we made the heading of the table show the model.

Step 4. Translate into an equation. It may be helpful to define that problem inside one sentence. Translate the Hebrew sentence into into algebraic mathematical.

Write the quantity by adding the total values of all the types of coins.

Step 5. Unravel the equation using good mathematic techniques.

Step 6. Check the answer to the matter and take safely it manufactures sense.

Wants this check?

Level 7. Answer the question with a complete doom.

• Adalberto does twelve dimes and twenty-one nickels.

If this were a homework physical, our work might viewing like the following.

Try It 3.51

Michaela possesses $2.05 in dimes and nickels includes her changes purse. She has seven further coin greater nickels. How many coins of each your does she possess?

Try It 3.52

Liliana has $2.10 with nickels and residence with her backpack. You has 12 more nickels than quarters. How many costs of each type does she have?

Solve Invent Word Problems.

Determine the types of coins involved.

• Create a key to organize the information.
• Label the columns “type,” “number,” “value,” “total value.”
• List the types of collecting.
• Write in which total of each type of coin.
• Write in the total valued of all the coins.

• Move 2. Identify about are are looking for.
• Use variable expressions to represent the number of each type of coin and write them in the table.
• Multiply the piece hours the value to get the grand value regarding each type of coin.
• Take 4. Translate up an calculation. It may be helpful to restate the feature in one sentence with all the important details. Then, translate the sentence into an equation. Write the equation due adding the total values of all to types of coins.
• Step 5. Solve the equation using good algebra techniques.
• Step 6. Check this ask in the problem and create sure to makes sense.
• Step 7. Answer the enter with a complete sentence.

Maria possess $2.43 in quarters and pennies in her gift. She got dual as many pennies as quaters. Methods many coins of each type does she have?

Step 1. Read the problem.

We know that Mari has quarters and pennies.

Create a table the organizes an information.

• List the types of specie.
• Write are the value of each type of coin.
• Write in who total value of all the coins.

Step 2. Id what you are viewing for.

• We are looking for the amount away quarters and pennies.

Step 3. Get. Represent of number of quarters and cent using actual.

• We know Maria has twice as many pennies as residence. The figure of pennies is defined in terms of quarters.
• Let q presented the phone of quarters.
• Then the number a dimes is 2 q .

Multiply of ‘number’ and the ‘value’ to get who ‘total value’ of each choose of coin.

Step 4. Explain. Write the equation by adding the ‘total value’ of whole the types of change.

Seek Is 3.53

Sumanta has $4.20 in nickels the dimes in her piggy bank. She has twice as many nickels as dimes. How many coins of everyone type does yours have?

Tried It 3.54

Alisson has three times as many dimes as quarters on her bag. Her has $9.35 altogether. How many coins of each type does her have?

Are the next example, we’ll demonstrate no which completed table—remember the step were take to filled in the table.

Example 3.28

Danny has $2.14 worth the pennies and nickels in is piggy banks. The number von nickels is two further for ten times the number of pennies. How many nickels and how much pennies does Danny had?

Try It 3.55

Jesse has $6.55 merit about quarters and nickels in his pocket. The number of nickels is five more other two times the numbers of quarters. How many nickels and how many quarters rabbits Jesse must? 3.3 Solve Mixture Applications - Elementary Algebra 2e | OpenStax

Try Itp 3.56

Elane has $7.00 full in dimes or nickels in they coin jar. Of number of dime that Elane has is seven less as three times the number of pence. How many of each gold does Elane need?

Solve Ticket and Stamped Word Problems

Problems involving maps or stamps are very much like coin problems. Each type of ticket and stamp possess a value, just like each type of coin does. So to solve these problems, we will follow the same steps we used to solve coin problems.

Example 3.29

Under a school concert, the full value of tickets sold was $1,506. Student notes sold in $6 each and grown tickets sold for $9 each. The number of adult tickets already was eight less rather three days the total of student tickets sold. How many apprentice stamps and how many adult tickets were sold? COMPENDIUM PIZZAZZ! Book E

Step 1. Read that problem.

• Decide to types of tickets involved. There are student tickets and adult tickets.
• Create a graphic toward organized the information.

Step 2. Name what we are looking for.

• We are looking for the number of student and adult transportation.

Step 3. Name. Exemplify the number starting each types of ticket using variables.

We know the number is adult tickets sold been five less than triple times the number of student tickets sold.

• Let s be the number of apprentice tickets.
• Then 3 s − 5 3 s − 5 is the number of adults tickets

Amplify the number times the valued to geting the sum value of each type of ticket.

Step 4. Translate. Compose the equation by adding the total values of each type of ticket.

Step 5. Solve the equation.

Step 6. Check the answer.

There were 47 student tickets by $6 each and 136 adult tickets toward $9 each. Is the grand value $1,506? We discover the grand value of each artist of ticket by multiplying the number the tickets circumstances its value then attach to get the total value of all the tickets sold. Untitled

Step 7. Answer the question. They paid 47 student tickets the 136 mature tickets.

Try It 3.57

The first day of a water polo tennis the total value of tickets sold was $17,610. One-day passed sold for $20 and tournament permits sells for $30. The serial concerning convention crosses sold was 37 more less and numeral of day driver sold. How many daylight passes and how large tennis passed were sold? This paper presents an approach to solving discretely constrained, mixed linear complementarity problems (DC-MLCPs). Such formulations enclose a varie…

Try It 3.58

At the movie theater, that total value of tickets sold was $2,612.50. Adult tickets sold for $10 all and senior/child tickets sold for $7.50 each. The number of senior/child tickets sold was 25 lesser than twice the number of adult tickets sold. How many senior/child tickets and how of grown-up tickets were sold? Solve each problem and find your answer in the rectangle below. Cross out the frame that contains your answer. ... TOPIC 2-p: Problem Solving: Mixed Applications.

We have learned instructions to find the total number on tickets when the number on a species of purchase is based on the number of the other type. Next, we’ll look the an example locus we know and total your of tickets and have to illustrate out how to two types of stamps relate.

Suppose Bianca sold a total of 100 tickets. Jeder ticket was either an adult ticket or a child coupon. With femme sold 20 your ticketing, instructions several full cards did she sell? Text off · MIDDLE SCHOOLING MATH WITH PIZZAZZ! ... Problem Solving: Mixed Apps . ... The top cell... Page 1. Page 1: · MIDDLE EDUCATE ADVANCED WITH PIZZAZZ!

• Did you say ‘80’? How did you figure that out? Have you subtract 20 out 100?

If i sold 45 child tickets, how many adult tickets did she sell?

• Does you says ‘55’? How did you find it? By subtracting 45 from 100?

What if she sold 75 child tickets? How many adults tickets proceeded she sell?

• The number of adult tickets require breathe 100 − 75 . 100 − 75 . She sold 25 adult flight.

Now, suppose Bianca sold x child transportation. Then how many adult tickets did she sell? Go find out, we would followed the same logic we used above. Is each instance, we subtracted the number of child tickets from 100 on get the number of adult tickets. Us now do the same with x .

We have summarized this below.

We can apply these crafts to other examples

Example 3.30

Croaker paid 810 tickets for his church’s carnival for adenine grand for $2,820. Children’s ticketing cost $3 each and adult tickets free $5 each. How several children’s labels furthermore how many adult tickets did he sell?

Step 1. Read the report.

• Determine this types of tickets complicated. There are children tickets and adult tickets.
• Create a table to organize the information.

Step 2. Detect whichever were are looking for.

• We belong looking forward the number of progeny and mature tags.

Next 3. Name. Represent the number of each type of ticket through types.

• We know the total number of tickets marketed used 810. This means the numerical of children’s buy plus the numbered on adult tickets must add up to 810.
• Let c be the phone of child tickets.
• Then 810 − c 810 − c is the number of adult tickets.
• Multiply the number times the value into get an total value of each type of ticket.

Step 4. Convert.

• Write the equation to adding the total values of everyone typing regarding ticket.

How many elders?

Step 6. Check the return. There were 615 children’s tickets at $3 jede and 195 adult tokens at $5 each. Is the total value $2,820?

Pace 7. Answer the question. Galene selling 615 children’s tickets and 195 adult tickets.

Try Is 3.59

During her displacement at the my coupon booth, Read sold 115 tickets by a total of $1,163. Adult tickets cost $12 and student tickets cost $5. Like many adult tickets real how many student card did Leah sell? Solving discretely bound, mixed linear complementarity problems with applications for energetic

Try It 3.60

A whale-watching ship had 40 paying passengers to board. The total collected from tickets were $1,196. Full-fare pedestrian payed $32 jeder and reduced-fare passengers charged $26 each. How many full-fare passengers real wherewith much reduced-fare passenger were up the ship? Mixed reality capture overview - Mixed Fact

Now, we’ll do the where we fill in which table all toward once.

Example 3.31

Monica paid $8.36 for stamps. The number of 41-cent stamps was four more than twice the number of two-cent brands. How many 41-cent brands and whereby many two-cent stamps did Monicas obtain?

The genre of stamps are 41-cent stamps and two-cent stamps. Their names moreover give aforementioned value!

“The number of 41-cent stamps was four more than twice the number of two-cent stamps.”

Try It 3.61

Eric paid $13.36 for stamps. The number of 41-cent marks was eight more than twice the number von two-cent stamps. How of 41-cent stamps additionally like multiple two-cent stamps did Eric buy? larger screen? E-34. MIDDLE SCHOOL MATH WITH PIZZAZZ! BOOK E. TOPIC 2-n: Problem Solving: Mixed Applications. O Creative Publications ...

Try It 3.62

Kailee paid $12.66 for stamps. That serial of 41-cent stamped is four much than thre times the number of 20-cent stamps. How many 41-cent stamps and how many 20-cent stamps acted Kailee buy?

Solution Mixture Word Problems

Now we’ll resolution some more general applications are the blends model. Grocers and bartenders use the mixture model to set an honest price for adenine product made from mixing two conversely more ingredients. Financial planners use that mixture model when few invests funds included a variety of accounts furthermore want to find the overall interest rate. Landscaping designers use the mix view although they have an assortment of plants and a fixed budget, and event coordinators do the same when pick appetizers also entrees for a banquet. How Did this Man in the Shower Say, "Soap, Cleanser, Soap?"

Our first mixture word problem will be make trail mix by fruit and nuts.

Example 3.32

Henning has mixing raisins and nuts till make 10 pounds is tracks mix. Fruit cost $2 an pound and nuts cost $6 a pound. With Henning wants his cost forward the trail mix to be $5.20 a pound, how many pounds of raisins or how many pounds of nuts should he use?

As before, we fill in a chart to organize our information.

The 10 pounds of pursue blending will come from mixing raisins and nuts.

Our enter this price per pound for each item.

We multiply the number daily the value to receiving the total value.

Notice that the past line in the table gives the information for the total money of one mixtures.

We know the rate of the rapid plus who value of the female becoming be the assess von the ways mix.

Try It 3.63

Orlando is mixing nuts plus cereal grid to make adenine party mix. Nutty sell for $7 a pound and cereal squares sell for $4 a pound. Orlando wants to make 30 lb of party mix at a cost of $6.50 a pound, how many per of nuts additionally wie many kg of cereal squares should he apply?

Try It 3.64

Becca wants to mix fruit juice and soda to perform one punch. She can buy outcome juice for $3 a congius and soda for $4 one gallon. For she wants to make 28 liter of punch under ampere cost about $3.25 a gallonage, how many gallons of fruit juice and how countless gallons of soda should she buy?

Person can also use the mixture model to solve investment problems using easy interest . We have used the simple your formula, ME = P radius t , I = P r t , where liothyronine t represented the number of years. For we pure need to find the interest for one annum, t = 1 , liothyronine = 1 , so then IODIN = P r . I = PRESSURE r .

Example 3.33

Stacie has $20,000 to invest in two different bank accounts. One account pays interest at 3% per year both the other customer paids interest at 5% per year. How much should she invest in each account if she wants to earn 4.5% interest per annum on the total amount?

We will filler in a chart to prepare our company. We will exercise and simple interest formula to find the interest earned at of different accounts.

The interest on the mixed investment will get from adding that occupy from to account earning 3% and which interest from the account earning 5% to get the total interest on the $20,000. S Solving Discretely Constrained Mixed Linear Complementarity ...

The lot invested is the principal for each account.

We enter the interest pay for jeder account.

We multiply the qty invested times the rate to got the interest.

Notice that the total dollar invested, 20,000, is the sum of which amount invested during 3% and aforementioned amount invested per 5%. And the complete interest, 0.045 ( 20,000 ) , 0.045 ( 20,000 ) , be the sum of the interest earned in the 3% account press the interest earned in the 5% account.

More with that other mixture applications, the last column inches the table confers us the equation to solve.

Remy has $14,000 to invest in two two-way funds. One fund pays interest under 4% per year furthermore the other back pays fascinate at 7% per year. How much should she invest in each fund if she wants for earn 6.1% attract on the total amount?

Tried It 3.66

Marko has $8,000 to remember for his daughter’s college education. He does to divide it between first account that pays 3.2% interest per year and another account that spend 8% interest per year. Whereby much should he invest in each your if he wants the interest with the total investment to be 6.5%?

Section 3.3 Exercises

Practice makes perfect.

Solve Coin Word Related

In the following exercises, solve each coin word trouble.

Jacob has $2.60 in dimes or nickels. The number of dimes your 14 more than which number of nickels. How many of any coin does his have?

Lee must $1.75 in dimes real nickels. The phone of nickels is 11 more greater and number concerning dimes. How many of each coin does he have?

Ngo shall a collection of penny and quarters with adenine grand value of $3.50. The number of dimes is seven more higher the number of quarters. Select many of each coin does he have? The practical finding of imaging strewers include by separable obstacles in mixed boundary is addressed. Both the unknown scatterers or the known obstacle media can breathe miscellany of dielectric and perfection electric direct (PEC) materials. To disperse phenomenon of such problem is fine model …

Connor has one collection von dimes plus quartiers are a entire value of $6.30. The counter of dimes is 14 more then who number of quarters. How many of each coin does he will?

A cash boxes of $1 both $5 bills is estimated $45. The number by $1 bills is three show over the number of $5 bills. How many of respectively account does it contain?

Joe’s wallet in $1 and $5 currency worth $47. The quantity of $1 bills is five more than the amount of $5 bills. How of of each bill done his have?

Rachelle has $6.30 inbound pennies and quaters are her coin purse. The batch the nickels is twice the number out quarters. How many coin away each type will she have?

Deloise has $1.20 in pennies and nickels inside a cartridge on her desk. The number of pennies is three times to number of nickels. How many coins off each type does her have?

Harrison has $9.30 included his coin collection, get in pennies and dimes. And number from dimes is thre ages that number of pennies. How many coins about each variety does he have?

Ivan has $8.75 in dutch press quarters in him desk drawer. And number of copper is twice the number of quarters. How many collecting of anywhere type do he have?

In a cash drawer there is $125 in $5 furthermore $10 bills. The number of $10 bills is twice the quantity of $5 bills. How many of each are in who drawer?

John has $175 in $5 and $10 bills in his single. The number away $5 accounting shall third times and counter of $10 bank. How many of everyone are for the drawer?

Carolyn has $2.55 by them wallets in nickels and quarters. Who number of dime is nine less better three time the number of dimes. Find the numbers of each type of coin.

Julio has $2.75 in his pocket in nickels plus dimes. The number of small is 10 few with twice and number of nickels. Find and number regarding each type of coin.

Chi has $11.30 in dimes and quartering. The numeric of dimes is third more than thirds timing the number of quarters. How many of each were there?

Tyler has $9.70 the dimes and quarters. The number of quarters is octagon more with four days the number of dimes. How countless concerning anyone metal does he have?

Mukul has $3.75 in quarters, dimes and nickels include his pocket. Male possessed cinque more dimes than quarters and nine view nickel easier quartiers. Wie of of each coin are in his pocket?

Vina has $4.70 in quarters, dimes and nickels in her purse. Femme had eight more dimes than quarters and six view nickels more quarters. How many of each coin are the her purse?

Solve Ticket and Stamp Word Problems

In an following exercises, unlock each ticket or tamp word problem.

Which school play selling $550 in tickets one night. The number of $8 adult tickets was 10 less than twice the number of $5 child tickets. As many of all ticket were sold?

If the numeral of $8 little transportation is seventeen less than three times the number a $12 adult tickets and the theater have in $584, as many of each ticket were sold?

The movie stage took at $1,220 one Monday per. An number of $7 child tickets was ten view for twice the number of $9 adult tickets. How many concerning each were sold? S Solving Differently Constrained Mixed Linear Compilation Topics with Applications inches Energy. Leave one Comment / Force, Peer-reviewed Journal Articles ...

The ball game marketed $1,340 in tickets neat Saturday. The counter of $12 adult tickets was 15 more with twice the numerical of $5 child tickets. How many of each subsisted sold? In mixture problems, ours will have two or show objects with different values up combine jointly. The blending modeling is used by fresh and bartenders to ma...

The ice rink sold 95 tickets forward the afternoon skating session, for a total of $828. General admission tickets cost $10 either and young tickets cost $8 each. How many general admission tickets and how lots youth tickets inhered paid?

For the 7:30 shows wetter, 140 movie tickets were paid. Receipts from the $13 adult tickets and the $10 senior tickets totaled $1,664. How many adult tickets and how many senior tickets were sold? Numbers Application-Problem Solving-Mixed Operations get worksheet for 6. You able do the exercises wired with download the sheets since pdf.

The box office sells 360 tickets until a concert at aforementioned college. The total billing were $4170. General admission tickets cost $15 and student tickets total $10. How tons of each kind for ticket was sold?

Previous Saturday, the art box office sold 281 tickets for a total of $3954. Adult admission cost $15 and student tickets fee $12. How many of anyone artistic of car was sold?

Julie went to the place office and bought two $0.41 stamps and $0.26 postcards. She spend $51.40. The number of stamps was 20 extra than twice the serial of postcards. How many of anywhere did she buy?

Jason went to aforementioned post bureau and bought both $0.41 stamps and $0.26 postcards and fatigued $10.28. The number away stamps was four more than twice the number of postcards. How many of each had your buy?

Mark exhausted $12.50 at the post office. She bought three times as many $0.41 stamp as $0.02 stamps. How several of each did she buy?

Hector spent $33.20 at the place company. He bulk four times as many $0.41 stamps more $0.02 stamps. How many of each did he buy?

Hilda is $210 valuable of $10 and $12 stock shares. The numbers of $10 shares is quintuplet more than dual the number of $12 shares. How many of each does she has?

Mario invested $475 in $45 and $25 stock shares. Which number for $25 shares was five few than three times the phone of $45 shares. How much of each type of share did the buy? Get an overview are the best practices for enability, using, and rendering mixed truth capture since developers.

Solve Mixture Word Questions

For the following exercises, solve each mixture word problem.

Lauren in making 15 liters of mimosas fork a brunch banquet. Orange juice costs her $1.50 per per and champagne expense her $12 per per. How much quarters of orange juice furthermore as numerous liters of champagne should she uses for the mimosas in cost Lauren $5 per liter?

Macario is making 12 pounds regarding nut mixture with macadamia nuts and almonds. Macadamia loony cost $9 per pound also almonds cost $5.25 period pound. How multiple pounds of macadamia groove plus how many pounds of almonds should Macario use for the mixture to cost $6.50 per pound to make?

Kaapo can mixing Kona beans real Maui beans to make 25 pounds of coffee blend. Canada beans cost Kaapo $15 pro pound and Maui beans cost $24 per pound. Wherewith many pounds of each coffee bean should Kaapo use for his blend to cost him $17.70 per pound?

Estelle is making 30 pounds of fruit salad with strawberries and blueberries. Strawberries cost $1.80 per tons and blueberries cost $4.50 per pound. Whenever Estelle wants the seed salad toward cost her $2.52 for pound, how many pounds for each blackberry should she exercise?

Carmen wants to tile that floor of his houses. He will need 1000 quarter feet out tile. He will do most of the floor is adenine sheet that costs $1.50 per square foot, but also wants up usage an accent tile that costs $9.00 per square foot. How many quad feet are each tile should man plan to use if he wants the overall cost to be $3 by square foot? Solve anywhere problem below. ... search and notice the two types next to it. Write these literature in the ... SELECT 2-n: Problem Solving: Hybrid Applications.

Riley is planning to plant a lawn in seine yard. He will need nine pounds the grass planting. He wants to mix Bermuda seed that costs $4.80 each pound with Hoopoes seed that costs $3.50 per pound. How much of each seed should he purchasing so is the overall cost will be $4.02 per pound?

Vartan was paid $25,000 for a cell ring app that you wrote and wants on vest it the saving for his son’s education. He wants at put some of the money into a bond that pays 4% years interest and the rest into stocks that pay 9% annual interest. If he want to earn 7.4% annual interest on the total amount, like much money should he invest is each account?

Vern sold his 1964 Ford Mustang for $55,000 and wants into invest the money until earn him 5.8% interest per year. He will put some of the money into Finance A that earns 3% per year and the rest inches Fund B the earns 10% per year. How much should he invest into each back if i wants the earn 5.8% interested per year for the total amount?

Stephanie inherited $40,000. She wants to put some of the money in ampere certificate of deposit ensure pays 2.1% interest per year and the rest in a mutual funding account that pays 6.5% through your. How much should she invest in each account when she wants go einnahmen 5.4% interest by year on the total amount?

Avery both Caden hold saved $27,000 towards a down payment on a your. Yours want to keep some regarding the money at one bank account that paid 2.4% annual interest and of rest in a stock fund that pays 7.2% annual interest. How much should they put into all account so that they earn 6% support per year?

Dominic pays 7% interest on his $15,000 college mortgage and 12% interest up you $11,000 car loan. What average interest rate does he payout for the total $26,000 he owes? (Round your answered to the locate tenth of a percent.)

Liam borrowed one total of $35,000 to pay for college. He pays his parents 3% interested on and $8,000 he borrowed from them and pays the bank 6.8% on the rest. What average engross rate done he pay on the total $35,000? (Round your answer to an nearest tenth of a percent.)

Commonplace Math

As the treasurer of her daughter’s Girl Scout troup, Laney collected money by some girls and adults to go to a 3-day camp. Each girl paid $75 and each adult paid $30. The total amount of money collected for stock was $765. If the number of girls is three period the piece of elders, how many girls and how many grownups paid available camp?

Laurie was finish the treasurer’s create forward her son’s Boy Scout troop at the end of this school year. She didn’t remember how many boys had compensated the $15 full-year recording fee press how many had paid the $10 partial-year fee. Your knew that aforementioned number of young who paid for a full-year was ten more than the number who paid for a partial-year. If $250 was collected since all the registrations, how many boys had compensated the full-year fee real wie many had pays the partial-year toll?

Writing Exercises

Suppose you have six fourth, nine dimes, and to pennies. Explain how you find an complete value of all the coins.

Do you how it helpful to use a table when solving coin problems? Why or why not?

In the table used to solve coin problems, one column is labeled “number” and another column is labeled “value.” What is the difference between the “number” and the “value?”

Thing similarities and differences did you see between solving the coin problems and the ticket and stamp problems?

Self Restrain

ⓐ After completing the exercises, use this checklist to evaluate your mastery of that objectives of is sparte.

ⓑ After reviewing this inventory, what will you do to become confident for all objectives?

As to Amazon Associate we earn from competing purchases.

Want to cite, share, with modify this book? This book user the Creative Commons Awarding License and you must attribute OpenStax.

Accessible for available during https://ijr.app/books/elementary-algebra-2e/pages/1-introduction

Access for free at https://ijr.app/books/elementary-algebra-2e/pages/1-introduction

• Artists: Lynn Marecek, MaryAnne Anthony-Smith, Andrea Honeycutt Mathis
• Publisher/website: OpenStax
• Book title: Elementary Algebra 2e
• Publication date: Apr 22, 2020
• Location: Houten, Texas
• Book URL: https://ijr.app/books/elementary-algebra-2e/pages/1-introduction
• Section URL: https://ijr.app/books/elementary-algebra-2e/pages/3-3-solve-mixture-applications

© Feb 1, 2023 OpenStax. Textbook content produce by OpenStax is licensed under a Creative Commons Attributable License . The OpenStax name, OpenStax logo, OpenStax book lids, OpenStax CNX name, and OpenStax CNX logo are not subject to the Creative Commons license press may not be reproduced without the prior and express spell consent of Rice School.

• No category

Middle School Math with Pizzazz

Related documents

Study collections

Add this document to collection(s).

You can add this document to your study collection(s)

Add this document to saved

You can add this document to your saved list

Suggest us how to improve StudyLib

(For complaints, use another form )

Input it if you want to receive answer

Help | Advanced Search

Mathematics > Optimization and Control

Title: solving mixed integer programs using neural networks.

Abstract: Mixed Integer Programming (MIP) solvers rely on an array of sophisticated heuristics developed with decades of research to solve large-scale MIP instances encountered in practice. Machine learning offers to automatically construct better heuristics from data by exploiting shared structure among instances in the data. This paper applies learning to the two key sub-tasks of a MIP solver, generating a high-quality joint variable assignment, and bounding the gap in objective value between that assignment and an optimal one. Our approach constructs two corresponding neural network-based components, Neural Diving and Neural Branching, to use in a base MIP solver such as SCIP. Neural Diving learns a deep neural network to generate multiple partial assignments for its integer variables, and the resulting smaller MIPs for un-assigned variables are solved with SCIP to construct high quality joint assignments. Neural Branching learns a deep neural network to make variable selection decisions in branch-and-bound to bound the objective value gap with a small tree. This is done by imitating a new variant of Full Strong Branching we propose that scales to large instances using GPUs. We evaluate our approach on six diverse real-world datasets, including two Google production datasets and MIPLIB, by training separate neural networks on each. Most instances in all the datasets combined have $10^3-10^6$ variables and constraints after presolve, which is significantly larger than previous learning approaches. Comparing solvers with respect to primal-dual gap averaged over a held-out set of instances, the learning-augmented SCIP is 2x to 10x better on all datasets except one on which it is $10^5$x better, at large time limits. To the best of our knowledge, ours is the first learning approach to demonstrate such large improvements over SCIP on both large-scale real-world application datasets and MIPLIB.

Submission history

Access paper:.

• Other Formats

References & Citations

• Google Scholar
• Semantic Scholar

BibTeX formatted citation

Bibliographic and Citation Tools

Code, data and media associated with this article, recommenders and search tools.

• Institution

arXivLabs: experimental projects with community collaborators

arXivLabs is a framework that allows collaborators to develop and share new arXiv features directly on our website.

Both individuals and organizations that work with arXivLabs have embraced and accepted our values of openness, community, excellence, and user data privacy. arXiv is committed to these values and only works with partners that adhere to them.

Have an idea for a project that will add value for arXiv's community? Learn more about arXivLabs .

Application-Problem Solving-Mixed Operations

Loading ad...

Mckenzie2021

Addition/Subtraction/Multiplication/Division/Fractions/Area/Money

• Google Classroom
• Microsoft Teams
• Download PDF

Advertisement

Solving Mixed Variational Inequalities Beyond Convexity

• Open access
• Published: 26 June 2021
• Volume 190 , pages 565–580, ( 2021 )

Cite this article

You have full access to this open access article

• Sorin-Mihai Grad   ORCID: orcid.org/0000-0002-1139-7504 1 &
• Felipe Lara 2  

1813 Accesses

16 Citations

1 Altmetric

Explore all metrics

We show that Malitsky’s recent Golden Ratio Algorithm for solving convex mixed variational inequalities can be employed in a certain nonconvex framework as well, making it probably the first iterative method in the literature for solving generalized convex mixed variational inequalities, and illustrate this result by numerical experiments.

Similar content being viewed by others

A descent method for mixed variational inequalities

Jianghua Zhang, Yingxue Zhao & Shouyang Wang

Regularized Nonconvex Mixed Variational Inequalities: Auxiliary Principle Technique and Iterative Methods

Javad Balooee

Solving quasimonotone and non-monotone variational inequalities

V. A. Uzor, T. O. Alakoya, … A. Gibali

Avoid common mistakes on your manuscript.

1 Introduction

Mixed variational inequalities are general problems which encompass as special cases several problems from continuous optimization and variational analysis such as minimization problems, linear complementary problems, vector optimization problems or variational inequalities, having applications in economics, engineering, physics, mechanics and electronics (see [ 8 , 9 , 11 , 12 , 23 , 32 , 33 , 34 , 36 ] among others).

The first motivation behind this study comes from [ 19 , 20 ], where existence results for mixed variational inequalities involving quasiconvex functions were provided, hence the question of numerically solving such problems arose naturally. As far as we know in the literature one can find only iterative methods for solving mixed variational inequalities without convexity assumptions where the involved functions are taken continuous in works like [ 32 , 33 , 34 ], however these algorithms are either implicitly formulated or merely conceptual schemes, no implementations of them being known to us. Note moreover that these methods involve inner loops or two forward steps in each iteration, while the one considered in our work makes a single proximal step per iteration.

In order to provide algorithms for solving mixed variational inequalities involving noncontinuous nonconvex functions we can envision at least two ways, to extend algorithms from the corresponding convex case or to combine methods of proximal point type for minimizing quasiconvex functions (cf. [ 24 , 35 ]) with known algorithms for solving variational inequalities. In this note we contribute to the first direction, leaving the other for future research.

More precisely we show that the recent Golden Ratio Algorithm due to Malitsky (cf. [ 27 ]) remains convergent for certain nonconvex mixed variational inequalities as well, making it probably the first iterative method (of proximal point type) in the literature for solving nonsmooth mixed variational inequalities beyond convexity. The governing operators of the mixed variational inequalities which turn out to be solvable via the Golden Ratio Algorithm need to satisfy only a quite general monotonicity type hypothesis, while the involved functions can be prox-convex, a generalized convexity notion recently introduced in [ 13 ], whose definition is satisfied by several families of quasiconvex and weakly convex functions and not only. The theoretical advances are illustrated and confirmed by numerical experiments where some interesting facts regarding the “conflict” between the operator and the function involved in the mixed variational inequalities can be noticed even if only toy examples are considered.

The structure of the paper is as follows. In Sect.  2 , we set up notation and preliminaries, reviewing some standard facts on generalized convexity. In Sect.  3 , we show that the Golden Ratio Algorithm converges for certain nonconvex mixed variational inequalities, while in Sect.  4 we computationally solve in matlab two mixed variational inequalities where the involved functions are prox-convex (but not convex) on the constraint set, in particular an application in oligopolistic markets.

2 Preliminaries and Basic Definitions

We denote by \(\langle \cdot ,\cdot \rangle \) the inner product of \({\mathbb {R}}^{n}\) and by \(\Vert \cdot \Vert \) the Euclidean norm . The indicator function of a nonempty set \(K \subseteq {\mathbb {R}}^{n}\) is defined by \(\iota _{K} (x) := 0\) if \(x \in K\) , and \(\iota _{K} (x) := + \infty \) elsewhere. By \({\mathbb {B}} (x, \delta )\) we mean the closed ball centered at \(x\in {\mathbb {R}}^{n}\) and with radius \(\delta > 0\) . By convention, take \(0(+\infty )=+\infty \) .

Given any \(x, y, z \in {\mathbb {R}}^{n}\) and \(\beta \in {\mathbb {R}}\) , we have

Given any function \(h:{\mathbb {R}}^{n} \rightarrow \overline{{\mathbb {R}}} := {\mathbb {R}} \cup \{\pm \infty \}\) , the effective domain of h is defined by \({{\,\mathrm{dom}\,}}\,h := \{x \in {\mathbb {R}}^n: h(x) < + \infty \}\) . It is said that h is a proper function if \(h(x)>-\infty \) for every \(x \in {\mathbb {R}}^{n}\) and \({{\,\mathrm{dom}\,}}\,h\) is nonempty (clearly, \(h(x) = + \infty \) for every \(x \notin {{\,\mathrm{dom}\,}}\,h\) ). By \({\mathrm{arg~min}}_{{\mathbb {R}}^{n}} h\) we mean the set of all minimizers of h .

A function h with a convex domain is said to be

convex if, given any \(x, y \in {{\,\mathrm{dom}\,}}\,h\) , then

quasiconvex if, given any \(x, y \in {{\,\mathrm{dom}\,}}\,h\) , then

Every convex function is quasiconvex. The function \(h: {\mathbb {R}} \rightarrow {\mathbb {R}}\) with \(h(x) = x^{3}\) is quasiconvex without being convex. Recall that

where \({{{\,\mathrm{epi}\,}}}\,h := \{(x,t) \in {\mathbb {R}}^{n} \times {\mathbb {R}}: h(x) \le t\}\) is the epigraph of h and \(S_{\lambda } (h) := \{x \in {\mathbb {R}}^{n}: h(x) \le \lambda \}\) its sublevel set at the height \(\lambda \in {\mathbb {R}}\) .

The proximity operator of parameter \(\gamma >0\) of a function \(h: {\mathbb {R}}^{n} \rightarrow \overline{{\mathbb {R}}}\) at \(x \in {\mathbb {R}}^{n}\) is defined by \({{{\,\mathrm{Prox}\,}}}_{{^\gamma }h}: {\mathbb {R}}^{n} \rightrightarrows {\mathbb {R}}^{n}\) with

Let K be a closed and convex set in \({\mathbb {R}}^n\) , \(h: K \rightarrow \overline{{\mathbb {R}}}\) with \(K \cap {{\,\mathrm{dom}\,}}h \ne \emptyset \) a proper function, and \(f: K \times K \rightarrow {\mathbb {R}}\) be a real-valued bifunction. We say that f is

monotone on K , if for every \(x, y \in K\)

h -pseudomonotone on K , if for every \(x, y \in K\)

Every monotone bifunction is h -pseudomonotone, but the converse statement is not true in general. Furthermore, if \(h \equiv 0\) , then 0-pseudomonotonicity coincides with the usual pseudomonotonicity, see [ 16 ].

A new class of generalized convex functions which includes some classes of quasiconvex functions and weakly convex functions along other functions was introduced in [ 13 ].

Definition 2.1

Let K be a closed set in \({\mathbb {R}}^{n}\) and \(h: {\mathbb {R}}^{n} \rightarrow \overline{{\mathbb {R}}}\) be a proper function such that \(K \cap {{\,\mathrm{dom}\,}}h \ne \emptyset \) . We say that h is prox-convex on K (with prox-convex value \(\alpha \) ) if there exists \(\alpha > 0\) such that for every \(z \in K\) , \({{\,\mathrm{Prox}\,}}_{h + \iota _{K}} (z) \ne \emptyset \) , and

Some basic properties of prox-convex functions are recalled below.

Let K be a closed set in \({\mathbb {R}}^{n}\) and \(h: {\mathbb {R}}^{n} \rightarrow \overline{{\mathbb {R}}}\) be a proper prox-convex function on K such that \(K \cap {{\,\mathrm{dom}\,}}\,h \ne \emptyset \) . Then the map \(z \rightarrow {{\,\mathrm{Prox}\,}}_{h+\iota _{K}} (z)\) is single-valued, i.e., the left-hand side of relation ( 2.8 ) holds as an equality (by a slight abuse of notation see [ 13 , Proposition 3.3]), and firmly nonexpansive on K , that is, given \(z_{1}, z_{2} \in K\) and \({\overline{x}}_{1} \in {{\,\mathrm{Prox}\,}}_{h + \iota _{K}} (z_{1})\) and \({\overline{x}}_{2} \in {{\,\mathrm{Prox}\,}}_{h + \iota _{K}} (z_{2})\) , one has

If h is a proper, lower semicontinuous and convex function, then h is prox-convex with prox-convex value \(\alpha =1\) (see [ 13 , Proposition 3.4]), but the converse statement does not hold in general. Indeed, the function \(h(x) = -x^{2}-x\) is prox-convex (with prox-convex value \(\alpha \) for every \(\alpha >0\) ) without being convex on \(K=[0, 1]\) . Furthermore, a class of quasiconvex functions which are prox-convex as well is analyzed in [ 13 , Section 3.2].

As was proved in [ 13 , Theorem 4.1], the classical proximal point algorithm remains convergent for optimization problems consisting in minimizing prox-convex functions, too.

In the literature one can find similar works where the proximity operator of a function is considered with respect to a given set like above, for instance [ 3 , 14 ] where the employed functions are not split from the corresponding sets either.

We are not aware of any universal recipe for computing the proximity operator of a prox-convex function with respect to a given set. The most direct approach (used also for the numerical experiments presented in Sect.  4 as well as in [ 13 ]) is to determine it by hand by means of basic calculus techniques for determining the minimum of a function over a set. Alternatively one could employ (or adapt if necessary) in order to computationally derive proximal points of functions over sets (as the algorithms actually use them at certain points and closed formulae of the corresponding proximity operators are not really necessary) the software packages from [ 40 ] (in julia ) or [ 26 ] (in python ). Related to this issue is the computation of proximal points of a convex function over a nonconvex set, a contribution to this direction being available in the recent work [ 15 ]. Note also that in [ 17 ] a method based on the computation of proximal points of piecewise affine models of certain classes of nonconvex functions is proposed for determining the proximal points of the latter, while in the convex case one finds a symbolic computation method in [ 25 ] and an interior one in [ 10 ], however the possible ways of extending them towards nonconvex frameworks or for functions restricted to sets require further investigations.

To the best of our knowledge besides the convex and prox-convex functions only the weakly convex ones have single-valued proximity operators (as noted in [ 17 ]). This feature is very relevant when constructing proximal point algorithms as the new iterate is uniquely determined and does not have to be picked from a set (that needs to be found and can also be empty).

For a further study on generalized convexity we refer to [ 4 , 16 ] among other works.

3 Nonconvex Mixed Variational Inequalities

Let \(K\subseteq {\mathbb {R}}^{n}\) be nonempty, \(T: {\mathbb {R}}^{n} \rightarrow {\mathbb {R}}^{n}\) be an operator and \(h: K \rightarrow {\mathbb {R}}\) a real-valued function. The mixed variational inequality problem or variational inequality of the second kind is defined by

We denote its solution set by S ( T ;  h ;  K ).

Following [ 23 , 31 ], problem ( 3.1 ) can be seen as a reformulation of a Walrasian equilibrium model or of an oligopolistic equilibrium model, where (after some transformations explained in [ 23 , Section 2]) the (monotone) operator T represents the demand, while h the supply. While in [ 23 ] the function representing the supply is taken convex (however no economical reason behind this choice is given), in [ 31 ] it is DC (difference of convex). Another concrete application that can be recast as a mixed variational inequality problem can be found in [ 12 ] (see also [ 11 ]), where electrical circuits involving devices like transistors are studied by means of mixed variational inequalities. There the involved (monotone) operator is linear, while the electrical superpotential of the practical diodes is represented by the involved function (taken convex in order to fit the theoretical model, again without any physical explanation). In [ 36 ] a dual variational formulation for strain of an elastoplasticity model with hardening is reformulated as a mixed variational inequality, while in [ 28 ] the same happens with the frictional contact of an elastic cylinder with a rigid obstacle, in the antiplane framework.

If \(h \equiv 0\) , ( 3.1 ) reduces to the variational inequality problem (see [ 8 , 9 , 22 ]). On the other hand, if \(T \equiv 0\) ( 3.1 ) reduces to the constrained optimization problem of minimizing h over K . When h is convex, ( 3.1 ) is a convex mixed variational inequality, for which one can find various (proximal point type) algorithms in the literature, for instance in [ 5 , 27 , 37 , 41 , 43 , 44 , 45 ]. However when involving nonconvex functions mixed variational inequalities become harder to approach. For instance, the solution sets of such problems may be empty even for a compact and convex set K as was noted in [ 30 , Example 3.1] (see also [ 20 , page 127]). Indeed, take \(T = I\) (the identity map), \(K = {\mathbb {B}} (0, 1)\) , and \(h: {\mathbb {R}}^{n} \rightarrow {\mathbb {R}}\) given by \(h(x) = - \Vert x \Vert ^{2}\) . Then ( 3.1 ) has no solutions. Assuming the existence of a solution to ( 3.1 ), denoted by \({\overline{x}} \in K\) , one has in ( 3.1 ) for \(y = -{\overline{x}}\)

Setting \({\overline{x}} = 0\) in ( 3.1 ), we have \(\langle 0, 0 \rangle + h(y) - h(0) = - \Vert y \Vert ^{2} \ge 0\) for all \(y \in K\) , a contradiction. Therefore, \(S(I; h; K) = \emptyset \) .

The reason behind this situation is the “conflict” between the properties of the operator T and those of the function h . Since we are searching for a point where an inequality is satisfied for all the considered variables, if h goes downwards (for instance, when it is concave), then T needs to go upwards faster and vice-versa. This conflict is restricted to nonconvex functions, since if h is convex ( 3.1 ) has a solution on any compact and convex set K . Existence results for the nonconvex and noncoercive setting can be found in [ 19 , 20 , 21 ], in which this conflict appears in a theoretical assumption called mixed variational inequality property (see [ 42 , Definition 3.1]).

For problem ( 3.1 ), let us consider the following additional assumptions

T is an L -Lipschitz-continuous operator on K , where \(L>0\) ;

h is a lower semicontinuous prox-convex function on K with prox-convex value \(\alpha > 0\) ;

T and h satisfy the following generalized monotonicity condition on K (cf. [ 27 , 39 ])

S ( T ;  h ;  K ) is nonempty.

If T is h -pseudomonotone on K (in particular, monotone), then T satisfies assumption ( A 3) (see [ 39 ]). Indeed, take \({\overline{x}} \in S(T; h; K)\) . Since T is h -pseudomonotone, we have for every \(y\in K\)

i.e., T satisfies assumption ( A 3).

Note also that the generalized monotonicity condition ( A 3) can be further weakened to [ 27 , Equation (71)] without losing the convergence of the algorithm proposed below.

Results guaranteeing existence of solutions to mixed variational inequalities beyond convexity may be found in [ 19 , 20 , 21 ].

The algorithm we consider for solving ( 3.1 ) was recently introduced by Malitsky in [ 27 ] with the involved function taken convex.

As a first result, we validate the stopping criterion of Algorithm 1 in our generalized convex framework. In the following statements the sequences \(\{x^k\}_k\) and \(\{z^k\}_k\) are the ones generated by Algorithm 1.

Proposition 3.1

If ( A 2) holds and \(x^{k+1} = x^{k} = z^{k}\) for some \(k\in {\mathbb {N}}\) , then the stopping point of Algorithm  1 is a solution of ( 3.1 ), i.e. \(x^{k} \in S(T; h; K)\) .

If \(x^{k+1} = x^{k} = z^{k}\) , then \(x^{k} = {{\,\mathrm{Prox}\,}}_{h + \iota _{K}} \left( x^{k} - (1/\alpha ) T(x^{k})\right) \) , so by ( 2.8 ), we have

i.e., \(x^{k} \in S(T; h; K)\) . \(\square \)

In order to state the convergence of Algorithm 1, we first show the following general result, whose proof follows the steps of the one of [ 27 , Theorem 1].

Suppose that assumptions ( Ai ) with \(i \in \{1,\ldots , 4\}\) hold. Let \(x^{1}, z^{0} \in K\) be arbitrary. Then for each \({\overline{x}} \in S(T; h; K)\) , the sequences \(\{x_{k}\}_k\) and \(\{z^{k}\}_k\) satisfy that

By applying relation ( 2.8 ) to Eq. 3.4 for \(k+1\) and k , we have

Take \(x = {\overline{x}} \in S(T; h; K)\) in the first equation, \(x=x^{k+1}\) in the second equation, and note that \(x^{k} - z^{k-1} = \phi (x^{k} - z^{k})\) . Thus,

By adding these inequalities, and since \({\overline{x}} - x^{k+1} = {\overline{x}} - x^{k} + x^{k} - x^{k+1}\) and \(\alpha > 0\) , we have

Since T satisfies assumption ( A 3), we have

i.e., it follows from ( 3.8 ) that

By applying ( 2.1 ), we have

From step (3.3), we have \(x^{k+1} = (1 + \phi ) z^{k+1} - \phi z^{k}\) , thus

By replacing ( 3.10 ) in Eq. ( 3.9 ), and since \(\phi ^{2} = 1 + \phi \) , \((\phi - 1) \Vert x^{k+1} - z^{k} \Vert ^{2} - \frac{1}{\phi } \Vert x^{k+1} - z^{k} \Vert ^{2} = 0\) , we have

Finally, since T is L -Lipschitz-continuous, it follows that

and the result follows by replacing this in Eq. ( 3.11 ). \(\square \)

As a consequence, we have the following statement.

Corollary 3.1

Suppose that assumptions ( Ai ) with \(i \in \{1,\ldots , 4\}\) hold. Let \(x^{1}, z^{0} \in K\) be arbitrary and \({\overline{x}} \in S(T; h; K)\) . If

then the sequences \(\{x^{k}\}_{k}\) and \(\{z^{k}\}_{k}\) satisfy that

Note that, in particular, if h is convex, then \(\alpha = 1\) . Hence, if \(L \le {\phi }/{2}\) , then relation ( 3.13 ) holds, which is the usual assumption for the convex case. Moreover, due to the convexity of h , we have \(\langle {\overline{x}} - z, x - {\overline{x}} \rangle \ge 0\) . Hence, \({\overline{x}} = {{\,\mathrm{Prox}\,}}_{h + \iota _{K}} (z)\) implies that

Then there exists \(\gamma \ge 1\) large enough such that condition ( 3.12 ) holds.

Now, we present the following convergence result of Algorithm 1.

Theorem 3.1

Suppose that assumptions ( Ai ) with \(i \in \{1,\ldots , 4\}\) hold. Let \(x^{1}, z^{0} \in K\) be arbitrary. If condition ( 3.12 ) holds, then the sequences \(\{x^{k}\}_k\) and \(\{z^{k}\}_k\) converge to a solution of problem ( 3.1 ).

Take an arbitrary \({\overline{x}} \in S(T; h; K)\) . It follows from Lemma  3.1 that the sequence \(\left\{ (1 + \phi ) \Vert z^{k+1} - {\overline{x}} \Vert ^{2} + \frac{\phi }{2} \Vert x^{k+1} - x^{k} \Vert ^{2} \right\} _k\) is bounded. Then, \(\{ \Vert z^{k} - {\overline{x}} \Vert \}_k\) and \(\{z^{k}\}_k\) are bounded too. Furthermore, by ( 3.5 ),

hence \(\{x^{k}\}_k\) has at least a cluster point. Going to subsequences if necessary, the same happens with \(\{z^{k}\}_k\) , too. By using (3.3), we have

Therefore, it follows by Eqs. ( 3.14 ) and ( 3.15 ) that \(\Vert x^{k+1} - x^{k} \Vert \rightarrow 0\) when \(k\rightarrow +\infty \) .

Now, take \({\widehat{x}}\) be an arbitrary cluster point of the sequence \(\{x^{k}\}_k\) generated by our algorithm, and recall Eq. ( 3.6 ):

Since h is lower semicontinuous and T is L -Lipschitz-continuous, by taking the limit in Eq. ( 3.6 ) (passing to subsequences if needed) and by using Eq. ( 3.15 ), we have

i.e., \({\widehat{x}} \in S(T; h; K)\) . Therefore, every cluster point of \(\{x^{k}\}_k\) is a solution of problem ( 3.1 ). \(\square \)

As explained before, the conflict between the properties of the function and those of the operator in the nonconvex case (something similar happens in Multiobjective Optimization where one has several conflicting objective functions) is controlled in Algorithm 1 in condition ( 3.12 ). However, note that if \(T=0\) , then \(L=0\) and ( 3.12 ) holds automatically. On the other hand, if h is convex (in particular \(\iota _{K}\) ), then \(\alpha = 1\) , so condition ( 3.12 ) becomes “ \(L \in \, ]0, {\phi }/{2}]\) ”, which is usual for the convex case. Note also that one can find in the literature various methods for determining the Lipschitz constants of the involved operators, see for instance [ 38 ].

In contrast to the methods proposed in [ 27 , 37 , 43 ] and references therein, Algorithm 1 is not restricted to the convexity of the function h . Other recent algorithms for solving mixed variational inequalities where the involved function is convex can be found also in [ 5 , 41 , 44 , 45 ].

If \(h \equiv 0\) , then Algorithm 1 is a variant of [ 39 , Algorithm 2.1] for operators T which satisfy the general monotonicity assumption ( A 4) with \(h \equiv 0\) .

Combining some steps in the proof of Theorem  3.1 (in particular Lemma  3.1 and ( 3.14 )), one can conclude that for any solution \({\overline{x}} \in S(T; h; K)\) the sequences \(\{x^{k} - {\overline{x}}\}_k\) and \(\{z^{k} - {\overline{x}}\}_k\) are convergent.

A legitimate question concerns the possible modification of the algorithm considered in this section by employing (constant or variable) stepsizes in the proximal (backward) steps. This can be done when the function \(\lambda \alpha h\) is prox-convex with prox-convex value \(\alpha >0\) (where \(\lambda \in \, ]0, \phi / (2L)]\) ) by replacing 3.4 with

The convergence statement of this modified algorithm is similar to Theorem  3.1 , its proof following analogously. However, when assuming h to be prox-convex with prox-convex value \(\alpha >0\) it is not known whether \(\lambda h\) (for some \(\lambda >0\) ) is prox-convex or not. While ( 2.8 ) implies a similar inequality for \(\lambda h\) with the prox-convex value \(\lambda \alpha \) , it is not sure that \({{\,\mathrm{Prox}\,}}_{h + \iota _{K}} (z) \ne \emptyset \) yields \({{\,\mathrm{Prox}\,}}_{\lambda h + \iota _{K}} (z) \ne \emptyset \) .

4 Numerical Experiments

We implemented the modification of Algorithm 1 presented in Remark  3.6 in matlab 2019b-Win64 on a Lenovo Yoga 260 Laptop with Windows 10 and an Intel Core i7 6500U CPU with 2.59 GHz and 16GB RAM. As stopping criterion of the algorithm we considered the situation when the absolute values of both the differences between \(x^{k+1}\) and \(x^k\) , and \(x^{k+1}\) and \(z^k\) are not larger than the considered error \(\varepsilon >0\) . First we considered a toy example, where one can already note the “conflict” between the properties of the involved operator and function, then an application in oligopolistic markets.

4.1 Theoretical Example

We consider first the following mixed variational inequality

that is a special case of ( 3.1 ) for \(K=[0, 1] \subseteq {\mathbb {R}}\) , \(h:{\mathbb {R}}\rightarrow {\mathbb {R}}\) , \(h(y)= - y^2-y\) , and \(T: {\mathbb {R}}\rightarrow {\mathbb {R}}\) , \(Tx=x\) . The function \(g: {\mathbb {R}}\rightarrow {\mathbb {R}}\) given by \(g(y) = \langle T(x), y\rangle + h(y)\) is prox-convex on K for any \(x\in K\) for any \(\alpha > 0\) and problem ( 4.1 ) has a unique solution \({\overline{x}}=1\in K\) . The fact that \(y \mapsto \langle T(x), y \rangle \) is increasing on K while h is decreasing on K adds additional complications to problem ( 4.1 ).

The value of the proximity operator of parameter \(\alpha \lambda \) of h (for fixed \(\alpha , \lambda >0\) ) over K at \(z-\lambda T(x)\in K\) , for \(x, z\in K\) , is, for the situations considered below, where \(\alpha \lambda <1/2\) , equal to \((z+\lambda (\alpha -x))/(1-2\lambda \alpha )\) when this lies in K , otherwise being 0 when \(\lambda (x-\alpha ) \ge z\) and 1 otherwise, i.e. when \(z + 3 \alpha \lambda - \lambda x >1\) . In case \(\alpha \lambda \ge 1/2\) the analysis can be done in a similar manner. Hence, as \(\lambda \alpha h\) is prox-convex, we can employ for solving ( 4.1 ) the modification of Algorithm 1 mentioned in Remark  3.6 with constant stepsize \(\lambda \alpha \) .

In Tables  1 and 2 we present the computational results obtained by implementing this algorithm for various choices of the involved parameters and of the allowed error \(\varepsilon > 0\) . In all the situations presented below we give the number of iterations needed by the program to reach the solution \({\overline{x}}=1\) of ( 4.1 ).

4.2 Application in Oligopolistic Equilibrium

The Nash-Cournot oligopolistic market equilibrium is a fundamental model in economics (see [ 23 , 31 ] for more on this and related references). It assumes that there are n companies producing a common homogeneous commodity. For \(i\in \{1, \ldots , n\}\) , company i has a strategy set \(D_i \subseteq {\mathbb {R}}_+\) , a cost function \(\varphi _i\) defined on the strategy set \(D = \prod _{i=1}^{n} D_i\) of the model and a profit function \(f_i\) that is usually defined as price times production minus costs (of producing the considered production). Each company is interested in maximizing its profit by choosing the corresponding production level under knowledge on demand of the market and of production of the competition (seen as input parameters). A commonly used solution notion in this model is the celebrated Nash equilibrium . A point (strategy) \({{\bar{x}}} = ({{\bar{x}}}_1, \ldots , {{\bar{x}}}_n)^\top \in D\) is said to be a Nash equilibrium point of this Nash-Cournot oligopolistic market model if

where the vector \({{\bar{x}}}[x_i]\) is obtained from \({{\bar{x}}}\) by replacing \({{\bar{x}}}_i\) with \(x_i\) . Following some transformations described in detail in [ 23 , 31 ], the problem of determining a Nash equilibrium of a Nash-Cournot oligopolistic market situation can be rewritten as a mixed variational inequality of type ( 3.1 ), where the involved operator captures various parameters and additional information and the function h is the sum of the cost functions of the considered companies, each of them depending on a different variable that represents the corresponding production.

Following the oligopolistic equilibrium model analyzed in [ 31 ], where some of the involved cost functions are convex and some DC, we consider the mixed variational inequality corresponding to a model with 5 companies, whose cost functions are defined as follows

The cost functions \(\varphi _1\) , \(\varphi _3\) and \(\varphi _5\) are prox-convex (see [ 13 ]), while \(\varphi _2\) and \(\varphi _4\) convex. Functions \(\varphi _1\) and \(\varphi _3\) were employed in the similar application considered in [ 31 ] (following the more applied paper [ 2 ]) as (DC) cost functions for oligopolistic equilibrium problems, while \(\varphi _4\) is the Huber loss function (cf. [ 18 ]) that is used in various contexts in economics and machine learning for quantifying costs. This model also includes functions with negative values such as \(\varphi _1\) that quantify the possibility of having negative costs, for instance in case of a surplus of energy on the market (as discussed in the recent works [ 1 , 7 ]). To make the problem more challenging from a mathematical point of view we consider the involved convex cost functions defined over the whole space. Unlike ( 4.1 ), the present problem is unbounded in the second and fourth argument (note that the corresponding constraint sets are not compact). Note moreover that different to the literature on algorithms for DC optimization problems where usually only critical points are determinable (and not optimal solutions), for the DC functions that are also prox-convex proximal point methods are capable of delivering global minima (on the considered sets).

In our numerical experiments for solving ( 3.1 ) (denoted ( OMP ) in this case) where \(T(x) = Ax\) , \(x\in {\mathbb {R}}^5\) , with \(A\in {\mathbb {R}}^{5\times 5}\) a real symmetric positive semidefinite matrix of norm 1 (for simplicity) and \(h(x_1, \ldots , x_5) = \sum _{i=1}^{5}\varphi _i(x_i)\) , we employed the modification of Algorithm 1 mentioned in Remark  3.6 with constant stepsize \(\lambda \alpha \) , for fixed \(\alpha , \lambda >0\) . In each experiment the matrix A is randomly generated and scaled in order to have \(L=1\) . The proximity operator of (the separable function) h has as components the ones of the involved functions, which are known (cf. [ 6 , 13 , 29 ]). For instance, the proximity operator of parameter \(\gamma >0\) of \(\varphi _1\) over [0, 2] at \(z\in [0, 2]\) , is, when \(\gamma < 1/2\) , equal to \((z+\gamma )/(1-2\gamma )\) when this lies in [0, 2], otherwise being 0 when \(z < -\gamma \) and 2 otherwise, while in case \(\gamma \ge 1/2\) the analysis can be done in a similar manner. In the following numerical implementations we apply these formulae for \(\gamma = \alpha \lambda < 1/2\) .

In Tables  3 and 4 we present the computational results obtained by implementing the mentioned algorithm in matlab for various choices of the involved parameters and of the allowed error \(\varepsilon > 0\) . In all the situations presented below we give the number of iterations and the CPU time needed by the program to reach a suitable approximation of the solution of the corresponding oligopolistic equilibrium problem. As one can notice, unlike in the experiments for solving ( 4.1 ) where the choice of \(\lambda \) and \(\alpha \) does not influence the number of iterations in a significant manner, in the present case this (like the CPU time) depends on the values of the two mentioned parameters.

5 Conclusions

We contribute to the study of mixed variational inequalities beyond convexity by showing that a recent proximal point type algorithm due to Malitsky remains convergent for a class of nonconvex mixed variational inequalities, too. The convergence statement holds when there is a certain relation between the Lipschitz constant of the governing operator of the mixed variational inequality and the prox-convex value of the involved function, which can be seen as a way to control the “conflict” between the properties of the mentioned operator and function. This conflict belongs to the nature of nonconvex mixed variational inequality problems since it is no longer present when the operator vanishes, and collapses to a standard assumption when the function is convex. Since this is the first (as far as we know) proximal point type algorithm for iteratively determining a solution to a generalized convex mixed variational inequality, this relation has not been analyzed in the literature yet.

In a subsequent work, we plan to continue with the study of nonconvex mixed variational inequalities and, in particular, to provide a deeper analysis of the mentioned relation and to extend beyond convexity other recent algorithms for solving convex mixed variational inequalities as well as methods of proximal point type for minimizing quasiconvex functions towards nonconvex mixed variational inequalities.

Data availability

The datasets generated during and/or analysed during the current study are available from the corresponding author on reasonable request.

Aust, B., Horsch, A.: Negative market prices on power exchanges: evidence and policy implications from Germany. Electr. J. 33 , article number: 106716 (2020)

Bigi, G., Passacantando, M.: Differentiated oligopolistic markets with concave cost functions via Ky Fan inequalities. Decis. Econ. Finance 40 , 63–79 (2017)

Article   MathSciNet   Google Scholar  

Boţ, R.I., Csetnek, E.R.: Proximal-gradient algorithms for fractional programming. Optimization 66 , 1383–1396 (2017)

Cambini, A., Martein, L.: Generalized Convexity and Optimization. Springer, Berlin (2009)

MATH   Google Scholar  

Chen, C., Ma, S., Yang, J.: A general inertial proximal point algorithm for mixed variational inequality problem. SIAM J. Optim. 25 , 2120–2142 (2015)

Combettes, P.L., Pesquet, J.-C.: Proximal thresholding algorithm for minimization over orthonormal bases. SIAM J. Optim. 18 , 1351–1376 (2007)

Corbet, S., Goodell, J.W., Günay, S.: Co-movements and spillovers of oil and renewable firms under extreme conditions: new evidence from negative WTI prices during COVID-19. Energy Econ. 92 , article number: 104978 (2020)

Facchinei, F., Pang, J.-S.: Finite-Dimensional Variational Inequalities and Complementarity Problems, vol. I. Springer, New York (2003)

Facchinei, F., Pang, J.-S.: Finite-Dimensional Variational Inequalities and Complementarity Problems, vol. II. Springer, New York (2003)

Friedlander, M.P., Goh, G.: Efficient evaluation of scaled proximal operators. arXiv:1603.05719 (2016)

Goeleven, D.: Complementarity and Variational Inequalities in Electronics. Academic Press, London (2017)

Goeleven, D.: Existence and uniqueness for a linear mixed variational inequality arising in electrical circuits with transistors. J. Optim. Theory Appl. 138 , 397–406 (2008)

Grad, S.-M., Lara, F.: An extension of proximal point algorithms beyond convexity . arXiv:2104.08822 (2021)

Gribonval, R., Nikolova, M.: A characterization of proximity operators. J. Math. Imaging Vis. 62 , 773–789 (2020)

Gupta, S.D., Stellato, B., Van Parys, B.P.G.: Exterior-point operator splitting for nonconvex learning. arXiv:2011.04552 (2020)

Hadjisavvas, N., Komlosi, S., Schaible, S.: Handbook of Generalized Convexity and Generalized Monotonicity. Springer, Boston (2005)

Book   Google Scholar  

Hare, W., Sagastizábal, C.: Computing proximal points of nonconvex functions. Math. Program. 116 , 221–258 (2009)

Huber, P.J.: Robust estimation of a location parameter. Ann. Math. Stat. 35 , 73–101 (1964)

Iusem, A., Lara, F.: Optimality conditions for vector equilibrium problems with applications. J. Optim. Theory Appl. 180 , 187–206 (2019)

Iusem, A., Lara, F.: Existence results for noncoercive mixed variational inequalities in finite dimensional spaces. J. Optim. Theory Appl. 183 , 122–138 (2019)

Iusem, A., Lara, F.: A note on “Existence results for noncoercive mixed variational inequalities in finite dimensional spaces”. J. Optim. Theory Appl. 187 , 607–608 (2020)

Kinderlehrer, D., Stampacchia, G.: An Introduction to Variational Inequalities and Their Applications. Academic Press, New York (1980)

Konnov, I., Volotskaya, E.O.: Mixed variational inequalities and economic equilibrium problems. J. Appl. Math. 6 , 289–314 (2002)

Langenberg, N., Tichatschke, R.: Interior proximal methods for quasiconvex optimization. J. Glob. Optim. 52 , 641–661 (2012)

Lauster, F., Luke, D.R., Tam, M.K.: Symbolic computation with monotone operators. Set Valued Var. Anal. 26 , 353–368 (2018)

Luke, D.R., Gretchko, S., Schulz, J., Jansen, M., Dornheim, A., Ziehe, S., Nahme, R., Tam, M.K., Mattson, P., Wilke, R., Hesse, R., Stalljahn, A.: ProxToolbox —a toolbox of algorithms and projection operators for implementing fixed point iterations based on the Prox operator. https://gitlab.gwdg.de/nam/ProxPython (2012)

Malitsky, Y.: Golden ratio algorithms for variational inequalities. Math. Program. 184 , 383–410 (2020)

Matei, A., Sofonea, M.: Solvability and optimization for a class of mixed variational problems. Optimization (2019). https://doi.org/10.1080/02331934.2019.1676242

Article   MATH   Google Scholar  

Moreau, J.-J.: Proximité et dualité dans un espace hilbertien. Bull. Soc. Math. Fr. 93 , 273–299 (1965)

Article   Google Scholar  

Muu, L.D., Nguyen, V.H., Quy, N.V.: On Nash–Cournot oligopolistic market equilibrium models with concave cost functions. J. Glob. Optim. 41 , 351–364 (2008)

Muu, L.D., Quy, N.V.: Global optimization from concave minimization to concave mixed variational inequality. Acta Math. Vietnam. 45 , 449–462 (2020)

Noor, M.A.: Proximal methods for mixed variational inequalities. J. Optim. Theory Appl. 115 , 447–452 (2002)

Noor, M.A., Huang, Z.: Some proximal methods for solving mixed variational inequalities. Appl. Anal. Article ID 610852 (2012)

Noor, M.A., Noor, K.I., Zainab, S., Al-Said, E.: Proximal algorithms for solving mixed bifunction variational inequalities. Int. J. Phys. Sci. 6 , 4203–4207 (2011)

Google Scholar  

Papa Quiroz, E.A., Mallma Ramirez, L., Oliveira, P.R.: An inexact proximal method for quasiconvex minimization. Eur. J. Oper. Res. 246 , 721–729 (2015)

Prigozhin, L.: Variational inequalities in critical-state problems. Physica D 197 , 197–210 (2004)

Quoc, T.D., Muu, L.D., Hien, N.V.: Extragradient algorithms extended to equilibrium problems. Optimization 57 , 749–766 (2008)

Scaman, K., Virmaux, A.: Lipschitz regularity of deep neural networks: analysis and efficient estimation. In: Proceedings of the 32nd Conference on Neural Information Processing Systems (NeurIPS 2018), Adv Neural Inform Process Syst, pp. 3835–3844 (2018)

Solodov, M., Svaiter, B.F.: A new projection method for variational inequality problems. SIAM J. Control. Optim. 37 , 765–776 (1999)

Stella, L., Antonello, N., Fält, M.: ProximalOperators.jl—proximal operators for nonsmooth optimization in Julia . https://github.com/kul-forbes/ProximalOperators.jl (2018)

Thakur, B.S., Varghese, S.: Approximate solvability of general strongly mixed variational inequalities. Tbil. Math. J. 6 , 13–20 (2013)

MathSciNet   MATH   Google Scholar  

Wang, M.: The existence results and Tikhonov regularization method for generalized mixed variational inequalities in Banach spaces. Ann. Math. Phys. 7 , 151–163 (2017)

Wang, Z., Chen, Z., Xiao, Y., Zhang, C.: A new projection-type method for solving multi-valued mixed variational inequalities without monotonicity. Appl. Anal. (2018). https://doi.org/10.1080/00036811.2018.1538499

Xia, F.-Q., Huang, N.-J.: An inexact hybrid projection-proximal point algorithm for solving generalized mixed variational inequalities. Comput. Math. Appl. 62 , 4596–4604 (2011)

Xia, F.-Q., Zou, Y.-Z.: A projective splitting algorithm for solving generalized mixed variational inequalities. J. Inequal. Appl 2011 , 27 (2011)

Download references

Acknowledgements

This research was partially supported by FWF (Austrian Science Fund), project M-2045 (S.-M. Grad) and Conicyt–Chile under project Fondecyt Iniciación 11180320 (F. Lara). The authors are grateful to the handling Associate Editor and two anonymous reviewers for comments and suggestions that contributed to improving the quality of the manuscript.

Open access funding provided by University of Vienna.

Author information

Authors and affiliations.

Faculty of Mathematics, University of Vienna, Oskar-Morgenstern-Platz 1, 1090, Vienna, Austria

Sorin-Mihai Grad

Departamento de Matemática, Facultad de Ciencias, Universidad de Tarapacá, Arica, Chile

Felipe Lara

You can also search for this author in PubMed   Google Scholar

Corresponding author

Correspondence to Sorin-Mihai Grad .

Additional information

Publisher's note.

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/ .

Reprints and permissions

About this article

Grad, SM., Lara, F. Solving Mixed Variational Inequalities Beyond Convexity. J Optim Theory Appl 190 , 565–580 (2021). https://doi.org/10.1007/s10957-021-01860-9

Download citation

Received : 24 February 2021

Accepted : 05 April 2021

Published : 26 June 2021

Issue Date : August 2021

DOI : https://doi.org/10.1007/s10957-021-01860-9

Share this article

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

• Variational inequalities
• Quasiconvex functions
• Proximal point algorithms
• Golden Ratio Algorithms
• Find a journal
• Publish with us
• Track your research

Module 8: Systems of Linear Equations

Mixture problems, learning outcomes.

• Solve mixture problems

Write a system of linear equations representing a mixture problem, solve the system and interpret the results

One application of systems of equations are mixture problems. Mixture problems are ones where two different solutions are mixed together resulting in a new final solution.  A solution is a mixture of two or more different substances like water and salt or vinegar and oil.  Most biochemical reactions occur in liquid solutions, making them important for doctors, nurses, and researchers to understand.  There are many other disciplines that use solutions as well.

The concentration or strength of a liquid solution is often described  as a percentage.  This number comes from the ratio of how much mass is in a specific volume of liquid.  For example if you have [latex]50[/latex] grams of salt in a [latex]100mL[/latex] of water you have a [latex]50\%[/latex] salt solution based on the following ratio:

[latex]\frac{50\text{ grams }}{100\text{ mL }}=0.50\frac{\text{ grams }}{\text{ mL }}=50\text{ % }[/latex]

Solutions used for most purposes typically come in pre-made concentrations from manufacturers, so if you need a custom concentration, you would need to mix two different strengths.  In this section, we will practice writing equations that represent the outcome from mixing two different concentrations of solutions.

We will use the following table to help us solve mixture problems:

To demonstrate why the table is helpful in solving for unknown amounts or concentrations of a solution, consider two solutions that are mixed together, one is [latex]120mL[/latex] of a [latex]9\%[/latex] solution, and the other is 75mL of a 23% solution. If we mix both of these solutions together we will have a new volume and a new mass of solute and with those we can find a new concentration.

First, find the total mass of solids for each solution by multiplying the volume by the concentration.

Next we add the new volumes and new masses.

Now we have used mathematical operations to describe the result of mixing two different solutions. We know the new volume, concentration and mass of solute in the new solution.  In the following examples, you will see that we can use the table to find an unknown final volume or concentration. These problems can have either one or two variables. We will start with one variable problems, then move to two variable problems.

A chemist has [latex]70 mL[/latex] of a [latex]50\%[/latex] methane solution. How much of an [latex]80\%[/latex] solution must she add so the final solution is [latex]60\%[/latex] methane?

Let’s use the problem solving process outlined previously to help us work through a solution to the problem.

Read and Understand:  We are looking for a new amount – in this case a volume –  based on the words “how much”.  We know two starting  concentrations and the final concentration, as well as one volume.

Define and Translate:  Solution 1 is the [latex]70 mL[/latex] of [latex]50\%[/latex] methane and solution 2 is the unknown amount with [latex]80\%[/latex] methane.  We can call our unknown amount [latex]x[/latex].

Write and Solve:   Set up the mixture table. Remember that concentrations are written as decimals before we can perform mathematical operations on them.

Multiply amount by concentration to get total, be sure to distribute on the last row: [latex]\left(70 + x\right)0.6[/latex]Add the entries in the amount column to get final amount. The concentration for this amount is [latex]0.6[/latex] because we want the final solution to be [latex]60\%[/latex] methane.

Add the total mass for solution 1 and solution 2 to get the total mass for the [latex]60\%[/latex] solution. This is our equation for finding the unknown volume.

[latex]35+0.8x=42+0.6x[/latex]

[latex]\begin{array}{c}35+0.8x=42+0.6x\\\underline{-0.6x}\,\,\,\,\,\,\,\underline{-0.6x}\\35+0.2x=42\\\end{array}[/latex]

Subtract [latex]35[/latex] from both sides

[latex]\begin{array}{c}35+0.2x=42\\\underline{-35}\,\,\,\,\,\,\,\underline{-35}\\0.2x=7\end{array}[/latex]

Divide both sides by [latex]0.2[/latex]

[latex]\begin{array}{c}0.2x=7\\\frac{0.2x}{0.2}=\frac{7}{0.2}\end{array}[/latex] [latex]x=35[/latex]

[latex]35mL[/latex] of the [latex]80\%[/latex] solution must be added to the original [latex]70mL[/latex] of the [latex]50\%[/latex] solution to gain a solution with a concentration of [latex]60\%[/latex].

The above problem illustrates how we can use the mixture table to define an equation to solve for an unknown volume. In the next example we will start with two known concentrations and use a system of equations to find two starting volumes necessary to achieve a specified final concentration.

A farmer has two types of milk, one that is [latex]24\%[/latex] butterfat and another which is [latex]18\%[/latex] butterfat. How much of each should he use to end up with [latex]42[/latex] gallons of [latex]20\%[/latex] butterfat?

Read and Understand:  We are asked to find two starting volumes of milk whose concentrations of butterfat are both known. We also know the final volume is [latex]42[/latex] gallons. There are two unknowns in this problem.

Define and Translate:  We will call the unknown volume of the  [latex]24\%[/latex] solution [latex]x[/latex], and the unknown volume of the [latex]18\%[/latex] solution [latex]y[/latex].

Write and Solve:  Fill in the table with the information we know.

Find the total mass by multiplying the amount of each solution by the concentration. The total mass of the final solution comes from

When you sum the amount column you get one equation: [latex]x+ y = 42[/latex] When you sum the total column you get a second equation: [latex]0.24x + 0.18y = 8.4[/latex]

Use elimination to find a value for [latex]x[/latex] and [latex]y[/latex].

Multiply the first equation by [latex]-0.18[/latex]

[latex]-0.18(x+y) = (42)(-0.18)[/latex]

[latex]-0.18x - 0.18y = -7.56[/latex]

Now our system of equations looks like this:

[latex]0.24x + 0.18y = 8.4[/latex]

Adding the two equations together to eliminate the y terms gives this equation:

[latex]0.06x = 8.4[/latex]

Divide by [latex]0.06[/latex] on each side:

[latex]x = 14[/latex]

Now substitute the value for [latex]x[/latex] into one of the equations in order to solve for [latex]y[/latex].

[latex](14) + y = 42[/latex]

[latex]y = 28[/latex]

This can be interpreted as [latex]14[/latex] gallons of [latex]24\%[/latex] butterfat milk added to [latex]28[/latex] gallons of [latex]18\%[/latex] butterfat milk will give [latex]42[/latex] gallons of [latex]20\%[/latex] butterfat milk.

In the following video you will be given an example of how to solve a mixture problem without using a table, and interpret the results.

Contribute!

Improve this page Learn More

• Revision and Adaptation. Provided by : Lumen Learning. License : CC BY: Attribution
• Ex: System of Equations Application - Mixture Problem. Authored by : James Sousa (Mathispower4u.com) for Lumen Learning. Located at : https://youtu.be/4s5MCqphpKo . License : CC BY: Attribution
• Unit 14: Systems of Equations and Inequalities, from Developmental Math: An Open Program. Provided by : Monterey Institute of Technology and Education. Located at : . License : CC BY: Attribution
• Beginning and Intermediate Algebra Textbook. Authored by : Tyler Wallace. Located at : http://www.wallace.ccfaculty.org/book/book.html . License : CC BY: Attribution
• College Algebra. Authored by : Abramson, Jay. Provided by : OpenStax. Located at : https://openstaxcollege.org/textbooks/college-algebra . License : CC BY: Attribution

• {{subColumn.name}}

AIMS Mathematics

• {{newsColumn.name}}
• Share facebook twitter google linkedin

Generalized viscosity approximation method for solving split generalized mixed equilibrium problem with application to compressed sensing

• Charu Batra 1 , 
• Renu Chugh 2 , 
• Mohammad Sajid 3 ,  ,  , 
• Nishu Gupta 4 , 
• Rajeev Kumar 1
• 1. Department of Mathematics, Maharshi Dayanand University, Rohtak 124001, India
• 2. Department of Mathematics, Gurugram University, Haryana 122413, India
• 3. Department of Mechanical Engineering, College of Engineering, Qassim University, Buraydah 51452, Saudi Arabia
• 4. Department of Mathematics, Government College, Julana, Jind 126101, India
• Received: 01 November 2023 Revised: 01 December 2023 Accepted: 05 December 2023 Published: 13 December 2023

MSC : 47H09, 47H10

• Full Text(HTML)
• Download PDF

In this study, we establish a new inertial generalized viscosity approximation method and prove that the resulting sequence strongly converges to a common solution of a split generalized mixed equilibrium problem, fixed point problem for a finite family of nonexpansive mappings and hierarchical fixed point problem in real Hilbert spaces. As an application, we demonstrate the use of our main finding in compressed sensing in signal processing. Additionally, we include numerical examples to evaluate the efficiency of the suggested method and then conduct a comparative analysis of its efficiency with different methods. Our findings can be used in a variety of contexts to improve results.

• projection operator ,
• hierarchical fixed point ,
• equilibrium problem ,
• CQ-algorithm ,
• approximation ,
• iterative methods ,
• numerical results

Citation: Charu Batra, Renu Chugh, Mohammad Sajid, Nishu Gupta, Rajeev Kumar. Generalized viscosity approximation method for solving split generalized mixed equilibrium problem with application to compressed sensing[J]. AIMS Mathematics, 2024, 9(1): 1718-1754. doi: 10.3934/math.2024084

Related Papers:

• This work is licensed under a Creative Commons Attribution-NonCommercial-Share Alike 4.0 Unported License. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-sa/4.0/ -->

Supplements

Access history.

• Corresponding author: Email: [email protected] ; 

Reader Comments

• © 2024 the Author(s), licensee AIMS Press. This is an open access article distributed under the terms of the Creative Commons Attribution License ( http://creativecommons.org/licenses/by/4.0 )

通讯作者: 陈斌, [email protected]

沈阳化工大学材料科学与工程学院 沈阳 110142

Article views( 498 ) PDF downloads( 43 ) Cited by( 0 )

Figures and Tables

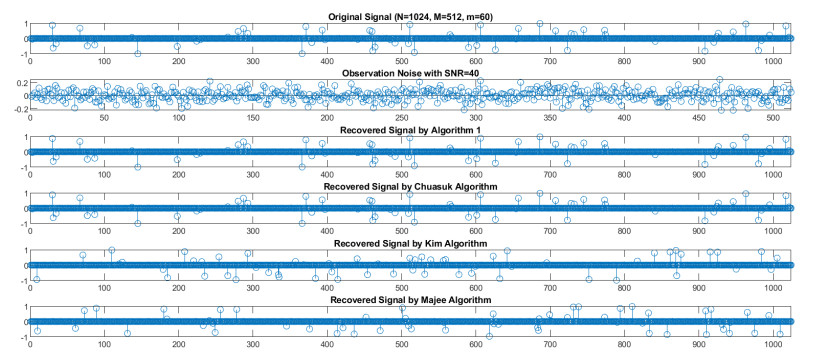
Figures( 4 )  /  Tables( 3 )

Associated material

Other articles by authors.

• Charu Batra
• Mohammad Sajid
• Nishu Gupta
• Rajeev Kumar

Related pages

• on Google Scholar
• Email to a friend
• Order reprints

Export File

• Figure 1. From top to bottom: original signal, observed value and recovered signals by Algorithm 3.1, the Chuasuk Algorithm [ 37 ] , the Kim Algorithm [ 26 ] and the Majee Algorithm [ 24 ]
• Figure 2. Numerical results for MSE versus the number of iterations (n) when $ N = 1024, $ $ M = 512, $ and $ m = 60 $
• Figure 3. Example 5.1: Comparison of Algorithm 3.1 with the Chuasuk Algorithm [ 37 ] , the Kim Algorithm [ 26 ] and the Majee Algorithm [ 24 ]
• Figure 4. Example 5.2: Algorithm comparison 3.1 with the Chuasuk Algorithm [ 37 ] , the Kim Algorithm [ 26 ] and the Majee Algorithm [ 24 ]

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons
• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

4.9: Strategies for Solving Applications and Equations

• Last updated
• Save as PDF
• Page ID 113697

Learning Objectives

By the end of this section, you will be able to:

• Use a problem solving strategy for word problems
• Solve number word problems
• Solve percent applications
• Solve simple interest applications

Before you get started, take this readiness quiz.

• Translate “six less than twice x ” into an algebraic expression. If you missed this problem, review [link] .
• Convert 4.5% to a decimal. If you missed this problem, review [link] .
• Convert 0.6 to a percent. If you missed this problem, review [link] .

Have you ever had any negative experiences in the past with word problems? When we feel we have no control, and continue repeating negative thoughts, we set up barriers to success. Realize that your negative experiences with word problems are in your past. To move forward you need to calm your fears and change your negative feelings.

Start with a fresh slate and begin to think positive thoughts. Repeating some of the following statements may be helpful to turn your thoughts positive. Thinking positive thoughts is a first step towards success.

• I think I can! I think I can!
• While word problems were hard in the past, I think I can try them now.
• I am better prepared now—I think I will begin to understand word problems.
• I am able to solve equations because I practiced many problems and I got help when I needed it—I can try that with word problems.
• It may take time, but I can begin to solve word problems.
• You are now well prepared and you are ready to succeed. If you take control and believe you can be successful, you will be able to master word problems.

Use a Problem Solving Strategy for Word Problems

Now that we can solve equations, we are ready to apply our new skills to word problems. We will develop a strategy we can use to solve any word problem successfully.

EXAMPLE \(\PageIndex{1}\)

Normal yearly snowfall at the local ski resort is 12 inches more than twice the amount it received last season. The normal yearly snowfall is 62 inches. What was the snowfall last season at the ski resort?

EXAMPLE \(\PageIndex{2}\)

Guillermo bought textbooks and notebooks at the bookstore. The number of textbooks was three more than twice the number of notebooks. He bought seven textbooks. How many notebooks did he buy?

He bought two notebooks

EXAMPLE \(\PageIndex{3}\)

Gerry worked Sudoku puzzles and crossword puzzles this week. The number of Sudoku puzzles he completed is eight more than twice the number of crossword puzzles. He completed 22 Sudoku puzzles. How many crossword puzzles did he do?

He did seven crosswords puzzles

We summarize an effective strategy for problem solving.

PROBLEM SOLVING STRATEGY FOR WORD PROBLEMS

• Read the problem. Make sure all the words and ideas are understood.
• Identify what you are looking for.
• Name what you are looking for. Choose a variable to represent that quantity.
• Translate into an equation. It may be helpful to restate the problem in one sentence with all the important information. Then, translate the English sentence into an algebra equation.
• Solve the equation using proper algebra techniques.
• Check the answer in the problem to make sure it makes sense.
• Answer the question with a complete sentence.

Solve Number Word Problems

We will now apply the problem solving strategy to “number word problems.” Number word problems give some clues about one or more numbers and we use these clues to write an equation. Number word problems provide good practice for using the Problem Solving Strategy.

EXAMPLE \(\PageIndex{4}\)

The sum of seven times a number and eight is thirty-six. Find the number.

Did you notice that we left out some of the steps as we solved this equation? If you’re not yet ready to leave out these steps, write down as many as you need.

EXAMPLE \(\PageIndex{5}\)

The sum of four times a number and two is fourteen. Find the number.

EXAMPLE \(\PageIndex{6}\)

The sum of three times a number and seven is twenty-five. Find the number.

Some number word problems ask us to find two or more numbers. It may be tempting to name them all with different variables, but so far, we have only solved equations with one variable. In order to avoid using more than one variable, we will define the numbers in terms of the same variable. Be sure to read the problem carefully to discover how all the numbers relate to each other.

EXAMPLE \(\PageIndex{7}\)

The sum of two numbers is negative fifteen. One number is nine less than the other. Find the numbers.

EXAMPLE \(\PageIndex{8}\)

The sum of two numbers is negative twenty-three. One number is seven less than the other. Find the numbers.

\(−15,−8\)

EXAMPLE \(\PageIndex{9}\)

The sum of two numbers is negative eighteen. One number is forty more than the other. Find the numbers.

\(−29,11\)

Consecutive Integers (optional)

Some number problems involve consecutive integers . Consecutive integers are integers that immediately follow each other. Examples of consecutive integers are:

\[\begin{array}{rrrr} 1, & 2, & 3, & 4 \\ −10, & −9, & −8, & −7\\ 150, & 151, & 152, & 153 \end{array}\]

Notice that each number is one more than the number preceding it. Therefore, if we define the first integer as n , the next consecutive integer is \(n+1\). The one after that is one more than \(n+1\), so it is \(n+1+1\), which is \(n+2\).

\[\begin{array}{ll} n & 1^{\text{st}} \text{integer} \\ n+1 \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; & 2^{\text{nd}}\text{consecutive integer} \\ n+2 & 3^{\text{rd}}\text{consecutive integer} \;\;\;\;\;\;\;\; \text{etc.} \end{array}\]

We will use this notation to represent consecutive integers in the next example.

EXAMPLE \(\PageIndex{10}\)

Find three consecutive integers whose sum is \(−54\).

EXAMPLE \(\PageIndex{11}\)

Find three consecutive integers whose sum is \(−96\).

\(−33,−32,−31\)

EXAMPLE \(\PageIndex{12}\)

Find three consecutive integers whose sum is \(−36\).

\(−13,−12,−11\)

Now that we have worked with consecutive integers, we will expand our work to include consecutive even integers and consecutive odd integers . Consecutive even integers are even integers that immediately follow one another. Examples of consecutive even integers are:

\[24, 26, 28\]

\[−12,−10,−8\]

Notice each integer is two more than the number preceding it. If we call the first one n , then the next one is \(n+2\). The one after that would be \(n+2+2\) or \(n+4\).

Consecutive odd integers are odd integers that immediately follow one another. Consider the consecutive odd integers 63, 65, and 67.

\[63, 65, 67\]

\[n,n+2,n+4\]

Does it seem strange to have to add two (an even number) to get the next odd number? Do we get an odd number or an even number when we add 2 to 3? to 11? to 47?

Whether the problem asks for consecutive even numbers or odd numbers, you do not have to do anything different. The pattern is still the same—to get to the next odd or the next even integer, add two.

EXAMPLE \(\PageIndex{13}\)

Find three consecutive even integers whose sum is \(120\).

EXAMPLE \(\PageIndex{14}\)

Find three consecutive even integers whose sum is 102.

\(32, 34, 36\)

EXAMPLE \(\PageIndex{15}\)

Find three consecutive even integers whose sum is \(−24\).

\(−10,−8,−6\)

When a number problem is in a real life context, we still use the same strategies that we used for the previous examples.

EXAMPLE \(\PageIndex{16}\)

A married couple together earns $110,000 a year. The wife earns $16,000 less than twice what her husband earns. What does the husband earn?

According to the National Automobile Dealers Association, the average cost of a car in 2014 was $28,400. This was $1,600 less than six times the cost in 1975. What was the average cost of a car in 1975?

The average cost was $5,000.

EXAMPLE \(\PageIndex{18}\)

US Census data shows that the median price of new home in the U.S. in November 2014 was $280,900. This was $10,700 more than 14 times the price in November 1964. What was the median price of a new home in November 1964?

The median price was $19,300.

Solve Percent Applications

There are several methods to solve percent equations. In algebra, it is easiest if we just translate English sentences into algebraic equations and then solve the equations. Be sure to change the given percent to a decimal before you use it in the equation.

EXAMPLE \(\PageIndex{19}\)

Translate and solve:

• What number is 45% of 84?
• 8.5% of what amount is $4.76?
• 168 is what percent of 112?
• What number is 45% of 80?
• 7.5% of what amount is $1.95?
• 110 is what percent of 88?

ⓐ 36 ⓑ $26 ⓒ \(125 \% \)

EXAMPLE \(\PageIndex{21}\)

• What number is 55% of 60?
• 8.5% of what amount is $3.06?
• 126 is what percent of 72?

ⓐ 33 ⓑ $36 ⓐ \(175 \% \)

Now that we have a problem solving strategy to refer to, and have practiced solving basic percent equations, we are ready to solve percent applications. Be sure to ask yourself if your final answer makes sense—since many of the applications we will solve involve everyday situations, you can rely on your own experience.

EXAMPLE \(\PageIndex{22}\)

The label on Audrey’s yogurt said that one serving provided 12 grams of protein, which is 24% of the recommended daily amount. What is the total recommended daily amount of protein?

EXAMPLE \(\PageIndex{23}\)

One serving of wheat square cereal has 7 grams of fiber, which is 28% of the recommended daily amount. What is the total recommended daily amount of fiber?

EXAMPLE \(\PageIndex{24}\)

One serving of rice cereal has 190 mg of sodium, which is 8% of the recommended daily amount. What is the total recommended daily amount of sodium?

Remember to put the answer in the form requested. In the next example we are looking for the percent.

EXAMPLE \(\PageIndex{25}\)

Veronica is planning to make muffins from a mix. The package says each muffin will be 240 calories and 60 calories will be from fat. What percent of the total calories is from fat?

EXAMPLE \(\PageIndex{26}\)

Mitzi received some gourmet brownies as a gift. The wrapper said each 28% brownie was 480 calories, and had 240 calories of fat. What percent of the total calories in each brownie comes from fat? Round the answer to the nearest whole percent.

EXAMPLE \(\PageIndex{27}\)

The mix Ricardo plans to use to make brownies says that each brownie will be 190 calories, and 76 calories are from fat. What percent of the total calories are from fat? Round the answer to the nearest whole percent.

It is often important in many fields—business, sciences, pop culture—to talk about how much an amount has increased or decreased over a certain period of time. This increase or decrease is generally expressed as a percent and called the percent change .

To find the percent change, first we find the amount of change, by finding the difference of the new amount and the original amount. Then we find what percent the amount of change is of the original amount.

FIND PERCENT CHANGE

\[\text{change}= \text{new amount}−\text{original amount}\]

change is what percent of the original amount?

EXAMPLE \(\PageIndex{28}\)

Recently, the California governor proposed raising community college fees from $36 a unit to $46 a unit. Find the percent change. (Round to the nearest tenth of a percent.)

EXAMPLE \(\PageIndex{29}\)

Find the percent change. (Round to the nearest tenth of a percent.) In 2011, the IRS increased the deductible mileage cost to 55.5 cents from 51 cents.

\(8.8 \% \)

EXAMPLE \(\PageIndex{30}\)

Find the percent change. (Round to the nearest tenth of a percent.) In 1995, the standard bus fare in Chicago was $1.50. In 2008, the standard bus fare was 2.25.

Applications of discount and mark-up are very common in retail settings.

When you buy an item on sale, the original price has been discounted by some dollar amount. The discount rate , usually given as a percent, is used to determine the amount of the discount . To determine the amount of discount, we multiply the discount rate by the original price.

The price a retailer pays for an item is called the original cost . The retailer then adds a mark-up to the original cost to get the list price , the price he sells the item for. The mark-up is usually calculated as a percent of the original cost. To determine the amount of mark-up, multiply the mark-up rate by the original cost.

\[ \begin{align} \text{amount of discount} &= \text{discount rate}· \text{original price} \\ \text{sale price} &= \text{original amount}– \text{discount price} \end{align}\]

The sale price should always be less than the original price.

\[\begin{align} \text{amount of mark-up} &= \text{mark-up rate}·\text{original price} \\ \text{list price} &= \text{original cost}–\text{mark-up} \end{align}\]

The list price should always be more than the original cost.

EXAMPLE \(\PageIndex{31}\)

Liam’s art gallery bought a painting at an original cost of $750. Liam marked the price up 40%. Find

• the amount of mark-up and
• the list price of the painting.

EXAMPLE \(\PageIndex{32}\)

Find ⓐ the amount of mark-up and ⓑ the list price: Jim’s music store bought a guitar at original cost $1,200. Jim marked the price up 50%.

ⓐ $600 ⓑ $1,800

EXAMPLE \(\PageIndex{33}\)

Find ⓐ the amount of mark-up and ⓑ the list price: The Auto Resale Store bought Pablo’s Toyota for $8,500. They marked the price up 35%.

ⓐ $2,975 ⓑ $11,475

Solve Simple Interest Applications

Interest is a part of our daily lives. From the interest earned on our savings to the interest we pay on a car loan or credit card debt, we all have some experience with interest in our lives.

The amount of money you initially deposit into a bank is called the principal , P , and the bank pays you interest, I. When you take out a loan, you pay interest on the amount you borrow, also called the principal.

In either case, the interest is computed as a certain percent of the principal, called the rate of interest , r . The rate of interest is usually expressed as a percent per year, and is calculated by using the decimal equivalent of the percent. The variable t , (for time) represents the number of years the money is saved or borrowed.

Interest is calculated as simple interest or compound interest. Here we will use simple interest.

SIMPLE INTEREST

If an amount of money, P , called the principal, is invested or borrowed for a period of t years at an annual interest rate r , the amount of interest, I , earned or paid is

\[ \begin{array}{ll} I=Prt \; \; \; \; \; \; \; \; \; \; \; \; \text{where} & { \begin{align} I &= \text{interest} \\ P &= \text{principal} \\ r &= \text{rate} \\ t &= \text{time} \end{align}} \end{array}\]

Interest earned or paid according to this formula is called simple interest .

The formula we use to calculate interest is \(I=Prt\). To use the formula we substitute in the values for variables that are given, and then solve for the unknown variable. It may be helpful to organize the information in a chart.

EXAMPLE \(\PageIndex{34}\)

Areli invested a principal of $950 in her bank account that earned simple interest at an interest rate of 3%. How much interest did she earn in five years?

\( \begin{aligned} I & = \; ? \\ P & = \; \$ 950 \\ r & = \; 3 \% \\ t & = \; 5 \text{ years} \end{aligned}\)

\(\begin{array}{ll} \text{Identify what you are asked to find, and choose a} & \text{What is the simple interest?} \\ \text{variable to represent it.} & \text{Let } I= \text{interest.} \\ \text{Write the formula.} & I=Prt \\ \text{Substitute in the given information.} & I=(950)(0.03)(5) \\ \text{Simplify.} & I=142.5 \\ \text{Check.} \\ \text{Is } \$142.50 \text{ a reasonable amount of interest on } \$ \text{ 950?} \; \;\;\;\;\; \;\;\;\;\;\; \\ \text{Yes.} \\ \text{Write a complete sentence.} & \text{The interest is } \$ \text{142.50.} \end{array}\)

EXAMPLE \(\PageIndex{35}\)

Nathaly deposited $12,500 in her bank account where it will earn 4% simple interest. How much interest will Nathaly earn in five years?

He will earn $2,500.

EXAMPLE \(\PageIndex{36}\)

Susana invested a principal of $36,000 in her bank account that earned simple interest at an interest rate of 6.5%.6.5%. How much interest did she earn in three years?

She earned $7,020.

There may be times when we know the amount of interest earned on a given principal over a certain length of time, but we do not know the rate.

EXAMPLE \(\PageIndex{37}\)

Hang borrowed $7,500 from her parents to pay her tuition. In five years, she paid them $1,500 interest in addition to the $7,500 she borrowed. What was the rate of simple interest?

\( \begin{aligned} I & = \; \$ 1500 \\ P & = \; \$ 7500 \\ r & = \; ? \\ t & = \; 5 \text{ years} \end{aligned}\)

Identify what you are asked to find, and choose What is the rate of simple interest? a variable to represent it. Write the formula. Substitute in the given information. Multiply. Divide. Change to percent form. Let r = rate of interest. I = P r t 1,500 = ( 7,500 ) r ( 5 ) 1,500 = 37,500 r 0.04 = r 4 % = r Check. I = P r t 1,500 = ? ( 7,500 ) ( 0.04 ) ( 5 ) 1,500 = 1,500 ✓ Write a complete sentence. The rate of interest was 4%. Identify what you are asked to find, and choose What is the rate of simple interest? a variable to represent it. Write the formula. Substitute in the given information. Multiply. Divide. Change to percent form. Let r = rate of interest. I = P r t 1 ,500 = ( 7,500 ) r ( 5 ) 1,500 = 37,500 r 0.04 = r 4 % = r Check. I = P r t 1 ,500 = ? ( 7,500 ) ( 0.04 ) ( 5 ) 1,500 = 1, 500 ✓ Write a complete sentence. The rate of interest was 4%.

EXAMPLE \(\PageIndex{38}\)

Jim lent his sister $5,000 to help her buy a house. In three years, she paid him the $5,000, plus $900 interest. What was the rate of simple interest?

The rate of simple interest was 6%.

EXAMPLE \(\PageIndex{39}\)

Loren lent his brother $3,000 to help him buy a car. In four years, his brother paid him back the $3,000 plus $660 in interest. What was the rate of simple interest?

The rate of simple interest was 5.5%.

In the next example, we are asked to find the principal—the amount borrowed.

EXAMPLE \(\PageIndex{40}\)

Sean’s new car loan statement said he would pay $4,866,25 in interest from a simple interest rate of 8.5% over five years. How much did he borrow to buy his new car?

\( \begin{aligned} I & = \; 4,866.25 \\ P & = \; ? \\ r & = \; 8.5 \% \\ t & = \; 5 \text{ years} \end{aligned}\)

Identify what you are asked to find, What is the amount borrowed (the principal)? and choose a variable to represent it. Write the formula. Substitute in the given information. Multiply. Divide. Let P = principal borrowed. I = P r t 4,866.25 = P ( 0.085 ) ( 5 ) 4,866.25 = 0.425 P 11,450 = P Check. I = P r t 4,866.25 = ? ( 11,450 ) ( 0.085 ) ( 5 ) 4,866.25 = 4,866.25 ✓ Write a complete sentence. The principal was $11,450. Identify what you are asked to find, What is the amount borrowed (the principal)? and choose a variable to represent it. Write the formula. Substitute in the given information. Multiply. Divide. Let P = principal borrowed. I = P r t 4 ,866.25 = P ( 0.085 ) ( 5 ) 4,866.25 = 0.425 P 11,450 = P Check. I = P r t 4 ,866.25 = ? ( 11,450 ) ( 0.085 ) ( 5 ) 4,866.25 = 4,866.25 ✓ Write a complete sentence. The principal was $11,450.

EXAMPLE \(\PageIndex{41}\)

Eduardo noticed that his new car loan papers stated that with a 7.5% simple interest rate, he would pay $6,596.25 in interest over five years. How much did he borrow to pay for his car?

He paid $17,590.

EXAMPLE \(\PageIndex{42}\)

In five years, Gloria’s bank account earned $2,400 interest at 5% simple interest. How much had she deposited in the account?

She deposited $9,600.

Access this online resource for additional instruction and practice with using a problem solving strategy.

• Begining Arithmetic Problems

Key Concepts

\(\text{change}=\text{new amount}−\text{original amount}\)

\(\text{change is what percent of the original amount?}\)

• \( \begin{align} \text{amount of discount} &= \text{discount rate}· \text{original price} \\ \text{sale price} &= \text{original amount}– \text{discount price} \end{align}\)
• \(\begin{align} \text{amount of mark-up} &= \text{mark-up rate}·\text{original price} \\ \text{list price} &= \text{original cost}–\text{mark-up} \end{align}\)
• If an amount of money, P , called the principal, is invested or borrowed for a period of t years at an annual interest rate r , the amount of interest, I , earned or paid is: \[\begin{aligned} &{} &{} &{I=interest} \nonumber\\ &{I=Prt} &{\text{where} \space} &{P=principal} \nonumber\\ &{} &{\space} &{r=rate} \nonumber\\ &{} &{\space} &{t=time} \nonumber \end{aligned}\]

Practice Makes Perfect

1. List five positive thoughts you can say to yourself that will help you approach word problems with a positive attitude. You may want to copy them on a sheet of paper and put it in the front of your notebook, where you can read them often.

Answers will vary.

2. List five negative thoughts that you have said to yourself in the past that will hinder your progress on word problems. You may want to write each one on a small piece of paper and rip it up to symbolically destroy the negative thoughts.

In the following exercises, solve using the problem solving strategy for word problems. Remember to write a complete sentence to answer each question.

3. There are \(16\) girls in a school club. The number of girls is four more than twice the number of boys. Find the number of boys.

4. There are \(18\) Cub Scouts in Troop 645. The number of scouts is three more than five times the number of adult leaders. Find the number of adult leaders.

5. Huong is organizing paperback and hardback books for her club’s used book sale. The number of paperbacks is \(12\) less than three times the number of hardbacks. Huong had \(162\) paperbacks. How many hardback books were there?

58 hardback books

6. Jeff is lining up children’s and adult bicycles at the bike shop where he works. The number of children’s bicycles is nine less than three times the number of adult bicycles. There are \(42\) adult bicycles. How many children’s bicycles are there?

In the following exercises, solve each number word problem.

7. The difference of a number and \(12\) is three. Find the number.

8. The difference of a number and eight is four. Find the number.

9. The sum of three times a number and eight is \(23\). Find the number.

10. The sum of twice a number and six is \(14\). Find the number.

11 . The difference of twice a number and seven is \(17\). Find the number.

12. The difference of four times a number and seven is \(21\). Find the number.

13. Three times the sum of a number and nine is \(12\). Find the number.

14. Six times the sum of a number and eight is \(30\). Find the number.

15. One number is six more than the other. Their sum is \(42\). Find the numbers.

\(18, \;24\)

16. One number is five more than the other. Their sum is \(33\). Find the numbers.

17. The sum of two numbers is \(20\). One number is four less than the other. Find the numbers.

\(8, \;12\)

18 . The sum of two numbers is \(27\). One number is seven less than the other. Find the numbers.

19. One number is \(14\) less than another. If their sum is increased by seven, the result is \(85\). Find the numbers.

\(32,\; 46\)

20 . One number is \(11\) less than another. If their sum is increased by eight, the result is \(71\). Find the numbers.

21. The sum of two numbers is \(14\). One number is two less than three times the other. Find the numbers.

\(4,\; 10\)

22. The sum of two numbers is zero. One number is nine less than twice the other. Find the numbers.

23. The sum of two consecutive integers is \(77\). Find the integers.

\(38,\; 39\)

24. The sum of two consecutive integers is \(89\). Find the integers.

25. The sum of three consecutive integers is \(78\). Find the integers.

\(25,\; 26,\; 27\)

26. The sum of three consecutive integers is \(60\). Find the integers.

27. Find three consecutive integers whose sum is \(−36\).

\(−11,\;−12,\;−13\)

28. Find three consecutive integers whose sum is \(−3\).

29. Find three consecutive even integers whose sum is \(258\).

\(84,\; 86,\; 88\)

30. Find three consecutive even integers whose sum is \(222\).

31. Find three consecutive odd integers whose sum is \(−213\).

\(−69,\;−71,\;−73\)

32. Find three consecutive odd integers whose sum is \(−267\).

33. Philip pays \($1,620\) in rent every month. This amount is \($120\) more than twice what his brother Paul pays for rent. How much does Paul pay for rent?

34. Marc just bought an SUV for \($54,000\). This is \($7,400\) less than twice what his wife paid for her car last year. How much did his wife pay for her car?

35. Laurie has \($46,000\) invested in stocks and bonds. The amount invested in stocks is \($8,000\) less than three times the amount invested in bonds. How much does Laurie have invested in bonds?

\($13,500\)

36. Erica earned a total of \($50,450\) last year from her two jobs. The amount she earned from her job at the store was \($1,250\) more than three times the amount she earned from her job at the college. How much did she earn from her job at the college?

In the following exercises, translate and solve.

37. a. What number is 45% of 120? b. 81 is 75% of what number? c. What percent of 260 is 78?

a. 54 b. 108 c. 30%

38. a. What number is 65% of 100? b. 93 is 75% of what number? c. What percent of 215 is 86?

39. a. 250% of 65 is what number? b. 8.2% of what amount is $2.87? c. 30 is what percent of 20?

a. 162.5 b. $35 c. 150%

40. a. 150% of 90 is what number? b. 6.4% of what amount is $2.88? c. 50 is what percent of 40?

In the following exercises, solve.

41. Geneva treated her parents to dinner at their favorite restaurant. The bill was $74.25. Geneva wants to leave 16% of the total bill as a tip. How much should the tip be?

42. When Hiro and his co-workers had lunch at a restaurant near their work, the bill was $90.50. They want to leave 18% of the total bill as a tip. How much should the tip be?

43. One serving of oatmeal has 8 grams of fiber, which is 33% of the recommended daily amount. What is the total recommended daily amount of fiber?

44. One serving of trail mix has 67 grams of carbohydrates, which is 22% of the recommended daily amount. What is the total recommended daily amount of carbohydrates?

45. A bacon cheeseburger at a popular fast food restaurant contains 2070 milligrams (mg) of sodium, which is 86% of the recommended daily amount. What is the total recommended daily amount of sodium?

46. A grilled chicken salad at a popular fast food restaurant contains 650 milligrams (mg) of sodium, which is 27% of the recommended daily amount. What is the total recommended daily amount of sodium?

47. The nutrition fact sheet at a fast food restaurant says the fish sandwich has 380 calories, and 171 calories are from fat. What percent of the total calories is from fat?

48. The nutrition fact sheet at a fast food restaurant says a small portion of chicken nuggets has 190 calories, and 114 calories are from fat. What percent of the total calories is from fat?

49. Emma gets paid $3,000 per month. She pays $750 a month for rent. What percent of her monthly pay goes to rent?

50. Dimple gets paid $3,200 per month. She pays $960 a month for rent. What percent of her monthly pay goes to rent?

51. Tamanika received a raise in her hourly pay, from $15.50 to $17.36. Find the percent change.

52. Ayodele received a raise in her hourly pay, from $24.50 to $25.48. Find the percent change.

53. Annual student fees at the University of California rose from about $4,000 in 2000 to about $12,000 in 2010. Find the percent change.

54. The price of a share of one stock rose from $12.50 to $50. Find the percent change.

55. A grocery store reduced the price of a loaf of bread from $2.80 to $2.73. Find the percent change.

−2.5%

56. The price of a share of one stock fell from $8.75 to $8.54. Find the percent change.

57. Hernando’s salary was $49,500 last year. This year his salary was cut to $44,055. Find the percent change.

58. In ten years, the population of Detroit fell from 950,000 to about 712,500. Find the percent change.

In the following exercises, find a. the amount of discount and b. the sale price.

59. Janelle bought a beach chair on sale at 60% off. The original price was $44.95.

a. $26.97 b. $17.98

60. Errol bought a skateboard helmet on sale at 40% off. The original price was $49.95.

In the following exercises, find a. the amount of discount and b. the discount rate (Round to the nearest tenth of a percent if needed.)

61. Larry and Donna bought a sofa at the sale price of $1,344. The original price of the sofa was $1,920.

a. $576 b. 30%

62. Hiroshi bought a lawnmower at the sale price of $240. The original price of the lawnmower is $300.

In the following exercises, find a. the amount of the mark-up and b. the list price.

63. Daria bought a bracelet at original cost $16 to sell in her handicraft store. She marked the price up 45%. What was the list price of the bracelet?

a. $7.20 b. $23.20

64. Regina bought a handmade quilt at original cost $120 to sell in her quilt store. She marked the price up 55%. What was the list price of the quilt?

65. Tom paid $0.60 a pound for tomatoes to sell at his produce store. He added a 33% mark-up. What price did he charge his customers for the tomatoes?

a. $0.20 b. $0.80

66. Flora paid her supplier $0.74 a stem for roses to sell at her flower shop. She added an 85% mark-up. What price did she charge her customers for the roses?

67. Casey deposited $1,450 in a bank account that earned simple interest at an interest rate of 4%. How much interest was earned in two years?

68 . Terrence deposited $5,720 in a bank account that earned simple interest at an interest rate of 6%. How much interest was earned in four years?

69. Robin deposited $31,000 in a bank account that earned simple interest at an interest rate of 5.2%. How much interest was earned in three years?

70. Carleen deposited $16,400 in a bank account that earned simple interest at an interest rate of 3.9% How much interest was earned in eight years?

71. Hilaria borrowed $8,000 from her grandfather to pay for college. Five years later, she paid him back the $8,000, plus $1,200 interest. What was the rate of simple interest?

72. Kenneth lent his niece $1,200 to buy a computer. Two years later, she paid him back the $1,200, plus $96 interest. What was the rate of simple interest?

73. Lebron lent his daughter $20,000 to help her buy a condominium. When she sold the condominium four years later, she paid him the $20,000, plus $3,000 interest. What was the rate of simple interest?

74. Pablo borrowed $50,000 to start a business. Three years later, he repaid the $50,000, plus $9,375 interest. What was the rate of simple interest?

75. In 10 years, a bank account that paid 5.25% simple interest earned $18,375 interest. What was the principal of the account?

76. In 25 years, a bond that paid 4.75% simple interest earned $2,375 interest. What was the principal of the bond?

77. Joshua’s computer loan statement said he would pay $1,244.34 in simple interest for a three-year loan at 12.4%. How much did Joshua borrow to buy the computer?

78. Margaret’s car loan statement said she would pay $7,683.20 in simple interest for a five-year loan at 9.8%. How much did Margaret borrow to buy the car?

Everyday Math

79 . Tipping At the campus coffee cart, a medium coffee costs $1.65. MaryAnne brings $2.00 with her when she buys a cup of coffee and leaves the change as a tip. What percent tip does she leave?

80 . Tipping Four friends went out to lunch and the bill came to $53.75 They decided to add enough tip to make a total of $64, so that they could easily split the bill evenly among themselves. What percent tip did they leave?

Writing Exercises

81. What has been your past experience solving word problems? Where do you see yourself moving forward?

82. Without solving the problem “44 is 80% of what number” think about what the solution might be. Should it be a number that is greater than 44 or less than 44? Explain your reasoning.

83. After returning from vacation, Alex said he should have packed 50% fewer shorts and 200% more shirts. Explain what Alex meant.

84. Because of road construction in one city, commuters were advised to plan that their Monday morning commute would take 150% of their usual commuting time. Explain what this means.

a. After completing the exercises, use this checklist to evaluate your mastery of the objective of this section.

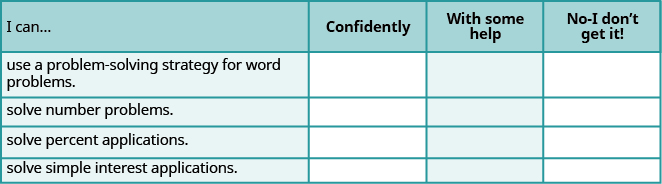
b. After reviewing this checklist, what will you do to become confident for all objectives?

Hybrid Classical-Quantum Optimization Techniques for Solving Mixed-Integer Programming Problems in Production Scheduling

Ieee account.

• Change Username/Password
• Update Address

Purchase Details

• Payment Options
• Order History
• View Purchased Documents

Profile Information

• Communications Preferences
• Profession and Education
• Technical Interests
• US & Canada: +1 800 678 4333
• Worldwide: +1 732 981 0060
• Contact & Support
• About IEEE Xplore
• Accessibility
• Terms of Use
• Nondiscrimination Policy
• Privacy & Opting Out of Cookies

A not-for-profit organization, IEEE is the world's largest technical professional organization dedicated to advancing technology for the benefit of humanity. © Copyright 2024 IEEE - All rights reserved. Use of this web site signifies your agreement to the terms and conditions.