12.2 problem solving with right triangles

Right Triangles

Rules, Formula and more

Pythagorean Theorem

The sum of the squares of the lengths of the legs equals the square of the length of the hypotenuse .

Usually, this theorem is expressed as $$ A^2 + B^2 = C^2 $$ .

Right Triangle Properties

A right triangle has one $$ 90^{\circ} $$ angle ($$ \angle $$ B in the picture on the left) and a variety of often-studied formulas such as:

• The Pythagorean Theorem
• Trigonometry Ratios (SOHCAHTOA)
• Pythagorean Theorem vs Sohcahtoa (which to use)

SOHCAHTOA only applies to right triangles ( more here ) .

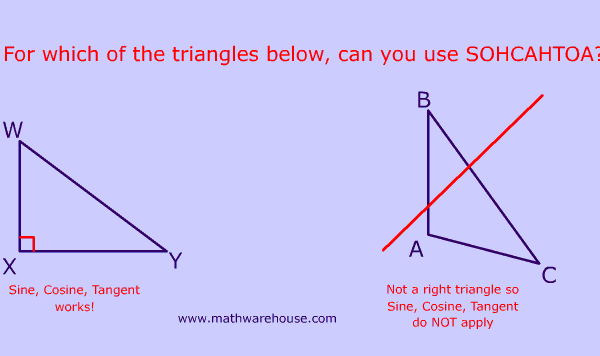
A Right Triangle's Hypotenuse

The hypotenuse is the largest side in a right triangle and is always opposite the right angle.

In the triangle above, the hypotenuse is the side AB which is opposite the right angle, $$ \angle C $$.

Online tool calculates the hypotenuse (or a leg) using the Pythagorean theorem.

Practice Problems

Below are several practice problems involving the Pythagorean theorem, you can also get more detailed lesson on how to use the Pythagorean theorem here .

Find the length of side t in the triangle on the left.

Substitute the two known sides into the Pythagorean theorem's formula : A² + B² = C²

What is the value of x in the picture on the left?

Set up the Pythagorean Theorem : 14 2 + 48 2 = x 2 2,500 = X 2

$$ x = \sqrt{2500} = 50 $$

$$ x^2 = 21^2 + 72^2 \\ x^2= 5625 \\ x = \sqrt{5625} \\ x =75 $$

Find the length of side X in the triangle on on the left?

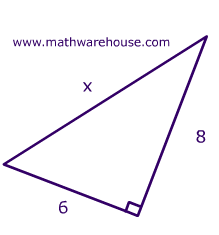
Substitue the two known sides into the pythagorean theorem's formula : $$ A^2 + B^2 = C^2 \\ 8^2 + 6^2 = x^2 \\ x = \sqrt{100}=10 $$

What is x in the triangle on the left?

x 2 + 4 2 = 5 2 x 2 + 16 = 25 x 2 = 25 - 16 = 9 x = 3

Ultimate Math Solver (Free) Free Algebra Solver ... type anything in there!

Popular pages @ mathwarehouse.com.

10.8 Right Triangle Trigonometry

Learning objectives.

After completing this section, you should be able to:

• Apply the Pythagorean Theorem to find the missing sides of a right triangle.
• Apply the 30 ∘ - 60 ∘ - 90 ∘ 30 ∘ - 60 ∘ - 90 ∘ and 45 ∘ - 45 ∘ - 90 ∘ 45 ∘ - 45 ∘ - 90 ∘ right triangle relationships to find the missing sides of a triangle.
• Apply trigonometric ratios to find missing parts of a right triangle.
• Solve application problems involving trigonometric ratios.

This is another excerpt from Raphael’s The School of Athens. The man writing in the book represents Pythagoras, the namesake of one of the most widely used formulas in geometry, engineering, architecture, and many other fields, the Pythagorean Theorem. However, there is evidence that the theorem was known as early as 1900–1100 BC by the Babylonians. The Pythagorean Theorem is a formula used for finding the lengths of the sides of right triangles.

Born in Greece, Pythagoras lived from 569–500 BC. He initiated a cult-like group called the Pythagoreans, which was a secret society composed of mathematicians, philosophers, and musicians. Pythagoras believed that everything in the world could be explained through numbers. Besides the Pythagorean Theorem, Pythagoras and his followers are credited with the discovery of irrational numbers, the musical scale, the relationship between music and mathematics, and many other concepts that left an immeasurable influence on future mathematicians and scientists.

The focus of this section is on right triangles. We will look at how the Pythagorean Theorem is used to find the unknown sides of a right triangle, and we will also study the special triangles, those with set ratios between the lengths of sides. By ratios we mean the relationship of one side to another side. When you think about ratios, you should think about fractions. A fraction is a ratio, the ratio of the numerator to the denominator. Finally, we will preview trigonometry. We will learn about the basic trigonometric functions, sine, cosine and tangent, and how they are used to find not only unknown sides but unknown angles, as well, with little information.

Pythagorean Theorem

The Pythagorean Theorem is used to find unknown sides of right triangles. The theorem states that the sum of the squares of the two legs of a right triangle equals the square of the hypotenuse (the longest side of the right triangle).

The Pythagorean Theorem states

where a a and b b are two sides (legs) of a right triangle and c c is the hypotenuse, as shown in Figure 10.138 .

For example, given that side a = 6 , a = 6 , and side b = 8 , b = 8 , we can find the measure of side c c using the Pythagorean Theorem. Thus,

Example 10.64

Using the pythagorean theorem.

Find the length of the missing side of the triangle ( Figure 10.139 ).

Using the Pythagorean Theorem , we have

When we take the square root of a number, the answer is usually both the positive and negative root. However, lengths cannot be negative, which is why we only consider the positive root.

Your Turn 10.64

The applications of the Pythagorean Theorem are countless, but one especially useful application is that of distance. In fact, the distance formula stems directly from the theorem. It works like this:

In Figure 10.140 , the problem is to find the distance between the points ( − 3 , − 1 ) ( − 3 , − 1 ) and ( 3 , 2 ) . ( 3 , 2 ) . We call the length from point ( − 3 , − 1 ) ( − 3 , − 1 ) to point ( 3 , − 1 ) ( 3 , − 1 ) side a a , and the length from point ( 3 , − 1 ) ( 3 , − 1 ) to point ( 3 , 2 ) ( 3 , 2 ) side b b . To find side c c , we use the distance formula and we will explain it relative to the Pythagorean Theorem. The distance formula is d = ( x 2 − x 1 ) 2 + ( y 2 − y 1 ) 2 , d = ( x 2 − x 1 ) 2 + ( y 2 − y 1 ) 2 , such that ( x 2 − x 1 ) ( x 2 − x 1 ) is a substitute for a a in the Pythagorean Theorem and is equal to 3 − ( − 3 ) = 6 ; 3 − ( − 3 ) = 6 ; and ( y 2 − y 1 ) ( y 2 − y 1 ) is a substitute for b b in the Pythagorean Theorem and is equal to 2 − ( − 1 ) = 3. 2 − ( − 1 ) = 3. When we plug in these numbers to the distance formula, we have

Thus, d = c d = c , the hypotenuse, in the Pythagorean Theorem.

Example 10.65

Calculating distance using the distance formula.

You live on the corner of First Street and Maple Avenue, and work at Star Enterprises on Tenth Street and Elm Drive ( Figure 10.141 ). You want to calculate how far you walk to work every day and how it compares to the actual distance (as the crow flies). Each block measures 200 ft by 200 ft.

You travel 7 blocks south and 9 blocks west. If each block measures 200 ft by 200 ft, then 9 ( 200 ) + 7 ( 200 ) = 1,800 ft + 1,400 ft = 3,200 ft 9 ( 200 ) + 7 ( 200 ) = 1,800 ft + 1,400 ft = 3,200 ft .

As the crow flies, use the distance formula. We have

Your Turn 10.65

Example 10.66, calculating distance with the pythagorean theorem.

The city has specific building codes for wheelchair ramps. Every vertical rise of 1 in requires that the horizontal length be 12 inches. You are constructing a ramp at your business. The plan is to make the ramp 130 inches in horizontal length and the slanted distance will measure approximately 132.4 inches ( Figure 10.142 ). What should the vertical height be?

The Pythagorean Theorem states that the horizontal length of the base of the ramp, side a , is 130 in. The length of c , or the length of the hypotenuse, is 132.4 in. The length of the height of the triangle is side b .

Then, by the Pythagorean Theorem , we have:

If you construct the ramp with a 25 in vertical rise, will it fulfill the building code? If not, what will have to change?

The building code states 12 in of horizontal length for each 1 in of vertical rise. The vertical rise is 25 in, which means that the horizontal length has to be 12 ( 25 ) = 300 in . 12 ( 25 ) = 300 in . So, no, this will not pass the code. If you must keep the vertical rise at 25 in, what will the other dimensions have to be? Since we need a minimum of 300 in for the horizontal length:

The new ramp will look like Figure 10.143 .

Your Turn 10.66

30 ∘ - 60 ∘ - 90 ∘ 30 ∘ - 60 ∘ - 90 ∘ triangles.

In geometry, as in all fields of mathematics, there are always special rules for special circumstances. An example is the perfect square rule in algebra. When expanding an expression like ( 2 x + 5 y ) 2 , ( 2 x + 5 y ) 2 , we do not have to expand it the long way:

If we know the perfect square formula, given as

we can skip the middle step and just start writing down the answer. This may seem trivial with problems like ( a + b ) 2 . ( a + b ) 2 . However, what if you have a problem like ( 2 3 + 3 31.8 c 3 ) 2 ? ( 2 3 + 3 31.8 c 3 ) 2 ? That is a different story. Nevertheless, we use the same perfect square formula. The same idea applies in geometry. There are special formulas and procedures to apply in certain types of problems. What is needed is to remember the formula and remember the kind of problems that fit. Sometimes we believe that because a formula is labeled special, we will rarely have use for it. That assumption is incorrect. So, let us identify the 30 ∘ - 60 ∘ - 90 ∘ 30 ∘ - 60 ∘ - 90 ∘ triangle and find out why it is special. See Figure 10.144 .

We see that the shortest side is opposite the smallest angle, and the longest side, the hypotenuse, will always be opposite the right angle. There is a set ratio of one side to another side for the 30 ∘ - 60 ∘ - 90 ∘ 30 ∘ - 60 ∘ - 90 ∘ triangle given as 1 : 3 : 2 , 1 : 3 : 2 , or x : x 3 : 2 x . x : x 3 : 2 x . Thus, you only need to know the length of one side to find the other two sides in a 30 ∘ - 60 ∘ - 90 ∘ 30 ∘ - 60 ∘ - 90 ∘ triangle.

Example 10.67

Finding missing lengths in a 3 0 ∘ - 6 0 ∘ - 9 0 ∘ 3 0 ∘ - 6 0 ∘ - 9 0 ∘ triangle.

Find the measures of the missing lengths of the triangle ( Figure 10.145 ).

We can see that this is a 30 ∘ - 60 ∘ - 90 ∘ 30 ∘ - 60 ∘ - 90 ∘ triangle because we have a right angle and a 30 ∘ 30 ∘ angle. The remaining angle, therefore, must equal 60 ∘ . 60 ∘ . Because this is a special triangle, we have the ratios of the sides to help us identify the missing lengths. Side a a is the shortest side, as it is opposite the smallest angle 30 ∘ , 30 ∘ , and we can substitute a = x . a = x . The ratios are x : x 3 : 2 x . x : x 3 : 2 x . We have the hypotenuse equaling 10, which corresponds to side c c , and side c c is equal to 2 x x . Now, we must solve for x x :

Side b b is equal to x 3 x 3 or 5 3 . 5 3 . The lengths are 5 , 5 3 , 10. 5 , 5 3 , 10.

Your Turn 10.67

Example 10.68, applying 3 0 ∘ - 6 0 ∘ - 9 0 ∘ 3 0 ∘ - 6 0 ∘ - 9 0 ∘ triangle to the real world.

A city worker leans a 40-foot ladder up against a building at a 30 ∘ 30 ∘ angle to the ground ( Figure 10.146 ). How far up the building does the ladder reach?

We have a 30 ∘ - 60 ∘ - 90 ∘ 30 ∘ - 60 ∘ - 90 ∘ triangle, and the hypotenuse is 40 ft. This length is equal to 2 x x , where x x is the shortest side. If 2 x = 40 2 x = 40 , then x = 20 x = 20 . The ladder is leaning on the wall 20 ft up from the ground.

Your Turn 10.68

4 5 ∘ - 4 5 ∘ - 9 0 ∘ 4 5 ∘ - 4 5 ∘ - 9 0 ∘ triangles.

The 45 ∘ - 45 ∘ - 90 ∘ 45 ∘ - 45 ∘ - 90 ∘ triangle is another special triangle such that with the measure of one side we can find the measures of all the sides. The two angles adjacent to the 90 ∘ 90 ∘ angle are equal, and each measures 45 ∘ . 45 ∘ . If two angles are equal, so are their opposite sides. The ratio among sides is 1 : 1 : 2 , 1 : 1 : 2 , or x : x : x 2 , x : x : x 2 , as shown in Figure 10.147 .

Example 10.69

Finding missing lengths of a 4 5 ∘ - 4 5 ∘ - 9 0 ∘ 4 5 ∘ - 4 5 ∘ - 9 0 ∘ triangle.

Find the measures of the unknown sides in the triangle ( Figure 10.148 ).

Because we have a 45 ∘ - 45 ∘ - 90 ∘ 45 ∘ - 45 ∘ - 90 ∘ triangle, we know that the two legs are equal in length and the hypotenuse is a product of one of the legs and 2 . 2 . One leg measures 3, so the other leg, a a , measures 3. Remember the ratio of x : x : x 2 . x : x : x 2 . Then, the hypotenuse, c c , equals 3 2 . 3 2 .

Your Turn 10.69

Trigonometry functions.

Trigonometry developed around 200 BC from a need to determine distances and to calculate the measures of angles in the fields of astronomy and surveying. Trigonometry is about the relationships (or ratios) of angle measurements to side lengths in primarily right triangles. However, trigonometry is useful in calculating missing side lengths and angles in other triangles and many applications.

NOTE: You will need either a scientific calculator or a graphing calculator for this section. It must have the capability to calculate trigonometric functions and express angles in degrees.

Trigonometry is based on three functions. We title these functions using the following abbreviations:

• sin = sine sin = sine
• cos = cosine cos = cosine
• tan = tangent tan = tangent

Letting r = x 2 + y 2 , r = x 2 + y 2 , which is the hypotenuse of a right triangle, we have Table 10.1 . The functions are given in terms of x x , y y , and r r , and in terms of sides relative to the angle, like opposite, adjacent, and the hypotenuse.

We will be applying the sine function, cosine function, and tangent function to find side lengths and angle measurements for triangles we cannot solve using any of the techniques we have studied to this point. In Figure 10.149 , we have an illustration mainly to identify r r and the sides labeled x x and y y .

An angle θ θ sweeps out in a counterclockwise direction from the positive x x -axis and stops when the angle reaches the desired measurement. That ray extending from the origin that marks θ ∘ θ ∘ is called the terminal side because that is where the angle terminates. Regardless of the information given in the triangle, we can find all missing sides and angles using the trigonometric functions. For example, in Figure 10.150 , we will solve for the missing sides.

Let’s use the trigonometric functions to find the sides x x and y y . As long as your calculator mode is set to degrees, you do not have to enter the degree symbol. First, let’s solve for y y .

We have sin θ = y r , sin θ = y r , and θ = 60 ∘ . θ = 60 ∘ . Then,

Next, let’s find x x . This is the cosine function. We have cos θ = x r . cos θ = x r . Then,

Now we have all sides, 1 , 3 , 2. 1 , 3 , 2. You can also check the sides using the 30 ∘ - 60 ∘ - 90 ∘ 30 ∘ - 60 ∘ - 90 ∘ ratio of 1 : 3 : 2. 1 : 3 : 2. Table 10.2 is a list of common angles, which you should find helpful.

Example 10.70

Using trigonometric functions.

Find the lengths of the missing sides for the triangle ( Figure 10.151 ).

We have a 55 ∘ 55 ∘ angle, and the length of the triangle on the x x -axis is 6 units.

Step 1: To find the length of r r , we can use the cosine function, as cos θ = x r . cos θ = x r . We manipulate this equation a bit to solve for r r :

Step 2: We can use the Pythagorean Theorem to find the length of y y . Prove that your answers are correct by using other trigonometric ratios:

Step 3: Now that we have y y , we can use the sine function to prove that r r is correct. We have sin θ = y r . sin θ = y r .

Your Turn 10.70

To find angle measurements when we have two side measurements, we use the inverse trigonometric functions symbolized as sin − 1 , sin − 1 , cos − 1 , cos − 1 , or tan − 1 . tan − 1 . The –1 looks like an exponent, but it means inverse. For example, in the previous example, we had x = 6 x = 6 and r = 10.46. r = 10.46. To find what angle has these values, enter the values for the inverse cosine function cos − 1 ( x r ) cos − 1 ( x r ) in your calculator:

You can also use the inverse sine function and enter the values of sin − 1 ( y r ) sin − 1 ( y r ) in your calculator given y = 8.57 y = 8.57 and r = 10.46. r = 10.46. We have

Finally, we can also use the inverse tangent function. Recall tan θ = y x . tan θ = y x . We have

Example 10.71

Solving for lengths in a right triangle.

Solve for the lengths of a right triangle in which θ = 30 ∘ θ = 30 ∘ and r = 6 r = 6 ( Figure 10.152 ).

Step 1: To find side a a , we use the sine function:

Step 2: To find b b , we use the cosine function:

Step 3: Since this is a 30 ∘ - 60 ∘ - 90 ∘ 30 ∘ - 60 ∘ - 90 ∘ triangle and side b b should equal x 3 , x 3 , if we input 3 for x x , we have b = 3 3 . b = 3 3 . Put this in your calculator and you will get 3 3 = 5.196. 3 3 = 5.196.

Your Turn 10.71

Example 10.72, finding altitude.

A small plane takes off from an airport at an angle of 31.3 ∘ 31.3 ∘ to the ground. About two-thirds of a mile (3,520 ft) from the airport is an 1,100-ft peak in the flight path of the plane ( Figure 10.153 ). If the plane continues that angle of ascent, find its altitude when it is above the peak, and how far it will be above the peak.

To solve this problem, we use the tangent function:

The plane’s altitude when passing over the peak is 2,140 ft, and it is 1,040 ft above the peak.

Your Turn 10.72

Example 10.73, finding unknown sides and angles.

Suppose you have two known sides, but do not know the measure of any angles except for the right angle ( Figure 10.154 ). Find the measure of the unknown angles and the third side.

Step 1: We can find the third side using the Pythagorean Theorem:

Now, we have all three sides.

Step 2: To find θ , θ , we will first find sin θ . sin θ .

The angle θ θ is the angle whose sine is 2 13 . 2 13 .

Step 3: To find θ θ , we use the inverse sine function:

Step 4: To find the last angle, we just subtract: 180 ∘ − 90 ∘ − 33.7 ∘ = 56.3 ∘ 180 ∘ − 90 ∘ − 33.7 ∘ = 56.3 ∘ .

Your Turn 10.73

Angle of elevation and angle of depression.

Other problems that involve trigonometric functions include calculating the angle of elevation and the angle of depression . These are very common applications in everyday life. The angle of elevation is the angle formed by a horizontal line and the line of sight from an observer to some object at a higher level. The angle of depression is the angle formed by a horizontal line and the line of sight from an observer to an object at a lower level.

Example 10.74

Finding the angle of elevation.

A guy wire of length 110 meters runs from the top of an antenna to the ground ( Figure 10.155 ). If the angle of elevation of an observer to the top of the antenna is 43 ∘ , 43 ∘ , how high is the antenna?

We are looking for the height of the tower. This corresponds to the y y -value, so we will use the sine function:

The tower is 75 m high.

Your Turn 10.74

Example 10.75, finding angle of elevation.

You are sitting on the grass flying a kite on a 50-foot string ( Figure 10.156 ). The angle of elevation is 60 ∘ . 60 ∘ . How high above the ground is the kite?

We can solve this using the sine function, sin θ = o p p h y p . sin θ = o p p h y p .

Your Turn 10.75

People in mathematics, pythagoras and the pythagoreans.

The Pythagorean Theorem is so widely used that most people assume that Pythagoras (570–490 BC) discovered it. The philosopher and mathematician uncovered evidence of the right triangle concepts in the teachings of the Babylonians dating around 1900 BC. However, it was Pythagoras who found countless applications of the theorem leading to advances in geometry, architecture, astronomy, and engineering.

Among his accolades, Pythagoras founded a school for the study of mathematics and music. Students were called the Pythagoreans, and the school’s teachings could be classified as a religious indoctrination just as much as an academic experience. Pythagoras believed that spirituality and science coexist, that the intellectual mind is superior to the senses, and that intuition should be honored over observation.

Pythagoras was convinced that the universe could be defined by numbers, and that the natural world was based on mathematics. His primary belief was All is Number. He even attributed certain qualities to certain numbers, such as the number 8 represented justice and the number 7 represented wisdom. There was a quasi-mythology that surrounded Pythagoras. His followers thought that he was more of a spiritual being, a sort of mystic that was all-knowing and could travel through time and space. Some believed that Pythagoras had mystical powers, although these beliefs were never substantiated.

Pythagoras and his followers contributed more ideas to the field of mathematics, music, and astronomy besides the Pythagorean Theorem. The Pythagoreans are credited with the discovery of irrational numbers and of proving that the morning star was the planet Venus and not a star at all. They are also credited with the discovery of the musical scale and that different strings made different sounds based on their length. Some other concepts attributed to the Pythagoreans include the properties relating to triangles other than the right triangle, one of which is that the sum of the interior angles of a triangle equals 180 ∘ . 180 ∘ . These geometric principles, proposed by the Pythagoreans, were proven 200 years later by Euclid.

A Visualization of the Pythagorean Theorem

In Figure 10.157 , which is one of the more popular visualizations of the Pythagorean Theorem, we see that square a a is attached to side a a ; square b b is attached to side b b ; and the largest square, square c c , is attached to side c c . Side a a measures 3 cm in length, side b b measures 4 cm in length, and side c c measures 5 cm in length. By definition, the area of square a a measures 9 square units, the area of square b b measures 16 square units, and the area of square c c measures 25 square units. Substitute the values given for the areas of the three squares into the Pythagorean Theorem and we have

Thus, the sum of the squares of the two legs of a right triangle is equal to the square of the hypotenuse, as stated in the Pythagorean Theorem.

Check Your Understanding

Section 10.8 exercises.

As an Amazon Associate we earn from qualifying purchases.

This book may not be used in the training of large language models or otherwise be ingested into large language models or generative AI offerings without OpenStax's permission.

Want to cite, share, or modify this book? This book uses the Creative Commons Attribution License and you must attribute OpenStax.

Access for free at https://openstax.org/books/contemporary-mathematics/pages/1-introduction

• Authors: Donna Kirk
• Publisher/website: OpenStax
• Book title: Contemporary Mathematics
• Publication date: Mar 22, 2023
• Location: Houston, Texas
• Book URL: https://openstax.org/books/contemporary-mathematics/pages/1-introduction
• Section URL: https://openstax.org/books/contemporary-mathematics/pages/10-8-right-triangle-trigonometry

© Dec 21, 2023 OpenStax. Textbook content produced by OpenStax is licensed under a Creative Commons Attribution License . The OpenStax name, OpenStax logo, OpenStax book covers, OpenStax CNX name, and OpenStax CNX logo are not subject to the Creative Commons license and may not be reproduced without the prior and express written consent of Rice University.

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons
• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

5.5: Right Triangle Trigonometry

• Last updated
• Save as PDF
• Page ID 13862

• David Lippman & Melonie Rasmussen
• The OpenTextBookStore

In Section 5.3 we were introduced to the sine and cosine function as ratios of the sides of a triangle drawn inside a circle, and spent the rest of that section discussing the role of those functions in finding points on the circle. In this section, we return to the triangle, and explore the applications of the trigonometric functions to right triangles where circles may not be involved.

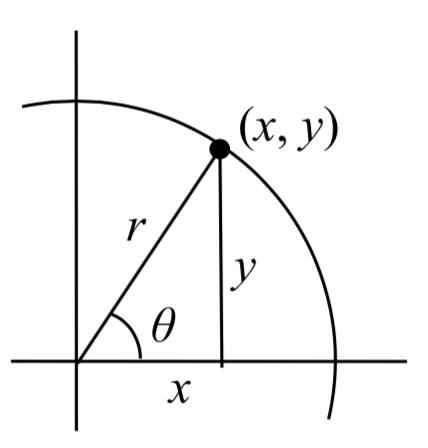
\[\sin (\theta ) = \dfrac{y}{r}\nonumber\]

\[\cos(\theta ) = \dfrac{x}{r}\nonumber\]

Separating the triangle from the circle, we can make equivalent but more general definitions of the sine, cosine, and tangent on a right triangle. On the right triangle, we will label the hypotenuse as well as the side opposite the angle and the side adjacent (next to) the angle.

RIGHT TRIANGLE RELATIONSHIPS

Given a right triangle with an angle of \(\theta\)

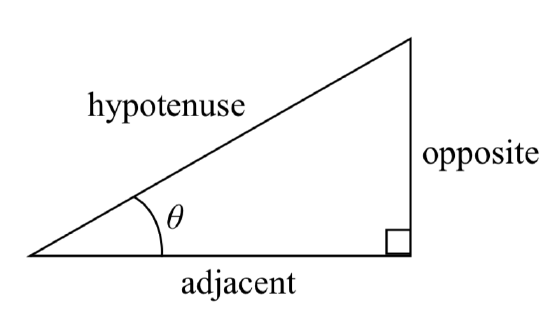
\[\text{sin} (\theta) = \dfrac{\text{opposite}}{\text{hypotenuse}}\]

\[\text{cos} (\theta) = \dfrac{\text{adjacent}}{\text{hypotenuse}}\]

\[\text{tan} (\theta) = \dfrac{\text{opposite}}{\text{adjacent}}\]

A common mnemonic for remembering these relationships is SohCahToa, formed from the first letters of “ S ine is o pposite over h ypotenuse, C osine is a djacent over h ypotenuse, T angent is o pposite over a djacent.”

Example \(\PageIndex{1}\)

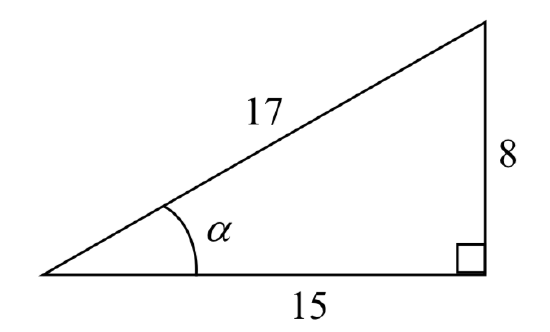
The side adjacent to the angle is 15, and the hypotenuse of the triangle is 17, so

\[\text{cos}(\alpha) = \dfrac{\text{adjacent}}{\text{hypotenuse}} = \dfrac{15}{17}\nonumber\]

When working with general right triangles, the same rules apply regardless of the orientation of the triangle. In fact, we can evaluate the sine and cosine of either of the two acute angles in the triangle.

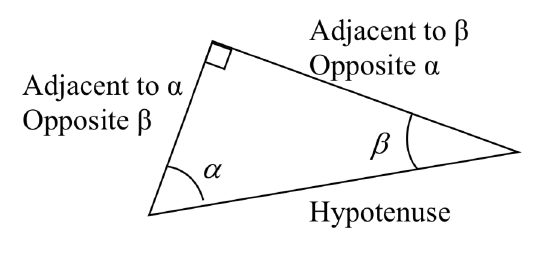
Example \(\PageIndex{2}\)

Using the triangle shown, evaluate cos(\(\alpha\)), sin(\(\alpha\)), cos(\(\beta\)), and sin(\(\beta\)),

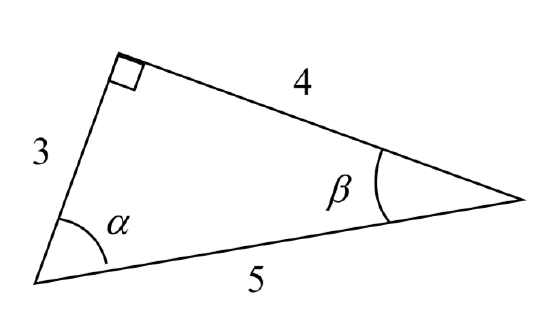
\[\text{cos}(\alpha) = \dfrac{\text{adjacent to } \alpha}{\text{hypotenuse}} = \dfrac{3}{5}\nonumber\]

\[\text{sin}(\alpha) = \dfrac{\text{opposite } \alpha}{\text{hypotenuse}} = \dfrac{4}{5}\nonumber\]

\[\text{cos}(\beta) = \dfrac{\text{adjacent to } \beta}{\text{hypotenuse}} = \dfrac{4}{5}\nonumber\]

\[\text{cos}(\beta) = \dfrac{\text{opposite } \beta}{\text{hypotenuse}} = \dfrac{3}{5}\nonumber\]

Exercise \(\PageIndex{1}\)

A right triangle is drawn with angle \(\alpha\) opposite a side with length 33, angle \(\beta\) opposite a side with length 56, and hypotenuse 65. Find the sine and cosine of \(\alpha\) and \(\beta\)

\[\text{sin} (\alpha) = \frac{33}{65}\nonumber\]

\[\text{cos} (\alpha) = \frac{56}{65}\nonumber\]

\[\text{sin} (\beta) = \frac{56}{65}\nonumber\]

\[\text{cos} (\beta) = \frac{33}{65}\nonumber\]

You may have noticed that in the above example that \(\cos (\alpha )=\sin (\beta )\) and \(\cos (\beta )=\sin (\alpha )\). This makes sense since the side opposite \(\alpha\) is also adjacent to \(\beta\). Since the three angles in a triangle need to add to \(\pi\), or 180 degrees, then the other two angles must add to \(\dfrac{\pi }{2}\), or 90 degrees, so \(\beta =\dfrac{\pi }{2} -\alpha\), and \(\alpha =\dfrac{\pi }{2} -\beta\). Since \(\cos (\alpha )=\sin (\beta )\), then \(\cos (\alpha )=\sin \left(\dfrac{\pi }{2} -\alpha \right)\).

COFUNCTION IDENTITIES

The confunction identities for sine and cosine are:

\[\text{cos} (\theta) = \text{sin} (\dfrac{\pi}{2} - \theta)\]

\[\text{sin} (\theta) = \text{cos} (\dfrac{\pi}{2} - \theta)\]

In the previous examples, we evaluated the sine and cosine on triangles where we knew all three sides of the triangle. Right triangle trigonometry becomes powerful when we start looking at triangles in which we know an angle but don’t know all the sides.

Example \(\PageIndex{3}\)

Find the unknown sides of the triangle pictured here.

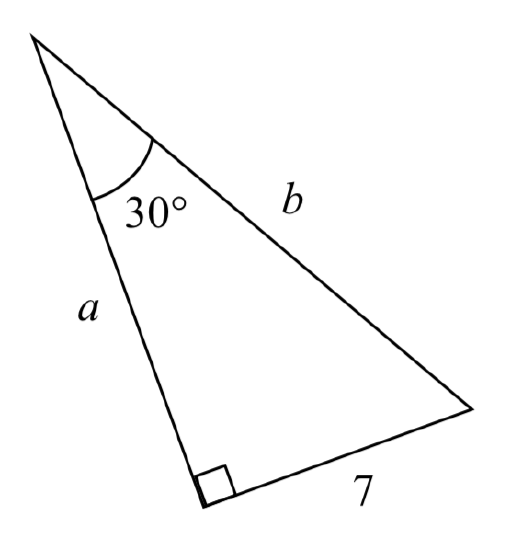
Since \(\text{sin} (\theta) = \dfrac{\text{opposite}}{\text{hypotenuse}}\). \(\text{sin}(30^{\circ}) = \dfrac{7}{b}\).

From this, we can solve for the side \(b\).

\[b\sin (30{}^\circ )=7\nonumber\] \[b=\dfrac{7}{\sin (30{}^\circ )}\nonumber\]

To obtain a value, we can evaluate the sine and simplify

\[b = \dfrac{7}{1/2} = 14\nonumber\]

To find the value for side \(a\), we could use the cosine, or simply apply the Pythagorean Theorem:

\[a^2 + 7^2 = b^2\nonumber\] \[a^2 + 7^2 = 14^2\nonumber\] \[a = \sqrt{147}\nonumber\]

Notice that if we know at least one of the non-right angles of a right triangle and one side, we can find the rest of the sides and angles.

Exercise \(\PageIndex{2}\)

A right triangle has one angle of \(\dfrac{\pi }{3}\) and a hypotenuse of 20. Find the unknown sides and angles of the triangle.

\[\text{cos} (\dfrac{\pi}{3}) = \dfrac{\text{adjacent}}{\text{hypoteuse}} = \dfrac{\text{Adj}}{20}\nonumber\] so, \[\text{adjacent} = 20 \text{cos} (\dfrac{\pi}{3}) = 20 (\dfrac{1}{2}) = 10\nonumber\]

\[\text{sin} (\dfrac{\pi}{3}) = \dfrac{\text{Opposite}}{\text{hypotenuse}} = \dfrac{\text{Opp}}{20}\nonumber\] so, \[\text{opposite} = 20 \text{sin} (\dfrac{\pi}{3}) = 20 (\dfrac{\sqrt{3}}{2}) = 10\sqrt{3}\nonumber\]

Missing angle = 180 - 90 - 60 = 30 degrees or \(\pi / 6\).

Example \(\PageIndex{4}\)

To find the height of a tree, a person walks to a point 30 feet from the base of the tree, and measures the angle from the ground to the top of the tree to be 57 degrees. Find the height of the tree.

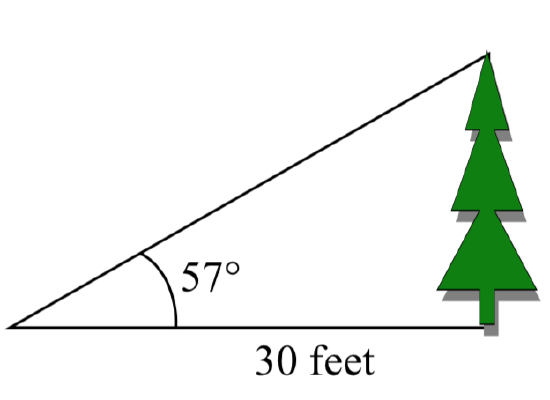
The trigonometric function which relates the side opposite of the angle and the side adjacent to the angle is the tangent.

\[\text{tan} (57^{\circ}) = \dfrac{\text{opposite}}{\text{adjacent}} = \dfrac{h}{30}\nonumber\] Solving for \(h\),

\[h=30\tan (57{}^\circ )\nonumber\] Using technology, we can approximate a value

\[h=30\tan (57{}^\circ )\approx 46.2\text{ feet}\nonumber\]

The tree is approximately 46 feet tall.

Example \(\PageIndex{5}\)

A person standing on the roof of a 100 foot tall building is looking towards a skyscraper a few blocks away, wondering how tall it is. She measures the angle of declination from the roof of the building to the base of the skyscraper to be 20 degrees and the angle of inclination to the top of the skyscraper to be 42 degrees.

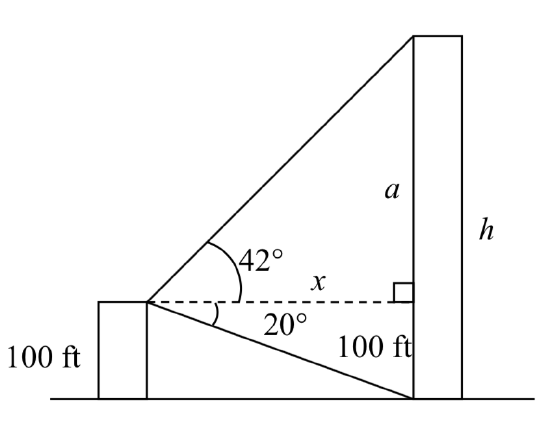
To start solving this problem, notice we have two right triangles. In the top triangle, we know one angle is 42 degrees, but we don’t know any of the sides of the triangle, so we don’t yet know enough to work with this triangle.

In the lower right triangle, we know one angle is 20 degrees, and we know the vertical height measurement of 100 ft. Since we know these two pieces of information, we can solve for the unknown distance \(x\).

\[\text{tan} (20^{\circ}) = \dfrac{\text{opposite}}{\text{adjacent}} = \dfrac{100}{x}\nonumber\] Solving for \(x\) \[x \text{tan} (20^{\circ}) = 100\nonumber\] \[x = \dfrac{100}{\text{tan} (20^{\circ})}\nonumber\]

Now that we have found the distance \(x\), we know enough information to solve the top right triangle.

\[\text{tan} (42^{\circ}) = \dfrac{\text{opposite}}{\text{adjacent}} = \dfrac{a}{x} = \dfrac{a}{100/\text{tan}(20^{circ})}\nonumber\] \[\text{tan} (42^{\circ}) = \dfrac{a\text{tan} (20^{\circ})}{100}\nonumber\] \[100 \text{tan} (42^{\circ}) = a\text{tan} (20^{\circ})\nonumber\] \[\dfrac{\text{tan} (42^{\circ})}{\text{tan} (20^{\circ})} = a\nonumber\]

Approximating a value,

\[a=\dfrac{100\tan (42{}^\circ )}{\tan (20{}^\circ )} \approx 247.4\text{ feet}\nonumber\]

Adding the height of the first building, we determine that the skyscraper is about 347 feet tall.

Important Topics of This Section

• SOH CAH TOA
• Cofunction identities
• Applications with right triangles

If you're seeing this message, it means we're having trouble loading external resources on our website.

If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.

To log in and use all the features of Khan Academy, please enable JavaScript in your browser.

Unit 5: Right triangles & trigonometry

About this unit, pythagorean theorem.

• Getting ready for right triangles and trigonometry (Opens a modal)
• Pythagorean theorem in 3D (Opens a modal)
• Pythagorean theorem with isosceles triangle (Opens a modal)
• Multi-step word problem with Pythagorean theorem (Opens a modal)
• Pythagorean theorem in 3D Get 3 of 4 questions to level up!
• Pythagorean theorem challenge Get 3 of 4 questions to level up!

Pythagorean theorem proofs

• Garfield's proof of the Pythagorean theorem (Opens a modal)
• Bhaskara's proof of the Pythagorean theorem (Opens a modal)
• Pythagorean theorem proof using similarity (Opens a modal)
• Another Pythagorean theorem proof (Opens a modal)

Special right triangles

• Special right triangles proof (part 1) (Opens a modal)
• Special right triangles proof (part 2) (Opens a modal)
• 30-60-90 triangle example problem (Opens a modal)
• Area of a regular hexagon (Opens a modal)
• Special right triangles review (Opens a modal)
• Special right triangles Get 3 of 4 questions to level up!

Ratios in right triangles

• Hypotenuse, opposite, and adjacent (Opens a modal)
• Side ratios in right triangles as a function of the angles (Opens a modal)
• Using similarity to estimate ratio between side lengths (Opens a modal)
• Using right triangle ratios to approximate angle measure (Opens a modal)
• Use ratios in right triangles Get 3 of 4 questions to level up!

Introduction to the trigonometric ratios

• Triangle similarity & the trigonometric ratios (Opens a modal)
• Trigonometric ratios in right triangles (Opens a modal)
• Trigonometric ratios in right triangles Get 3 of 4 questions to level up!

Solving for a side in a right triangle using the trigonometric ratios

• Solving for a side in right triangles with trigonometry (Opens a modal)
• Solve for a side in right triangles Get 3 of 4 questions to level up!

Solving for an angle in a right triangle using the trigonometric ratios

• Intro to inverse trig functions (Opens a modal)
• Solve for an angle in right triangles Get 3 of 4 questions to level up!

Sine & cosine of complementary angles

• Sine & cosine of complementary angles (Opens a modal)
• Using complementary angles (Opens a modal)
• Trig word problem: complementary angles (Opens a modal)
• Trig challenge problem: trig values & side ratios (Opens a modal)
• Relate ratios in right triangles Get 3 of 4 questions to level up!

Modeling with right triangles

• Right triangle word problem (Opens a modal)
• Angles of elevation and depression (Opens a modal)
• Right triangle trigonometry review (Opens a modal)
• Right triangles and trigonometry FAQ (Opens a modal)
• Right triangle trigonometry word problems Get 3 of 4 questions to level up!

Chapter 2: Trigonometric Ratios

Exercises: 2.2 Right Triangle Trigonometry

Exercises homework 2.2.

• Use measurements to calculate the trigonometric ratios for acute angles #1-10, 57-60
• Use trigonometric ratios to find unknown sides of right triangles #11-26
• Solve problems using trigonometric ratios #27-34, 41-46
• Use trig ratios to write equations relating the sides of a right triangle #35-40
• Use relationships among the trigonometric ratios #47-56, 61-68

Suggested Homework Problems

Here are two right triangles with a [latex]65 °[/latex] angle.

• Measure the sides [latex]AB[/latex] and [latex]BC[/latex] with a ruler. Use the lengths to estimate [latex]\sin 65°{.}[/latex]
• Measure the sides [latex]AD[/latex] and [latex]DE[/latex] with a ruler. Use the lengths to estimate [latex]\sin 65°{.}[/latex]
• Use your calculator to look up [latex]\sin 65°{.}[/latex] Compare your answers. How close were your estimates?

Use the figure in Problem 1 to calculate two estimates each for the cosine and tangent of [latex]65 °{.}[/latex] Compare your estimates to your calculator’s values for [latex]\cos 65°[/latex] and [latex]\tan 65°{.}[/latex]

Here are two right triangles with a [latex]40 °[/latex] angle.

• Measure the sides [latex]AB[/latex] and [latex]AC[/latex] with a ruler. Use the lengths to estimate [latex]\cos 40°{.}[/latex]
• Measure the sides [latex]AD[/latex] and [latex]AE[/latex] with a ruler. Use the lengths to estimate [latex]\cos 40°{.}[/latex]
• Use your calculator to look up [latex]\cos 40°{.}[/latex] Compare your answers. How close were your estimates?

Use the figure in Problem 2 to calculate two estimates each for the cosine and tangent of [latex]40 °{.}[/latex] Compare your estimates to your calculator’s values for [latex]\sin 40°[/latex] and [latex]\tan 40°{.}[/latex]

Exercise Group

For the right triangles in Problems 5–10,

• Find the length of the unknown side.
• Find the sine, cosine, and tangent of [latex]\theta \text{.}[/latex] Round your answers to four decimal places.

For Problems 11–16,

• Sketch and label the sides of a right triangle with angle [latex]\theta\text{.}[/latex]
• Sketch and label another right triangle with angle [latex]\theta[/latex] and longer sides.

[latex]\cos \theta = \dfrac{3}{5}[/latex]

[latex]\tan \theta = \dfrac{7}{2}[/latex]

[latex]\tan \theta = \dfrac{11}{4}[/latex]

[latex]\sin \theta = \dfrac{4}{9}[/latex]

[latex]\sin \theta = \dfrac{1}{9}[/latex]

[latex]\cos \theta = \dfrac{7}{8}[/latex]

For Problems 17–22, use one of the three trigonometric ratios to find the unknown side of the triangle. Round your answer to hundredths.

For Problems 23–26, sketch and label a right triangle with the given properties.

One angle is [latex]40°{,}[/latex] the side opposite that angle is 8 inches

One angle is [latex]65°{,}[/latex] the side adjacent to that angle is 30 yards

One angle is [latex]28°{,}[/latex] the hypotenuse is 56 feet

One leg is [latex]15[/latex] meters, the hypotenuse is [latex]18[/latex] meters

For Problems 27–34,

• Sketch a right triangle that illustrates the situation. Label your sketch with the given information.
• Choose the appropriate trig ratio and write an equation, then solve the problem.

To measure the height of cloud cover, airport controllers fix a searchlight to shine a vertical beam on the clouds. The searchlight is [latex]120[/latex] yards from the office. A technician in the office measures the angle of elevation to the light on the cloud cover at [latex]54.8°{.}[/latex] What is the height of the cloud cover?

To measure the distance across a canyon, Evel first sights an interesting rock directly opposite on the other side. He then walks [latex]200[/latex] yards down the rim of the canyon and sights the rock again, this time at an angle of [latex]18.5°[/latex] from the canyon rim. What is the width of the canyon?

A salvage ship is searching for the wreck of a pirate vessel on the ocean floor. Using sonar, they locate the wreck at an angle of depression of [latex]36.2°{.}[/latex] The depth of the ocean at their location is [latex]260[/latex] feet. How far should they move so that they are directly above the wrecked vessel?

Ramps for wheelchairs should be no steeper than an angle of [latex]6°{.}[/latex] How much horizontal distance should be allowed for a ramp that rises [latex]5[/latex] feet in height?

The radio signal from a weather balloon indicates that it is [latex]1500[/latex] meters from a meteorologist on the ground. The angle of elevation to the balloon is [latex]48°{.}[/latex] What is the balloon’s altitude?

According to Chinese legend, around 200 BC, the general Han Xin used a kite to determine the distance from his location to an enemy palace. He then dug a secret tunnel which emerged inside the palace. When the kite was directly above the palace, its angle of elevation was [latex]27°[/latex] and the string to the kite was [latex]1850[/latex] feet long. How far did Han Xin’s troops have to dig?

A cable car on a ski lift traverses a horizontal distance of [latex]1800[/latex] meters at an angle of [latex]38°{.}[/latex] How long is the cable?

Zelda is building the loft on her summer cottage. At its central point, the height of the loft is [latex]8[/latex] feet, and the pitch of the roof should be [latex]24°{.}[/latex] How long should the rafters be?

For Problems 35–40, use a trig ratio to write an equation for [latex]x[/latex] in terms of [latex]\theta{.}[/latex]

For Problems 41–44, find the altitude of the triangle. Round your answer to two decimal places.

For Problems 45 and 46, find the length of the chord [latex]AB{.}[/latex] Round your answer to two decimal places.

For Problems 47–50, fill in the table.

• In each of the figures for Problems 47-50, what is the relationship between the angles [latex]\theta[/latex] and [latex]\phi{?}[/latex]
• Study the tables for Problems 47-50. What do you notice about the values of sine and cosine for the angles [latex]\theta[/latex] and [latex]\phi{?}[/latex] Explain why this is true.

There is a relationship between the tangent, the sine, and the cosine of any angle. Study the tables for Problems 47-50 to discover this relationship. Write your answer as an equation.

• Use the figure to explain what happens to [latex]\tan \theta[/latex] as [latex]\theta[/latex] increases, and why.
• Use the figure to explain what happens to [latex]\cos \theta[/latex] as [latex]\theta[/latex] increases, and why.
• What happens to [latex]\tan \theta[/latex] as [latex]\theta[/latex] increases?
• What value does your calculator give for [latex]\tan 90°{?}[/latex] Why?

Explain why it makes sense that [latex]\sin 0° = 0[/latex] and [latex]\sin 90° = 1{.}[/latex] Use a figure to illustrate your explanation.

Explain why it makes sense that [latex]\cos 0° = 1[/latex] and [latex]\cos 90° = 0{.}[/latex] Use a figure to illustrate your explanation

For Problems 57–60, explain why the trigonometric ratio is not correct.

[latex]\sin \theta = \dfrac{5}{9}[/latex]

[latex]\tan \theta = \dfrac{4}{7}[/latex]

[latex]\cos \theta = \dfrac{21}{20}[/latex]

[latex]\sin \theta = \dfrac{8}{10}[/latex]

For Problems 61–64, sketch and label a right triangle, then fill in the blank.

If [latex]\sin \theta = 0.2358\text{,}[/latex]  then [latex]\cos (90^{o} - \theta)=\underline{\qquad} \text{,}[/latex]

• If [latex]\cos \alpha = \dfrac{3}{11} \text{,}[/latex] then [latex]\underline{\qquad} (90° - \alpha) = \dfrac{3}{11}\text{.}[/latex]
• If [latex]\sin 42° = n\text{,}[/latex] then [latex]\cos \underline{\qquad} = n\text{.}[/latex]
• If [latex]\cos 13° = z\text{,}[/latex] then [latex]\sin \underline{\qquad} = z\text{.}[/latex]
• If [latex]\cos \beta = \dfrac{2}{\sqrt{7}}{,}[/latex] then [latex]\sin (90° - \beta) =\underline{\qquad} {.}[/latex]
• If [latex]\sin \phi = 0.693{,}[/latex] then [latex](90° - \phi) = 0.693{.}[/latex]
• If [latex]\cos 87° = p{,}[/latex] then [latex]\sin \underline{\qquad} = p{.}[/latex]
• If [latex]\sin 59° =w{,}[/latex] then [latex]\cos \underline{\qquad} = w{.}[/latex]
• If [latex]\sin \phi = \dfrac{5}{13}[/latex] and [latex]\cos \phi = \dfrac{12}{13}{,}[/latex] then [latex]\tan \phi =\underline{\qquad} {.}[/latex]
• If [latex]\cos \beta = \dfrac{1}{\sqrt{10}}{,}[/latex] and [latex]\sin \beta = \dfrac{3}{\sqrt{10}}{,}[/latex] then [latex]\tan \beta = \underline{\qquad}{.}[/latex]
• If [latex]\tan B = \dfrac{2}{\sqrt{5}}[/latex] and [latex]\cos B = \dfrac{\sqrt{5}}{3}{,}[/latex] then [latex]\sin B =\underline{\qquad}{.}[/latex]
• If [latex]\sin W = \sqrt{\dfrac{3}{7}}[/latex] and [latex]\tan W = \dfrac{\sqrt{3}}{2}{,}[/latex] then [latex]\cos W =\underline{\qquad}{.}[/latex]
• If [latex]\cos \theta = \dfrac{2}{\sqrt{10}}[/latex] and [latex]\sin \theta = \sqrt{\dfrac{3}{5}}{,}[/latex] then [latex]\tan \theta = \underline{\qquad}{.}[/latex]
• If [latex]\sin \alpha = \dfrac{\sqrt{2}}{4}{,}[/latex] and [latex]\cos \alpha =\dfrac{\sqrt{14}}{4}{,}[/latex] then [latex]\tan \alpha = \underline{\qquad}{.}[/latex]
• If [latex]\tan A = \dfrac{\sqrt{7}}{3}[/latex] and [latex]\cos A = \dfrac{3}{4}{,}[/latex] then [latex]\sin A =\underline{\qquad}{.}[/latex]
• If [latex]\sin V = \sqrt{\dfrac{10}{5}}[/latex] and [latex]\tan V = \dfrac{2}{5}{,}[/latex] then [latex]\cos V =\underline{\qquad}{.}[/latex]

Explain why the cosine of a [latex]73°[/latex] angle is always the same, no matter what size triangle the angle is in. Illustrate your explanation with a sketch.

• If you plotted the points in your table, would they lie on a straight line? Why or why not?
• What is the slope of the line through the origin and point [latex]P{?}[/latex]
• What is the tangent of the angle [latex]\theta{?}[/latex]
• On the same grid, sketch an angle whose tangent is [latex]\dfrac{8}{5}.[/latex]
• Use your calculator to complete the table. Rounded your answers to hundredths.
• Use the values of tan [latex]\theta[/latex] to sketch all the angles listed in the table. Locate the vertex of each angle at the origin and the initial side along the positive [latex]x[/latex]-axis.

Trigonometry Copyright © 2024 by Bimal Kunwor; Donna Densmore; Jared Eusea; and Yi Zhen. All Rights Reserved.

Share This Book

• Math Lessons
• Math Formulas
• Calculators

Math Calculators, Lessons and Formulas

It is time to solve your math problem

• HW Help (paid service)
• Right Triangle Calculator

Right triangle calculator

New service on Mathportal

You can hire our experts to do your math homework.

We provide complete, handwritten, step-by-step solutions.

Most popular calculators

• Factoring Polynomials
• Solving equations
• Rationalize Denominator
• Arithmetic sequences

Polynomial Calculators

• Polynomial Roots
• Synthetic Division
• Polynomial Operations
• Graphing Polynomials
• Expand & Simplify
• Generate From Roots

Rational Expressions

• Simplifying
• Multiplication / Division
• Addition / Subtraction

Radical Expressions

Solving equations.

• Quadratic Equations (with steps)
• Polynomial Equations
• Solving Equations - With Steps

Quadratic Equation

• Solving (with steps)
• Quadratic Plotter
• Factoring Trinomials
• Equilateral Triangle
• Right Triangle
• Oblique Triangle
• Square Calculator
• Rectangle Calculator
• Circle Calculator
• Hexagon Calculator
• Rhombus Calculator
• Trapezoid Calculator
• Triangular Prism

Complex Numbers

• Modulus, inverse, polar form
• Simplify Expression

Systems of equations

• Vectors (2D & 3D)
• Add, Subtract, Multiply
• Determinant Calculator
• Matrix Inverse
• Characteristic Polynomial
• Eigenvalues
• Eigenvectors
• Matrix Decomposition

Calculus Calculators

• Limit Calculator
• Derivative Calculator
• Integral Calculator

Sequences & Series

• Arithmetic Sequences
• Geometric Sequences
• Find n th Term

Analytic Geometry

• Distance and Midpoint
• Triangle Calculator
• Graphing Lines
• Lines Intersection
• Two Point Form
• Line-Point Distance
• Parallel/Perpendicular
• Circle Equation
• Circle From 3 Points
• Circle-line Intersection

Trigonometry

• Degrees to Radians
• Trig. Equations
• Long Division
• Evaluate Expressions
• Fraction Calculator
• Greatest Common Divisor GCD
• Least Common Multiple LCM
• Prime Factorization
• Scientific Notation
• Percentage Calculator
• Dec / Bin / Hex

Statistics and probability

• Probability Calculator
• Probability Distributions
• Descriptive Statistics
• Standard Deviation
• Z - score Calculator
• Normal Distribution
• T-Test Calculator
• Correlation & Regression

Financial Calculators

• Simple Interest
• Compound Interest
• Amortization Calculator
• Annuity Calculator

Other Calculators

• Work Problems

Hire MATHPORTAL experts to do math homework for you.

Prices start at $3 per problem.

Right triangle calculations

The calculator uses the following formulas to find the missing values of a right triangle:

Example 01 :

Find hypotenuse $ c $ of a right triangle if $ a = 4\,cm $ and $ b = 8\,cm $.

When we know two sides, we use the Pythagorean theorem to find the third one.

Example 02 :

Find the angle $\alpha$ of a right triangle if hypotenuse $ c = 14~cm$ and leg $ a = 8~cm$.

In order to find missing angle we can use the sine function

Related Calculators

Was this calculator helpful?

Please tell me how can I make this better.

Welcome to MathPortal. This website's owner is mathematician Miloš Petrović. I designed this website and wrote all the calculators, lessons, and formulas .

If you want to contact me, probably have some questions, write me using the contact form or email me on [email protected]

Email (optional)

Right Triangle Calculator

What is a right triangle (or right-angled triangle), hypotenuse calculator, how to find the area of a right triangle, other considerations when dealing with a right triangle, special triangles, special right triangles, right angled triangles and parallelograms, pythagorean triplets, triangles meet maths, shadows and right triangles (radius of the earth).

The right triangle calculator will help you find the lengths of the sides of a right-angled triangle . This triangle solver will also teach you how to find the area of a right triangle as well as give plenty of information about the practical uses of a right triangle.

First things first, let's explain what a right triangle is. The definition is very simple and might even seem obvious for those who already know it: a right-angled triangle is a triangle where one and only one of the angles is exactly 90° . The other two angles will clearly be smaller than the right angle because the sum of all angles in a triangle is always 180°.

In a right-angled triangle, we define the sides in a special way. The side opposing the right angle is always the biggest in the triangle and receives the name of "hypotenuse". The other two sides are called catheti. The relationship between the hypotenuse and each cathetus is straightforward, as we will see when we talk about Pythagoras' theorem .

If all you want to calculate is the hypotenuse of a right triangle, this page and its right triangle calculator will work just fine. However, we would also recommend using the dedicated tool we have developed at Omni Calculators: the hypotenuse calculator . The hypotenuse is opposite the right angle and can be solved by using the Pythagorean theorem. In a right triangle with cathetus a and b and with hypotenuse c , Pythagoras' theorem states that: a² + b² = c² .

To solve for c , take the square root of both sides to get c = √(b²+a²) . We can consider this extension of the Pythagorean theorem as a "hypotenuse formula". A Pythagorean theorem calculator is also an excellent tool for calculating the hypotenuse.

Let's now solve a practical example of what it would take to calculate the hypotenuse of a right triangle without using any calculators available at Omni:

• Obtain the values of a and b .
• Square a and b .
• Sum up both values: a² + b² .
• Take the square root of the result.
• The square root will yield positive and negative results. Since we are dealing with length, disregard the negative one.
• The resulting value is the value of the hypotenuse c .

Now let's see what the process would be using one of Omni's calculators , for example, the right triangle calculator on this web page:

• Insert the value of a and b into the calculator; and
• Obtain the value of c immediately;
• As a bonus, you will get the value of the area for such a triangle.

We have already seen that calculating the area of a right angle triangle is very easy with the right triangle calculator. At Omni Calculators, we have a calculator specifically designed for that purpose as well: area of a right triangle calculator . Let's now see a bit more in-depth how to calculate areas of right triangles.

The method for finding the area of a right triangle is quite simple. All that you need are the lengths of the base and the height . In a right triangle, the base and the height are the two sides that form the right angle. Since multiplying these two values together would give the area of the corresponding rectangle, and the triangle is half of that, the formula is:

area = ½ × base × height .

If you don't know the base or the height, you can find it using the Pythagorean theorem. Try the right triangle calculator to check your calculations or calculate the area of triangles with sides that have larger or decimal-value lengths.

Now we're gonna see other things that can be calculated from a right triangle using some of the tools available at Omni. The sides of a triangle have a certain gradient or slope. The formula for the slope is

slope = (y₂ - y₁)/(x₂ - x₁) .

So if the coordinates are (1,-6) and (4,8) , the slope of the segment is (8 + 6)/(4 - 1) = 14/3 . An easy way to determine if the triangle is right, and you just know the coordinates, is to see if the slopes of any two lines multiply to equal -1 .

There is an easy way to convert angles from radians to degrees and degrees to radians with the use of the angle conversion:

• If an angle is in radians – multiply by 180/π ; and
• If an angle is in degrees – multiply by π/180 .

Sometimes you may encounter a problem where two or even three side lengths are missing. In such cases, the right triangle calculator, hypotenuse calculator, and method on how to find the area of a right triangle won't help. You have to use trigonometric functions to solve for these missing pieces.

The right triangle is just one of the many special triangles that exist. These triangles have one or several special characteristics that make them unique. For example, as we have seen, the right triangle has a right angle and hence a hypotenuse, which makes it a unique kind of triangle. Aside from the right-angled triangle, there are other special triangles with interesting properties.

One of the most known special triangles is the equilateral triangle, which has three equal sides and all its angles are 60°. This makes it much simpler to make a triangle solver calculator evaluate different parameters of such a triangle.

Another of special triangles is the isosceles triangle, which has 2 sides of equal length , and hence two angles of the same size. As opposed to the equilateral triangle, isosceles triangles come in many different shapes.

There are many other special triangles. However, we will now take a look at a few very special right triangles that, besides being right-angled triangles, they have other unique properties that make them interesting.

The so-called "45 45 90" triangle is probably the most special among all the special right triangles. This is a right-angled triangle that is also an isosceles triangle . Both its catheti are of the same length (isosceles), and it also has the peculiarity that the non-right angles are exactly half the size of the right angle that gives the name to the right triangle.

This right triangle is the kind of triangle that you can obtain when you divide a square by its diagonal . That is why both catheti (sides of the square) are of equal length. For those interested in knowing more about the most special of the special right triangles, we recommend checking out the 45 45 90 triangle calculator made for this purpose.

Another fascinating triangle from the group of special right triangles is the so-called "30 60 90" triangle. The name comes from having one right angle (90°), then one angle of 30°, and another of 60°. These angles are special because of the values of their trigonometric functions (cosine, sine, tangent, etc.). The consequences of this can be seen and understood with the 30 60 90 triangle calculator , but for those who are too lazy to click the link, we will summarize some of them here . Assuming that the shorter side is of length a , the triangle follows:

• The second length is equal to a√3 ;
• The hypotenuse is 2a ;
• The area is equal to (a²√3)/2 ; and
• The perimeter equals a(3 + √3) .

It might seem at first glance that a right triangle and a parallelogram do not have anything in common. How can a triangle solver help you understand a parallelogram? The reality is that any parallelogram can be decomposed into 2 or more right triangles . Let's take an example of the rectangle, which is the easiest one to see it.

Imagine a rectangle, any rectangle. Now draw a trace on one of the diagonals of this rectangle. If we separate the rectangle by the diagonal, we will obtain two right-angled triangles . Looking at the triangles, there is no need to use the right triangle calculator to see that both are equal, so their areas will be the same. This means that the area of the rectangle is double that of each triangle .

If we think about the equations, it makes sense since the area of a rectangle of sides a and b is exactly area = a × b , while for the right triangle is area = base × height / 2 which, in this case, would mean area = a × b /2 . This is precisely what we already saw by just cutting the rectangle by the diagonal.

It was a simple example of a rectangle, but the same applies to the area of a square. For other parallelograms, the process becomes a bit more complicated (it might involve up to 4 right triangles of different sizes). Still, with a bit of skill, you can use the same idea and calculate the area of a parallelogram using right-angled triangles. You can, of course, be even more efficient and just use our calculator.

Geometry and polygons, especially triangles, always come together. The properties of some triangles, like right triangles, are usually interesting and shocking, even for non-mathematicians. We will now have a look at an interesting set of numbers very closely related to right-angled triangles that mathematicians love, and maybe you will too.

These sets of numbers are called the Pythagorean triplets and are sets of 3 integers (let's call them a , b , and c ) and satisfy the Pythagorean theorem: a² + b² = c² . That is, they could form a right triangle with sides of length a , b , and c . The amount of numbers that satisfy this relationship is limited, but mathematicians find joy in searching for new ones.

Aside from the curiosity factor of this relationship, it has some interesting properties that are exploited in cryptography . Given the applications that one might find for such sets of numbers, mathematicians have explored even beyond, using 4, 5… and more sets of numbers that satisfy a similar relation in which the sum of the squares of all the numbers except for one, give the square of the number that's left.

Also very connected to these Pythagorean triplets is the infamous Fermat's last theorem in which the almost legendary cryptic mathematician Pierre Fermat stated that there could not be a set of three integer numbers that would satisfy the relation: aⁿ + bⁿ = cⁿ for n bigger than 2. This conjecture was only proven in 1995, more than 300 years after it was first formulated , and it's considered one of the most important mathematical problems of the century.

We have talked a lot about triangles, particularly right triangles, and their applications in maths and geometry. What we haven't talked about yet is the usefulness of right triangles for calculating things in real life . It might seem like the applications outside of geometry are limited, but let's have a look at shadows.

Yes, shadows. The dark shade projected by an object when it is illuminated. If you were to look at the shape made by the shadow, the object, and the ground, you would notice that it is, in fact, a right-angled triangle! At least, it is when the object is perfectly vertical and the ground is horizontal. Most of the time, this is the case, or at least close enough. This means that we can use the right triangle calculator to find different pieces of information about objects under the sun. Let's see how.

Imagine that you have a building of which we want to know the height , but you cannot measure it directly because it's too high to drop a measuring tape from the top. What you can do is measure the length of the shadow on the street. Then, with the help of any angle-measuring tool and a piece of paper, you can find out the angle between the shadow and the ground. Knowing that the angle between the building and the ground is 90°, you can obtain the value of the height of the building.

Using this technique, you can measure the height of many objects as long as you have a bright sunny day or other light sources to illuminate the object. In fact, this used to be a very common measuring technique in the olden days. Probably the most interesting and mind-blowing use of right triangles is that of Eratosthenes, who managed to use right-angled triangles and shadows to measure the radius of the Earth , and now we are gonna explain how he did it.

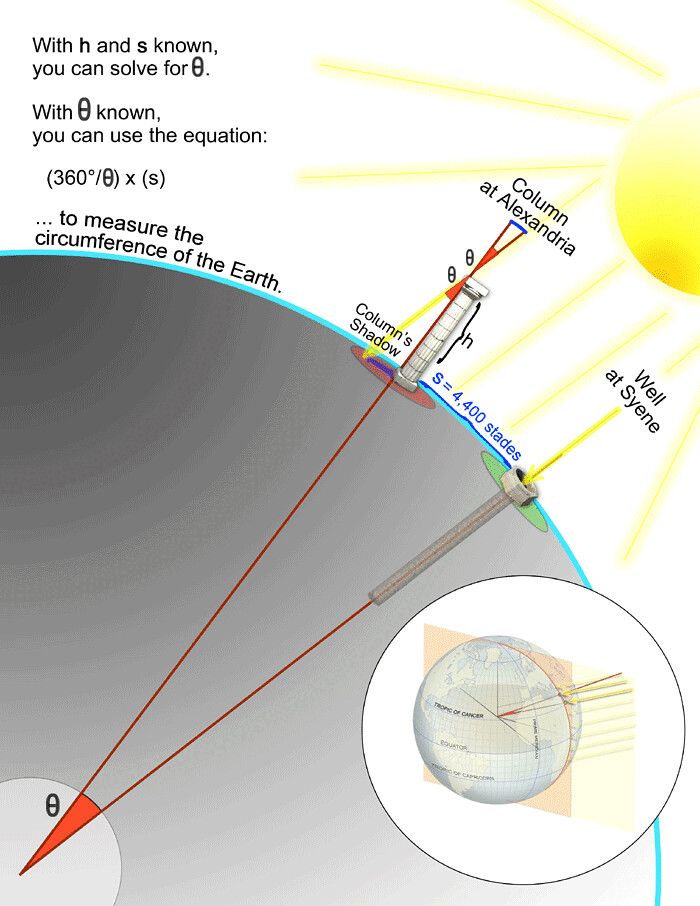
Eratosthenes noticed that on the summer solstice there was a place on Earth where the wells did not have a shadow at midday, i.e., the sun shone straight down onto them. Noting this, he set up a column of a known height at a known distance from that well and measured the size of the shadow created by the pole at noon on the solstice day. Then using right-angled triangles and trigonometry, he was able to determine the angle going from the center of the Earth between the well and the pole, as well as the radius of the Earth , based on the known distance between these two points.

It was quite an astonishing feat that now you can do much more easily, by just using the Omni calculators that we have created for you .

Which side lengths form a right triangle?

Side lengths a , b , c form a right triangle if, and only if, they satisfy a² + b² = c² . We say these numbers form a Pythagorean triple .

Do 2, 3, and 4 make a right triangle?

We have 4² = 16 and 2² + 3² = 4 + 9 = 13 , so the sum of squares of the two smaller numbers is NOT equal to the square of the largest number. That is, 2, 3, and 4 do not form a Pythagorean triple; in other words, there is no right triangle with sides 2, 3, and 4.

How do I find the circumcenter of a right angle triangle?

For a right-angled triangle, the circumcenter, i.e., the center of the circle circumscribed on the triangle, coincides with the midpoint of the triangle's longest side (its hypotenuse ).

How do I find the orthocenter of a right angle triangle?

The orthocenter of a right-angled triangle, i.e., the point where the triangle's altitudes intersect, coincides with the triangle's vertex of the right angle.

Black hole collision

Least common denominator, meat footprint.

• Biology (99)
• Chemistry (98)
• Construction (144)
• Conversion (292)
• Ecology (30)
• Everyday life (261)
• Finance (569)
• Health (440)
• Physics (508)
• Sports (104)
• Statistics (182)
• Other (181)
• Discover Omni (40)

Right Triangle Calculator

Please provide 2 values below to calculate the other values of a right triangle. If radians are selected as the angle unit, it can take values such as pi/3, pi/4, etc.

Related Triangle Calculator | Pythagorean Theorem Calculator

Right triangle

A right triangle is a type of triangle that has one angle that measures 90°. Right triangles, and the relationships between their sides and angles, are the basis of trigonometry.

In a right triangle, the side that is opposite of the 90° angle is the longest side of the triangle, and is called the hypotenuse. The sides of a right triangle are commonly referred to with the variables a, b, and c, where c is the hypotenuse and a and b are the lengths of the shorter sides. Their angles are also typically referred to using the capitalized letter corresponding to the side length: angle A for side a, angle B for side b, and angle C (for a right triangle this will be 90°) for side c, as shown below. In this calculator, the Greek symbols α (alpha) and β (beta) are used for the unknown angle measures. h refers to the altitude of the triangle, which is the length from the vertex of the right angle of the triangle to the hypotenuse of the triangle. The altitude divides the original triangle into two smaller, similar triangles that are also similar to the original triangle.

If all three sides of a right triangle have lengths that are integers, it is known as a Pythagorean triangle. In a triangle of this type, the lengths of the three sides are collectively known as a Pythagorean triple. Examples include: 3, 4, 5; 5, 12, 13; 8, 15, 17, etc.

Area and perimeter of a right triangle are calculated in the same way as any other triangle. The perimeter is the sum of the three sides of the triangle and the area can be determined using the following equation:

Special Right Triangles

30°-60°-90° triangle:

The 30°-60°-90° refers to the angle measurements in degrees of this type of special right triangle. In this type of right triangle, the sides corresponding to the angles 30°-60°-90° follow a ratio of 1:√ 3 :2. Thus, in this type of triangle, if the length of one side and the side's corresponding angle is known, the length of the other sides can be determined using the above ratio. For example, given that the side corresponding to the 60° angle is 5, let a be the length of the side corresponding to the 30° angle, b be the length of the 60° side, and c be the length of the 90° side.:

Angles: 30°: 60°: 90°

Ratio of sides: 1:√ 3 :2

Side lengths: a:5:c

Then using the known ratios of the sides of this special type of triangle:

As can be seen from the above, knowing just one side of a 30°-60°-90° triangle enables you to determine the length of any of the other sides relatively easily. This type of triangle can be used to evaluate trigonometric functions for multiples of π/6.

45°-45°-90° triangle:

The 45°-45°-90° triangle, also referred to as an isosceles right triangle, since it has two sides of equal lengths, is a right triangle in which the sides corresponding to the angles, 45°-45°-90°, follow a ratio of 1:1:√ 2 . Like the 30°-60°-90° triangle, knowing one side length allows you to determine the lengths of the other sides of a 45°-45°-90° triangle.

Angles: 45°: 45°: 90°

Ratio of sides: 1:1:√ 2

Side lengths: a:a:c

Given c= 5:

45°-45°-90° triangles can be used to evaluate trigonometric functions for multiples of π/4.

Chapter 12 - Lesson 12.2 Problem Solving with Right Triangles

Apr 05, 2019

380 likes | 386 Views

Chapter 12 - Lesson 12.2 Problem Solving with Right Triangles. HW: 12.2/1-20 . Finding the Sides of a Triangle. Remember: SOHCAHTOA. Review: Trig Ratios. First we will find the Sine, Cosine and Tangent ratios for Angle P. P.

Share Presentation

• theodolites
• elevation step
• elevation bottom horizontal
• horizontal ground distance

Presentation Transcript

Chapter 12 - Lesson 12.2 Problem Solving with Right Triangles HW: 12.2/1-20

Finding the Sides of a Triangle Remember: SOHCAHTOA

Review: Trig Ratios First we will find the Sine, Cosine and Tangent ratios for Angle P. P Next we will find the Sine, Cosine, and Tangent ratios for Angle Q 20 12 Adjacent Q 16 Opposite Remember SohCahToa

Solving Right Triangles Every right triangle has one right angle, two acute angles, one hypotenuse, and two legs. To Solve a Right Triangle means to determine the measures of all six parts.

Missing sides r and s, and angle S.

But what if you don’t know either of the acute angles? To solve those triangle we must use Inverse Trig Functions

Missing side….

What are the angles of elevation and depression and what is their relationship to right triangles?

ANGLE OF DEPRESSION Looking down from the horizontal observer Eye level Angle of depression cliffs object Sea level

ANGLE OF ELEVATION Looking up from the horizontal observer Eye level cliffs Angle of elevation object Sea level

If an observer sights an object above, the angle between a horizontal line and his or her line of sight is called an angle of elevation. If the line of sight is below the horizontal it is called the angle of depression. Angle of Depression Angle of Elevation

eye - level line of sight eye - level

The angles are equal – they are alternate interior angles eye - level line of sight eye - level

Angles of Elevation and Depression Top Horizontal Angle of Depression Line of Sight Angle of Elevation Bottom Horizontal Since the two horizontal lines are parallel, by Alternate Interior Angles the angle of depression must be equal to the angle of elevation.

Angles of Elevation and Depression line of sight

B h 250 A 21 m Example 1 The angle of elevation of building A to building B is 250. The distance between the buildings is 21 meters. Calculate how much taller Building B is than building A. Step 1: Draw a right angled triangle with the given information. Angle of elevation Step 2: Take care with placement of the angle of elevation Step 3: Set up the trig equation. Step 4: Solve the trig equation.

 80 m  60 m A boat is 60 meters out to sea. Madge is standing on a cliff 80 meters high. What is the angle of depression from the top of the cliff to the boat? Example 2 Step 1: Draw a right angled triangle with the given information. Angle of depression Step 2: Alternate interior angles place  inside the triangle. Step 3: Decide which trig ratio to use. Step 4: Use calculator to find the value of the unknown.

Plane 25 km h Marty is standing on level ground when he sees a plane directly overhead. The angle of elevation of the plane after it has travelled 25 km is 200. Calculate the altitude of the plane at this time. Example 3 Step 1: Draw a right angled triangle with the given information. 200 Step 2:Alternate interior angles places 200 inside the triangle. Angle of elevation 200 Step 3: Decide which trig ratio to use. Step 4: Use calculator to find the value of the unknown. (nearest km)

5m 650 450 P K p k Example 4 Kate and Petra are on opposite sides of a tree. The angle of elevation to the top of the tree from Kate is 45o and from Petra is 65o. If the tree is 5 m tall, who is closer to the tree, Kate or Petra? Kate Petra Answer Therefore, Petra is closer to the tree, since the distance is shorter.

Bird 400 200 2 m Car Example 5 Maryann is peering outside her window. From her window she sees her car and a bird hovering above her car. The angle of depression of Maryann’s car is 200 whilst the angle of elevation to the bird is 400. If Maryann’s window is 2m off the ground, what is the bird’s altitude at that moment? Step 1: Draw a diagram Step 2: Set up the trig equations in two parts. Find d first, then b. Step 3: Solve the equations and answer the question. b d Therefore, The bird is 6.6 m (2 + 4.6) from the ground at that moment.

Your Turn 1: You sight a rock climber on a cliff at a 32oangle of elevation. The horizontal ground distance to the cliff is 1000 ft. Find the line of sight distance to the rock climber. x 1000 ft

Your Turn 2: An airplane pilots sights a life raft at a 26o angle of depression. The airplane’s altitude is 3 km. What is the airplane’s surface distance dfrom the raft? 3 km d

FYI: Theodolite Theodolite is a precision instrument for measuring angles in the horizontal and vertical planes. Theodolites are mainly used for surveying applications, and have been adapted for specialized purposes in fields like meteorology and rocket launch technology. When the telescope is pointed at a target object, the angle of each of these axes can be measured with great precision Theodolites are still used today for ultra high precision optical alignment and measurement

x 200 tan 35° = x = 200 • tan 35° Your Turn 3: A surveyor stands 200 ft from a building to measure its height with a 5-ft tall theodolite. The angle of elevation to the top of the building is 35°. How tall is the building? So x ≈ 140 To find the height of the building, add the height of the Theodolite, which is 5 ft tall. The building is about 140 ft + 5 ft, or 145 ft tall.

Your Turn 4: 3500 x ft sin 2° = 3500 ft sin 2° x ft = An airplane flying 3500 ft above ground begins a 2° descent to land at an airport. How many miles from the airport is the airplane when it starts its descent? x ft ≈ 100,287.9792 ft x miles ≈ 18.9939 miles ≈ 19 miles The airplane is about 19 mi from the airport when it starts its descent.

Your Turn 5: A 6-ft man stands 12 ft from the base of a tree. The angle of elevation from his eyes to the top of the tree is 40°. 1. About how tall is the tree? 2. If the man releases a pigeon that flies directly to the top of the tree, about how far will it fly? 3. What is the angle of depression from the treetop to the man’s eyes? about 16 ft about 15.7 ft 40°

Your Turn 6: Step 1: Draw a triangle to fit problem Step 3: Identify trig function to use 30.5 = 25 + 5.5 Step 2: Label sides from angle’s view opp Step 4: Set up equation 27° adj x 30.5 tan 27° = ------- x Step 5: Solve for variable S  O / H C  A / H T  O / A x tan 27° = 30.5 x = (30.5) / (tan 27°) x = 59.9 CIRCUS ACTS. At the circus, a person in the audience watches the high-wire routine. A 5-foot-6-inch tall acrobat is standing on a platform that is 25 feet off the ground. How far is the audience member from the base of the platform, if the angle of elevation from the audience member’s line of sight to the top of the acrobat is 27°?

Your Turn 7: 37 = 32 + 6 x° 45 = 50 - 5 DIVING At a diving competition, a 6-foot-tall diver stands atop the 32-foot platform. The front edge of the platform projects 5 feet beyond the ends of the pool. The pool itself is 50 feet in length. A camera is set up at the opposite end of the pool even with the pool’s edge. If the camera is angled so that its line of sight extends to the top of the diver’s head, what is the camera’s angle of elevation to the nearest degree?

Your Turn 8: From a point 80m from the base of a tower, the angle of elevation is 28˚. How tall is the tower to the nearest meter? x 28˚ 80m tan 28˚ = 80 (tan 28˚) = x 80 (.5317) = x x ≈ 42.5m is the height of the tower

Your Turn 8: A ladder that is 20 ft is leaning against the side of a building. If the angle formed between the ladder and ground is 75˚, how far is the bottom of the ladder from the base of the building? 20 building ladder 75˚ x cos 75˚ = 20 (cos 75˚) = x 20 (.2588) = x x ≈ 5.2ft from the base of the building

Your Turn 9: When the sun is 62˚ above the horizon, a building casts a shadow 18m long. How tall is the building? x 62˚ 18 shadow tan 62˚ = 18 (tan 62˚) = x 18 (1.8807) = x x ≈ 33.9m is the height of the building

Your Turn 10: A kite is flying at an angle of elevation of about 55˚. Ignoring the sag in the string, find the height of the kite if 85m of string have been let out. kite 85 x string 55˚ sin 55˚ = 85 (sin 55˚) = x 85 (.8192) = x x ≈ 69.6m is the height of the kite

Your Turn 11: A 5.5 foot person standing 10 feet from a street light casts a 14 foot shadow. What is the height of the streetlight? 5.5 x˚ 10 14 shadow 1st find the angle of elevation 2nd use the angle to find the height of the light. tan x˚ = x° ≈ 21.45° height = 9.43 feet

Your Turn 12: The angle of depression from the top of a tower to a boulder on the ground is 38º. If the tower is 25m high, how far from the base of the tower is the boulder? 38º angle of depression 25 Alternate Interior Angles are congruent 38º x

• More by User

9.6 Solving Right Triangles

9.6 Solving Right Triangles. Geometry Mrs. Spitz Spring 2005. Objectives/Assignment. Solve a right triangle. Use right triangles to solve real-life problems, such as finding the glide angle and altitude of a space shuttle.

313 views • 16 slides

Solving Right Triangles

Solving Right Triangles. Geometry Mrs. Spitz Spring 2005. Objectives/Assignment. Solve a right triangle. Use right triangles to solve real-life problems, such as finding the glide angle and altitude of a space shuttle.

157 views • 14 slides

Lesson 9.1 Use Trigonometry with Right Triangles

Lesson 9.1 Use Trigonometry with Right Triangles. Standard Accessed: Students will prove, apply, and model trigonometric functions and ratios. Warm-Up. Lesson Presentation. Lesson Quiz. Warm-Up.

555 views • 13 slides

Trigonometry Functions And Solving Right Triangles

Trigonometry Functions And Solving Right Triangles. Next Slide. Title Page. Table OF Contents. Table of Content s. What are the Trigonometry Functions and how are they used. What do you need to solve a right Triangle using Trig. Functions. Sine Function. Cosine Function.

398 views • 24 slides

5-5 Solving Right Triangles

5-5 Solving Right Triangles. Find Sin Ѳ = 0. Find Cos Ѳ = .7. Inverses of Trigonometric Functions. Arccosine relation – the inverse of y = cos x Arcsine relation – the inverse of y = sin x Arctangent relation – the inverse of y = tan x. y = sin x y = cos x y = tan x.

370 views • 28 slides

Lesson 12.2

Lesson 12.2. Matrix Multiplication. Row and Column Order. The rows in a matrix are usually indexed 1 to m from top to bottom. The columns are usually indexed 1 to n from left to right. Elements are indexed by row, then column. Scalar Multiplication of Matrices.

395 views • 22 slides

Lesson 9 – Problem Solving with Relative Motion

Lesson 9 – Problem Solving with Relative Motion. August 12, 2013. Learning Goals. The student will learn effective problem solving tactics in physics The student will be able to solve problems related to relative motion, by adding and subtracting vector quantities by using a variety of methods.

293 views • 11 slides

1.5 Solving Right Triangles

1.5 Solving Right Triangles. JMerrill, 2005 Revised 2009. Recall from Last Week. SOH-CAH-TOA Sine: abbreviation: s in = Cosine: abbreviation: c os = Tangent: abbreviation: t an = These are the ratios of 2 sides. . Evaluating with a Calculator When .

242 views • 12 slides

8.3 Solving Right Triangles

8.3 Solving Right Triangles. Examples:. Use the trigonometric ratio to determine which angle of the triangle is  A. Examples:. Use the given trigonometric ratio to determine which angle of the triangle is  A. Examples:.

300 views • 10 slides

Solving Right Triangles. How do you solve right triangles?. M2 Unit 2: Day 6. To solve a right triangle you need…. Every right triangle has one right angle, two acute angles, one hypotenuse, and two legs. To SOLVE A RIGHT TRIANGLE means to find all 6 parts.

390 views • 16 slides

GEOMETRY Solving Right Triangles

GEOMETRY Solving Right Triangles. Warm Up. Use your calculator to find each trigonometric ratio. Round to the nearest hundredth. 1) sin 63˚ 2) cos 27˚ 3) tan 64˚. Right Triangles. You can use trigonometric ratios to change a percent grade to an angle measure.

453 views • 31 slides

Solving Right Triangles. Section 3.3. N. Solve a Right Triangle. The Tunnel of Samos. An island has a spring at point S , on one side of a mountain, M. A city at point C , on the other side of the mountain, needs the water.

316 views • 14 slides

2.5 Solving Right Triangles

2.5 Solving Right Triangles. OBJ: Find missing sides and angles of a right triangle. sin(74  8  14 ) sin(74 + 8 60 + 14 3600) = .962 74.137  sin (74.137  ). sin 0 0 sin 30 .5 sin 60 .87 sin 90 1

312 views • 12 slides

5-5: Solving Right Triangles

Alexis Mathis Aaron Goode Jessica Anderson. 5-5: Solving Right Triangles. Unit Circle. Pythagorean theorem. a²+b²=c² Used to determine the sides of a right triangle. Unit chart. Soh - Cah -Toa. Right triangle basics. Internal angle=180 Right angle=90

326 views • 16 slides

5.5 Solving Right Triangles

5.5 Solving Right Triangles. How do we find missing angle measurements? How do we evaluate inverse trig functions?. If I told you what could be? If I told you what could be? If I told you what could be? We can do this without the table too.

224 views • 11 slides

Solving right triangles

Solving right triangles. Warm Up Use ∆ ABC for Exercises 1–3. 1. If a = 8 and b = 5, find c . 2. If a = 60 and c = 61, find b . 3. If b = 6 and c = 10, find sin B . Find AB. 4. A (8, 10), B (3, 0) 5. A (1, –2), B (2, 6). 11. 0.6. Objective.

391 views • 26 slides

9.6 Solving Right Triangles. Objectives/Assignment. Solve a right triangle Use right triangles to solve problems Assignment: 2-36 even, 48-64 even. Solving a right triangle.

221 views • 14 slides

Chapter 12 - Lesson 12.2 Problem Solving with Right Triangles. HW: 12.2/1-20. Finding the Sides of a Triangle. Remember: SOHCAHTOA. Review: Trig Ratios. First we will find the Sine, Cosine and Tangent ratios for Angle P. P.

772 views • 38 slides

SOLVING RIGHT TRIANGLES

SOLVING RIGHT TRIANGLES. We will be given information about a triangle and then have to find the remaining sides and angles. We will develop new ways to find the area of triangles. We will apply the law of sines and law of cosines. SOH CAH TOA. PYTHAGOREAN THEOREM. SOH CAH TOA. B.

404 views • 10 slides

189 views • 16 slides

Chapter 12 12.1-12.2

Chapter 12 12.1-12.2. Geology and nonrenewable minerals Matt Healy. Case Study: The General Mining Law of 1872. Designed to encourage mineral exploration and the mining of hard rock minerals (gold, silver, zinc, etc) on US public lands and help to develop the then sparsely populated West.

386 views • 38 slides

Solving Right Triangles. How do you solve right triangles?. Day 53. Lesson 5.4. Sunday, January 5, 2020. Every right triangle has one right angle, two acute angles, one hypotenuse, and two legs. To SOLVE A RIGHT TRIANGLE means to find all 6 parts. Find the measure of the missing angle.

301 views • 26 slides