4.8 ideal gas law assignment

Ideal Gas Law Calculator

What is an ideal gas, ideal gas law equation, ideal gas constant.

This ideal gas law calculator will help you establish the properties of an ideal gas subject to pressure, temperature, or volume changes . Read on to learn about the characteristics of an ideal gas, how to use the ideal gas law equation, and the definition of the ideal gas constant.

We also recommend checking out our combined gas law calculator for further understanding of the basic thermodynamic processes of ideal gases.

An ideal gas is a special case of any gas that fulfills the following conditions:

The gas consists of a large number of molecules that move around randomly.

All molecules are point particles (they don't take up any space).

The molecules don't interact except for colliding.

All collisions between the particles of the gas are perfectly elastic (visit our conservation of momentum calculator to learn more).

The particles obey Newton's laws of motion.

The properties of an ideal gas are all summarized in one formula of the form:

• p p p – Pressure of the gas, measured in Pa;
• V V V – Volume of the gas, measured in m³;
• n n n – Amount of substance, measured in moles ;
• R R R – Ideal gas constant; and
• T T T – Temperature of the gas, measured in kelvins.

To find any of these values, simply enter the other ones into the ideal gas law calculator.

For example, if you want to calculate the volume of 40 moles of a gas under a pressure of 1013 hPa and at a temperature of 250 K, the result will be equal to:

V = nRT/p = 40 × 8.31446261815324 × 250 / 101300 = 0.82 m³ .

The gas constant (symbol R) is also called the molar or universal constant. It is used in many fundamental equations, such as the ideal gas law.

The value of this constant is 8.31446261815324 J/(mol·K) .

The gas constant is often defined as the product of Boltzmann's constant k (which relates the kinetic energy and temperature of a gas) and Avogadro's number (the number of atoms in a mole of substance):

You might find this air pressure at altitude calculator useful, too.

When can I use the ideal gas law?

You can apply the ideal gas law for every gas at a density low enough to prevent the emergence of strong intermolecular forces. In these conditions, every gas is more or less correctly modeled by the simple equation PV = nRT , which relates pressure, temperature, and volume.

What is the formula of the ideal gas law?

The formula of the ideal gas law is:

• P — Pressure , in pascal;
• V — Volume in cubic meters;
• n — Number of moles ;
• T — Temperature in kelvin; and
• R — Ideal gas constant .

Remember to use consistent units! The value commonly used for R , 8.314... J/mol·K refers to the pressure measured exclusively in pascals.

What is the pressure of 0.1 moles of a gas at 50 °C in a cubic meter?

268.7 Pa , or 0.00265 atm . To find this result:

Convert the temperature into kelvin:

T [K] = 273.15 + 50 = 323.15 K .

Compute the product of temperature, the number of moles, and the gas constant: nRT = 0.1 mol × 323.15 K × 8.3145 J/mol·K = 268.7 J (that is, energy ).

Divide by the volume. In this case, the volume is 1 , hence:

P = 268.7 Pa .

What are the three thermodynamics laws that can be identified in the ideal gas law?

The ideal gas law has four parameters . One of them is the number of moles which is a bit outside the scope of thermodynamics. The other three are pressure, temperature, and volume . We can identify three laws by fixing, in turn, each one of the three:

• Fixing the temperature, we find the isothermal transformation (or Boyle's law ): PV = k .
• Fixing the volume, we find the isochoric transformation ( Charles's law ): P/T = k .
• Fixing the pressure, we have the isobaric transformation ( Gay-Lussac's law ): V/T = k .

How do I calculate the temperature of a gas given moles, volume and pressure?

To calculate the temperature of a gas given the pressure and the volume, follow these simple steps:

Calculate the product of pressure and volumes. Be sure you're using consistent units: a good choice is pascals and cubic meters .

Calculate the product of the number of moles and the gas constant . If you used pascals and cubic meters, the constant is R = 8.3145 J/mol·K .

Divide the result of step 1 by the result of step 2: the result is the temperature (in kelvin ): T = PV/nR

Centripetal force

Crawl ratio, significant figures.

• Biology (100)
• Chemistry (100)
• Construction (144)
• Conversion (295)
• Ecology (30)
• Everyday life (262)
• Finance (570)
• Health (440)
• Physics (510)
• Sports (105)
• Statistics (182)
• Other (182)
• Discover Omni (40)

Want to create or adapt books like this? Learn more about how Pressbooks supports open publishing practices.

13 Temperature, Kinetic Theory, and the Gas Laws

95 13.3 The Ideal Gas Law

• State the ideal gas law in terms of molecules and in terms of moles.
• Use the ideal gas law to calculate pressure change, temperature change, volume change, or the number of molecules or moles in a given volume.
• Use Avogadro’s number to convert between number of molecules and number of moles.

In this section, we continue to explore the thermal behavior of gases. In particular, we examine the characteristics of atoms and molecules that compose gases. (Most gases, for example nitrogen,[latex]\boldsymbol{N_2},[/latex]and oxygen,[latex]\boldsymbol{O_2},[/latex]are composed of two or more atoms. We will primarily use the term “molecule” in discussing a gas because the term can also be applied to monatomic gases, such as helium.)

Gases are easily compressed. We can see evidence of this in [link] , where you will note that gases have the largest coefficients of volume expansion. The large coefficients mean that gases expand and contract very rapidly with temperature changes. In addition, you will note that most gases expand at the same rate, or have the same[latex]\beta.[/latex]This raises the question as to why gases should all act in nearly the same way, when liquids and solids have widely varying expansion rates.

The answer lies in the large separation of atoms and molecules in gases, compared to their sizes, as illustrated in Figure 2 . Because atoms and molecules have large separations, forces between them can be ignored, except when they collide with each other during collisions. The motion of atoms and molecules (at temperatures well above the boiling temperature) is fast, such that the gas occupies all of the accessible volume and the expansion of gases is rapid. In contrast, in liquids and solids, atoms and molecules are closer together and are quite sensitive to the forces between them.

To get some idea of how pressure, temperature, and volume of a gas are related to one another, consider what happens when you pump air into an initially deflated tire. The tire’s volume first increases in direct proportion to the amount of air injected, without much increase in the tire pressure. Once the tire has expanded to nearly its full size, the walls limit volume expansion. If we continue to pump air into it, the pressure increases. The pressure will further increase when the car is driven and the tires move. Most manufacturers specify optimal tire pressure for cold tires. (See Figure 3 .)

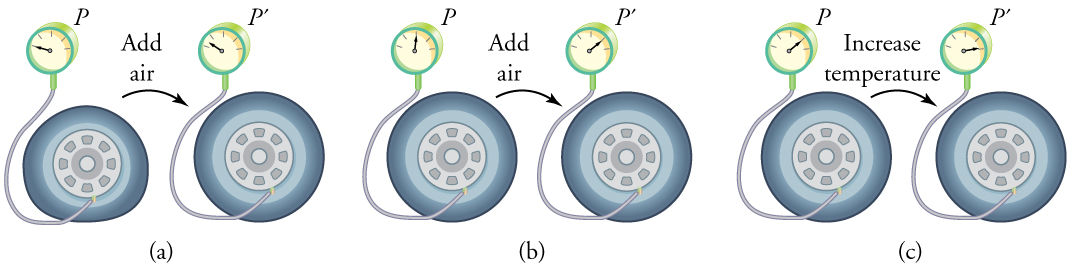
At room temperatures, collisions between atoms and molecules can be ignored. In this case, the gas is called an ideal gas, in which case the relationship between the pressure, volume, and temperature is given by the equation of state called the ideal gas law.

IDEAL GAS LAW

The ideal gas law states that

where[latex]\boldsymbol{P}[/latex]is the absolute pressure of a gas,[latex]\boldsymbol{V}[/latex]is the volume it occupies,[latex]\boldsymbol{N}[/latex]is the number of atoms and molecules in the gas, and[latex]\boldsymbol{T}[/latex]is its absolute temperature. The constant[latex]\boldsymbol{k}[/latex]is called the Boltzmann constant in honor of Austrian physicist Ludwig Boltzmann (1844–1906) and has the value

The ideal gas law can be derived from basic principles, but was originally deduced from experimental measurements of Charles’ law (that volume occupied by a gas is proportional to temperature at a fixed pressure) and from Boyle’s law (that for a fixed temperature, the product[latex]\boldsymbol{PV}[/latex]is a constant). In the ideal gas model, the volume occupied by its atoms and molecules is a negligible fraction of[latex]\boldsymbol{V}.[/latex]The ideal gas law describes the behavior of real gases under most conditions. (Note, for example, that[latex]\boldsymbol{N}[/latex]is the total number of atoms and molecules, independent of the type of gas.)

Let us see how the ideal gas law is consistent with the behavior of filling the tire when it is pumped slowly and the temperature is constant. At first, the pressure[latex]\boldsymbol{P}[/latex]is essentially equal to atmospheric pressure, and the volume[latex]\boldsymbol{V}[/latex]increases in direct proportion to the number of atoms and molecules[latex]\boldsymbol{N}[/latex]put into the tire. Once the volume of the tire is constant, the equation[latex]\boldsymbol{PV=NkT}[/latex]predicts that the pressure should increase in proportion to the number N of atoms and molecules .

Example 1: Calculating Pressure Changes Due to Temperature Changes: Tire Pressure

Suppose your bicycle tire is fully inflated, with an absolute pressure of[latex]\boldsymbol{7.00\times10^5\textbf{ Pa}}[/latex](a gauge pressure of just under[latex]\boldsymbol{90.0\textbf{ lb/in}^2}[/latex]) at a temperature of[latex]\boldsymbol{18.0^0\textbf{C}}.[/latex]What is the pressure after its temperature has risen to[latex]\boldsymbol{35.0^0\textbf{C}}?[/latex]Assume that there are no appreciable leaks or changes in volume.

The pressure in the tire is changing only because of changes in temperature. First we need to identify what we know and what we want to know, and then identify an equation to solve for the unknown.

We know the initial pressure[latex]\boldsymbol{P_0=7.00\times10^5\textbf{ Pa}},[/latex]the initial temperature[latex]\boldsymbol{T_0=18.0^0\textbf{C}},[/latex]and the final temperature[latex]\boldsymbol{T_{\textbf{f}}=35.0^0\textbf{C}}.[/latex]We must find the final pressure[latex]\boldsymbol{P_{\textbf{f}}}.[/latex]How can we use the equation[latex]\boldsymbol{PV=NkT}?[/latex]At first, it may seem that not enough information is given, because the volume[latex]\boldsymbol{V}[/latex]and number of atoms[latex]\boldsymbol{N}[/latex]are not specified. What we can do is use the equation twice:[latex]\boldsymbol{P_0V_0=NkT_0}[/latex]and[latex]\boldsymbol{P_{\textbf{f}}V_{\textbf{f}}=NkT_{\textbf{f}}}.[/latex]If we divide[latex]\boldsymbol{P_{\textbf{f}}V_{\textbf{f}}}[/latex]by[latex]\boldsymbol{P_0V_0}[/latex]we can come up with an equation that allows us to solve for[latex]\boldsymbol{P_{\textbf{f}}}.[/latex]

Since the volume is constant,[latex]\boldsymbol{V_{\textbf{f}}}[/latex]and[latex]\boldsymbol{V_0}[/latex]are the same and they cancel out. The same is true for[latex]\boldsymbol{N_{\textbf{f}}}[/latex]and[latex]\boldsymbol{N_0},[/latex]and[latex]\boldsymbol{k},[/latex]which is a constant. Therefore,

We can then rearrange this to solve for[latex]\boldsymbol{P_{\textbf{f}}}:[/latex]

where the temperature must be in units of kelvins, because[latex]\boldsymbol{T_0}[/latex]and[latex]\boldsymbol{T_{\textbf{f}}}[/latex]are absolute temperatures.

1. Convert temperatures from Celsius to Kelvin.

2. Substitute the known values into the equation.

The final temperature is about 6% greater than the original temperature, so the final pressure is about 6% greater as well. Note that absolute pressure and absolute temperature must be used in the ideal gas law.

MAKING CONNECTIONS: TAKE-HOME EXPERIMENT—REFRIGERATING A BALLOON

Inflate a balloon at room temperature. Leave the inflated balloon in the refrigerator overnight. What happens to the balloon, and why?

Example 2: Calculating the Number of Molecules in a Cubic Meter of Gas

How many molecules are in a typical object, such as gas in a tire or water in a drink? We can use the ideal gas law to give us an idea of how large[latex]\boldsymbol{N}[/latex]typically is.

Calculate the number of molecules in a cubic meter of gas at standard temperature and pressure (STP), which is defined to be[latex]\boldsymbol{0^0\textbf{C}}[/latex]and atmospheric pressure.

Because pressure, volume, and temperature are all specified, we can use the ideal gas law[latex]\boldsymbol{PV=NkT},[/latex]to find[latex]\boldsymbol{N}.[/latex]

1. Identify the knowns.

2. Identify the unknown: number of molecules,[latex]\boldsymbol{N}.[/latex]

3. Rearrange the ideal gas law to solve for[latex]\boldsymbol{N}.[/latex]

4. Substitute the known values into the equation and solve for[latex]\boldsymbol{N}.[/latex]

This number is undeniably large, considering that a gas is mostly empty space.[latex]\boldsymbol{N}[/latex]is huge, even in small volumes. For example,[latex]\boldsymbol{1\textbf{ cm}^3}[/latex]of a gas at STP has[latex]\boldsymbol{2.68\times10^{19}}[/latex]molecules in it. Once again, note that[latex]\boldsymbol{N}[/latex]is the same for all types or mixtures of gases.

Moles and Avogadro’s Number

It is sometimes convenient to work with a unit other than molecules when measuring the amount of substance. A mole (abbreviated mol) is defined to be the amount of a substance that contains as many atoms or molecules as there are atoms in exactly 12 grams (0.012 kg) of carbon-12. The actual number of atoms or molecules in one mole is called Avogadro’s number [latex]\boldsymbol{(N_{\textbf{A}})},[/latex]in recognition of Italian scientist Amedeo Avogadro (1776–1856). He developed the concept of the mole, based on the hypothesis that equal volumes of gas, at the same pressure and temperature, contain equal numbers of molecules. That is, the number is independent of the type of gas. This hypothesis has been confirmed, and the value of Avogadro’s number is

AVOGADRO’S NUMBER

One mole always contains[latex]\boldsymbol{6.02\times10^{23}}[/latex]particles (atoms or molecules), independent of the element or substance. A mole of any substance has a mass in grams equal to its molecular mass, which can be calculated from the atomic masses given in the periodic table of elements.

Check Your Understanding 1

The active ingredient in a Tylenol pill is 325 mg of acetaminophen[latex]\boldsymbol{(\textbf{C}_8\textbf{H}_9\textbf{NO}_2)}.[/latex]Find the number of active molecules of acetaminophen in a single pill.

Example 3: Calculating Moles per Cubic Meter and Liters per Mole

Calculate: (a) the number of moles in[latex]\boldsymbol{1.00\textbf{ m}^3}[/latex]of gas at STP, and (b) the number of liters of gas per mole.

Strategy and Solution

(a) We are asked to find the number of moles per cubic meter, and we know from Example 2 that the number of molecules per cubic meter at STP is[latex]\boldsymbol{2.68\times10^{25}}.[/latex]The number of moles can be found by dividing the number of molecules by Avogadro’s number. We let[latex]\boldsymbol{n}[/latex]stand for the number of moles,

(b) Using the value obtained for the number of moles in a cubic meter, and converting cubic meters to liters, we obtain

This value is very close to the accepted value of 22.4 L/mol. The slight difference is due to rounding errors caused by using three-digit input. Again this number is the same for all gases. In other words, it is independent of the gas.

The (average) molar weight of air (approximately 80%[latex]\boldsymbol{\textbf{N}_2}[/latex]and 20%[latex]\boldsymbol{\textbf{O}_2}[/latex]is[latex]\boldsymbol{M=28.8\textbf{ g}}.[/latex]Thus the mass of one cubic meter of air is 1.28 kg. If a living room has dimensions[latex]\boldsymbol{5\textbf{ m}\times5\textbf{ m}\times3\textbf{ m}},[/latex]the mass of air inside the room is 96 kg, which is the typical mass of a human.

Check Your Understanding 2

The density of air at standard conditions[latex]\boldsymbol{(P=1\textbf{ atm }}[/latex]and[latex]\boldsymbol{T=20^0\textbf{C})}[/latex]is[latex]\boldsymbol{1.28\textbf{ kg/m}^3}.[/latex]At what pressure is the density[latex]\boldsymbol{0.64\textbf{ kg/m}^3}[/latex]if the temperature and number of molecules are kept constant?

The Ideal Gas Law Restated Using Moles

A very common expression of the ideal gas law uses the number of moles,[latex]\boldsymbol{n},[/latex]rather than the number of atoms and molecules,[latex]\boldsymbol{N}.[/latex]We start from the ideal gas law,

and multiply and divide the equation by Avogadro’s number[latex]\boldsymbol{N_{\textbf{A}}}.[/latex]This gives

Note that[latex]\boldsymbol{n=N/N_{\textbf{A}}}[/latex]is the number of moles. We define the universal gas constant[latex]\boldsymbol{R=N_{\textbf{A}}k},[/latex]and obtain the ideal gas law in terms of moles.

IDEAL GAS LAW (IN TERMS OF MOLES)

The ideal gas law (in terms of moles) is

The numerical value of[latex]\boldsymbol{R}[/latex]in SI units is

In other units,

You can use whichever value of[latex]\boldsymbol{R}[/latex]is most convenient for a particular problem.

Example 4: Calculating Number of Moles: Gas in a Bike Tire

How many moles of gas are in a bike tire with a volume of[latex]\boldsymbol{2.00\times10^{-3}\textbf{ m}^3\:(2.00\textbf{ L})}[/latex]a pressure of[latex]\boldsymbol{7.00\times10^5\textbf{ Pa}}[/latex](a gauge pressure of just under[latex]\boldsymbol{90.0\textbf{ lb/in}^2}[/latex]), and at a temperature of[latex]\boldsymbol{18.0^0\textbf{C}}?[/latex]

Identify the knowns and unknowns, and choose an equation to solve for the unknown. In this case, we solve the ideal gas law,[latex]\boldsymbol{PV=nRT},[/latex]for the number of moles[latex]\boldsymbol{n}.[/latex]

2. Rearrange the equation to solve for[latex]\boldsymbol{n}[/latex]and substitute known values.

The most convenient choice for[latex]\boldsymbol{R}[/latex]in this case is[latex]\boldsymbol{8.31\textbf{ J/mol}\cdotp\textbf{K}},[/latex]because our known quantities are in SI units. The pressure and temperature are obtained from the initial conditions in Example 1 , but we would get the same answer if we used the final values.

The ideal gas law can be considered to be another manifestation of the law of conservation of energy (see Chapter 7.6 Conservation of Energy ). Work done on a gas results in an increase in its energy, increasing pressure and/or temperature, or decreasing volume. This increased energy can also be viewed as increased internal kinetic energy, given the gas’s atoms and molecules.

The Ideal Gas Law and Energy

Let us now examine the role of energy in the behavior of gases. When you inflate a bike tire by hand, you do work by repeatedly exerting a force through a distance. This energy goes into increasing the pressure of air inside the tire and increasing the temperature of the pump and the air.

The ideal gas law is closely related to energy: the units on both sides are joules. The right-hand side of the ideal gas law in[latex]\boldsymbol{PV=NkT}[/latex]is[latex]\boldsymbol{NkT}.[/latex]This term is roughly the amount of translational kinetic energy of[latex]\boldsymbol{N}[/latex]atoms or molecules at an absolute temperature[latex]\boldsymbol{T},[/latex]as we shall see formally in Chapter 13.4 Kinetic Theory: Atomic and Molecular Explanation of Pressure and Temperature . The left-hand side of the ideal gas law is[latex]\boldsymbol{PV},[/latex]which also has the units of joules. We know from our study of fluids that pressure is one type of potential energy per unit volume, so pressure multiplied by volume is energy. The important point is that there is energy in a gas related to both its pressure and its volume. The energy can be changed when the gas is doing work as it expands—something we explore in Chapter 14 Heat and Heat Transfer Methods —similar to what occurs in gasoline or steam engines and turbines.

PROBLEM-SOLVING STRATEGY: THE IDEAL GAS LAW

Step 1 Examine the situation to determine that an ideal gas is involved. Most gases are nearly ideal.

Step 2 Make a list of what quantities are given, or can be inferred from the problem as stated (identify the known quantities). Convert known values into proper SI units (K for temperature, Pa for pressure,[latex]\boldsymbol{\textbf{m}^3}[/latex]for volume, molecules for[latex]\boldsymbol{N},[/latex]and moles for[latex]\boldsymbol{n}[/latex]).

Step 3 Identify exactly what needs to be determined in the problem (identify the unknown quantities). A written list is useful.

Step 4 Determine whether the number of molecules or the number of moles is known, in order to decide which form of the ideal gas law to use. The first form is[latex]\boldsymbol{PV=NkT}[/latex]and involves[latex]\boldsymbol{N},[/latex]the number of atoms or molecules. The second form is[latex]\boldsymbol{PV=nRT}[/latex]and involves[latex]\boldsymbol{n},[/latex]the number of moles.

Step 5 Solve the ideal gas law for the quantity to be determined (the unknown quantity). You may need to take a ratio of final states to initial states to eliminate the unknown quantities that are kept fixed.

Step 6 Substitute the known quantities, along with their units, into the appropriate equation, and obtain numerical solutions complete with units. Be certain to use absolute temperature and absolute pressure.

Step 7 Check the answer to see if it is reasonable: Does it make sense?

Check Your Understanding 3

Liquids and solids have densities about 1000 times greater than gases. Explain how this implies that the distances between atoms and molecules in gases are about 10 times greater than the size of their atoms and molecules.

Section Summary

• The ideal gas law relates the pressure and volume of a gas to the number of gas molecules and the temperature of the gas.

where[latex]\boldsymbol{P}[/latex]is pressure,[latex]\boldsymbol{V}[/latex]is volume,[latex]\boldsymbol{T}[/latex]is temperature,[latex]\boldsymbol{N}[/latex]is number of molecules, and[latex]\boldsymbol{k}[/latex]is the Boltzmann constant

• A mole is the number of atoms in a 12-g sample of carbon-12.
• The number of molecules in a mole is called Avogadro’s number[latex]\boldsymbol{N_{\textbf{A}}},[/latex] [latex]\boldsymbol{N_{\textbf{A}}=6.02\times10^{23}\textbf{ mol}^{-1}}.[/latex]
• A mole of any substance has a mass in grams equal to its molecular weight, which can be determined from the periodic table of elements.

where[latex]\boldsymbol{n}[/latex]is number of moles and[latex]\boldsymbol{R}[/latex]is the universal gas constant,

• The ideal gas law is generally valid at temperatures well above the boiling temperature.

Conceptual Questions

1: Find out the human population of Earth. Is there a mole of people inhabiting Earth? If the average mass of a person is 60 kg, calculate the mass of a mole of people. How does the mass of a mole of people compare with the mass of Earth?

2: Under what circumstances would you expect a gas to behave significantly differently than predicted by the ideal gas law?

3: A constant-volume gas thermometer contains a fixed amount of gas. What property of the gas is measured to indicate its temperature?

Problems & Exercises

1: The gauge pressure in your car tires is[latex]\boldsymbol{2.50\times10^5\textbf{ N/m}^2}[/latex]at a temperature of[latex]\boldsymbol{35.0^0\textbf{C}}[/latex]when you drive it onto a ferry boat to Alaska. What is their gauge pressure later, when their temperature has dropped to[latex]\boldsymbol{-40.0^0\textbf{C}}?[/latex]

2: Convert an absolute pressure of[latex]\boldsymbol{7.00\times10^5\textbf{ N/m}^2}[/latex]to gauge pressure in[latex]\boldsymbol{\textbf{lb/in}^2}.[/latex](This value was stated to be just less than[latex]\boldsymbol{90.0\textbf{ lb/in}^2}[/latex]in Example 4 . Is it?)

3: Suppose a gas-filled incandescent light bulb is manufactured so that the gas inside the bulb is at atmospheric pressure when the bulb has a temperature of[latex]\boldsymbol{20.0^0\textbf{C}}.[/latex](a) Find the gauge pressure inside such a bulb when it is hot, assuming its average temperature is[latex]\boldsymbol{60.0^0\textbf{C}}[/latex](an approximation) and neglecting any change in volume due to thermal expansion or gas leaks. (b) The actual final pressure for the light bulb will be less than calculated in part (a) because the glass bulb will expand. What will the actual final pressure be, taking this into account? Is this a negligible difference?

4: Large helium-filled balloons are used to lift scientific equipment to high altitudes. (a) What is the pressure inside such a balloon if it starts out at sea level with a temperature of[latex]\boldsymbol{10.0^0\textbf{C}}[/latex]and rises to an altitude where its volume is twenty times the original volume and its temperature is[latex]\boldsymbol{-50.0^0\textbf{C}}?[/latex](b) What is the gauge pressure? (Assume atmospheric pressure is constant.)

5: Confirm that the units of[latex]\boldsymbol{nRT}[/latex]are those of energy for each value of[latex]\boldsymbol{R}:[/latex](a)[latex]\boldsymbol{8.31\textbf{ J/mol}\cdotp\textbf{K}},[/latex](b)[latex]\boldsymbol{1.99\textbf{ cal/mol}\cdotp\textbf{K}},[/latex]and (c)[latex]\boldsymbol{0.0821\textbf{ L}\cdotp\textbf{atm/mol}\cdotp\textbf{K}}.[/latex]

6: In the text, it was shown that[latex]\boldsymbol{N/V=2.68\times10^{25}\textbf{ m}^{-3}}[/latex]for gas at STP. (a) Show that this quantity is equivalent to[latex]\boldsymbol{N/V=2.68\times10^{19}\textbf{ cm}^{-3}},[/latex]as stated. (b) About how many atoms are there in one[latex]\boldsymbol{\mu\textbf{m}^3}[/latex](a cubic micrometer) at STP? (c) What does your answer to part (b) imply about the separation of atoms and molecules?

7: Calculate the number of moles in the 2.00-L volume of air in the lungs of the average person. Note that the air is at[latex]\boldsymbol{37.0^0\textbf{C}}[/latex](body temperature).

8: An airplane passenger has[latex]\boldsymbol{100\textbf{ cm}^3}[/latex]of air in his stomach just before the plane takes off from a sea-level airport. What volume will the air have at cruising altitude if cabin pressure drops to[latex]\boldsymbol{7.50\times10^4\textbf{ N/m}^2}?[/latex]

9: (a) What is the volume (in[latex]\boldsymbol{\textbf{km}^3}[/latex]) of Avogadro’s number of sand grains if each grain is a cube and has sides that are 1.0 mm long? (b) How many kilometers of beaches in length would this cover if the beach averages 100 m in width and 10.0 m in depth? Neglect air spaces between grains.

10: An expensive vacuum system can achieve a pressure as low as[latex]\boldsymbol{1.00\times10^{-7}\textbf{ N/m}^2}[/latex]at[latex]\boldsymbol{20^0\textbf{C}}.[/latex]How many atoms are there in a cubic centimeter at this pressure and temperature?

11: The number density of gas atoms at a certain location in the space above our planet is about[latex]\boldsymbol{1.00\times10^{11}\textbf{ m}^{-3}},[/latex]and the pressure is[latex]\boldsymbol{2.75\times10^{-10}\textbf{ N/m}^2}[/latex]in this space. What is the temperature there?

12: A bicycle tire has a pressure of[latex]\boldsymbol{7.00\times10^5\textbf{ N/m}^2}[/latex]at a temperature of[latex]\boldsymbol{18.0^0\textbf{C}}[/latex]and contains 2.00 L of gas. What will its pressure be if you let out an amount of air that has a volume of[latex]\boldsymbol{100\textbf{ cm}^3}[/latex]at atmospheric pressure? Assume tire temperature and volume remain constant.

13: A high-pressure gas cylinder contains 50.0 L of toxic gas at a pressure of[latex]\boldsymbol{1.40\times10^7\textbf{ N/m}^2}[/latex]and a temperature of[latex]\boldsymbol{25.0^0\textbf{C}}.[/latex]Its valve leaks after the cylinder is dropped. The cylinder is cooled to dry ice temperature[latex]\boldsymbol{(-78.5^0\textbf{C})}[/latex]to reduce the leak rate and pressure so that it can be safely repaired. (a) What is the final pressure in the tank, assuming a negligible amount of gas leaks while being cooled and that there is no phase change? (b) What is the final pressure if one-tenth of the gas escapes? (c) To what temperature must the tank be cooled to reduce the pressure to 1.00 atm (assuming the gas does not change phase and that there is no leakage during cooling)? (d) Does cooling the tank appear to be a practical solution?

14: Find the number of moles in 2.00 L of gas at[latex]\boldsymbol{35.0^0\textbf{C}}[/latex]and under[latex]\boldsymbol{7.41\times10^7\textbf{ N/m}^2}[/latex]of pressure.

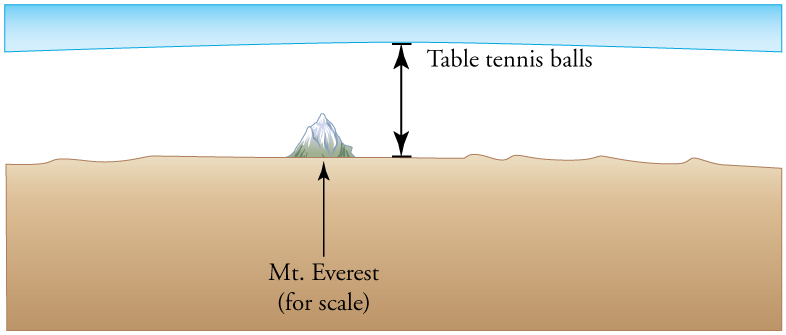
15: Calculate the depth to which Avogadro’s number of table tennis balls would cover Earth. Each ball has a diameter of 3.75 cm. Assume the space between balls adds an extra 25.0% to their volume and assume they are not crushed by their own weight.

16: (a) What is the gauge pressure in a[latex]\boldsymbol{25.0^0\textbf{C}}[/latex]car tire containing 3.60 mol of gas in a 30.0 L volume? (b) What will its gauge pressure be if you add 1.00 L of gas originally at atmospheric pressure and[latex]\boldsymbol{25.0^0\textbf{C}}?[/latex]Assume the temperature returns to[latex]\boldsymbol{25.0^0\textbf{C}}[/latex]and the volume remains constant.

17: (a) In the deep space between galaxies, the density of atoms is as low as[latex]\boldsymbol{10^6\textbf{ atoms/m}^3},[/latex]and the temperature is a frigid 2.7 K. What is the pressure? (b) What volume (in[latex]\boldsymbol{\textbf{m}^3}[/latex]) is occupied by 1 mol of gas? (c) If this volume is a cube, what is the length of its sides in kilometers?

We first need to calculate the molar mass (the mass of one mole) of acetaminophen. To do this, we need to multiply the number of atoms of each element by the element’s atomic mass.

Then we need to calculate the number of moles in 325 mg.

Then use Avogadro’s number to calculate the number of molecules.

The best way to approach this question is to think about what is happening. If the density drops to half its original value and no molecules are lost, then the volume must double. If we look at the equation[latex]\boldsymbol{PV=NkT},[/latex]we see that when the temperature is constant, the pressure is inversely proportional to volume. Therefore, if the volume doubles, the pressure must drop to half its original value, and[latex]\boldsymbol{P_{\textbf{f}}=0.50\textbf{ atm}}.[/latex]

Atoms and molecules are close together in solids and liquids. In gases they are separated by empty space. Thus gases have lower densities than liquids and solids. Density is mass per unit volume, and volume is related to the size of a body (such as a sphere) cubed. So if the distance between atoms and molecules increases by a factor of 10, then the volume occupied increases by a factor of 1000, and the density decreases by a factor of 1000.

(a) 0.136 atm

(b) 0.135 atm. The difference between this value and the value from part (a) is negligible.

(a)[latex]\boldsymbol{nRT=(\textbf{mol})(\textbf{J/mol}\cdotp\textbf{K})(\textbf{K})=\textbf{ J}}[/latex]

(b)[latex]\boldsymbol{nRT=(\textbf{mol})(\textbf{cal/mol}\cdotp\textbf{K})(\textbf{K})=\textbf{ cal}}[/latex]

(c)[latex]\begin{array}{ll} \boldsymbol{nRT} & \boldsymbol{=(\textbf{mol})(\textbf{L}\cdotp\textbf{atm/mol}\cdotp\textbf{K})(\textbf{K})} \\ {} & \boldsymbol{=\textbf{ L}\cdotp\textbf{atm}=(\textbf{m}^3)(\textbf{N/m}^2)} \\ {} & \boldsymbol{=\textbf{N}\cdotp\textbf{m}=\textbf{J}} \end{array}[/latex]

[latex]\boldsymbol{7.86\times10^{-2}\textbf{ mol}}[/latex]

(a)[latex]\boldsymbol{6.02\times10^5\textbf{ km}^3}[/latex]

(b)[latex]\boldsymbol{6.02\times10^8\textbf{ km}}[/latex]

[latex]\boldsymbol{-73.9^0\textbf{C}}[/latex]

(a)[latex]\boldsymbol{9.14\times10^6\textbf{ N/m}^2}[/latex]

(b)[latex]\boldsymbol{8.23\times10^6\textbf{ N/m}^2}[/latex]

(d) No. The final temperature needed is much too low to be easily achieved for a large object.

(a)[latex]\boldsymbol{3.7\times10^{-17}\textbf{ Pa}}[/latex]

(b)[latex]\boldsymbol{6.0\times10^{17}\textbf{ m}^3}[/latex]

(c)[latex]\boldsymbol{8.4\times10^2\textbf{ km}}[/latex]

College Physics chapters 1-17 Copyright © August 22, 2016 by OpenStax is licensed under a Creative Commons Attribution 4.0 International License , except where otherwise noted.

Share This Book

Ideal Gas Law Calculator

Enter the values of volume (V), number of moles (n) and absolute temperature (T) below which you want to find the pressure of an ideal gas.

The Ideal Gas Law calculator finds the pressure of an ideal gas using the given values.

The Ideal Gas Law is given by

P V = n R T P = Pressure V = Volume n = Number of moles R = Ideal gas constant T = Absolute temperature

Click the blue arrow to submit. Choose "Find the Pressure" from the topic selector and click to see the result in our Physics Calculator!

Find the Pressure

Please ensure that your password is at least 8 characters and contains each of the following:

• a special character: @$#!%*?&

R is called the gas constant. It was first discovered, as part of the discovery in the mid-1830's by Emil Clapeyron of what is now called the Ideal Gas Law. Sometimes it is called the universal constant because it shows up in many non-gas-related situations. However, it is mostly called the gas constant or, sometimes, the universal gas constant. Depending on the units selected, the "value" for R can take on many different forms. Here is a list. Keep in mind these different "values" represent the same thing.

V = nRT / P

V = [(2.34 g / 44.0 g mol¯ 1 ) (0.08206 L atm mol¯ 1 K¯ 1 ) (273.0 K)] / 1.00 atm V = 1.19 L (to three significant figures)

n = PV / RT

n = [(1.00 atm) (56.2 L) ] / [ (0.08206 L atm mol¯ 1 K¯ 1 ) (273.0 K)] n = 2.50866 mol (I'll keep a few guard digits)

2.50866 mol times 39.948 g/mol = 100. g (to three sig figs)

T = PV / nR

T = [(1.95 atm) (12.30 L)] / [(0.654 mol) (0.08206 L atm mol¯ 1 K¯ 1 )] T = 447 K

Since one mole of gas occupies 22.414 L at STP, the molecular weight of the gas is 30.6 g mol¯ 1

11.2 L at STP is one-half molar volume, so there is 0.500 mol of gas present. Therefore, the molecular weight is 80.0 g mol¯ 1

(1.00 atm) (19.2 L) = (n) (0.08206) (273 K) n = 0.8570518 mol (I'll keep a few guard digits)

12.0 g / 0.8570518 mol = 14.0 g/mol

(19.2 L / 12.0 g) = (22.414 L / x ) 19.2x = 268.968 x = 14.0 g/mol

n = PV / RT n = [(700.0 mmHg / 760.0 mmHg atm¯ 1 ) (48.0 L)] / [(0.08206 L atm mol¯ 1 K¯ 1 ) (293.0 K)] n = 1.8388 mol

96.0 g / 1.8388 mol = 52.2 g/mol

n = PV / RT n = [(79.97 kPa / 101.325 kPa atm¯ 1 ) (4.167 L)] / [(0.08206 L atm mol¯ 1 K¯ 1 ) (303.0 K)] n = 0.13227 mol

20.83 g / 0.13227 mol = 157.5 g/mol

8.31451 J mol¯ 1 K¯ 1 / 0.0820574 L atm mol¯ 1 K¯ 1 = 101.3255 J L¯ 1 atm¯ 1 This means that 1 L atm = 101.3255 J

0.0820574/8.31451 = 0.00986918 (try putting the units in as was done just above) This means that 1 J = 0.00986918 L atm You could have also done this: 1 / 101.3255 = 0.00986918

(0.0820574 atm L/mol K) (101.3255 J/L atm) = 8.31451 J/mol K and (8.31451 J/mol K) (0.00986918 L atm / J) = 0.0820574 L atm / mol K

5.600 g / 44.009 g/mol = 0.1272467 mol

(P) (4.00 L) = (0.1272467 mol) (0.08206 L atm mol¯ 1 K¯ 1 ) (300 K) P = 0.7831 atm (to four sig figs)

Notice that we have pressure, volume and temperature explicitly mentioned. In addition, mass and molecular weight will give us moles. It appears that the ideal gas law is called for. However, there is a problem. We are being asked to change the conditions to a new amount of moles and pressure. So, it seems like the ideal gas law needs to be used twice.

P 1 V 1 = n 1 RT 1 This equation will use the 2.035 g amount of H 2 as well as the 1.015 atm, 5.00 L, and the -211.76 °C (converted to Kelvin, which I will do in a moment). P 2 V 2 = n 2 RT 2 This second equation will use the data in the second sentence and T 2 will be the unknown. What I need to do is set the two equations equal to each other. First, I rearrange a bit.

P 1 V 1 = n 1 RT 1 leads to:     P 1 V 1 R = –––––     n 1 T 1 and P 2 V 2 = n 2 RT 2 leads to:     P 2 V 2 R = –––––     n 2 T 2

R = R, therefore: P 1 V 1   P 2 V 2 ––––– = ––––– n 1 T 1   n 2 T 2

Since the volume never changes, we can eliminate it from the equation: P 1   P 2 ––––– = ––––– n 1 T 1   n 2 T 2

P 1 n 2 T 2 = P 2 n 1 T 1

    P 2 n 1 T 1 T 2 = –––––     P 1 n 2

T 2 = P 2 n 1 T 1 / P 1 n 2

Each of the mole amounts would be arrived at by dividing the grams by the molar mass (in this case, H 2 ). However, notice the molar masses will cancel, being the same numerical value and one in the nominator and one in the denominator. After cancelling, this is what we wind up with:     P 2 mass 1 T 1 T 2 = –––––––––     P 1 mass 2

    (3.015 atm) (2.035 g) (61.24 K) T 2 = –––––––––––––––––––––––––     (1.015 atm) (4.134 g) T 2 = 89.546867 K

°C = 89.546867 K − 273.15 (I decided to use 273.15 rather than 273.) Using four sig figs gives −183.6 °C for the final answer

(P) (22.414 L) = (2.00 mol) (0.08206 L atm / mol K) (T)

T/P = 22.414 L / [(2.00 mol) (0.08206 L atm / mol K)] T/P = 136.57 K/atm Any T/P combination that gives 136.57 will be an answer.

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons
• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

4.7: Ideal Gas Statistical Mechanics

• Last updated
• Save as PDF
• Page ID 18756

• Daniel Arovas
• UC San Diego

\( \newcommand\bes{\begin{equation}\begin{split}}\) \( \newcommand\ltwid{\propto}\) \( \newcommand\ees{\end{split}\end{equation}}\) \( \newcommand\mib{\mathbf}\) \( \newcommand\Sa{\textsf a}\) \( \newcommand\Sb{\textsf b}\) \( \newcommand\Sc{\textsf c}\) \( \newcommand\Sd{\textsf d}\) \( \newcommand\Se{\textsf e}\) \( \newcommand\Sf{\textsf f}\) \( \newcommand\Sg{\textsf g}\) \( \newcommand\Sh{\textsf h}\) \( \newcommand\Si{\textsf i}\) \( \newcommand\Sj{\textsf j}\) \( \newcommand\Sk{\textsf k}\) \( \newcommand\Sl{\textsf l}\) \( \newcommand\Sm{\textsf m}\) \( \newcommand\Sn{\textsf n}\) \( \newcommand\So{\textsf o}\) \( \newcommand\Sp{\textsf p}\) \( \newcommand\Sq{\textsf q}\) \( \newcommand\Sr{\textsf r}\) \( \newcommand\Ss{\textsf s}\) \( \newcommand\St{\textsf t}\) \( \newcommand\Su{\textsf u}\) \( \newcommand\Sv{\textsf v}\) \( \newcommand\Sw{\textsf w}\) \( \newcommand\Sx{\textsf x}\) \( \newcommand\Sy{\textsf y}\) \( \newcommand\Sz{\textsf z}\) \( \newcommand\SA{\textsf A}\) \( \newcommand\SB{\textsf B}\) \( \newcommand\SC{\textsf C}\) \( \newcommand\SD{\textsf D}\) \( \newcommand\SE{\textsf E}\) \( \newcommand\SF{\textsf F}\) \( \newcommand\SG{\textsf G}\) \( \newcommand\SH{\textsf H}\) \( \newcommand\SI{\textsf I}\) \( \newcommand\SJ{\textsf J}\) \( \newcommand\SK{\textsf K}\) \( \newcommand\SL{\textsf L}\) \( \newcommand\SM{\textsf M}\) \( \newcommand\SN{\textsf N}\) \( \newcommand\SO{\textsf O}\) \( \newcommand\SP{\textsf P}\) \( \newcommand\SQ{\textsf Q}\) \( \newcommand\SR{\textsf R}\) \( \newcommand\SS{\textsf S}\) \( \newcommand\ST{\textsf T}\) \( \newcommand\SU{\textsf U}\) \( \newcommand\SV{\textsf V}\) \( \newcommand\SW{\textsf W}\) \( \newcommand\SX{\textsf X}\) \( \newcommand\SY{\textsf Y}\) \( \newcommand\SZ{\textsf Z}\) \( \newcommand\Ha{\hat a}\) \( \newcommand\Hb{\hat b}\) \( \newcommand\Hc{\hat c}\) \( \newcommand\Hd{\hat d}\) \( \newcommand\He{\hat e}\) \( \newcommand\Hf{\hat f}\) \( \newcommand\Hg{\hat g}\) \( \newcommand\Hh{\hat h}\) \( \newcommand\Hi{\hat \imath}\) \( \newcommand\Hj{\hat \jmath}\) \( \newcommand\Hk{\hat k}\) \( \newcommand\Hl{\hat l}\) \( \newcommand\Hm{\hat m}\) \( \newcommand\Hn{\hat n}\) \( \newcommand\Ho{\hat o}\) \( \newcommand\Hp{\hat p}\) \( \newcommand\Hq{\hat q}\) \( \newcommand\Hr{\hat r}\) \( \newcommand\Hs{\hat s}\) \( \newcommand\Ht{\hat t}\) \( \newcommand\Hu{\hat u}\) \( \newcommand\Hv{\hat v}\) \( \newcommand\Hw{\hat w}\) \( \newcommand\Hx{\hat x}\) \( \newcommand\Hy{\hat y}\) \( \newcommand\Hz{\hat z}\) \( \newcommand\HA{\hat A}\) \( \newcommand\HB{\hat B}\) \( \newcommand\HC{\hat C}\) \( \newcommand\HD{\hat D}\) \( \newcommand\HE{\hat E}\) \( \newcommand\HF{\hat F}\) \( \newcommand\HG{\hat G}\) \( \newcommand\HH{\hat H}\) \( \newcommand\HI{\hat I}\) \( \newcommand\HJ{\hat J}\) \( \newcommand\HK{\hat K}\) \( \newcommand\HL{\hat L}\) \( \newcommand\HM{\hat M}\) \( \newcommand\HN{\hat N}\) \( \newcommand\HO{\hat O}\) \( \newcommand\HP{\hat P}\) \( \newcommand\HQ{\hat Q}\) \( \newcommand\HR{\hat R}\) \( \newcommand\HS{\hat S}\) \( \newcommand\HT{\hat T}\) \( \newcommand\HU{\hat U}\) \( \newcommand\HV{\hat V}\) \( \newcommand\HW{\hat W}\) \( \newcommand\HX{\hat X}\) \( \newcommand\HY{\hat Y}\) \( \newcommand\HZ{\hat Z}\) \( \newcommand\Halpha{\hat\alpha}\) \( \newcommand\Hbeta{\hat\beta}\) \( \newcommand\Hgamma{\hat\gamma}\) \( \newcommand\Hdelta{\hat\delta}\) \( \newcommand\Hepsilon{\hat\epsilon}\) \( \newcommand\Hvarepsilon{\hat\varepsilon}\) \( \newcommand\Hzeta{\hat\zeta}\) \( \newcommand\Heta{\hat\eta}\) \( \newcommand\Htheta{\hat\theta}\) \( \newcommand\Hvartheta{\hat\vartheta}\) \( \newcommand\Hiota{\hat\iota}\) \( \newcommand\Hkappa{\hat\kappa}\) \( \newcommand\Hlambda{\hat\lambda}\) \( \newcommand\Hmu{\hat\mu}\) \( \newcommand\Hnu{\hat\nu}\) \( \newcommand\Hxi{\hat\xi}\) \( \newcommand\Hom{\hat\omicron}\) \( \newcommand\Hpi{\hat\pi}\) \( \newcommand\Hvarpi{\hat\varpi}\) \( \newcommand\Hrho{\hat\rho}\) \( \newcommand\Hvarrho{\hat\varrho}\) \( \newcommand\Hsigma{\hat\sigma}\) \( \newcommand\Hvarsigma{\hat\varsigma}\) \( \newcommand\Htau{\var\tau}\) \( \newcommand\Hupsilon{\hat\upsilon}\) \( \newcommand\Hphi{\hat\phi}\) \( \newcommand\Hvarphi{\hat\varphi}\) \( \newcommand\Hchi{\hat\chi}\) \( \newcommand\Hxhi{\hat\xhi}\) \( \newcommand\Hpsi{\hat\psi}\) \( \newcommand\Homega{\hat\omega}\) \( \newcommand\HGamma{\hat\Gamma}\) \( \newcommand\HDelta{\hat\Delta}\) \( \newcommand\HTheta{\hat\Theta}\) \( \newcommand\HLambda{\hat\Lambda}\) \( \newcommand\HXi{\hat\Xi}\) \( \newcommand\HPi{\hat\Pi}\) \( \newcommand\HSigma{\hat\Sigma}\) \( \newcommand\HUps{\hat\Upsilon}\) \( \newcommand\HPhi{\hat\Phi}\) \( \newcommand\HPsi{\hat\Psi}\) \( \newcommand\HOmega{\hat\Omega}\) \( \newcommand\xhat{\hat\Bx}\) \( \newcommand\yhat{\hat\By}\) \( \newcommand\zhat{\hat\Bz}\) \( \newcommand\ehat{\hat\Be}\) \( \newcommand\khat{\hat\Bk}\) \( \newcommand\nhat{\hat\Bn}\) \( \newcommand\rhat{\hat\Br}\) \( \newcommand\phihat{\hat\Bphi}\) \( \newcommand\thetahat{\hat\Btheta}\) \( \newcommand\MA{\mathbb A}\) \( \newcommand\MB{\mathbb B}\) \( \newcommand\MC{\mathbb C}\) \( \newcommand\MD{\mathbb D}\) \( \newcommand\ME{\mathbb E}\) \( \newcommand\MF{\mathbb F}\) \( \newcommand\MG{\mathbb G}\) \( \newcommand\MH{\mathbb H}\) \( \newcommand\MI{\mathbb I}\) \( \newcommand\MJ{\mathbb J}\) \( \newcommand\MK{\mathbb K}\) \( \newcommand\ML{\mathbb L}\) \( \newcommand\MM{\mathbb M}\) \( \newcommand\MN{\mathbb N}\) \( \newcommand\MO{\mathbb O}\) \( \newcommand\MP{\mathbb P}\) \( \newcommand\MQ{\mathbb Q}\) \( \newcommand\MR{\mathbb R}\) \( \newcommand\MS{\mathbb S}\) \( \newcommand\MT{\mathbb T}\) \( \newcommand\MU{\mathbb U}\) \( \newcommand\MV{\mathbb V}\) \( \newcommand\MW{\mathbb W}\) \( \newcommand\MX{\mathbb X}\) \( \newcommand\MY{\mathbb Y}\) \( \newcommand\MZ{\mathbb Z}\) \( \newcommand\CA{\mathcal A}\) \( \newcommand\CB{\mathcal B}\) \( \newcommand\CC{\mathcal C}\) \( \newcommand\CD{\mathcal D}\) \( \newcommand\CE{\mathcal E}\) \( \newcommand\CF{\mathcal F}\) \( \newcommand\CG{\mathcal G}\) \( \newcommand\CH{\mathcal H}\) \( \newcommand\CI{\mathcal I}\) \( \newcommand\CJ{\mathcal J}\) \( \newcommand\CK{\mathcal K}\) \( \newcommand\CL{\mathcal L}\) \( \newcommand\CM{\mathcal M}\) \( \newcommand\CN{\mathcal N}\) \( \newcommand\CO{\mathcal O}\) \( \newcommand\CP{\mathcal P}\) \( \newcommand\CQ{\mathcal Q}\) \( \newcommand\CR{\mathcal R}\) \( \newcommand\CS{\mathcal S}\) \( \newcommand\CT{\mathcal T}\) \( \newcommand\CU{\mathcal U}\) \( \newcommand\CV{\mathcal V}\) \( \newcommand\CW{\mathcal W}\) \( \newcommand\CX{\mathcal X}\) \( \newcommand\CY{\mathcal Y}\) \( \newcommand\CZ{\mathcal Z}\) \( \newcommand\Fa{\mathfrak a}\) \( \newcommand\Fb{\mathfrak b}\) \( \newcommand\Fc{\mathfrak c}\) \( \newcommand\Fd{\mathfrak d}\) \( \newcommand\Fe{\mathfrak e}\) \( \newcommand\Ff{\mathfrak f}\) \( \newcommand\Fg{\mathfrak g}\) \( \newcommand\Fh{\mathfrak h}\) \( \newcommand\Fi{\mathfrak i}\) \( \newcommand\Fj{\mathfrak j}\) \( \newcommand\Fk{\mathfrak k}\) \( \newcommand\Fl{\mathfrak l}\) \( \newcommand\Fm{\mathfrak m}\) \( \newcommand\Fn{\mathfrak n}\) \( \newcommand\Fo{\mathfrak o}\) \( \newcommand\Fp{\mathfrak p}\) \( \newcommand\Fq{\mathfrak q}\) \( \newcommand\Fr{\mathfrak r}\) \( \newcommand\Fs{\mathfrak s}\) \( \newcommand\Ft{\mathfrak t}\) \( \newcommand\Fu{\mathfrak u}\) \( \newcommand\Fv{\mathfrak v}\) \( \newcommand\Fw{\mathfrak w}\) \( \newcommand\Fx{\mathfrak x}\) \( \newcommand\Fy{\mathfrak y}\) \( \newcommand\Fz{\mathfrak z}\) \( \newcommand\FA{\mathfrak A}\) \( \newcommand\FB{\mathfrak B}\) \( \newcommand\FC{\mathfrak C}\) \( \newcommand\FD{\mathfrak D}\) \( \newcommand\FE{\mathfrak E}\) \( \newcommand\FF{\mathfrak F}\) \( \newcommand\FG{\mathfrak G}\) \( \newcommand\FH{\mathfrak H}\) \( \newcommand\FI{\mathfrak I}\) \( \newcommand\FJ{\mathfrak J}\) \( \newcommand\FK{\mathfrak K}\) \( \newcommand\FL{\mathfrak L}\) \( \newcommand\FM{\mathfrak M}\) \( \newcommand\FN{\mathfrak N}\) \( \newcommand\FO{\mathfrak O}\) \( \newcommand\FP{\mathfrak P}\) \( \newcommand\FQ{\mathfrak Q}\) \( \newcommand\FR{\mathfrak R}\) \( \newcommand\FS{\mathfrak S}\) \( \newcommand\FT{\mathfrak T}\) \( \newcommand\FU{\mathfrak U}\) \( \newcommand\FV{\mathfrak V}\) \( \newcommand\FW{\mathfrak W}\) \( \newcommand\FX{\mathfrak X}\) \( \newcommand\FY{\mathfrak Y}\) \( \newcommand\FZ{\mathfrak Z}\) \( \newcommand\Da{\dot a}\) \( \newcommand\Db{\dot b}\) \( \newcommand\Dc{\dot c}\) \( \newcommand\Dd{\dot d}\) \( \newcommand\De{\dot e}\) \( \newcommand\Df{\dot f}\) \( \newcommand\Dg{\dot g}\) \( \newcommand\Dh{\dot h}\) \( \newcommand\Di{\dot \imath}\) \( \newcommand\Dj{\dot \jmath}\) \( \newcommand\Dk{\dot k}\) \( \newcommand\Dl{\dot l}\) \( \newcommand\Dm{\dot m}\) \( \newcommand\Dn{\dot n}\) \( \newcommand\Do{\dot o}\) \( \newcommand\Dp{\dot p}\) \( \newcommand\Dq{\dot q}\) \( \newcommand\Dr{\dot r}\) \( \newcommand\Ds{\dot s}\) \( \newcommand\Dt{\dot t}\) \( \newcommand\Du{\dot u}\) \( \newcommand\Dv{\dot v}\) \( \newcommand\Dw{\dot w}\) \( \newcommand\Dx{\dot x}\) \( \newcommand\Dy{\dot y}\) \( \newcommand\Dz{\dot z}\) \( \newcommand\DA{\dot A}\) \( \newcommand\DB{\dot B}\) \( \newcommand\DC{\dot C}\) \( \newcommand\DD{\dot D}\) \( \newcommand\DE{\dot E}\) \( \newcommand\DF{\dot F}\) \( \newcommand\DG{\dot G}\) \( \newcommand\DH{\dot H}\) \( \newcommand\DI{\dot I}\) \( \newcommand\DJ{\dot J}\) \( \newcommand\DK{\dot K}\) \( \newcommand\DL{\dot L}\) \( \newcommand\DM{\dot M}\) \( \newcommand\DN{\dot N}\) \( \newcommand\DO{\dot O}\) \( \newcommand\DP{\dot P}\) \( \newcommand\DQ{\dot Q}\) \( \newcommand\DR{\dot R}\) \( \newcommand\DS{\dot S}\) \( \newcommand\DT{\dot T}\) \( \newcommand\DU{\dot U}\) \( \newcommand\DV{\dot V}\) \( \newcommand\DW{\dot W}\) \( \newcommand\DX{\dot X}\) \( \newcommand\DY{\dot Y}\) \( \newcommand\DZ{\dot Z}\) \( \newcommand\Dalpha ParseError: invalid DekiScript (click for details) Callstack: at (Template:MathJaxArovas), /content/body/div/p[1]/span[1], line 1, column 1 at template() at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/04:_Statistical_Ensembles/4.07:_Ideal_Gas_Statistical_Mechanics), /content/body/p[1]/span, line 1, column 23 \) \( \newcommand\Dbeta ParseError: invalid DekiScript (click for details) Callstack: at (Template:MathJaxArovas), /content/body/div/p[1]/span[2], line 1, column 1 at template() at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/04:_Statistical_Ensembles/4.07:_Ideal_Gas_Statistical_Mechanics), /content/body/p[1]/span, line 1, column 23 \) \( \newcommand\Dgamma ParseError: invalid DekiScript (click for details) Callstack: at (Template:MathJaxArovas), /content/body/div/p[1]/span[3], line 1, column 1 at template() at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/04:_Statistical_Ensembles/4.07:_Ideal_Gas_Statistical_Mechanics), /content/body/p[1]/span, line 1, column 23 \) \( \newcommand\Ddelta ParseError: invalid DekiScript (click for details) Callstack: at (Template:MathJaxArovas), /content/body/div/p[1]/span[4], line 1, column 1 at template() at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/04:_Statistical_Ensembles/4.07:_Ideal_Gas_Statistical_Mechanics), /content/body/p[1]/span, line 1, column 23 \) \( \newcommand\Depsilon ParseError: invalid DekiScript (click for details) Callstack: at (Template:MathJaxArovas), /content/body/div/p[1]/span[5], line 1, column 1 at template() at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/04:_Statistical_Ensembles/4.07:_Ideal_Gas_Statistical_Mechanics), /content/body/p[1]/span, line 1, column 23 \) \( \newcommand\Dvarepsilon ParseError: invalid DekiScript (click for details) Callstack: at (Template:MathJaxArovas), /content/body/div/p[1]/span[6], line 1, column 1 at template() at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/04:_Statistical_Ensembles/4.07:_Ideal_Gas_Statistical_Mechanics), /content/body/p[1]/span, line 1, column 23 \) \( \newcommand\Dzeta ParseError: invalid DekiScript (click for details) Callstack: at (Template:MathJaxArovas), /content/body/div/p[1]/span[7], line 1, column 1 at template() at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/04:_Statistical_Ensembles/4.07:_Ideal_Gas_Statistical_Mechanics), /content/body/p[1]/span, line 1, column 23 \) \( \newcommand\Deta ParseError: invalid DekiScript (click for details) Callstack: at (Template:MathJaxArovas), /content/body/div/p[1]/span[8], line 1, column 1 at template() at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/04:_Statistical_Ensembles/4.07:_Ideal_Gas_Statistical_Mechanics), /content/body/p[1]/span, line 1, column 23 \) \( \newcommand\Dtheta ParseError: invalid DekiScript (click for details) Callstack: at (Template:MathJaxArovas), /content/body/div/p[1]/span[9], line 1, column 1 at template() at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/04:_Statistical_Ensembles/4.07:_Ideal_Gas_Statistical_Mechanics), /content/body/p[1]/span, line 1, column 23 \) \( \newcommand\Dvartheta ParseError: invalid DekiScript (click for details) Callstack: at (Template:MathJaxArovas), /content/body/div/p[1]/span[10], line 1, column 1 at template() at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/04:_Statistical_Ensembles/4.07:_Ideal_Gas_Statistical_Mechanics), /content/body/p[1]/span, line 1, column 23 \) \( \newcommand\Diota ParseError: invalid DekiScript (click for details) Callstack: at (Template:MathJaxArovas), /content/body/div/p[1]/span[11], line 1, column 1 at template() at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/04:_Statistical_Ensembles/4.07:_Ideal_Gas_Statistical_Mechanics), /content/body/p[1]/span, line 1, column 23 \) \( \newcommand\Dkappa ParseError: invalid DekiScript (click for details) Callstack: at (Template:MathJaxArovas), /content/body/div/p[1]/span[12], line 1, column 1 at template() at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/04:_Statistical_Ensembles/4.07:_Ideal_Gas_Statistical_Mechanics), /content/body/p[1]/span, line 1, column 23 \) \( \newcommand\Dlambda ParseError: invalid DekiScript (click for details) Callstack: at (Template:MathJaxArovas), /content/body/div/p[1]/span[13], line 1, column 1 at template() at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/04:_Statistical_Ensembles/4.07:_Ideal_Gas_Statistical_Mechanics), /content/body/p[1]/span, line 1, column 23 \) \( \newcommand\Dmu{\dot\mu}\) \( \newcommand\Dnu{\dot\nu}\) \( \newcommand\Dxi{\dot\xi}\) \( \newcommand\Dom{\dot\omicron}\) \( \newcommand\Dpi{\dot\pi}\) \( \newcommand\Dvarpi ParseError: invalid DekiScript (click for details) Callstack: at (Template:MathJaxArovas), /content/body/div/p[1]/span[14], line 1, column 1 at template() at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/04:_Statistical_Ensembles/4.07:_Ideal_Gas_Statistical_Mechanics), /content/body/p[1]/span, line 1, column 23 \) \( \newcommand\Drho{\dot\rho}\) \( \newcommand\Dvarrho{\dot\varrho}\) \( \newcommand\Dsigma{\dot\sigma}\) \( \newcommand\Dvarsigma{\dot\varsigma}\) \( \newcommand\Dtau{\var\tau}\) \( \newcommand\Dupsilon{\dot\upsilon}\) \( \newcommand\Dphi{\dot\phi}\) \( \newcommand\Dvarphi{\dot\varphi}\) \( \newcommand\Dchi{\dot\chi}\) \( \newcommand\Dpsi{\dot\psi}\) \( \newcommand\Domega{\dot\omega}\) \( \newcommand\DGamma ParseError: invalid DekiScript (click for details) Callstack: at (Template:MathJaxArovas), /content/body/div/p[1]/span[15], line 1, column 1 at template() at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/04:_Statistical_Ensembles/4.07:_Ideal_Gas_Statistical_Mechanics), /content/body/p[1]/span, line 1, column 23 \) \( \newcommand\DDelta ParseError: invalid DekiScript (click for details) Callstack: at (Template:MathJaxArovas), /content/body/div/p[1]/span[16], line 1, column 1 at template() at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/04:_Statistical_Ensembles/4.07:_Ideal_Gas_Statistical_Mechanics), /content/body/p[1]/span, line 1, column 23 \) \( \newcommand\DTheta ParseError: invalid DekiScript (click for details) Callstack: at (Template:MathJaxArovas), /content/body/div/p[1]/span[17], line 1, column 1 at template() at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/04:_Statistical_Ensembles/4.07:_Ideal_Gas_Statistical_Mechanics), /content/body/p[1]/span, line 1, column 23 \) \( \newcommand\DLambda{\dot\Lambda}\) \( \newcommand\DXi{\dot\Xi}\) \( \newcommand\DPi{\dot\Pi}\) \( \newcommand\DSigma{\dot\Sigma}\) \( \newcommand\DUps{\dot\Upsilon}\) \( \newcommand\DPhi{\dot\Phi}\) \( \newcommand\DPsi{\dot\Psi}\) \( \newcommand\DOmega{\dot\Omega}\) \( \newcommand\Va{\vec a}\) \( \newcommand\Vb{\vec b}\) \( \newcommand\Vc{\vec c}\) \( \newcommand\Vd{\vec d}\) \( \newcommand\Ve{\vec e}\) \( \newcommand\Vf{\vec f}\) \( \newcommand\Vg{\vec g}\) \( \newcommand\Vh{\vec h}\) \( \newcommand\Vi{\vec \imath}\) \( \newcommand\Vj{\vec \jmath}\) \( \newcommand\Vk{\vec k}\) \( \newcommand\Vl{\vec l}\) \( \newcommand\Vm{\vec m}\) \( \newcommand\Vn{\vec n}\) \( \newcommand\Vo{\vec o}\) \( \newcommand\Vp{\vec p}\) \( \newcommand\Vq{\vec q}\) \( \newcommand\Vr{\vec r}\) \( \newcommand\Vs{\vec s}\) \( \newcommand\Vt{\vec t}\) \( \newcommand\Vu{\vec u}\) \( \newcommand\Vv{\vec v}\) \( \newcommand\Vw{\vec w}\) \( \newcommand\Vx{\vec x}\) \( \newcommand\Vy{\vec y}\) \( \newcommand\Vz{\vec z}\) \( \newcommand\VA{\vec A}\) \( \newcommand\VB{\vec B}\) \( \newcommand\VC{\vec C}\) \( \newcommand\VD{\vec D}\) \( \newcommand\VE{\vec E}\) \( \newcommand\VF{\vec F}\) \( \newcommand\VG{\vec G}\) \( \newcommand\VH{\vec H}\) \( \newcommand\VI{\vec I}\) \( \newcommand\VJ{\vec J}\) \( \newcommand\VK{\vec K}\) \( \newcommand\VL{\vec L}\) \( \newcommand\VM{\vec M}\) \( \newcommand\VN{\vec N}\) \( \newcommand\VO{\vec O}\) \( \newcommand\VP{\vec P}\) \( \newcommand\VQ{\vec Q}\) \( \newcommand\VR{\vec R}\) \( \newcommand\VS{\vec S}\) \( \newcommand\VT{\vec T}\) \( \newcommand\VU{\vec U}\) \( \newcommand\VV{\vec V}\) \( \newcommand\VW{\vec W}\) \( \newcommand\VX{\vec X}\) \( \newcommand\VY{\vec Y}\) \( \newcommand\VZ{\vec Z}\) \( \newcommand\Valpha{\vec\alpha}\) \( \newcommand\Vbeta{\vec\beta}\) \( \newcommand\Vgamma{\vec\gamma}\) \( \newcommand\Vdelta{\vec\delta}\) \( \newcommand\Vepsilon{\vec\epsilon}\) \( \newcommand\Vvarepsilon{\vec\varepsilon}\) \( \newcommand\Vzeta{\vec\zeta}\) \( \newcommand\Veta{\vec\eta}\) \( \newcommand\Vtheta{\vec\theta}\) \( \newcommand\Vvartheta{\vec\vartheta}\) \( \newcommand\Viota{\vec\iota}\) \( \newcommand\Vkappa{\vec\kappa}\) \( \newcommand\Vlambda{\vec\lambda}\) \( \newcommand\Vmu ParseError: invalid DekiScript (click for details) Callstack: at (Template:MathJaxArovas), /content/body/div/p[1]/span[18], line 1, column 1 at template() at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/04:_Statistical_Ensembles/4.07:_Ideal_Gas_Statistical_Mechanics), /content/body/p[1]/span, line 1, column 23 \) \( \newcommand\Vnu ParseError: invalid DekiScript (click for details) Callstack: at (Template:MathJaxArovas), /content/body/div/p[1]/span[19], line 1, column 1 at template() at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/04:_Statistical_Ensembles/4.07:_Ideal_Gas_Statistical_Mechanics), /content/body/p[1]/span, line 1, column 23 \) \( \newcommand\Vxi ParseError: invalid DekiScript (click for details) Callstack: at (Template:MathJaxArovas), /content/body/div/p[1]/span[20], line 1, column 1 at template() at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/04:_Statistical_Ensembles/4.07:_Ideal_Gas_Statistical_Mechanics), /content/body/p[1]/span, line 1, column 23 \) \( \newcommand\Vom ParseError: invalid DekiScript (click for details) Callstack: at (Template:MathJaxArovas), /content/body/div/p[1]/span[21], line 1, column 1 at template() at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/04:_Statistical_Ensembles/4.07:_Ideal_Gas_Statistical_Mechanics), /content/body/p[1]/span, line 1, column 23 \) \( \newcommand\Vpi ParseError: invalid DekiScript (click for details) Callstack: at (Template:MathJaxArovas), /content/body/div/p[1]/span[22], line 1, column 1 at template() at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/04:_Statistical_Ensembles/4.07:_Ideal_Gas_Statistical_Mechanics), /content/body/p[1]/span, line 1, column 23 \) \( \newcommand\Vvarpi ParseError: invalid DekiScript (click for details) Callstack: at (Template:MathJaxArovas), /content/body/div/p[1]/span[23], line 1, column 1 at template() at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/04:_Statistical_Ensembles/4.07:_Ideal_Gas_Statistical_Mechanics), /content/body/p[1]/span, line 1, column 23 \) \( \newcommand\Vrho ParseError: invalid DekiScript (click for details) Callstack: at (Template:MathJaxArovas), /content/body/div/p[1]/span[24], line 1, column 1 at template() at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/04:_Statistical_Ensembles/4.07:_Ideal_Gas_Statistical_Mechanics), /content/body/p[1]/span, line 1, column 23 \) \( \newcommand\Vvarrho ParseError: invalid DekiScript (click for details) Callstack: at (Template:MathJaxArovas), /content/body/div/p[1]/span[25], line 1, column 1 at template() at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/04:_Statistical_Ensembles/4.07:_Ideal_Gas_Statistical_Mechanics), /content/body/p[1]/span, line 1, column 23 \) \( \newcommand\Vsigma ParseError: invalid DekiScript (click for details) Callstack: at (Template:MathJaxArovas), /content/body/div/p[1]/span[26], line 1, column 1 at template() at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/04:_Statistical_Ensembles/4.07:_Ideal_Gas_Statistical_Mechanics), /content/body/p[1]/span, line 1, column 23 \) \( \newcommand\Vvarsigma ParseError: invalid DekiScript (click for details) Callstack: at (Template:MathJaxArovas), /content/body/div/p[1]/span[27], line 1, column 1 at template() at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/04:_Statistical_Ensembles/4.07:_Ideal_Gas_Statistical_Mechanics), /content/body/p[1]/span, line 1, column 23 \) \( \newcommand\Vtau ParseError: invalid DekiScript (click for details) Callstack: at (Template:MathJaxArovas), /content/body/div/p[1]/span[28], line 1, column 1 at template() at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/04:_Statistical_Ensembles/4.07:_Ideal_Gas_Statistical_Mechanics), /content/body/p[1]/span, line 1, column 23 \) \( \newcommand\Vupsilon ParseError: invalid DekiScript (click for details) Callstack: at (Template:MathJaxArovas), /content/body/div/p[1]/span[29], line 1, column 1 at template() at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/04:_Statistical_Ensembles/4.07:_Ideal_Gas_Statistical_Mechanics), /content/body/p[1]/span, line 1, column 23 \) \( \newcommand\Vphi ParseError: invalid DekiScript (click for details) Callstack: at (Template:MathJaxArovas), /content/body/div/p[1]/span[30], line 1, column 1 at template() at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/04:_Statistical_Ensembles/4.07:_Ideal_Gas_Statistical_Mechanics), /content/body/p[1]/span, line 1, column 23 \) \( \newcommand\Vvarphi ParseError: invalid DekiScript (click for details) Callstack: at (Template:MathJaxArovas), /content/body/div/p[1]/span[31], line 1, column 1 at template() at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/04:_Statistical_Ensembles/4.07:_Ideal_Gas_Statistical_Mechanics), /content/body/p[1]/span, line 1, column 23 \) \( \newcommand\Vchi ParseError: invalid DekiScript (click for details) Callstack: at (Template:MathJaxArovas), /content/body/div/p[1]/span[32], line 1, column 1 at template() at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/04:_Statistical_Ensembles/4.07:_Ideal_Gas_Statistical_Mechanics), /content/body/p[1]/span, line 1, column 23 \) \( \newcommand\Vpsi ParseError: invalid DekiScript (click for details) Callstack: at (Template:MathJaxArovas), /content/body/div/p[1]/span[33], line 1, column 1 at template() at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/04:_Statistical_Ensembles/4.07:_Ideal_Gas_Statistical_Mechanics), /content/body/p[1]/span, line 1, column 23 \) \( \newcommand\Vomega ParseError: invalid DekiScript (click for details) Callstack: at (Template:MathJaxArovas), /content/body/div/p[1]/span[34], line 1, column 1 at template() at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/04:_Statistical_Ensembles/4.07:_Ideal_Gas_Statistical_Mechanics), /content/body/p[1]/span, line 1, column 23 \) \( \newcommand\VGamma ParseError: invalid DekiScript (click for details) Callstack: at (Template:MathJaxArovas), /content/body/div/p[1]/span[35], line 1, column 1 at template() at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/04:_Statistical_Ensembles/4.07:_Ideal_Gas_Statistical_Mechanics), /content/body/p[1]/span, line 1, column 23 \) \( \newcommand\VDelta ParseError: invalid DekiScript (click for details) Callstack: at (Template:MathJaxArovas), /content/body/div/p[1]/span[36], line 1, column 1 at template() at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/04:_Statistical_Ensembles/4.07:_Ideal_Gas_Statistical_Mechanics), /content/body/p[1]/span, line 1, column 23 \) \( \newcommand\VTheta{\vec\Theta}\) \( \newcommand\VLambda{\vec\Lambda}\) \( \newcommand\VXi{\vec\Xi}\) \( \newcommand\VPi{\vec\Pi}\) \( \newcommand\VSigma{\vec\Sigma}\) \( \newcommand\VUps{\vec\Upsilon}\) \( \newcommand\VPhi{\vec\Phi}\) \( \newcommand\VPsi{\vec\Psi}\) \( \newcommand\VOmega{\vec\Omega}\) \( \newcommand\BA{\mib A}\) \( \newcommand\BB{\mib B}\) \( \newcommand\BC{\mib C}\) \( \newcommand\BD{\mib D}\) \( \newcommand\BE{\mib E}\) \( \newcommand\BF{\mib F}\) \( \newcommand\BG{\mib G}\) \( \newcommand\BH{\mib H}\) \( \newcommand\BI{\mib I}}\) \( \newcommand\BJ{\mib J}\) \( \newcommand\BK{\mib K}\) \( \newcommand\BL{\mib L}\) \( \newcommand\BM{\mib M}\) \( \newcommand\BN{\mib N}\) \( \newcommand\BO{\mib O}\) \( \newcommand\BP{\mib P}\) \( \newcommand\BQ{\mib Q}\) \( \newcommand\BR{\mib R}\) \( \newcommand\BS{\mib S}\) \( \newcommand\BT{\mib T}\) \( \newcommand\BU{\mib U}\) \( \newcommand\BV{\mib V}\) \( \newcommand\BW{\mib W}\) \( \newcommand\BX{\mib X}\) \( \newcommand\BY{\mib Y}\) \( \newcommand\BZ{\mib Z}\) \( \newcommand\Ba{\mib a}\) \( \newcommand\Bb{\mib b}\) \( \newcommand\Bc{\mib c}\) \( \newcommand\Bd{\mib d}\) \( \newcommand\Be{\mib e}\) \( \newcommand\Bf{\mib f}\) \( \newcommand\Bg{\mib g}\) \( \newcommand\Bh{\mib h}\) \( \newcommand\Bi{\mib i}\) \( \newcommand\Bj{\mib j}\) \( \newcommand\Bk{\mib k}\) \( \newcommand\Bl{\mib l}\) \( \newcommand\Bm{\mib m}\) \( \newcommand\Bn{\mib n}\) \( \newcommand\Bo{\mib o}\) \( \newcommand\Bp{\mib p}\) \( \newcommand\Bq{\mib q}\) \( \newcommand\Br{\mib r}\) \( \newcommand\Bs{\mib s}\) \( \newcommand\Bt{\mib t}\) \( \newcommand\Bu{\mib u}\) \( \newcommand\Bv{\mib v}\) \( \newcommand\Bw{\mib w}\) \( \newcommand\Bx{\mib x}\) \( \newcommand\By{\mib y}\) \( \newcommand\Bz{\mib z}\)\) \( \newcommand\vrh{\varrho}\) \( \newcommand\vsig{\varsigma}\) \( \newcommand\ups{\upsilon}\) \( \newcommand\eps{\epsilon}\) \( \newcommand\ve{\varepsilon}\) \( \newcommand\vth{\vartheta}\) \( \newcommand\vphi{\varphi}\) \( \newcommand\xhi{\chi}\) \( \newcommand\Ups{\Upsilon}\) \( \newcommand\Balpha{\mib\alpha}\) \( \newcommand\Bbeta{\mib\beta}\) \( \newcommand\Bgamma{\mib\gamma}\) \( \newcommand\Bdelta{\mib\delta}\) \( \newcommand\Beps{\mib\epsilon}\) \( \newcommand\Bve{\mib\varepsilon}\) \( \newcommand\Bzeta{\mib\zeta}\) \( \newcommand\Beta{\mib\eta}\) \( \newcommand\Btheta{\mib\theta}\) \( \newcommand\Bvth{\mib\vartheta}\) \( \newcommand\Biota{\mib\iota}\) \( \newcommand\Bkappa{\mib\kappa}\) \( \newcommand\Blambda{\mib\lambda}\) \( \newcommand\Bmu{\mib\mu}\) \( \newcommand\Bnu{\mib\nu}\) \( \newcommand\Bxi{\mib\xi}\) \( \newcommand\Bom{\mib\omicron}\) \( \newcommand\Bpi{\mib\pi}\) \( \newcommand\Bvarpi{\mib\varpi}\) \( \newcommand\Brho{\mib\rho}\) \( \newcommand\Bvrh{\mib\varrho}\) \( \newcommand\Bsigma{\mib\sigma}\) \( \newcommand\Bvsig{\mib\varsigma}\) \( \newcommand\Btau{\mib\tau}\) \( \newcommand\Bups{\mib\upsilon}\) \( \newcommand\Bphi{\mib\phi}\) \( \newcommand\Bvphi{\mib\vphi}\) \( \newcommand\Bchi{\mib\chi}\) \( \newcommand\Bpsi{\mib\psi}\) \( \newcommand\Bomega{\mib\omega}\) \( \newcommand\BGamma{\mib\Gamma}\) \( \newcommand\BDelta{\mib\Delta}\) \( \newcommand\BTheta{\mib\Theta}\) \( \newcommand\BLambda{\mib\Lambda}\) \( \newcommand\BXi{\mib\Xi}\) \( \newcommand\BPi{\mib\Pi}\) \( \newcommand\BSigma{\mib\Sigma}\) \( \newcommand\BUps{\mib\Upsilon}\) \( \newcommand\BPhi{\mib\Phi}\) \( \newcommand\BPsi{\mib\Psi}\) \( \newcommand\BOmega{\mib\Omega}\) \( \newcommand\Bxhi{\raise.35ex\hbox{$\Bchi$}}\) \( \newcommand\RGamma{ \Gamma}\) \( \newcommand\RDelta{ \Delta}\) \( \newcommand\RTheta{ \Theta}\) \( \newcommand\RLambda{ \Lambda}\) \( \newcommand\RXi{ \Xi}\) \( \newcommand\RPi{ \Pi}\) \( \newcommand\RSigma{ \Sigma}\) \( \newcommand\RUps{ \Upsilon}\) \( \newcommand\RPhi{ \Phi}\) \( \newcommand\RPsi{ \Psi}\) \( \newcommand\ROmega{ \Omega}\) \( \newcommand\RA{ A}\) \( \newcommand\RB{ B}\) \( \newcommand\RC{ C}\) \( \newcommand\RD{ D}\) \( \newcommand\RE{ E}\) \( \newcommand\RF{ F}\) \( \newcommand\RG{ G}\) \( \newcommand\RH{ H}\) \( \newcommand\RI{ I}\) \( \newcommand\RJ{ J}\) \( \newcommand\RK{ K}\) \( \newcommand\RL{ L}\) \( \newcommand { M}\) \( \newcommand\RN{ N}\) \( \newcommand\RO{ O}\) \( \newcommand\RP{ P}\) \( \newcommand\RQ{ Q}\) \( \newcommand\RR{ R}\) \( \newcommand\RS{ S}\) \( \newcommand\RT{ T}\) \( \newcommand\RU{ U}\) \( \newcommand\RV{ V}\) \( \newcommand\RW{ W}\) \( \newcommand\RX{ X}\) \( \newcommand\RY{ Y}\) \( \newcommand\RZ{ Z}\) \( \newcommand\Ra{ a}\) \( \newcommand\Rb{ b}\) \( \newcommand\Rc{ c}\) \( \newcommand\Rd{ d}\) \( \newcommand\Re{ e}\) \( \newcommand\Rf{ f}\) \( \newcommand\Rg{ g}\) \( \newcommand\Rh{ h}\) \( \newcommand\Ri{ i}\) \( \newcommand\Rj{ j}\) \( \newcommand\Rk{ k}\) \( \newcommand\Rl{ l}\) \( \newcommand { m}\) \( \newcommand\Rn{ n}\) \( \newcommand\Ro{ o}\) \( \newcommand\Rp{ p}\) \( \newcommand\Rq{ q}\) \( \newcommand\Rr{ r}\) \( \newcommand\Rs{ s}\) \( \newcommand\Rt{ t}\) \( \newcommand\Ru{ u}\) \( \newcommand\Rv{ v}\) \( \newcommand\Rw{ w}\) \( \newcommand\Rx{ x}\) \( \newcommand\Ry{ y}\) \( \newcommand\Rz{ z}\) \( \newcommand\BBA{\boldsymbol\RA}\) \( \newcommand\BBB{\boldsymbol\RB}\) \( \newcommand\BBC{\boldsymbol\RC}\) \( \newcommand\BBD{\boldsymbol\RD}\) \( \newcommand\BBE{\boldsymbol\RE}\) \( \newcommand\BBF{\boldsymbol\RF}\) \( \newcommand\BBG{\boldsymbol\RG}\) \( \newcommand\BBH{\boldsymbol\RH}\) \( \newcommand\BBI{\boldsymbol\RI}\) \( \newcommand\BBJ{\boldsymbol\RJ}\) \( \newcommand\BBK{\boldsymbol\RK}\) \( \newcommand\BBL{\boldsymbol\RL}\) \( \newcommand\BBM{\boldsymbol }\) \( \newcommand\BBN{\boldsymbol\RN}\) \( \newcommand\BBO{\boldsymbol\RO}\) \( \newcommand\BBP{\boldsymbol\RP}\) \( \newcommand\BBQ{\boldsymbol\RQ}\) \( \newcommand\BBR{\boldsymbol\RR}\) \( \newcommand\BBS{\boldsymbol\RS}\) \( \newcommand\BBT{\boldsymbol\RT}\) \( \newcommand\BBU{\boldsymbol\RU}\) \( \newcommand\BBV{\boldsymbol\RV}\) \( \newcommand\BBW{\boldsymbol\RW}\) \( \newcommand\BBX{\boldsymbol\RX}\) \( \newcommand\BBY{\boldsymbol\RY}\) \( \newcommand\BBZ{\boldsymbol\RZ}\) \( \newcommand\BBa{\boldsymbol\Ra}\) \( \newcommand\BBb{\boldsymbol\Rb}\) \( \newcommand\BBc{\boldsymbol\Rc}\) \( \newcommand\BBd{\boldsymbol\Rd}\) \( \newcommand\BBe{\boldsymbol\Re}\) \( \newcommand\BBf{\boldsymbol\Rf}\) \( \newcommand\BBg{\boldsymbol\Rg}\) \( \newcommand\BBh{\boldsymbol\Rh}\}\) \( \newcommand\BBi{\boldsymbol\Ri}\) \( \newcommand\BBj{\boldsymbol\Rj}\) \( \newcommand\BBk{\boldsymbol\Rk}\) \( \newcommand\BBl{boldsymbol\Rl}\) \( \newcommand\BBm{\boldsymbol }\) \( \newcommand\BBn{\boldsymbol\Rn}\) \( \newcommand\BBo{\boldsymbol\Ro}\) \( \newcommand\BBp{\boldsymbol\Rp}\) \( \newcommand\BBq{\boldsymbol\Rq}\) \( \newcommand\BBr{\boldsymbol\Rr}\) \( \newcommand\BBs{\boldsymbol\Rs}\) \( \newcommand\BBt{\boldsymbol\Rt}\) \( \newcommand\BBu{\boldsymbol\Ru}\) \( \newcommand\BBv{\boldsymbol\Rv}\) \( \newcommand\BBw{\boldsymbol\Rw}\) \( \newcommand\BBx{\boldsymbol\Rx}\) \( \newcommand\BBy{\boldsymbol\Ry}\) \( \newcommand\BBz{\boldsymbol\Rz}\) \( \newcommand\tcb{\textcolor{blue}\) \( \newcommand\tcr{\textcolor{red}\) \( \newcommand\bnabla{\boldsymbol{\nabla}}\) \( \newcommand\Bell{\boldsymbol\ell}\) \( \newcommand\dbar{\,{\mathchar'26\mkern-12mu d}} \) \( \newcommand\ns{^\vphantom{*}}\) \( \newcommand\uar{\uparrow}\) \( \newcommand\dar{\downarrow}\) \( \newcommand\impi{\int\limits_{-\infty}^{\infty}\!\!}\) \( \newcommand\izpi{\int\limits_{0}^{\infty}\!\!}\) \( \newcommand\etc{\it etc.\/}\) \( \newcommand\etal{\it et al.\/}\) \( \newcommand\opcit{\it op. cit.\/}\) \( \newcommand\ie{\it i.e.\/}\) \( \newcommand\Ie{\it I.e.\/}\) \( \newcommand\viz{\it viz.\/}\) \( \newcommand\eg{\it e.g.\/}\) \( \newcommand\Eg{\it E.g.\/}\) \( \newcommand\dbar{\,{\mathchar'26\mkern-12mu d}} \) \( \def\sss#1{\scriptscriptstyle #1}\) \( \def\ss#1{\scriptstyle #1}\) \( \def\ssr#1{\scriptstyle #1}\) \( \def\ssf#1{\scriptstyle #1}\) \( \newcommand\NA{N_{\ssr{\!A}}}\) \( \newcommand\lala{\langle\!\langle}\) \( \newcommand\rara{\rangle\!\rangle}\) \( \newcommand\blan{\big\langle}\) \( \newcommand\bran{\big\rangle}\) \( \newcommand\Blan{\Big\langle}\) \( \newcommand\Bran{\Big\rangle}\) \( \newcommand\intl{\int\limits}\) \( \newcommand\half{\frac{1}{2}}\) \( \newcommand\third{\frac{1}{3}}\) \( \newcommand\fourth{\frac{1}{4}}\) \( \newcommand\eighth{\frac{1}{8}}\) \( \newcommand\uar{\uparrow}\) \( \newcommand\dar{\downarrow}\) \( \newcommand\undertext#1{$\underline{\hbox{#1}}$}\) \( \newcommand\Tra{\mathop{\textsf{Tr}}\,}\) \( \newcommand\det{\mathop{\textsf{det}}\,}\) \( \def\tket#1{|  #1 \rangle}\) \( \def\tbra#1{\langle #1|}\) \( \def\tbraket#1#2{\langle #1  |   #2 \rangle}\) \( \def\texpect#1#2#3{\langle #1 |   #2  |  #3 \rangle}\) \( \def\sket#1{|  \, #1 \,  \rangle}\) \( \def\sbra#1{\langle \,  #1 \, |}\) \( \def\sbraket#1#2{\langle \, #1  \, |  \, #2 \,  \rangle}\) \( \def\sexpect#1#2#3{\langle \, #1 \, | \,  #2  \, | \, #3 \, \rangle}\) \(\def\ket#1{\big| \, #1\, \big\rangle}\) \( \def\bra#1{\big\langle \, #1 \, \big|}\) \( \def\braket#1#2{\big\langle \, #1\, \big| \,#2 \,\big\rangle}\) \( \def\expect#1#2#3{\big\langle\, #1\, \big|\, #2\, \big| \,#3\, \big\rangle}\) \( \newcommand\pz{\partial}\) \( \newcommand\pzb{\bar{\partial}}\) \( \newcommand\svph{\vphantom{\int}}\) \( \newcommand\vph{\vphantom{\sum_i}}\) \( \newcommand\bvph{\vphantom{\sum_N^N}}\) \( \newcommand\nd{^{\vphantom{\dagger}}}\) \( \newcommand\ns{^{\vphantom{*}}}\) \( \newcommand\yd{^\dagger}\) \( \newcommand\zb{\bar z}\) \( \newcommand\zdot{\dot z}\) \( \newcommand\zbdot{\dot{\bar z}}\) \( \newcommand\kB{k_{\sss{B}}}\) \( \newcommand\kT{k_{\sss{B}}T}\) \( \newcommand\gtau{g_\tau}\) \( \newcommand\Htil{\tilde H}\) \( \newcommand\pairo{(\phi\nd_0,J\nd_0)}\) \( \newcommand\pairm{(\phi\nd_0,J)}\) \( \newcommand\pairob{(\Bphi\nd_0,\BJ\nd_0)}\) \( \newcommand\pairmb{(\Bphi\nd_0,\BJ)}\) \( \newcommand\pair{(\phi,J)}\) \( \newcommand\Hz{H\nd_0}\) \( \newcommand\Ho{H\nd_1}\) \( \newcommand\Htz{\Htil\nd_0}\) \( \newcommand\Hto{\Htil\nd_1}\) \( \newcommand\oc{\omega_\Rc}\)

\(\newcommand \gtwid{\approx}\)

\( \newcommand\index{\textsf{ind}}\) \( \newcommand\csch{\,{ csch\,}}\) \( \newcommand\ctnh{\,{ ctnh\,}}\) \( \newcommand\ctn{\,{ ctn\,}}\) \( \newcommand\sgn{\,{ sgn\,}}\) \( \def\tmapright#1{\xrightarrow \limits^{#1}}\) \( \def\bmapright#1{\xrightarrow\limits_{#1}}\) \( \newcommand\hfb{\hfill\break}\) \( \newcommand\Rep{\textsf{Re}\,}\) \( \newcommand\Imp{\textsf{Im}\,}\) \( \newcommand\ncdot{\!\cdot\!}\) \( \def\tmapright#1{ \smash{\mathop{\hbox to 35pt{\rightarrowfill}}\limits^{#1}}\ }\) \( \def\bmapright#1{ \smash{\mathop{\hbox to 35pt{\rightarrowfill}}\limits_{#1}}\ }\) \( \newcommand\bsqcap{\mbox{\boldmath{$\sqcap$}}}\)

The ordinary canonical partition function for the ideal gas was computed in Equation [ zideal ] . We found

\[\begin{split} Z(T,V,N)&={1\over N!}\prod_{i=1}^N\int\!{d^d\!x\ns_i\, d^d\!p\ns_i\over (2\pi\hbar)^d}\>e^{-\beta\Bp_i^2/2m}\\ &={V^N\over N!}\left(\int\limits_{-\infty}^\infty\!\!{dp\over 2\pi\hbar}\>e^{-\beta p^2/2m}\right)^{\!\!Nd}\\ &={1\over N!}\bigg({V\over\lambda_T^d}\bigg)^{\!N}\ , \end{split}\]

where \(\lambda\ns_T\) is the thermal wavelength :

\[\lambda\ns_T=\sqrt{2\pi\hbar^2/m\kT}\ .\]

The physical interpretation of \(\lambda\ns_T\) is that it is the de Broglie wavelength for a particle of mass \(m\) which has a kinetic energy of \(\kT\).

In the GCE, we have

\[\begin{split} \Xi(T,V,\mu)&=\sum_{N=0}^\infty e^{\beta\mu N}\,Z(T,V,N)\\ &=\sum_{N=1}^\infty {1\over N!}\Bigg({V e^{\mu/\kT}\over \lambda_T^d}\Bigg)^{\!\!N} =\exp\Bigg({V e^{\mu/\kT}\over \lambda_T^d}\Bigg)\ . \end{split}\]

From \(\Xi=e^{-\Omega/\kT}\), we have the grand potential is

\[\Omega(T,V,\mu)=-V\kT\,e^{\mu/\kT}\big/\lambda_T^d\ .\]

Since \(\Omega=-pV\) (see § 6.2 ), we have

\[p(T,\mu)=\kT\,\lambda_T^{-d}\,e^{\mu/\kT}\ .\]

The number density can also be calculated:

\[n={N\over V}=-{1\over V}\pabc{\Omega}{\mu}{T,V}=\lambda_T^{-d}\,e^{\mu/\kT}\ .\]

Combined, the last two equations recapitulate the ideal gas law, \(pV=N\kT\).

Maxwell velocity distribution

The distribution function for momenta is given by

\[g(\Bp)=\Big\langle {1\over N}\sum_{i=1}^N\delta(\Bp\ns_i-\Bp)\Big\rangle\ .\]

Note that \(g(\Bp)=\big\langle\delta(\Bp\ns_i-\Bp)\big\rangle\) is the same for every particle, independent of its label \(i\). We compute the average \(\langle A\rangle=\Tra \big(A e^{-\beta\HH}\big)/\Tra e^{-\beta\HH}\). Setting \(i=1\), all the integrals other than that over \(\Bp\ns_1\) divide out between numerator and denominator. We then have

\[\begin{split} g(\Bp)&={\int\!\!d^3\!p\ns_1 \>\delta(\Bp\ns_1-\Bp)\,e^{-\beta\Bp_1^2/2m}\over \int\!\!d^3\!p\ns_1 \>e^{-\beta\Bp_1^2/2m}}\\ &=(2\pi m\kT)^{-3/2}\,e^{-\beta\Bp^2/2m}\ . \end{split}\]

Textbooks commonly refer to the velocity distribution \(f(\Bv)\), which is related to \(g(\Bp)\) by

\[f(\Bv)\,d^3\!v = g(\Bp)\,d^3\!p\ .\]

\[f(\Bv)=\bigg({m\over 2\pi\kT}\bigg)^{\!3/2}\,e^{-m\Bv^2/2\kT}\ .\]

This is known as the Maxwell velocity distribution . Note that the distributions are normalized, viz.

\[\int\!\!d^3\!p\>g(\Bp)=\int\!\!d^3\!v\,f(\Bv)=1\ .\]

If we are only interested in averaging functions of \(v=|\Bv|\) which are isotropic, then we can define the Maxwell speed distribution , \(\ftil(v)\), as

\[\ftil(v)=4\pi\,v^2 f(\Bv)=4\pi\bigg({m\over 2\pi\kT}\bigg)^{\!3/2}\, v^2\,e^{-mv^2/2\kT}\ .\]

Note that \(\ftil(v)\) is normalized according to

\[\int\limits_0^\infty\!\!dv\,\ftil(v)=1\ .\]

It is convenient to represent \(v\) in units of \(v\ns_0=\sqrt{\kT/m}\), in which case

\[\ftil(v)={1\over v\ns_0}\>\varphi(v/v\ns_0)\qquad,\qquad \varphi(s)=\sqrt{\frac{2}{\pi}}\,s^2\,e^{-s^2/2}\ .\]

The distribution \(\varphi(s)\) is shown in Figure \(\PageIndex{1}\). Computing averages, we have

\[C\ns_k\equiv \langle s^k\rangle=\int\limits_0^\infty\!\! ds\>s^k\,\varphi(s) = 2^{k/2}\cdot {2\over\sqrt{\pi}}\,\RGamma\left(\frac{3}{2} + \frac{k}{2}\right)\ .\]

Thus, \(C\ns_0=1\), \(C\ns_1=\sqrt{\frac{8}{\pi}}\), \(C\ns_2=3\), The speed averages are

\[\blangle v^k\brangle =C\ns_k\,\bigg({\kT\over m}\bigg)^{\!k/2}\ .\]

Note that the average velocity is \(\langle\Bv\rangle=0\), but the average speed is \(\langle v\rangle=\sqrt{8\kT/\pi m}\). The speed distribution is plotted in Figure \(\PageIndex{1}\).

Equipartition

The Hamiltonian for ballistic (massive nonrelativistic) particles is quadratic in the individual components of each momentum \(\Bp\ns_i\). There are other cases in which a classical degree of freedom appears quadratically in \(\HH\) as well. For example, an individual normal mode \(\xi\) of a system of coupled oscillators has the Lagrangian

\[L=\half{\dot\xi}^2-\half\,\omega_0^2\,\xi^2\ ,\]

where the dimensions of \(\xi\) are \([\xi]=M^{1/2} L\) by convention. The Hamiltonian for this normal mode is then

\[\HH={p^2\over 2} + \half\, \omega_0^2\,\xi^2\ ,\]

from which we see that both the kinetic as well as potential energy terms enter quadratically into the Hamiltonian. The classical rotational kinetic energy is also quadratic in the angular momentum components.

Let us compute the contribution of a single quadratic degree of freedom in \(\HH\) to the partition function. We’ll call this degree of freedom \(\zeta\) – it may be a position or momentum or angular momentum – and we’ll write its contribution to \(\HH\) as

\[\HH\ns_\zeta=\half K\zeta^2\ ,\]

where \(K\) is some constant. Integrating over \(\zeta\) yields the following factor in the partition function:

\[\int\limits_{-\infty}^\infty\!\!\!d\zeta\>e^{-\beta K\zeta^2/2}= \bigg({2\pi\over K\beta}\bigg)^{\!1/2}\ .\]

The contribution to the Helmholtz free energy is then

\[\RDelta F\ns_\zeta=\half\kT\ln\!\bigg({K\over 2\pi \kT}\bigg)\ ,\]

and therefore the contribution to the internal energy \(E\) is

\[\RDelta E\ns_\zeta={\pz\over\pz\beta}\big(\beta\,\RDelta F\ns_\zeta\big)= {1\over 2\beta}=\half \kT\ .\]

We have thus derived what is commonly called the equipartition theorem of classical statistical mechanics:

We now see why the internal energy of a classical ideal gas with \(f\) degrees of freedom per molecule is \(E=\half f N\kT\), and \(C\ns_V=\half N\kB\). This result also has applications in the theory of solids. The atoms in a solid possess kinetic energy due to their motion, and potential energy due to the spring-like interatomic potentials which tend to keep the atoms in their preferred crystalline positions. Thus, for a three-dimensional crystal, there are six quadratic degrees of freedom (three positions and three momenta) per atom, and the classical energy should be \(E=3N\kT\), and the heat capacity \(C\ns_V=3N\kB\). As we shall see, quantum mechanics modifies this result considerably at temperatures below the highest normal mode (phonon) frequency, but the high temperature limit is given by the classical value \(C\ns_V=3\nu R\) (where \(\nu=N/\NA\) is the number of moles) derived here, known as the Dulong-Petit limit .

gas law assignmnet

All Formats

Resource types, all resource types.

• Rating Count
• Price (Ascending)
• Price (Descending)
• Most Recent

Gas law assignmnet

Gas Laws Assignment 2 - Charles' Law and Avogadro's Law

• Google Docs™

Ideal Gas Laws Assignment

• Easel Activity

GAS LAWS ASSIGNMENT Video Assignment Grade 11 Chemistry Assignment

• Word Document File

Gas Laws Assignment 3 - Combined Gas Law

Gas Laws Assignment 4 - Ideal Gas Law

Gas Laws Assignment

Gas Laws Assignment 1 - Pressure and Boyle's Law

Gas Laws Assignment 1 - Pressure and Boyle’s Law

Gas Laws Printable and Digital Worksheets | Pressure, Volume, Temperature, Moles

Ideal Gas Law practice *SELF GRADING* google sheet for eLearning

• Google Sheets™

Thanksgiving Turkey Color by Number {Matter, Phase Changes, and Gas Laws }

Gas Laws Scavenger Hunt - Chemistry Activity

Gas Laws Test | Chemistry | Google Forms

• Google Forms™

The Ideal Gas Law Google Form | Chemistry |

The Gas Laws Google Form | Chemistry |

Gas Laws Study Guide | Chemistry | Google Forms

The Ideal Gas Law - Reading Passage and x 10 Questions (EDITABLE)

Graphing Gas Laws

Gas Laws Virtual Station Lab (Distance Learning)

Gas Laws Calculation coloring activity | print and digital worksheet

• Google Apps™
• Internet Activities

Gas Law Practice

States of Matter, Phase Changes, & Gas Laws Task Cards & Color By Number

Crash Course Chemistry #11-15 (Ideal Gas Law , Pressures, Real Gases)

Halloween Phases of Matter, Phase Changes, & Gas Laws Color-by-Number

• We're hiring
• Help & FAQ
• Privacy policy
• Student privacy
• Terms of service
• Tell us what you think

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons
• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

6.4: Gas Laws

• Last updated
• Save as PDF
• Page ID 64040

Learning Objectives

• Learn what is meant by the term gas laws .
• Learn and apply Boyle's law.
• Learn and apply Charles's law.

When seventeenth-century scientists began studying the physical properties of gases, they noticed some simple relationships between some of the measurable properties of the gas. Take pressure ( P ) and volume ( V ), for example. Scientists noted that for a given amount of a gas (usually expressed in units of moles [ n ]), if the temperature ( T ) of the gas was kept constant, pressure and volume were related: As one increases, the other decreases. As one decreases, the other increases. We say that pressure and volume are inversely related .

There is more to it, however: pressure and volume of a given amount of gas at constant temperature are numerically related. If you take the pressure value and multiply it by the volume value, the product is a constant for a given amount of gas at a constant temperature:

P × V = constant at constant n and T

If either volume or pressure changes while amount and temperature stay the same, then the other property must change so that the product of the two properties still equals that same constant. That is, if the original conditions are labeled P 1 and V 1 and the new conditions are labeled P 2 and V 2 , we have

P 1 V 1 = constant = P 2 V 2

where the properties are assumed to be multiplied together. Leaving out the middle part, we have simply

P 1 V 1 = P 2 V 2 at constant n and T

This equation is an example of a gas law. A gas law is a simple mathematical formula that allows you to model, or predict, the behavior of a gas. This particular gas law is called Boyle's law , after the English scientist Robert Boyle, who first announced it in 1662. Figure \(\PageIndex{1}\) shows two representations of how Boyle's law works.

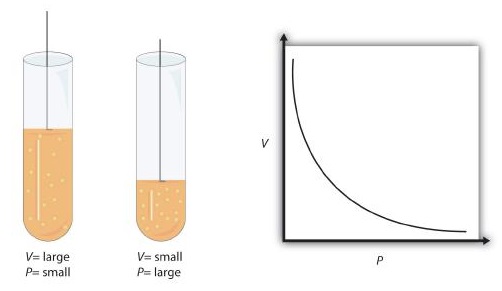
Boyle's law is an example of a second type of mathematical problem we see in chemistry—one based on a mathematical formula. Tactics for working with mathematical formulas are different from tactics for working with conversion factors. First, most of the questions you will have to answer using formulas are word-type questions, so the first step is to identify what quantities are known and assign them to variables. Second, in most formulas, some mathematical rearrangements (i.e., algebra) must be performed to solve for an unknown variable. The rule is that to find the value of the unknown variable, you must mathematically isolate the unknown variable by itself and in the numerator of one side of the equation. Finally, units must be consistent. For example, in Boyle's law there are two pressure variables; they must have the same unit. There are also two volume variables; they also must have the same unit. In most cases, it won't matter what the unit is, but the unit must be the same on both sides of the equation.

Example \(\PageIndex{1}\)

A sample of gas has an initial pressure of 2.44 atm and an initial volume of 4.01 L. Its pressure changes to 1.93 atm. What is the new volume if temperature and amount are kept constant?

First, determine what quantities we are given. We are given an initial pressure and an initial volume, so let these values be P 1 and V 1:

P 1 = 2.44 atm and V 1 = 4.01 L

We are given another quantity, final pressure of 1.93 atm, but not a final volume. This final volume is the variable we will solve for.

P 2 = 1.93 atm and V 2 = ? L

Substituting these values into Boyle's law, we get

(2.44 atm)(4.01 L) = (1.93 atm) V 2

To solve for the unknown variable, we isolate it by dividing both sides of the equation by 1.93 atm—both the number and the unit:

\[\frac{(2.44\, atm)(4.01\, L)}{1.93\, atm}=\frac{(1.93\, atm)\, V_{2}}{1.93\, atm}\nonumber \]

Note that, on the left side of the equation, the unit atm is in the numerator and the denominator of the fraction. They cancel algebraically, just as a number would. On the right side, the unit atm and the number 1.93 are in the numerator and the denominator, so the entire quantity cancels:

\[\frac{(2.44\, \cancel{atm})(4.01\, L)}{1.93\, \cancel{atm}}=\frac{(1.93\, \cancel{atm})\, V_{2}}{1.93\, \cancel{atm}}\nonumber \]

What we have left is

\[\frac{(2.44)(4.01\, L)}{1.93}=V_{2}\nonumber \]

Now we simply multiply and divide the numbers together and combine the answer with the \(L\) unit, which is a unit of volume. Doing so, we get \(V_2 = 5.07\, L\)

Does this answer make sense? We know that pressure and volume are inversely related; as one decreases, the other increases. Pressure is decreasing (from 2.44 atm to 1.93 atm), so volume should be increasing to compensate, and it is (from 4.01 L to 5.07 L). So the answer makes sense based on Boyle's law.

Exercise \(\PageIndex{1}\)

If P 1 = 334 torr, V 1 = 37.8 mL, and P 2 = 102 torr, what is V 2 ?

As mentioned, you can use any units for pressure or volume, but both pressures must be expressed in the same units, and both volumes must be expressed in the same units.

Example \(\PageIndex{2}\)

A sample of gas has an initial pressure of 722 torr and an initial volume of 88.8 mL. Its volume changes to 0.663 L. What is the new pressure?

We can still use Boyle's law to answer this, but now the two volume quantities have different units. It does not matter which unit we change, as long as we perform the conversion correctly. Let us change the 0.663 L to milliliters:

\[0.663\, L\times \frac{1000\, ml}{1\, L}=663\, ml\nonumber \]

Now that both volume quantities have the same units, we can substitute into Boyle's law:

\[(722\, torr)(88.8\, ml)=P_{2}(663\, ml)\nonumber \]

\[\frac{(722\, torr)(88.8)\, ml}{(663\, ml)}=P_{2}\nonumber \]

The mL units cancel, and we multiply and divide the numbers to get P 2 = 96.7 torr

The volume is increasing, and the pressure is decreasing, which is as expected for Boyle's law.

Exercise \(\PageIndex{2}\)

If V 1 = 456 mL, P 1 = 308 torr, and P 2 = 1.55 atm, what is V 2 ?

There are other measurable characteristics of a gas. One of them is temperature ( T ). Perhaps one can vary the temperature of a gas sample and note what effect it has on the other properties of the gas. Early scientists did just this, discovering that if the amount of a gas and its pressure are kept constant, then changing the temperature changes the volume ( V ). As temperature increases, volume increases; as temperature decreases, volume decreases. We say that these two characteristics are directly related .

A mathematical relationship between V and T should be possible except for one thought: what temperature scale should we use? We know from Chapter 2 that science uses several possible temperature scales. Experiments show that the volume of a gas is related to its absolute temperature in Kelvin , not its temperature in degrees Celsius . If the temperature of a gas is expressed in kelvins, then experiments show that the ratio of volume to temperature is a constant:

\[\frac{V}{T}=constant\nonumber \]

We can modify this equation as we modified Boyle's law: the initial conditions V 1 and T 1 have a certain value, and the value must be the same when the conditions of the gas are changed to some new conditions V 2 and T 2 , as long as pressure and the amount of the gas remain constant. Thus, we have another gas law:

\[\frac{V_{1}}{T_{1}}=\frac{V_{2}}{T_{2}}\; at\; constant\; P\; and\; n\nonumber \]

This gas law is commonly referred to as Charles's law , after the French scientist Jacques Charles, who performed experiments on gases in the 1780s. The tactics for using this mathematical formula are similar to those for Boyle's law. To determine an unknown quantity, use algebra to isolate the unknown variable by itself and in the numerator; the units of similar variables must be the same. But we add one more tactic: all temperatures must be expressed in the absolute temperature scale (Kelvin). As a reminder, we review the conversion between the absolute temperature scale and the Celsius temperature scale:

K = °C + 273

where K represents the temperature in kelvins, and °C represents the temperature in degrees Celsius.

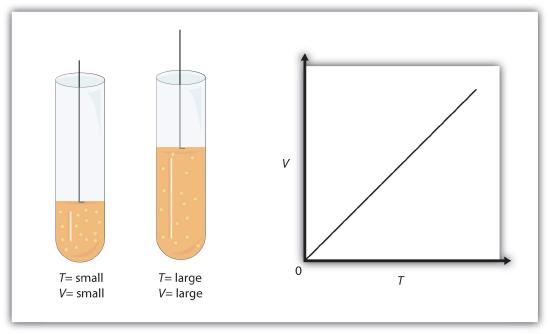
Example \(\PageIndex{3}\)

A sample of gas has an initial volume of 34.8 mL and an initial temperature of 315 K. What is the new volume if the temperature is increased to 559 K? Assume constant pressure and amount for the gas.

First, we assign the given values to their variables. The initial volume is V 1 , so V 1 = 34.8 mL, and the initial temperature is T 1 , so T 1 = 315 K. The temperature is increased to 559 K, so the final temperature T 2 = 559 K. We note that the temperatures are already given in kelvins, so we do not need to convert the temperatures. Substituting into the expression for Charles's law yields

\[\frac{34.8\, ml}{315\, K}=\frac{V_{2}}{559\, K}\nonumber \]

We solve for V 2 by algebraically isolating the V 2 variable on one side of the equation. We do this by multiplying both sides of the equation by 559 K (number and unit). When we do this, the temperature unit cancels on the left side, while the entire 559 K cancels on the right side:

\[\frac{(559\cancel{K})(34.8\, ml)}{315\, \cancel{K}}=\frac{V_{2}(\cancel{559\, K})}{\cancel{559\, K}}\nonumber \]

The expression simplifies to

\[\frac{(559)(34.8\, ml)}{315}=V_{2}\nonumber \]

By multiplying and dividing the numbers, we see that the only remaining unit is mL, so our final answer is

V 2 = 61.8 mL

Does this answer make sense? We know that as temperature increases, volume increases. Here, the temperature is increasing from 315 K to 559 K, so the volume should also increase, which it does.

Exercise \(\PageIndex{3}\)

If V 1 = 3.77 L and T 1 = 255 K, what is V 2 if T 2 = 123 K?

It is more mathematically complicated if a final temperature must be calculated because the T variable is in the denominator of Charles's law. There are several mathematical ways to work this, but perhaps the simplest way is to take the reciprocal of Charles's law. That is, rather than write it as

\[\frac{V_{1}}{T_{1}}=\frac{V_{2}}{T_{2}}\nonumber \]

write the equation as

\[\frac{T_{1}}{V_{1}}=\frac{T_{2}}{V_{2}}\nonumber \]

It is still an equality and a correct form of Charles's law, but now the temperature variable is in the numerator, and the algebra required to predict a final temperature is simpler.

Example \(\PageIndex{4}\)

A sample of a gas has an initial volume of 34.8 L and an initial temperature of −67°C. What must the temperature of the gas be for its volume to be 25.0 L?

Here, we are looking for a final temperature, so we will use the reciprocal form of Charles's law. However, the initial temperature is given in degrees Celsius, not kelvins. We must convert the initial temperature to kelvins:

−67°C + 273 = 206 K

In using the gas law, we must use T 1 = 206 K as the temperature. Substituting into the reciprocal form of Charles's law, we get

\[\frac{206\, K}{34.8\, L}=\frac{T_{2}}{25.0\, L}\nonumber \]

Bringing the 25.0 L quantity over to the other side of the equation, we get

\[\frac{(25.0\cancel{L})(206\, K)}{34.8\cancel{L}}=T_{2}\nonumber \]

The L units cancel, so our final answer is T 2 = 148 K

This is also equal to −125°C. As temperature decreases, volume decreases, which it does in this example.

Exercise \(\PageIndex{4}\)

If V 1 = 623 mL, T 1 = 255°C, and V 2 = 277 mL, what is T 2 ?

235 K, or −38°C

• The behavior of gases can be modeled with gas laws.
• Boyle's law relates a gas's pressure and volume at constant temperature and amount.
• Charles's law relates a gas's volume and temperature at constant pressure and amount.
• In gas laws, temperatures must always be expressed in kelvins.