lesson 3 6 problem solving lines in the coordinate plane

If you're seeing this message, it means we're having trouble loading external resources on our website.

If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.

To log in and use all the features of Khan Academy, please enable JavaScript in your browser.

High school geometry

Course: high school geometry   >   unit 6.

• Area of trapezoid on the coordinate plane

Area & perimeter on the coordinate plane

• Points inside/outside/on a circle
• Challenge problem: Points on two circles
• Coordinate plane word problem
• Coordinate plane word problems: polygons
• (Choice A)   8 ‍   A 8 ‍  
• (Choice B)   9 ‍   B 9 ‍  
• (Choice C)   10 ‍   C 10 ‍  
• (Choice D)   20.8 ‍   D 20.8 ‍  

Problem Solving on the Coordinate Plane

Videos and solutions to help Grade 6 students learn how solve problems related to the distance between points that lie on the same horizontal or vertical line and the coordinate plane.

New York State Common Core Math Module 3, Grade 6, Lessons 19

Students use the coordinate plane to graph points, line segments and geometric shapes in the various quadrants and then use the absolute value to find the related distances.

Opening Exercise

In the coordinate plane, find the distance between the points using absolute value. Exercises

1. Locate and label (4, 5) and 4, –3 ) Draw the line segment between the endpoints given on the coordinate plane. How long is the line segment that you drew? Explain.

2. Draw a horizontal line segment starting at (4, -3) that has a length of units. What are the possible coordinates of the other endpoint of the line segment? (There is more than one answer.)

Which point do you choose to be the other endpoint of the horizontal line segment? Explain how and why you chose that point. Locate and label the point on the coordinate grid.

• Each of the vertices lies in a different quadrant.
• Its sides are either vertical or horizontal.
• The perimeter of the rectangle is 28 units.

Using absolute value, show how the lengths of the sides of your rectangle provide a perimeter of 28 units.

Lesson Summary

The length of a line segment on the coordinate plane can be determined by finding the distance between its endpoints.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.

Choose Your Test

Sat / act prep online guides and tips, coordinate geometry on act math: strategies and practice.

Coordinate geometry is a big focus on the ACT math section, and you’ll need to know its many facets in order to tackle the variety of coordinate geometry questions you’ll see on the test. Luckily, coordinate geometry is not difficult to visualize or wrap your head around once you know the basics. And we are here to walk you through them.

There will usually be three questions on any given ACT that involve points alone, and another two to three questions that will involve lines and slopes and/or rotations, reflections, or translations . These topics are tested by about 10% of your ACT math questions, so it is a good idea to understand the ins and outs of coordinate geometry before you tackle the test.

This article will be your complete guide to points and the building blocks for coordinate geometry: I will explain how to find and manipulate points, distances, and midpoints, and give you strategies for solving these types of questions on the ACT.

What Is Coordinate Geometry?

Geometry always takes place on a plane, which is a flat surface that goes on infinitely in all directions. The coordinate plane refers to a plane that has scales of measurement along the x and y-axes.

Coordinate geometry is the geometry that takes place in the coordinate plane.

Coordinate Scales

The x-axis is the scale that measures horizontal distance along the coordinate plane.

The y-axis is the scale that measures vertical distance along the coordinate plane.

The intersection of the two planes is called the origin .

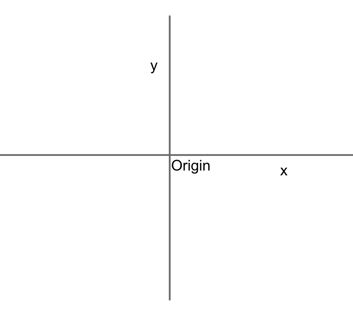
We can find any point along the infinite span of the plane by using its position along the x and y-axes and its distance from the origin. We mark this location with coordinates, written as (x, y).

The x value tells us how far along (and in which direction) our point is along the x-axis.

The y value tells us how far along (and in which direction) our point is along the y-axis.

For instance, take look at the following graph.

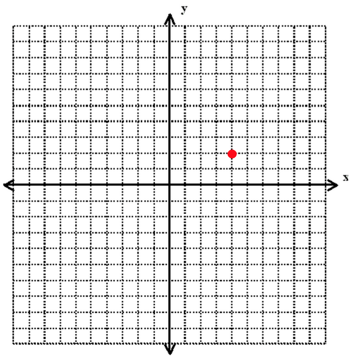
This point is 4 units to the right of the origin and 2 units above the origin. This means that our point is located at coordinates (4, 2).

Anywhere to the right of the origin will have a positive x value . Anywhere left of the origin will have a negative x value .

Anywhere vertically above the origin will have a positive y value . Anywhere vertically below the origin will have a negative y value .

So, if we break up the coordinate plane into four quadrants , we can see that any point will have certain properties in terms of its positivity or negativity, depending on where it is located.

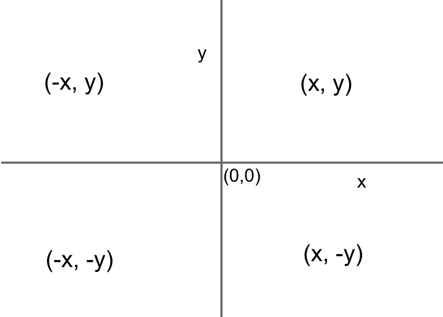
Distances and Midpoints

When given two coordinate points, you can find both the distance between them as well as the midpoint between the two original points. We can find these values by using formulas or by using other geometry techniques.

Let’s breakdown the different ways to solve these types of problems.

Distance Formula

$√{(x_2-x_1)^2+(y_2-y_1)^2}$

There are two options for finding the distance between two points—using the formula, or using the Pythagorean Theorem. Let’s look at both.

Solving Method 1: Distance Formula

If you prefer to use formulas on as many questions as you are able, then go ahead and memorize the distance formula above. You will not be provided any formulas on the ACT math section, including the distance formula, so, if you choose this route, make sure you can memorize the formula accurately and call upon it as needed. (Remember—a formula you remember incorrectly is worse than not knowing a formula at all.)

You will have to memorize each and every ACT math formula you'll need and, for those of you who want to learn as few as possible, the distance formula might be the straw that broke the camel’s back. But for those of you who like formulas and have an easy time memorizing them, adding in the distance formula to your repertoire might not be a problem.

So how do we use our formula in action? Let us say we have two points, (-5, 3) and (1, -5), and we must find the distance between the two.

If we simply plug our values into our distance formula, we get:

$√{(1-(-5))^2+(-5-3)^2}$

$√{(6)^2+(-8)^2}$

$√{(36+64)}$

The distance between our two points is 10.

Solving Method 2: Pythagorean Theorem

$a^2+b^2=c^2$

Alternatively, we can always find the distance between two points by using the Pythagorean Theorem. Though, again, you won’t be given any formulas on the ACT math section, you will need to know the Pythagorean Theorem for many different types of questions, and it's a formula you’ve probably had experience using in your math classes in school. This means you will both need to know it for the test anyway, and you probably already do.

So why can we use the Pythagorean Theorem to find the distance between points? Because the distance formula is actually derived from the Pythagorean Theorem (and we'll show you how in just a bit). The trade-off is that solving your distance questions this way takes slightly longer, but it also doesn’t require you to expend energy memorizing any more formulas than you absolutely need to and carries less risk of remembering the distance formula wrong .

To use the Pythagorean Theorem to find a distance, simply turn the coordinate points and the distance between them into a right triangle, with the distance acting as a hypotenuse. From the coordinates, we can find the lengths of the legs of the triangle and use the Pythagorean Theorem to find our distance.

For example, let us use the same coordinates from earlier to find the distance between them using this method instead.

Find the distance between the points $(−5,3)$ and $(1,−5)$.

First, start by mapping out your coordinates.

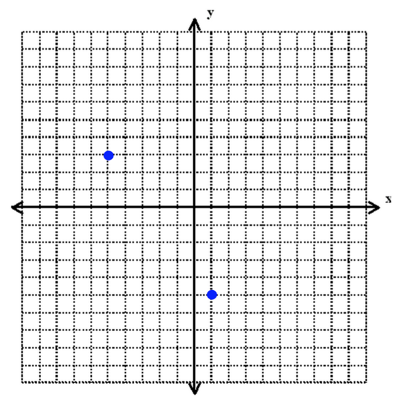
Next, make the legs of your right triangles.

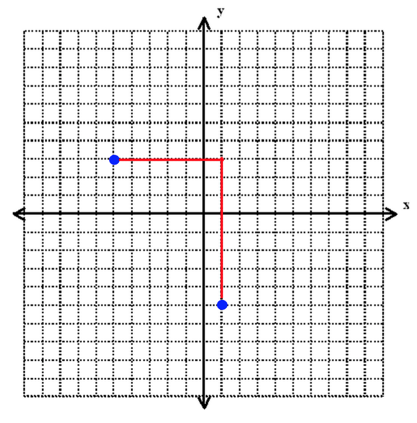
If we count the points along our plane, we can see that we have leg lengths of 6 and 8. Now we can plug these numbers in and use the Pythagorean Theorem to find the final piece of our triangle, the distance between our two points.

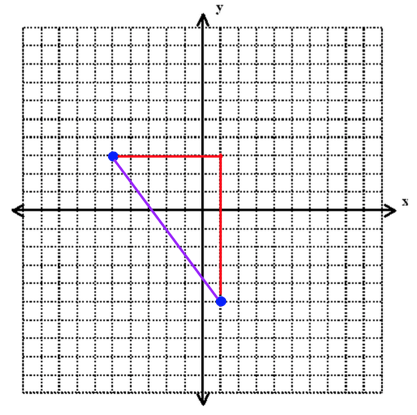
$6^2+8^2=c^2$

$36+64=c^2$

The distance between our two points is, once again, 10.

[Special Note: If you are familiar with your triangle shortcuts , you may have noticed that this triangle was what we call a 3-4-5 triangle multiplied by 2. Because it is one of the regular right triangles, you technically don’t even need the Pythagorean Theorem to know that the hypotenuse will be 10 if the two legs are 6 and 8. This is a shortcut that can be useful to know, but is not necessary to know, as you can see.]

Midpoint Formula

$({{x_1+x_2}/2}$ , ${{y_1+y_2}/2})$

In addition to finding the distance between two points, we can also find the midpoint between two coordinate points. Because this will be another point on the plane, it will have its own set of coordinates.

If you look at the formula, you can see that the midpoint is the average of each of the values of a particular axis. So the midpoint will always be the average of the x values and the average of the y values, written as a coordinate point.

For example, let us take the same points we used for our distance formula, (-5, 3) and (1, -5).

If we take the average of our x values, we get:

And if we take the average of our y values, we get:

${3+(-5)}/2$

The midpoint of the line will be at coordinates (−2,−1).

If we look at our picture from earlier, we can see that this calculation makes sense.

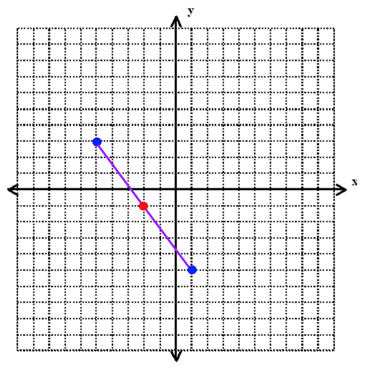
It is difficult to find the midpoint of a line without use of the formula, but thinking of it as finding the average of each axis value, rather than thinking of it as a formal formula, may make it easier to visualize and remember.

Typical Point Questions

Point questions on the ACT will generally fall into one of two categories: questions about how the coordinate plane works and midpoint or distance questions.

Let’s look at each type.

Coordinate Plane Questions

Questions about the coordinate plane test how well you understand exactly how the coordinate plane works, as well as how to manipulate points and lines within it. This can take the form of testing whether or not you understand that the coordinate plane spans infinitely, or how well you understand how negative and positive x and y coordinate values will be, or how well you can visualize points and how they move within the coordinate plane.

Let's take a look at an example:

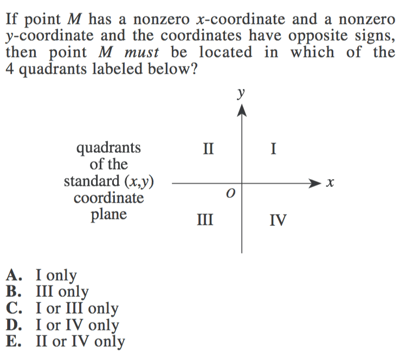
We know from our earlier chart that if x is positive and y is negative, then we will be in quadrant IV, and if x is negative and y is positive, we will be in quadrant II.

Quadrant I will always have both positive x values and positive y values, and quadrant III will always have both negative x values and negative y values. These do not fit our criteria, so we can eliminate them.

This means that our final answer is E , II or IV only.

Midpoint and Distance Questions

Midpoint and distance questions will be fairly straightforward and ask you for exactly that—the distance or the midpoint between two points. You may have to find distances or midpoints from a scenario question (a hypothetical situation or a story) or simply from a straightforward math question (e.g., “What is the distance from points (3, -5) and (4, 4)?”).

Let’s look at an example of a scenario question,

Becky, Lia, and Marian are friends who all live in the same neighborhood. Becky lives 5 miles north of Lia, and Marian lives 12 miles east of Lia. How many miles away do Becky and Marian live from each other?

First, let's make a quick sketch of our scenario.

Now, because this is a distance question, we have the option of using either our distance formula or using the Pythagorean Theorem. Since we have already begun by drawing out our diagram, let's continue on this path and simply use the Pythagorean theorem.

Now, we can see that we have made a right triangle from the legs of distance we have already.

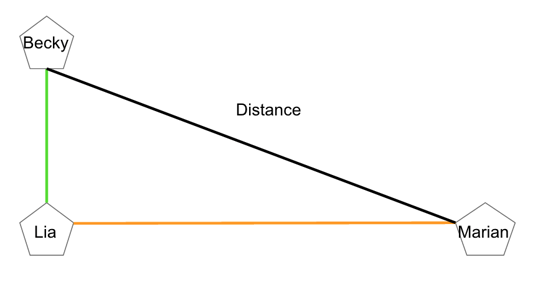
Becky lives 5 miles north and Marian lives 12 miles east, which means that the legs of our triangle will be 5 and 12. Now we can find the hypotenuse by using the Pythagorean theorem.

$5^2+12^2=c^2$

$25+144=c^2$

[Note: if you remember your shortcuts for right triangles , you could have saved yourself some time and simply known that our distance/hypotenuse was 13. Why? Because a right triangle with legs of 5 and 12 means we have a 5-12-13 triangle, which means that the hypotenuse will always be 13.]

The distance between Becky’s house and Marian’s house is 13 miles.

Our final answer is C , 13 miles.

On very rare occasions, you may also be asked for something slightly more peculiar on a midpoint or distance formula, such as the product or the sum of the coordinates. This just requires that you take an extra step once you’ve found your new coordinate points, so don’t get thrown by this scenario.

We know that our midpoints are the averages of our individual coordinates. This means we can work backwards from our one pair of given coordinates and from our midpoint coordinates to find our second pair of original coordinates.

Our first set of original coordinates is at (1,−5), so these will act as our $x_1$ and our $y_1$. And we are told that our midpoint is at (4,−3), so let us set up the problem.

First, let us find the value of our $x_2$ (the x-coordinate of point B).

${x_1+x_2}/2=4$

${1+x_2}/2=4$

Second, let us find the value of our $y_2$ (the y-coordinate of point B).

${y_1+y_2}/2=−3$

${-5-y_2}/2=-3$

$−5+y_2=−6$

Now we just need to add our two coordinates.

Our final answer is C , 6.

ACT Math Strategies for Solving Point Questions

Though point questions can come in a variety of forms, there are a few strategies you can follow to help master them.

#1: Always Write Down Your Given Information

Though it may be tempting to work through questions in your head, it is easy to make mistakes with your point questions if you do not write down your given information. This is especially the case when working with negatives or with absolute values.

In addition, most of the time when you are given a diagram with marked points on the coordinate plane, you will not be given coordinates. This is because the test makers feel it would be too simple a problem to solve had you been given coordinates. So take a moment to write down your coordinates and any other given information in order to keep it straight in your head.

#2: Draw It Out

In addition to writing down your given information, draw pictures of your scenarios. Make your own pictures if you are given none, draw on top of them if you are given diagrams. Never underestimate the value of marking information on a sketch—even a rough approximation can help you keep track of more information than you can (or should try to) in your head.

Time and energy are two precious resources at your disposal when taking the ACT and it takes little of each to make a rough sketch, but can cost you a lot more of both to keep all your information in your head.

#3: Decide Now Which Formulas You Want to Use

If you feel more comfortable using a variety of formulas for a variety of scenarios, then go ahead and memorize the distance formula in addition to all your other need-to-know formulas. But just remember that memorizing a formula wrong is worse than not remembering it at all, so make sure that you memorize and practice all your formula knowledge between now and test day so you can lock it in your head.

If, however, you are someone who prefers to dedicate your study efforts elsewhere (or you simply feel that you won’t remember more than a handful of formulas correctly on the day of the test), then go ahead and forget all your “optional” formulas. Take the time to memorize and use the Pythagorean theorem instead (since you’ll need to know it for a multitude of other types of problems anyway) and wash your hands of the rest of them.

You’ll have to know at least a few formulas to do well on the ACT, but you can absolutely get by with only needing a handful, rather than needing to know them all.

Test (about to be) in progress.

Test Your Knowledge

Now, let’s test your point knowledge on a few more real ACT math questions.

1. In the standard $(x,y)$ coordinate plane, a line segment has its endpoints at $(3,6)$ and $(9,4)$. What are the coordinates of the midpoint of the line segment?

A. $(3,-1)$ B. $(3,1)$ C. $(6,2)$ D. $(6,5)$ E. $(12,10)$

4. What is the distance between coordinates $(4, -2)$ and $(-4, -6)$?

A. $4√5$ B. $5√3$ C. 8 D. $9√3$ E. 14

Answers: D, G, F, A

Answer Explanations:

1. Here, we have a simple midpoint question, so we just need to find the averages of our coordinates.

We are given $(3,6)$ and $(9,4)$, so let us first find the midpoint $x$-coordinate.

$${3+9}/2=12/2=6$$

We know our answer must be C or D, since those are the only options that gives us our midpoint $x$-coordinate at 6. Now let us find our $y$-coordinate.

$${6+4}/2=10/2=5$$

Our midpoint coordinates will be at (6,5).

Our final answer is D, (6,5)

2. If we make a right triangle between the points we are given, we can see that it will have leg lengths of 8 and 8.

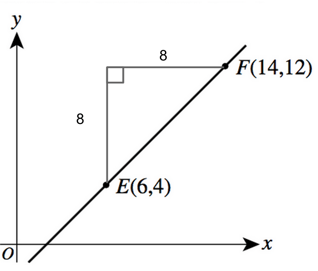
Because the distance will be in proportion to the legs and the distance between E and D is $1/4$ the distance between E and F, we can take $1/4$ of the distance of each leg.

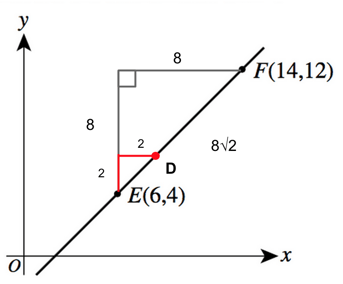
So if we count 2 up from the $x$-coordinate and 2 up from the $y$-coordinate, we get a new coordinate point at (8,6).

Our final answer is G , (8,6).

3. This is a question that may appear at first to be a beast to solve, but the principle behind it is not as complex as it looks. Once we've parsed the text, we can see that we are essentially just being asked to find the square root of the sum of the squares of our coordinate values ($√{x^2+y^2}$).

The easiest way for us to do this is to plug in our own estimated values for our $z$ points. Because we are not given exact coordinate points, we know we will be able to solve the problem without exact coordinates, which means that a rough estimate will do just fine.

So let's give each coordinate point a rough value and say that they are:

$z_1=(−5,6$)

$z_2=(−3,1)$

$z_3=(−3,−3)$

$z_4=(3,−2)$

$z_5=(5,2)$

Now we need to find the square root of the sum of the squares of our coordinate values ($√{x^2+y^2}$).

This means that the squares will cancel out any negative coordinate values (because a negative times a negative is a positive). So we are just looking for whichever $z$ coordinate has the largest absolute value of its coordinates, and these would be $z_5$ and $z_1$. It looks as though $z_1$ will have the largest modulus value, but let's test them both just to be sure.

$√{x^2+y^2}$

$√{5^2+2^2}$

$√{(−5)^2+6^2}$

The point with the greatest modulus value is $z_1$.

Our final answer is F , $z_1$

4. This is a typical distance question and we can, as always, either use the Pythagorean Theorem or the distance formula. In this case, let's just use the distance formula.

$√{(x_2−x_1)^2+(y_2−y_1)^2}$

Our coordinates are: (4,−2) and (−4,−6), so let's plug that into our formula.

$√{((−4)−4)^2+((−6)−(−2))^2}$

$√{(−8)^2+(−4)^2}$

(To understand how to reduce roots like this, check out our guide to advanced integers .)

Our final answer is A , $4√5$

The Take-Aways

The basic building blocks for coordinate geometry are understanding how the coordinate plane works and how points fit in and can be manipulated in it. Once you've grasped these fundamental concepts, you'll be able to perform more complex coordinate geometry tasks, such as finding slopes and rotating shapes .

Coordinate geometry is not an insignificant ACT math topic, but luckily success is mostly a matter of organization and diligence. Be careful to keep track of your negatives and all your moving pieces and you’ll be able to dominate those point questions and all the coordinate geometry the ACT can throw at you.

What’s Next?

Want to brush up on any of your other math topics? Check out our individual math guides to get the walk-through on each and every topic on the ACT math test .

Been procrastinating on your ACT studying? Learn how to overcome your desire to procrastinate and make a well-balanced study plan.

Running out of time on the ACT math section? Our guide will help you how to beat the clock and maximize your ACT math score .

Trying to get a perfect score? Check out our guide to getting a perfect 36 on ACT math , written by a perfect-scorer.

Want to improve your ACT score by 4 points?

Check out our best-in-class online ACT prep program . We guarantee your money back if you don't improve your ACT score by 4 points or more.

Our program is entirely online, and it customizes what you study to your strengths and weaknesses . If you liked this Math lesson, you'll love our program. Along with more detailed lessons, you'll get thousands of practice problems organized by individual skills so you learn most effectively. We'll also give you a step-by-step program to follow so you'll never be confused about what to study next.

Check out our 5-day free trial:

{{cta('999536b9-3e8d-43b1-bb4b-469b84affecc')}}

Courtney scored in the 99th percentile on the SAT in high school and went on to graduate from Stanford University with a degree in Cultural and Social Anthropology. She is passionate about bringing education and the tools to succeed to students from all backgrounds and walks of life, as she believes open education is one of the great societal equalizers. She has years of tutoring experience and writes creative works in her free time.

Student and Parent Forum

Our new student and parent forum, at ExpertHub.PrepScholar.com , allow you to interact with your peers and the PrepScholar staff. See how other students and parents are navigating high school, college, and the college admissions process. Ask questions; get answers.

Ask a Question Below

Have any questions about this article or other topics? Ask below and we'll reply!

Improve With Our Famous Guides

• For All Students

The 5 Strategies You Must Be Using to Improve 160+ SAT Points

How to Get a Perfect 1600, by a Perfect Scorer

Series: How to Get 800 on Each SAT Section:

Score 800 on SAT Math

Score 800 on SAT Reading

Score 800 on SAT Writing

Series: How to Get to 600 on Each SAT Section:

Score 600 on SAT Math

Score 600 on SAT Reading

Score 600 on SAT Writing

Free Complete Official SAT Practice Tests

What SAT Target Score Should You Be Aiming For?

15 Strategies to Improve Your SAT Essay

The 5 Strategies You Must Be Using to Improve 4+ ACT Points

How to Get a Perfect 36 ACT, by a Perfect Scorer

Series: How to Get 36 on Each ACT Section:

36 on ACT English

36 on ACT Math

36 on ACT Reading

36 on ACT Science

Series: How to Get to 24 on Each ACT Section:

24 on ACT English

24 on ACT Math

24 on ACT Reading

24 on ACT Science

What ACT target score should you be aiming for?

ACT Vocabulary You Must Know

ACT Writing: 15 Tips to Raise Your Essay Score

How to Get Into Harvard and the Ivy League

How to Get a Perfect 4.0 GPA

How to Write an Amazing College Essay

What Exactly Are Colleges Looking For?

Is the ACT easier than the SAT? A Comprehensive Guide

Should you retake your SAT or ACT?

When should you take the SAT or ACT?

Stay Informed

Get the latest articles and test prep tips!

Looking for Graduate School Test Prep?

Check out our top-rated graduate blogs here:

GRE Online Prep Blog

GMAT Online Prep Blog

TOEFL Online Prep Blog

Holly R. "I am absolutely overjoyed and cannot thank you enough for helping me!”

Skip to Main Content

• My Assessments
• My Curriculum Maps
• Communities
• Workshop Evaluation

Share Suggestion

Using the coordinate plane in problem solving.

• Printer Friendly Version
• Grade Levels 5th Grade
• Related Academic Standards CC.2.3.5.A.1 Graph points in the first quadrant on the coordinate plane and interpret these points when solving real world and mathematical problems.
• Assessment Anchors M05.C-G.1 Graph points on the coordinate plane to solve real-world and mathematical problems.
• Eligible Content M05.C-G.1.1.2 Represent real-world and mathematical problems by plotting points in quadrant I of the coordinate plane and interpret coordinate values of points in the context of the situation.
• Competencies

This lesson teaches students to solve real-world and mathematical problems using the coordinate plane. Students will:

• solve real-world problems by graphing points on the coordinate plane.
• solve mathematical problems by graphing points on the coordinate plane.
• interpret coordinate values of points in the context of a situation.

Essential Questions

• How are spatial relationships, including shape and dimension, used to draw, construct, model, and represent real situations or solve problems?
• How can geometric properties and theorems be used to describe, model, and analyze situations?
• How can the application of the attributes of geometric shapes support mathematical reasoning and problem solving?
• Coordinate Plane: Formed by the intersection of two number lines (called axes) that meet at right angles at their zero points. Used to locate points in the plane or in space by means of two numbers that represent the distance the point is from the horizontal axis and the vertical axis.
• Origin: The point at which the number lines of a coordinate plane intersect. As an ordered pair, the point (0, 0).
• x -Axis: The horizontal number line of a coordinate plane. Used to show horizontal distance.
• x -Coordinate: The first number in an ordered pair, it designates the distance a point is along the horizontal axis.
• y -Axis: The vertical number line of a coordinate plane. Used to show vertical distance.
• y -Coordinate: The second number in an ordered pair, it designates the distance a point is along the vertical axis.

60–90 minutes

Prerequisite Skills

• at least two copies of the First Quadrant worksheet ( M-5-3-2_First Quadrant and KEY.docx ) for each student
• a copy of Activity 2 Key ( M-5-3-2_Activity 2 KEY.docx ) for each student. Once cut apart, each copy of the key is sufficient for three students.

Related Unit and Lesson Plans

• The Coordinate Plane and Coordinate Geometry
• Introducing the Coordinate Plane
• Classifying Figures on the Coordinate Plane

Related Materials & Resources

The possible inclusion of commercial websites below is not an implied endorsement of their products, which are not free, and are not required for this lesson plan.

• Coordinate Graphs as Maps http://www.ixl.com/math/grade-6/coordinate-graphs-as-maps
• Mapping Shipwrecks with the Coordinate Plane (book excerpt) http://books.google.com/books?id=-uJCqyzwq_cC&printsec=frontcover#v=onepage&q&f=false
• Treasure Hunt Coordinate Plane Lesson http://www.schools.manatee.k12.fl.us/581ETAYLOR/edgeportfolio/treasure_hunt_coordinate_plane_lesson_plan.html

Formative Assessment

• Assess the student-created maps at the end of Activity 1 to determine the level of student understanding.

Suggested Instructional Supports

Instructional procedures.

Depending on how long it has been since students worked with the coordinate plane, a brief review, particularly of the order in which ordered pairs are “followed” may be necessary.

Make sure each student has at least one copy of the First Quadrant worksheet ( M-5-3-2_First Quadrant and KEY.docx ), and each student should work with a partner.

“Take one copy of your worksheet. On the topmost coordinate plane on the worksheet, each group is going to design a map following the same instructions. During the activity, I can repeat any instructions you need, but I can’t answer any other questions. You can talk with your partner about what to do but not to any other groups.”

Read the following instructions, providing time after each instruction for students to complete the instruction.

“You are designing a map of a town you have never visited. When you get to town, your first stop is a welcome center where they provide information to tourists. This welcome center is a little unusual. They don’t have any maps of the town, but they’ll help you create your own. You’re handed a coordinate plane and a pencil and the worker at the welcome center—that’s me—starts to give you instructions so you’ll be able to find your way around town.”

“Plot a point at (4, 4) and label it Library .”

“Plot a point at (8, 4) and label it School .”

After this instruction, since it is near the beginning of the activity, it may be necessary to walk around and make sure students have correctly followed the two instructions thus far.

“Make a point halfway between the library and the school and label it Park . On the side of your worksheet, write the word Park , and then write the coordinates for the point that represents the park.” (6, 4)

“There is a farm that is 6 units above the park. Make a point to represent the location of the farm. On the side of your worksheet, write the word Farm , and then write the coordinates for the point that represents the farm.” (6, 10)

“There is a road that runs in a straight line from the Farm to the School. Draw a line to represent the road.”

“Start at the farm and travel 3 units to the left and 4 units up. There is a lake at that point. Make a point to represent the location of the lake. On the side of your worksheet, write the word Lake , and then write the coordinates for the point that represents the lake.” (3, 14)

“There is a road that runs in a straight line from the lake to the farm. The road then travels in a straight line from the farm to the school. Draw the two parts of the road using straight lines.”

“Finally, there is a road that runs in a straight line from the school to the park. Draw a line to represent the road.”

After students have finished drawing the final road, have each pair of students compare their drawing with that of another group. If their maps differ in any way, the foursome should have you repeat the necessary instructions until the larger group determines which map is correct and fixes the incorrect map.

Make sure all students have the correct map and any misunderstandings in the directions and plotting of points are corrected before continuing.

“In the previous activity, everyone should have ended up with the same map. The directions were specific enough that there was only one possibility for each point. In this activity, you’re going to have a little more freedom to do what you want, but you still have to follow the directions. Start on a new coordinate plane with a point at (8, 8). Label that point Library .”

“The Market is two units away from the Library in any direction you choose. Pick a point that is two units away (left, right, up, or down) from the Library and label the point Market .” Possibilities: (6, 8), (10, 8), (8, 6), (8, 10)

“The Pool is three units away from the Library and is in the opposite direction that you went to make the Market. So, if you put the Market to the left of the Library, where should the Pool go?” ( To the right ) “If you went up, where should the Pool go?” ( Down ) “Go ahead and find the location of the Pool, three units away from the Library. Plot the point and label it Pool .” Possibilities: (11, 8), (5, 8), (8, 5), (8, 11)

“The Arcade has coordinates of 10 and 2, but you can choose the order. You can choose whether the Arcade is at (10, 2) or (2, 10). Go ahead and put the Arcade on your map and label it.”

“City Hall has the same y -coordinate as the Arcade and has an x -coordinate of 7. Go ahead and put City Hall on your map and label it.” (7, 2), (7, 10)

“The last thing to put on your map is the Police Station. The coordinates of the Police Station add up to 12 and one of the coordinates is 5. Go ahead and put the Police Station on your map and label it.” (5, 7), (7, 5)

“Next to your coordinate plane, write the name of each place you graphed and write the coordinates. Remember to put the x -coordinate first and the y -coordinate second.”

Give each student the key for the activity ( M-5-3-2_Activity 2 KEY.docx ) which you have cut into thirds. Have students exchange and check each other’s maps and coordinates to make sure their map is correct.

“Now, each of you should pick a letter from your first or last name—it can be any letter you want—and we’re going to make instructions for someone to follow so s/he can graph the letter you chose. Has everyone chosen a letter?”

Once everyone has chosen a letter, continue: “Decide where you want to start drawing your letter. Remember to think ahead and make sure you have enough space on your coordinate plane to fit the entire letter. Plot the first point in your letter and, on a separate sheet of paper, write down the coordinates of the first point. Now, plot the second point and connect them with a line. Write down the coordinates of the second point underneath the first. Keep plotting points and connecting them, writing them down in order. If you get to somewhere in your letter and you don’t want the new point to be connected to the old one, write the word STOP on your paper before you write down the new point. Once you think you have all the coordinates you need so someone else can graph your letter, double-check your work.”

Once students have listed the coordinates and double-checked their work, they should give their instructions to someone else.

“Now, you have the instructions to make someone else’s letter. Go ahead and start with the first point on the list and graph the points in order. You should always connect each point to the point that came before it unless the instructions contain the word STOP. When you’re finished, compare your letter with your partner and see if your pictures match.”

If the pictures do not match, the pair should work together to either identify where the instructions do not match the original picture or where the second picture does not match the instructions (or both).

This Activity can be repeated if students struggle with writing accurate instructions.

Use the following strategies to tailor the lesson to meet the needs of your students throughout the year.

• Routine: These concepts can be reviewed later in the year using different, more complex maps or having students explore geometric concepts by graphing them on the coordinate plane. For example, once students have learned different classifications of shapes (or parallel / perpendicular lines, etc.) they can create instructions for graphing these geometric items.
• Small Group: Students can work in a small group to create a map of a town and create “clues” to describe the map to another group. Their clues, like the ones in this lesson, can be straightforward (i.e., “The mall is located at (5, 6).”).
• Expansion: This lesson can be expanded by including points outside of Quadrant I as well as including points with decimal coordinates. The maps can always become more complicated, as can the instructions. For example, “The Junior High is located 5 units from the Police Station; plot all the possible locations of the Junior High.”

Related Instructional Videos

• April 15, 2020

Coordinate Planes: Practice Problems

Becoming Familiar with the Coordinate Plane

In this pre-algebra lesson, Juni Mathematics instructor  Genesis  will be teaching you about the coordinate plane and key terms to know.

Coordinate planes are important to understand because they help us know how to read graphs, understand points in space, and even apply concepts in other subjects like  data science  and  coding !

Read Genesis’  Intro to Coordinate Planes lesson  first to understand what coordinate planes are and how to use them. Then, use what you’ve learned with the  warmup questions  on this page to practice drawing coordinate planes and mapping points and lines.

Once you’ve checked your answers below, you can also keep practicing with Genesis’ Drills for Segments in a Coordinate Plane (coming soon).

Warmup Problems

• Draw a coordinate plane that has an x-axis that runs from -6 to 6 and a y-axis that runs from -7 to 7.
• Draw a coordinate plane that has an x-axis that runs from -5 to 5 and a y-axis that also runs from -5 to 5. Then draw a point, A, at the coordinates (-1, 4).
• Draw a coordinate plane that has an x-axis that runs from -3 to 5 and a y-axis that runs from -3 to 5. Then draw a point, B, at the coordinates (3, 2).

Find solutions and Genesis’ tutorial video below!

Solutions Video

Watch Instructor Genesis walk through every problem solution.

Juni Instructor Genesis’ Tutorial:

More Practice for Coordinate Planes

We hope you enjoyed Genesis’ Warmup Problems! Continue practicing coordinate planes with the drills below. Or, review key terms and concepts with Genesis’ Intro to Coordinate Planes lesson and video.

• Intro: Becoming Familiar with Coordinate Planes
• Drills: Segments in a Coordinate Plane (coming soon)

Need help or want to keep learning?

We hope you enjoyed Genesis’ Lesson on Points, Lines, and Coordinate Planes! This lesson falls under our  Pre-Algebra B course curriculum .

To keep practicing or learning, please check out all of our math and coding tutorials on our  Home Learning Resources page .

Need help? Looking up your questions is one of the best ways to learn! Another great way to learn is from an experienced math instructor. From elemenatary math to calculus, Juni offers  online math classes  to accelerate your child’s learning.

Speak with an advisor today about our math classes by calling  (650) 263-4306  or emailing  [email protected] .

Genesis Luna  graduated from the University of Texas at Austin with a B.S.A in Mathematics and a pre-health professions certificate. She is currently a senior instructor at Juni Learning, teaching Python and Mathematics. Genesis enjoys dancing, working on data analysis projects, and cats.

Python Coding Classes for Kids: This Is How to Start

Block Coding for Kids: What Is It and Why Is It Effective?

Coding Projects for Kids: Fun Ways to Get Into Programming

Go further with juni.

Find your potential through our exclusive educational content, guides, and resources only available to Juni Subscribers.

Recent Posts

Looking for a juni course check out our course explorer.

EXPLORE ALL COURSES >>

Get fun activities sent straight to your inbox

Enjoyed this article? Become a Juni subscriber to get even more exclusive educational content, guides, and deals sent straight to your email inbox.

Investing & Entrepreneurship

Communications

Help with Schoolwork

All Courses

How It Works

Instructors

Student Projects

On Demand ACT & SAT Prep

Help Center & FAQ

Founders’ Story

Instructor Jobs

Our Policies

Subscribe to our newsletter

Learn about our latest events, resources, programs, and more!

By subscribing you agree with our Terms of Use & Privacy Policy .

2261 Market St #4242, San Francisco, CA 94114

[email protected]

Discover more from Juni Learning

Subscribe now to keep reading and get access to the full archive.

Type your email…

Continue reading

• Share on Facebook
• Tweet This Resource
• Pin This Resource

Problem Solving and the Coordinate Plane

This problem solving and the coordinate plane lesson plan also includes:.

• Problem Solving and the Coordinate Plane: Teacher Version (.doc)
• Problem Solving and the Coordinate Plane: Student Version (.pdf)
• Problem Solving and the Coordinate Plane: Student Version (.doc)
• Grade 6 Mathematics Module 3: Teacher Materials
• Grade 6 Mathematics Module 3: Student Materials
• Grade 6 Mathematics Module 3: Copy Ready Materials
• Math Fluency Support for Grades 6-8
• Join to access all included materials

Class members investigate rectangles on the coordinate plane. They determine the length of line segments in the coordinate plane with the same x -coordinate or same y -coordinate and then solve geometric problems involving perimeter and area of figures on the coordinate plane.

Additional Tags

Instructional ideas.

• Use the problem set as homework

Classroom Considerations

• Learners should already know how to find distance on the coordinate plane
• 20th installment of a 21-part series
• Scholars need to familiar with perimeter and area of rectangles
• Provides coordinate planes
• Includes sample solutions to all questions

Common Core

Start your free trial.

Save time and discover engaging curriculum for your classroom. Reviewed and rated by trusted, credentialed teachers.

• Collection Types
• Activities & Projects
• Assessments
• Graphics & Images
• Handouts & References
• Interactives
• Lab Resources
• Learning Games
• Lesson Plans
• Presentations
• Primary Sources
• Printables & Templates
• Professional Documents
• Study Guides
• Instructional Videos
• Performance Tasks
• Graphic Organizers
• Writing Prompts
• Constructed Response Items
• AP Test Preps
• Lesson Planet Articles
• Online Courses
• Interactive Whiteboards
• Home Letters
• Unknown Types
• Stock Footages
• All Resource Types

See similar resources:

A five day approach to using technology and manipulatives to explore area and perimeter, area and perimeter: santa style, literal equation application - perimeter of a rectangle (example), khan academy: coordinate plane word problems (quadrant 1 challenging), maximizing and minimizing the area of rectangles given a fixed perimeter, khan academy: coordinate plane word problems (quadrant 1), khan academy: coordinate plane word problems: examples, what is the x-coordinate, how do you use coordinates to translate a figure horizontally.