null and alternative hypothesis of anova

Statistics Made Easy

Understanding the Null Hypothesis for ANOVA Models

A one-way ANOVA is used to determine if there is a statistically significant difference between the mean of three or more independent groups.

A one-way ANOVA uses the following null and alternative hypotheses:

• H 0 :  μ 1  = μ 2  = μ 3  = … = μ k  (all of the group means are equal)
• H A : At least one group mean is different   from the rest

To decide if we should reject or fail to reject the null hypothesis, we must refer to the p-value in the output of the ANOVA table.

If the p-value is less than some significance level (e.g. 0.05) then we can reject the null hypothesis and conclude that not all group means are equal.

A two-way ANOVA is used to determine whether or not there is a statistically significant difference between the means of three or more independent groups that have been split on two variables (sometimes called “factors”).

A two-way ANOVA tests three null hypotheses at the same time:

• All group means are equal at each level of the first variable
• All group means are equal at each level of the second variable
• There is no interaction effect between the two variables

To decide if we should reject or fail to reject each null hypothesis, we must refer to the p-values in the output of the two-way ANOVA table.

The following examples show how to decide to reject or fail to reject the null hypothesis in both a one-way ANOVA and two-way ANOVA.

Example 1: One-Way ANOVA

Suppose we want to know whether or not three different exam prep programs lead to different mean scores on a certain exam. To test this, we recruit 30 students to participate in a study and split them into three groups.

The students in each group are randomly assigned to use one of the three exam prep programs for the next three weeks to prepare for an exam. At the end of the three weeks, all of the students take the same exam. 

The exam scores for each group are shown below:

When we enter these values into the One-Way ANOVA Calculator , we receive the following ANOVA table as the output:

Notice that the p-value is 0.11385 .

For this particular example, we would use the following null and alternative hypotheses:

• H 0 :  μ 1  = μ 2  = μ 3 (the mean exam score for each group is equal)

Since the p-value from the ANOVA table is not less than 0.05, we fail to reject the null hypothesis.

This means we don’t have sufficient evidence to say that there is a statistically significant difference between the mean exam scores of the three groups.

Example 2: Two-Way ANOVA

Suppose a botanist wants to know whether or not plant growth is influenced by sunlight exposure and watering frequency.

She plants 40 seeds and lets them grow for two months under different conditions for sunlight exposure and watering frequency. After two months, she records the height of each plant. The results are shown below:

In the table above, we see that there were five plants grown under each combination of conditions.

For example, there were five plants grown with daily watering and no sunlight and their heights after two months were 4.8 inches, 4.4 inches, 3.2 inches, 3.9 inches, and 4.4 inches:

She performs a two-way ANOVA in Excel and ends up with the following output:

We can see the following p-values in the output of the two-way ANOVA table:

• The p-value for watering frequency is 0.975975 . This is not statistically significant at a significance level of 0.05.
• The p-value for sunlight exposure is 3.9E-8 (0.000000039) . This is statistically significant at a significance level of 0.05.
• The p-value for the interaction between watering  frequency and sunlight exposure is 0.310898 . This is not statistically significant at a significance level of 0.05.

These results indicate that sunlight exposure is the only factor that has a statistically significant effect on plant height.

And because there is no interaction effect, the effect of sunlight exposure is consistent across each level of watering frequency.

That is, whether a plant is watered daily or weekly has no impact on how sunlight exposure affects a plant.

Additional Resources

The following tutorials provide additional information about ANOVA models:

How to Interpret the F-Value and P-Value in ANOVA How to Calculate Sum of Squares in ANOVA What Does a High F Value Mean in ANOVA?

Published by Zach

Leave a reply cancel reply.

Your email address will not be published. Required fields are marked *

Have a thesis expert improve your writing

Check your thesis for plagiarism in 10 minutes, generate your apa citations for free.

• Knowledge Base
• Null and Alternative Hypotheses | Definitions & Examples

Null and Alternative Hypotheses | Definitions & Examples

Published on 5 October 2022 by Shaun Turney . Revised on 6 December 2022.

The null and alternative hypotheses are two competing claims that researchers weigh evidence for and against using a statistical test :

• Null hypothesis (H 0 ): There’s no effect in the population .
• Alternative hypothesis (H A ): There’s an effect in the population.

The effect is usually the effect of the independent variable on the dependent variable .

Table of contents

Answering your research question with hypotheses, what is a null hypothesis, what is an alternative hypothesis, differences between null and alternative hypotheses, how to write null and alternative hypotheses, frequently asked questions about null and alternative hypotheses.

The null and alternative hypotheses offer competing answers to your research question . When the research question asks “Does the independent variable affect the dependent variable?”, the null hypothesis (H 0 ) answers “No, there’s no effect in the population.” On the other hand, the alternative hypothesis (H A ) answers “Yes, there is an effect in the population.”

The null and alternative are always claims about the population. That’s because the goal of hypothesis testing is to make inferences about a population based on a sample . Often, we infer whether there’s an effect in the population by looking at differences between groups or relationships between variables in the sample.

You can use a statistical test to decide whether the evidence favors the null or alternative hypothesis. Each type of statistical test comes with a specific way of phrasing the null and alternative hypothesis. However, the hypotheses can also be phrased in a general way that applies to any test.

The null hypothesis is the claim that there’s no effect in the population.

If the sample provides enough evidence against the claim that there’s no effect in the population ( p ≤ α), then we can reject the null hypothesis . Otherwise, we fail to reject the null hypothesis.

Although “fail to reject” may sound awkward, it’s the only wording that statisticians accept. Be careful not to say you “prove” or “accept” the null hypothesis.

Null hypotheses often include phrases such as “no effect”, “no difference”, or “no relationship”. When written in mathematical terms, they always include an equality (usually =, but sometimes ≥ or ≤).

Examples of null hypotheses

The table below gives examples of research questions and null hypotheses. There’s always more than one way to answer a research question, but these null hypotheses can help you get started.

*Note that some researchers prefer to always write the null hypothesis in terms of “no effect” and “=”. It would be fine to say that daily meditation has no effect on the incidence of depression and p 1 = p 2 .

The alternative hypothesis (H A ) is the other answer to your research question . It claims that there’s an effect in the population.

Often, your alternative hypothesis is the same as your research hypothesis. In other words, it’s the claim that you expect or hope will be true.

The alternative hypothesis is the complement to the null hypothesis. Null and alternative hypotheses are exhaustive, meaning that together they cover every possible outcome. They are also mutually exclusive, meaning that only one can be true at a time.

Alternative hypotheses often include phrases such as “an effect”, “a difference”, or “a relationship”. When alternative hypotheses are written in mathematical terms, they always include an inequality (usually ≠, but sometimes > or <). As with null hypotheses, there are many acceptable ways to phrase an alternative hypothesis.

Examples of alternative hypotheses

The table below gives examples of research questions and alternative hypotheses to help you get started with formulating your own.

Null and alternative hypotheses are similar in some ways:

• They’re both answers to the research question
• They both make claims about the population
• They’re both evaluated by statistical tests.

However, there are important differences between the two types of hypotheses, summarized in the following table.

To help you write your hypotheses, you can use the template sentences below. If you know which statistical test you’re going to use, you can use the test-specific template sentences. Otherwise, you can use the general template sentences.

The only thing you need to know to use these general template sentences are your dependent and independent variables. To write your research question, null hypothesis, and alternative hypothesis, fill in the following sentences with your variables:

Does independent variable affect dependent variable ?

• Null hypothesis (H 0 ): Independent variable does not affect dependent variable .
• Alternative hypothesis (H A ): Independent variable affects dependent variable .

Test-specific

Once you know the statistical test you’ll be using, you can write your hypotheses in a more precise and mathematical way specific to the test you chose. The table below provides template sentences for common statistical tests.

Note: The template sentences above assume that you’re performing one-tailed tests . One-tailed tests are appropriate for most studies.

The null hypothesis is often abbreviated as H 0 . When the null hypothesis is written using mathematical symbols, it always includes an equality symbol (usually =, but sometimes ≥ or ≤).

The alternative hypothesis is often abbreviated as H a or H 1 . When the alternative hypothesis is written using mathematical symbols, it always includes an inequality symbol (usually ≠, but sometimes < or >).

A research hypothesis is your proposed answer to your research question. The research hypothesis usually includes an explanation (‘ x affects y because …’).

A statistical hypothesis, on the other hand, is a mathematical statement about a population parameter. Statistical hypotheses always come in pairs: the null and alternative hypotheses. In a well-designed study , the statistical hypotheses correspond logically to the research hypothesis.

Cite this Scribbr article

If you want to cite this source, you can copy and paste the citation or click the ‘Cite this Scribbr article’ button to automatically add the citation to our free Reference Generator.

Turney, S. (2022, December 06). Null and Alternative Hypotheses | Definitions & Examples. Scribbr. Retrieved 9 April 2024, from https://www.scribbr.co.uk/stats/null-and-alternative-hypothesis/

Is this article helpful?

Shaun Turney

Other students also liked, levels of measurement: nominal, ordinal, interval, ratio, the standard normal distribution | calculator, examples & uses, types of variables in research | definitions & examples.

Understanding the Null Hypothesis for ANOVA Models

A one-way ANOVA is used to determine if there is a statistically significant difference between the mean of three or more independent groups.

A one-way ANOVA uses the following null and alternative hypotheses:

• H 0 :  μ 1  = μ 2  = μ 3  = … = μ k  (all of the group means are equal)
• H A : At least one group mean is different   from the rest

To decide if we should reject or fail to reject the null hypothesis, we must refer to the p-value in the output of the ANOVA table.

If the p-value is less than some significance level (e.g. 0.05) then we can reject the null hypothesis and conclude that not all group means are equal.

A two-way ANOVA is used to determine whether or not there is a statistically significant difference between the means of three or more independent groups that have been split on two variables (sometimes called “factors”).

A two-way ANOVA tests three null hypotheses at the same time:

• All group means are equal at each level of the first variable
• All group means are equal at each level of the second variable
• There is no interaction effect between the two variables

To decide if we should reject or fail to reject each null hypothesis, we must refer to the p-values in the output of the two-way ANOVA table.

The following examples show how to decide to reject or fail to reject the null hypothesis in both a one-way ANOVA and two-way ANOVA.

Example 1: One-Way ANOVA

Suppose we want to know whether or not three different exam prep programs lead to different mean scores on a certain exam. To test this, we recruit 30 students to participate in a study and split them into three groups.

The students in each group are randomly assigned to use one of the three exam prep programs for the next three weeks to prepare for an exam. At the end of the three weeks, all of the students take the same exam. 

The exam scores for each group are shown below:

When we enter these values into the One-Way ANOVA Calculator , we receive the following ANOVA table as the output:

Notice that the p-value is 0.11385 .

For this particular example, we would use the following null and alternative hypotheses:

• H 0 :  μ 1  = μ 2  = μ 3 (the mean exam score for each group is equal)

Since the p-value from the ANOVA table is not less than 0.05, we fail to reject the null hypothesis.

This means we don’t have sufficient evidence to say that there is a statistically significant difference between the mean exam scores of the three groups.

Example 2: Two-Way ANOVA

Suppose a botanist wants to know whether or not plant growth is influenced by sunlight exposure and watering frequency.

She plants 40 seeds and lets them grow for two months under different conditions for sunlight exposure and watering frequency. After two months, she records the height of each plant. The results are shown below:

In the table above, we see that there were five plants grown under each combination of conditions.

For example, there were five plants grown with daily watering and no sunlight and their heights after two months were 4.8 inches, 4.4 inches, 3.2 inches, 3.9 inches, and 4.4 inches:

She performs a two-way ANOVA in Excel and ends up with the following output:

We can see the following p-values in the output of the two-way ANOVA table:

• The p-value for watering frequency is 0.975975 . This is not statistically significant at a significance level of 0.05.
• The p-value for sunlight exposure is 3.9E-8 (0.000000039) . This is statistically significant at a significance level of 0.05.
• The p-value for the interaction between watering  frequency and sunlight exposure is 0.310898 . This is not statistically significant at a significance level of 0.05.

These results indicate that sunlight exposure is the only factor that has a statistically significant effect on plant height.

And because there is no interaction effect, the effect of sunlight exposure is consistent across each level of watering frequency.

That is, whether a plant is watered daily or weekly has no impact on how sunlight exposure affects a plant.

Additional Resources

The following tutorials provide additional information about ANOVA models:

How to Interpret the F-Value and P-Value in ANOVA How to Calculate Sum of Squares in ANOVA What Does a High F Value Mean in ANOVA?

How to Fix in R: incomplete final line found by readTableHeader

Pandas: how to add subtotals to pivot table, related posts, how to normalize data between -1 and 1, vba: how to check if string contains another..., how to interpret f-values in a two-way anova, how to create a vector of ones in..., how to find the mode of a histogram..., how to find quartiles in even and odd..., how to determine if a probability distribution is..., what is a symmetric histogram (definition & examples), how to calculate sxy in statistics (with example), how to calculate sxx in statistics (with example).

Hypothesis Testing - Analysis of Variance (ANOVA)

•   1  
• |   2  
• |   3  
• |   4  
• |   5  

The ANOVA Approach

Test statistic for anova.

All Modules

Table of F-Statistic Values

Consider an example with four independent groups and a continuous outcome measure. The independent groups might be defined by a particular characteristic of the participants such as BMI (e.g., underweight, normal weight, overweight, obese) or by the investigator (e.g., randomizing participants to one of four competing treatments, call them A, B, C and D). Suppose that the outcome is systolic blood pressure, and we wish to test whether there is a statistically significant difference in mean systolic blood pressures among the four groups. The sample data are organized as follows:

The hypotheses of interest in an ANOVA are as follows:

• H 0 : μ 1 = μ 2 = μ 3 ... = μ k
• H 1 : Means are not all equal.

where k = the number of independent comparison groups.

In this example, the hypotheses are:

• H 0 : μ 1 = μ 2 = μ 3 = μ 4
• H 1 : The means are not all equal.

The null hypothesis in ANOVA is always that there is no difference in means. The research or alternative hypothesis is always that the means are not all equal and is usually written in words rather than in mathematical symbols. The research hypothesis captures any difference in means and includes, for example, the situation where all four means are unequal, where one is different from the other three, where two are different, and so on. The alternative hypothesis, as shown above, capture all possible situations other than equality of all means specified in the null hypothesis.

The test statistic for testing H 0 : μ 1 = μ 2 = ... =   μ k is:

and the critical value is found in a table of probability values for the F distribution with (degrees of freedom) df 1 = k-1, df 2 =N-k. The table can be found in "Other Resources" on the left side of the pages.

NOTE: The test statistic F assumes equal variability in the k populations (i.e., the population variances are equal, or s 1 2 = s 2 2 = ... = s k 2 ). This means that the outcome is equally variable in each of the comparison populations. This assumption is the same as that assumed for appropriate use of the test statistic to test equality of two independent means. It is possible to assess the likelihood that the assumption of equal variances is true and the test can be conducted in most statistical computing packages. If the variability in the k comparison groups is not similar, then alternative techniques must be used.

The F statistic is computed by taking the ratio of what is called the "between treatment" variability to the "residual or error" variability. This is where the name of the procedure originates. In analysis of variance we are testing for a difference in means (H 0 : means are all equal versus H 1 : means are not all equal) by evaluating variability in the data. The numerator captures between treatment variability (i.e., differences among the sample means) and the denominator contains an estimate of the variability in the outcome. The test statistic is a measure that allows us to assess whether the differences among the sample means (numerator) are more than would be expected by chance if the null hypothesis is true. Recall in the two independent sample test, the test statistic was computed by taking the ratio of the difference in sample means (numerator) to the variability in the outcome (estimated by Sp).  

The decision rule for the F test in ANOVA is set up in a similar way to decision rules we established for t tests. The decision rule again depends on the level of significance and the degrees of freedom. The F statistic has two degrees of freedom. These are denoted df 1 and df 2 , and called the numerator and denominator degrees of freedom, respectively. The degrees of freedom are defined as follows:

df 1 = k-1 and df 2 =N-k,

where k is the number of comparison groups and N is the total number of observations in the analysis.   If the null hypothesis is true, the between treatment variation (numerator) will not exceed the residual or error variation (denominator) and the F statistic will small. If the null hypothesis is false, then the F statistic will be large. The rejection region for the F test is always in the upper (right-hand) tail of the distribution as shown below.

Rejection Region for F   Test with a =0.05, df 1 =3 and df 2 =36 (k=4, N=40)

For the scenario depicted here, the decision rule is: Reject H 0 if F > 2.87.

return to top | previous page | next page

Content ©2019. All Rights Reserved. Date last modified: January 23, 2019. Wayne W. LaMorte, MD, PhD, MPH

• Privacy Policy

Buy Me a Coffee

Home » ANOVA (Analysis of variance) – Formulas, Types, and Examples

ANOVA (Analysis of variance) – Formulas, Types, and Examples

Table of Contents

Analysis of Variance (ANOVA)

Analysis of Variance (ANOVA) is a statistical method used to test differences between two or more means. It is similar to the t-test, but the t-test is generally used for comparing two means, while ANOVA is used when you have more than two means to compare.

ANOVA is based on comparing the variance (or variation) between the data samples to the variation within each particular sample. If the between-group variance is high and the within-group variance is low, this provides evidence that the means of the groups are significantly different.

ANOVA Terminology

When discussing ANOVA, there are several key terms to understand:

• Factor : This is another term for the independent variable in your analysis. In a one-way ANOVA, there is one factor, while in a two-way ANOVA, there are two factors.
• Levels : These are the different groups or categories within a factor. For example, if the factor is ‘diet’ the levels might be ‘low fat’, ‘medium fat’, and ‘high fat’.
• Response Variable : This is the dependent variable or the outcome that you are measuring.
• Within-group Variance : This is the variance or spread of scores within each level of your factor.
• Between-group Variance : This is the variance or spread of scores between the different levels of your factor.
• Grand Mean : This is the overall mean when you consider all the data together, regardless of the factor level.
• Treatment Sums of Squares (SS) : This represents the between-group variability. It is the sum of the squared differences between the group means and the grand mean.
• Error Sums of Squares (SS) : This represents the within-group variability. It’s the sum of the squared differences between each observation and its group mean.
• Total Sums of Squares (SS) : This is the sum of the Treatment SS and the Error SS. It represents the total variability in the data.
• Degrees of Freedom (df) : The degrees of freedom are the number of values that have the freedom to vary when computing a statistic. For example, if you have ‘n’ observations in one group, then the degrees of freedom for that group is ‘n-1’.
• Mean Square (MS) : Mean Square is the average squared deviation and is calculated by dividing the sum of squares by the corresponding degrees of freedom.
• F-Ratio : This is the test statistic for ANOVAs, and it’s the ratio of the between-group variance to the within-group variance. If the between-group variance is significantly larger than the within-group variance, the F-ratio will be large and likely significant.
• Null Hypothesis (H0) : This is the hypothesis that there is no difference between the group means.
• Alternative Hypothesis (H1) : This is the hypothesis that there is a difference between at least two of the group means.
• p-value : This is the probability of obtaining a test statistic as extreme as the one that was actually observed, assuming that the null hypothesis is true. If the p-value is less than the significance level (usually 0.05), then the null hypothesis is rejected in favor of the alternative hypothesis.
• Post-hoc tests : These are follow-up tests conducted after an ANOVA when the null hypothesis is rejected, to determine which specific groups’ means (levels) are different from each other. Examples include Tukey’s HSD, Scheffe, Bonferroni, among others.

Types of ANOVA

Types of ANOVA are as follows:

One-way (or one-factor) ANOVA

This is the simplest type of ANOVA, which involves one independent variable . For example, comparing the effect of different types of diet (vegetarian, pescatarian, omnivore) on cholesterol level.

Two-way (or two-factor) ANOVA

This involves two independent variables. This allows for testing the effect of each independent variable on the dependent variable , as well as testing if there’s an interaction effect between the independent variables on the dependent variable.

Repeated Measures ANOVA

This is used when the same subjects are measured multiple times under different conditions, or at different points in time. This type of ANOVA is often used in longitudinal studies.

Mixed Design ANOVA

This combines features of both between-subjects (independent groups) and within-subjects (repeated measures) designs. In this model, one factor is a between-subjects variable and the other is a within-subjects variable.

Multivariate Analysis of Variance (MANOVA)

This is used when there are two or more dependent variables. It tests whether changes in the independent variable(s) correspond to changes in the dependent variables.

Analysis of Covariance (ANCOVA)

This combines ANOVA and regression. ANCOVA tests whether certain factors have an effect on the outcome variable after removing the variance for which quantitative covariates (interval variables) account. This allows the comparison of one variable outcome between groups, while statistically controlling for the effect of other continuous variables that are not of primary interest.

Nested ANOVA

This model is used when the groups can be clustered into categories. For example, if you were comparing students’ performance from different classrooms and different schools, “classroom” could be nested within “school.”

ANOVA Formulas

ANOVA Formulas are as follows:

Sum of Squares Total (SST)

This represents the total variability in the data. It is the sum of the squared differences between each observation and the overall mean.

• yi represents each individual data point
• y_mean represents the grand mean (mean of all observations)

Sum of Squares Within (SSW)

This represents the variability within each group or factor level. It is the sum of the squared differences between each observation and its group mean.

• yij represents each individual data point within a group
• y_meani represents the mean of the ith group

Sum of Squares Between (SSB)

This represents the variability between the groups. It is the sum of the squared differences between the group means and the grand mean, multiplied by the number of observations in each group.

• ni represents the number of observations in each group
• y_mean represents the grand mean

Degrees of Freedom

The degrees of freedom are the number of values that have the freedom to vary when calculating a statistic.

For within groups (dfW):

For between groups (dfB):

For total (dfT):

• N represents the total number of observations
• k represents the number of groups

Mean Squares

Mean squares are the sum of squares divided by the respective degrees of freedom.

Mean Squares Between (MSB):

Mean Squares Within (MSW):

F-Statistic

The F-statistic is used to test whether the variability between the groups is significantly greater than the variability within the groups.

If the F-statistic is significantly higher than what would be expected by chance, we reject the null hypothesis that all group means are equal.

Examples of ANOVA

Examples 1:

Suppose a psychologist wants to test the effect of three different types of exercise (yoga, aerobic exercise, and weight training) on stress reduction. The dependent variable is the stress level, which can be measured using a stress rating scale.

Here are hypothetical stress ratings for a group of participants after they followed each of the exercise regimes for a period:

• Yoga: [3, 2, 2, 1, 2, 2, 3, 2, 1, 2]
• Aerobic Exercise: [2, 3, 3, 2, 3, 2, 3, 3, 2, 2]
• Weight Training: [4, 4, 5, 5, 4, 5, 4, 5, 4, 5]

The psychologist wants to determine if there is a statistically significant difference in stress levels between these different types of exercise.

To conduct the ANOVA:

1. State the hypotheses:

• Null Hypothesis (H0): There is no difference in mean stress levels between the three types of exercise.
• Alternative Hypothesis (H1): There is a difference in mean stress levels between at least two of the types of exercise.

2. Calculate the ANOVA statistics:

• Compute the Sum of Squares Between (SSB), Sum of Squares Within (SSW), and Sum of Squares Total (SST).
• Calculate the Degrees of Freedom (dfB, dfW, dfT).
• Calculate the Mean Squares Between (MSB) and Mean Squares Within (MSW).
• Compute the F-statistic (F = MSB / MSW).

3. Check the p-value associated with the calculated F-statistic.

• If the p-value is less than the chosen significance level (often 0.05), then we reject the null hypothesis in favor of the alternative hypothesis. This suggests there is a statistically significant difference in mean stress levels between the three exercise types.

4. Post-hoc tests

• If we reject the null hypothesis, we conduct a post-hoc test to determine which specific groups’ means (exercise types) are different from each other.

Examples 2:

Suppose an agricultural scientist wants to compare the yield of three varieties of wheat. The scientist randomly selects four fields for each variety and plants them. After harvest, the yield from each field is measured in bushels. Here are the hypothetical yields:

The scientist wants to know if the differences in yields are due to the different varieties or just random variation.

Here’s how to apply the one-way ANOVA to this situation:

• Null Hypothesis (H0): The means of the three populations are equal.
• Alternative Hypothesis (H1): At least one population mean is different.
• Calculate the Degrees of Freedom (dfB for between groups, dfW for within groups, dfT for total).
• If the p-value is less than the chosen significance level (often 0.05), then we reject the null hypothesis in favor of the alternative hypothesis. This would suggest there is a statistically significant difference in mean yields among the three varieties.
• If we reject the null hypothesis, we conduct a post-hoc test to determine which specific groups’ means (wheat varieties) are different from each other.

How to Conduct ANOVA

Conducting an Analysis of Variance (ANOVA) involves several steps. Here’s a general guideline on how to perform it:

• Null Hypothesis (H0): The means of all groups are equal.
• Alternative Hypothesis (H1): At least one group mean is different from the others.
• The significance level (often denoted as α) is usually set at 0.05. This implies that you are willing to accept a 5% chance that you are wrong in rejecting the null hypothesis.
• Data should be collected for each group under study. Make sure that the data meet the assumptions of an ANOVA: normality, independence, and homogeneity of variances.
• Calculate the Degrees of Freedom (df) for each sum of squares (dfB, dfW, dfT).
• Compute the Mean Squares Between (MSB) and Mean Squares Within (MSW) by dividing the sum of squares by the corresponding degrees of freedom.
• Compute the F-statistic as the ratio of MSB to MSW.
• Determine the critical F-value from the F-distribution table using dfB and dfW.
• If the calculated F-statistic is greater than the critical F-value, reject the null hypothesis.
• If the p-value associated with the calculated F-statistic is smaller than the significance level (0.05 typically), you reject the null hypothesis.
• If you rejected the null hypothesis, you can conduct post-hoc tests (like Tukey’s HSD) to determine which specific groups’ means (if you have more than two groups) are different from each other.
• Regardless of the result, report your findings in a clear, understandable manner. This typically includes reporting the test statistic, p-value, and whether the null hypothesis was rejected.

When to use ANOVA

ANOVA (Analysis of Variance) is used when you have three or more groups and you want to compare their means to see if they are significantly different from each other. It is a statistical method that is used in a variety of research scenarios. Here are some examples of when you might use ANOVA:

• Comparing Groups : If you want to compare the performance of more than two groups, for example, testing the effectiveness of different teaching methods on student performance.
• Evaluating Interactions : In a two-way or factorial ANOVA, you can test for an interaction effect. This means you are not only interested in the effect of each individual factor, but also whether the effect of one factor depends on the level of another factor.
• Repeated Measures : If you have measured the same subjects under different conditions or at different time points, you can use repeated measures ANOVA to compare the means of these repeated measures while accounting for the correlation between measures from the same subject.
• Experimental Designs : ANOVA is often used in experimental research designs when subjects are randomly assigned to different conditions and the goal is to compare the means of the conditions.

Here are the assumptions that must be met to use ANOVA:

• Normality : The data should be approximately normally distributed.
• Homogeneity of Variances : The variances of the groups you are comparing should be roughly equal. This assumption can be tested using Levene’s test or Bartlett’s test.
• Independence : The observations should be independent of each other. This assumption is met if the data is collected appropriately with no related groups (e.g., twins, matched pairs, repeated measures).

Applications of ANOVA

The Analysis of Variance (ANOVA) is a powerful statistical technique that is used widely across various fields and industries. Here are some of its key applications:

Agriculture

ANOVA is commonly used in agricultural research to compare the effectiveness of different types of fertilizers, crop varieties, or farming methods. For example, an agricultural researcher could use ANOVA to determine if there are significant differences in the yields of several varieties of wheat under the same conditions.

Manufacturing and Quality Control

ANOVA is used to determine if different manufacturing processes or machines produce different levels of product quality. For instance, an engineer might use it to test whether there are differences in the strength of a product based on the machine that produced it.

Marketing Research

Marketers often use ANOVA to test the effectiveness of different advertising strategies. For example, a marketer could use ANOVA to determine whether different marketing messages have a significant impact on consumer purchase intentions.

Healthcare and Medicine

In medical research, ANOVA can be used to compare the effectiveness of different treatments or drugs. For example, a medical researcher could use ANOVA to test whether there are significant differences in recovery times for patients who receive different types of therapy.

ANOVA is used in educational research to compare the effectiveness of different teaching methods or educational interventions. For example, an educator could use it to test whether students perform significantly differently when taught with different teaching methods.

Psychology and Social Sciences

Psychologists and social scientists use ANOVA to compare group means on various psychological and social variables. For example, a psychologist could use it to determine if there are significant differences in stress levels among individuals in different occupations.

Biology and Environmental Sciences

Biologists and environmental scientists use ANOVA to compare different biological and environmental conditions. For example, an environmental scientist could use it to determine if there are significant differences in the levels of a pollutant in different bodies of water.

Advantages of ANOVA

Here are some advantages of using ANOVA:

Comparing Multiple Groups: One of the key advantages of ANOVA is the ability to compare the means of three or more groups. This makes it more powerful and flexible than the t-test, which is limited to comparing only two groups.

Control of Type I Error: When comparing multiple groups, the chances of making a Type I error (false positive) increases. One of the strengths of ANOVA is that it controls the Type I error rate across all comparisons. This is in contrast to performing multiple pairwise t-tests which can inflate the Type I error rate.

Testing Interactions: In factorial ANOVA, you can test not only the main effect of each factor, but also the interaction effect between factors. This can provide valuable insights into how different factors or variables interact with each other.

Handling Continuous and Categorical Variables: ANOVA can handle both continuous and categorical variables . The dependent variable is continuous and the independent variables are categorical.

Robustness: ANOVA is considered robust to violations of normality assumption when group sizes are equal. This means that even if your data do not perfectly meet the normality assumption, you might still get valid results.

Provides Detailed Analysis: ANOVA provides a detailed breakdown of variances and interactions between variables which can be useful in understanding the underlying factors affecting the outcome.

Capability to Handle Complex Experimental Designs: Advanced types of ANOVA (like repeated measures ANOVA, MANOVA, etc.) can handle more complex experimental designs, including those where measurements are taken on the same subjects over time, or when you want to analyze multiple dependent variables at once.

Disadvantages of ANOVA

Some limitations or disadvantages that are important to consider:

Assumptions: ANOVA relies on several assumptions including normality (the data follows a normal distribution), independence (the observations are independent of each other), and homogeneity of variances (the variances of the groups are roughly equal). If these assumptions are violated, the results of the ANOVA may not be valid.

Sensitivity to Outliers: ANOVA can be sensitive to outliers. A single extreme value in one group can affect the sum of squares and consequently influence the F-statistic and the overall result of the test.

Dichotomous Variables: ANOVA is not suitable for dichotomous variables (variables that can take only two values, like yes/no or male/female). It is used to compare the means of groups for a continuous dependent variable.

Lack of Specificity: Although ANOVA can tell you that there is a significant difference between groups, it doesn’t tell you which specific groups are significantly different from each other. You need to carry out further post-hoc tests (like Tukey’s HSD or Bonferroni) for these pairwise comparisons.

Complexity with Multiple Factors: When dealing with multiple factors and interactions in factorial ANOVA, interpretation can become complex. The presence of interaction effects can make main effects difficult to interpret.

Requires Larger Sample Sizes: To detect an effect of a certain size, ANOVA generally requires larger sample sizes than a t-test.

Equal Group Sizes: While not always a strict requirement, ANOVA is most powerful and its assumptions are most likely to be met when groups are of equal or similar sizes.

About the author

Muhammad Hassan

Researcher, Academic Writer, Web developer

You may also like

Cluster Analysis – Types, Methods and Examples

Discriminant Analysis – Methods, Types and...

MANOVA (Multivariate Analysis of Variance) –...

Documentary Analysis – Methods, Applications and...

Graphical Methods – Types, Examples and Guide

Substantive Framework – Types, Methods and...

Have a language expert improve your writing

Run a free plagiarism check in 10 minutes, generate accurate citations for free.

• Knowledge Base

ANOVA in R | A Complete Step-by-Step Guide with Examples

Published on March 6, 2020 by Rebecca Bevans . Revised on June 22, 2023.

ANOVA is a statistical test for estimating how a quantitative dependent variable changes according to the levels of one or more categorical independent variables . ANOVA tests whether there is a difference in means of the groups at each level of the independent variable.

The null hypothesis ( H 0 ) of the ANOVA is no difference in means, and the alternative hypothesis ( H a ) is that the means are different from one another.

In this guide, we will walk you through the process of a one-way ANOVA (one independent variable) and a two-way ANOVA (two independent variables).

Our sample dataset contains observations from an imaginary study of the effects of fertilizer type and planting density on crop yield.

We will also include examples of how to perform and interpret a two-way ANOVA with an interaction term, and an ANOVA with a blocking variable.

Sample dataset for ANOVA

Table of contents

Getting started in r, step 1: load the data into r, step 2: perform the anova test, step 3: find the best-fit model, step 4: check for homoscedasticity, step 5: do a post-hoc test, step 6: plot the results in a graph, step 7: report the results, other interesting articles, frequently asked questions about anova.

If you haven’t used R before, start by downloading R and R Studio . Once you have both of these programs downloaded, open R Studio and click on File > New File > R Script .

Now you can copy and paste the code from the rest of this example into your script. To run the code, highlight the lines you want to run and click on the Run  button on the top right of the text editor (or press ctrl + enter on the keyboard).

Install and load the packages

First, install the packages you will need for the analysis (this only needs to be done once):

Then load these packages into your R environment (do this every time you restart the R program):

Note that this data was generated for this example, it’s not from a real experiment.

We will use the same dataset for all of our examples in this walkthrough. The only difference between the different analyses is how many independent variables we include and in what combination we include them.

It is common for factors to be read as quantitative variables when importing a dataset into R. To avoid this, you can use the read.csv() command to read in the data, specifying within the command whether each of the variables should be quantitative (“numeric”) or categorical (“factor”).

Use the following code, replacing the path/to/your/file text with the actual path to your file:

Before continuing, you can check that the data has read in correctly:

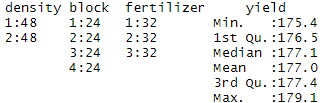
You should see ‘density’, ‘block’, and ‘fertilizer’ listed as categorical variables with the number of observations at each level (i.e. 48 observations at density 1 and 48 observations at density 2).

‘Yield’ should be a quantitative variable with a numeric summary (minimum, median , mean , maximum).

ANOVA tests whether any of the group means are different from the overall mean of the data by checking the variance of each individual group against the overall variance of the data. If one or more groups falls outside the range of variation predicted by the null hypothesis (all group means are equal), then the test is statistically significant .

We can perform an ANOVA in R using the aov() function. This will calculate the test statistic for ANOVA and determine whether there is significant variation among the groups formed by the levels of the independent variable.

One-way ANOVA

In the one-way ANOVA example, we are modeling crop yield as a function of the type of fertilizer used. First we will use aov() to run the model, then we will use summary() to print the summary of the model.

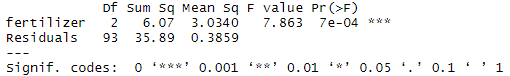
The model summary first lists the independent variables being tested in the model (in this case we have only one, ‘fertilizer’) and the model residuals (‘Residual’). All of the variation that is not explained by the independent variables is called residual variance.

The rest of the values in the output table describe the independent variable and the residuals:

• The Df column displays the degrees of freedom for the independent variable (the number of levels in the variable minus 1), and the degrees of freedom for the residuals (the total number of observations minus one and minus the number of levels in the independent variables).
• The Sum Sq column displays the sum of squares (a.k.a. the total variation between the group means and the overall mean).
• The Mean Sq column is the mean of the sum of squares, calculated by dividing the sum of squares by the degrees of freedom for each parameter.
• The F value column is the test statistic from the F test. This is the mean square of each independent variable divided by the mean square of the residuals. The larger the F value, the more likely it is that the variation caused by the independent variable is real and not due to chance.
• The Pr(>F) column is the p value of the F statistic. This shows how likely it is that the F value calculated from the test would have occurred if the null hypothesis of no difference among group means were true.

The p value of the fertilizer variable is low ( p < 0.001), so it appears that the type of fertilizer used has a real impact on the final crop yield.

Two-way ANOVA

In the two-way ANOVA example, we are modeling crop yield as a function of type of fertilizer and planting density. First we use aov() to run the model, then we use summary() to print the summary of the model.

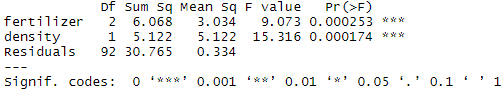
Adding planting density to the model seems to have made the model better: it reduced the residual variance (the residual sum of squares went from 35.89 to 30.765), and both planting density and fertilizer are statistically significant (p-values < 0.001).

Adding interactions between variables

Sometimes you have reason to think that two of your independent variables have an interaction effect rather than an additive effect.

For example, in our crop yield experiment, it is possible that planting density affects the plants’ ability to take up fertilizer. This might influence the effect of fertilizer type in a way that isn’t accounted for in the two-way model.

To test whether two variables have an interaction effect in ANOVA, simply use an asterisk instead of a plus-sign in the model:

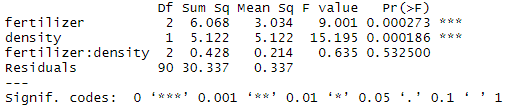
In the output table, the ‘fertilizer:density’ variable has a low sum-of-squares value and a high p value, which means there is not much variation that can be explained by the interaction between fertilizer and planting density.

Adding a blocking variable

If you have grouped your experimental treatments in some way, or if you have a confounding variable that might affect the relationship you are interested in testing, you should include that element in the model as a blocking variable. The simplest way to do this is just to add the variable into the model with a ‘+’.

For example, in many crop yield studies, treatments are applied within ‘blocks’ in the field that may differ in soil texture, moisture, sunlight, etc. To control for the effect of differences among planting blocks we add a third term, ‘block’, to our ANOVA.

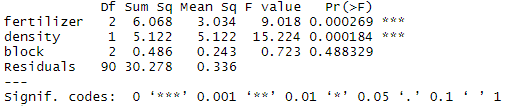
The ‘block’ variable has a low sum-of-squares value (0.486) and a high p value (p = 0.48), so it’s probably not adding much information to the model. It also doesn’t change the sum of squares for the two independent variables, which means that it’s not affecting how much variation in the dependent variable they explain.

There are now four different ANOVA models to explain the data. How do you decide which one to use? Usually you’ll want to use the ‘best-fit’ model – the model that best explains the variation in the dependent variable.

The Akaike information criterion (AIC) is a good test for model fit. AIC calculates the information value of each model by balancing the variation explained against the number of parameters used.

In AIC model selection, we compare the information value of each model and choose the one with the lowest AIC value (a lower number means more information explained!)

The model with the lowest AIC score (listed first in the table) is the best fit for the data:

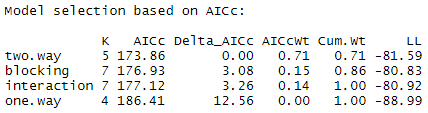
From these results, it appears that the two.way model is the best fit. The two-way model has the lowest AIC value, and 71% of the AIC weight, which means that it explains 71% of the total variation in the dependent variable that can be explained by the full set of models.

The model with blocking term contains an additional 15% of the AIC weight, but because it is more than 2 delta-AIC worse than the best model, it probably isn’t good enough to include in your results.

To check whether the model fits the assumption of homoscedasticity , look at the model diagnostic plots in R using the plot() function:

The output looks like this:

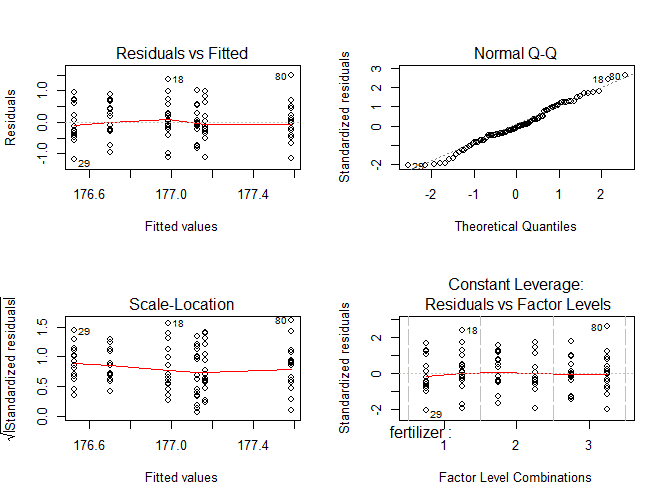
The diagnostic plots show the unexplained variance (residuals) across the range of the observed data.

Each plot gives a specific piece of information about the model fit, but it’s enough to know that the red line representing the mean of the residuals should be horizontal and centered on zero (or on one, in the scale-location plot), meaning that there are no large outliers that would cause research bias in the model.

The normal Q-Q plot plots a regression between the theoretical residuals of a perfectly-homoscedastic model and the actual residuals of your model, so the closer to a slope of 1 this is the better. This Q-Q plot is very close, with only a bit of deviation.

From these diagnostic plots we can say that the model fits the assumption of homoscedasticity.

If your model doesn’t fit the assumption of homoscedasticity, you can try the Kruskall-Wallis test instead.

ANOVA tells us if there are differences among group means, but not what the differences are. To find out which groups are statistically different from one another, you can perform a Tukey’s Honestly Significant Difference (Tukey’s HSD) post-hoc test for pairwise comparisons:

From the post-hoc test results, we see that there are statistically significant differences (p < 0.05) between fertilizer groups 3 and 1 and between fertilizer types 3 and 2, but the difference between fertilizer groups 2 and 1 is not statistically significant. There is also a significant difference between the two different levels of planting density.

When plotting the results of a model, it is important to display:

• the raw data
• summary information, usually the mean and standard error of each group being compared
• letters or symbols above each group being compared to indicate the groupwise differences.

Find the groupwise differences

From the ANOVA test we know that both planting density and fertilizer type are significant variables. To display this information on a graph, we need to show which of the combinations of fertilizer type + planting density are statistically different from one another.

To do this, we can run another ANOVA + TukeyHSD test, this time using the interaction of fertilizer and planting density. We aren’t doing this to find out if the interaction term is significant (we already know it’s not), but rather to find out which group means are statistically different from one another so we can add this information to the graph.

Instead of printing the TukeyHSD results in a table, we’ll do it in a graph.

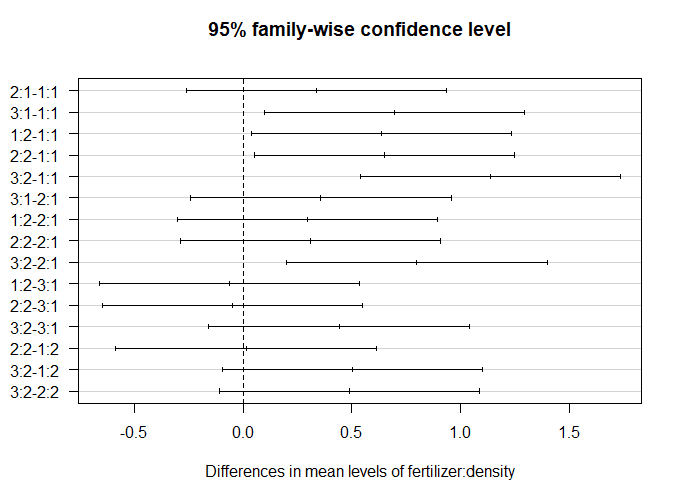
The significant groupwise differences are any where the 95% confidence interval doesn’t include zero. This is another way of saying that the p value for these pairwise differences is < 0.05.

From this graph, we can see that the fertilizer + planting density combinations which are significantly different from one another are 3:1-1:1 (read as “fertilizer type three + planting density 1 contrasted with fertilizer type 1 + planting density type 1”), 1:2-1:1, 2:2-1:1, 3:2-1:1, and 3:2-2:1.

We can make three labels for our graph: A (representing 1:1), B (representing all the intermediate combinations), and C (representing 3:2).

Make a data frame with the group labels

Now we need to make an additional data frame so we can add these groupwise differences to our graph.

First, summarize the original data using fertilizer type and planting density as grouping variables.

Next, add the group labels as a new variable in the data frame.

Your data frame should look like this:

Now we are ready to start making the plot for our report.

Plot the raw data

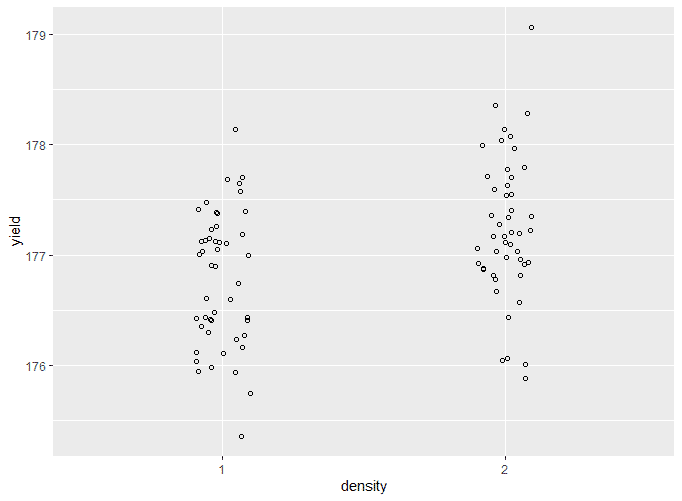
Add the means and standard errors to the graph

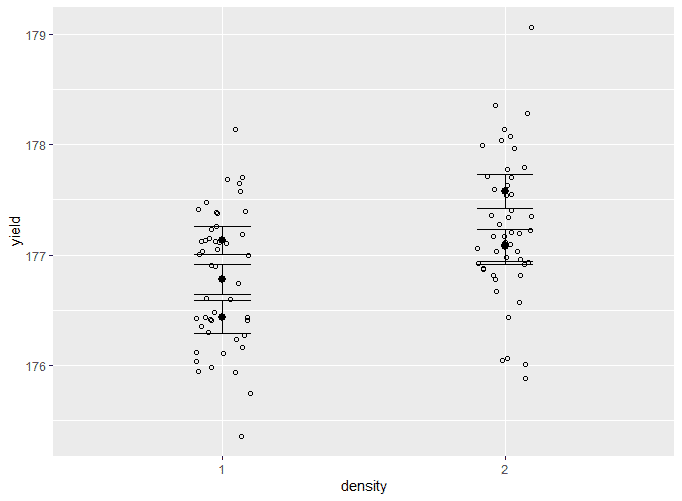
This is very hard to read, since all of the different groupings for fertilizer type are stacked on top of one another. We will solve this in the next step.

Split up the data

To show which groups are different from one another, use facet_wrap() to split the data up over the three types of fertilizer. To add labels, use geom_text() , and add the group letters from the mean.yield.data dataframe you made earlier.

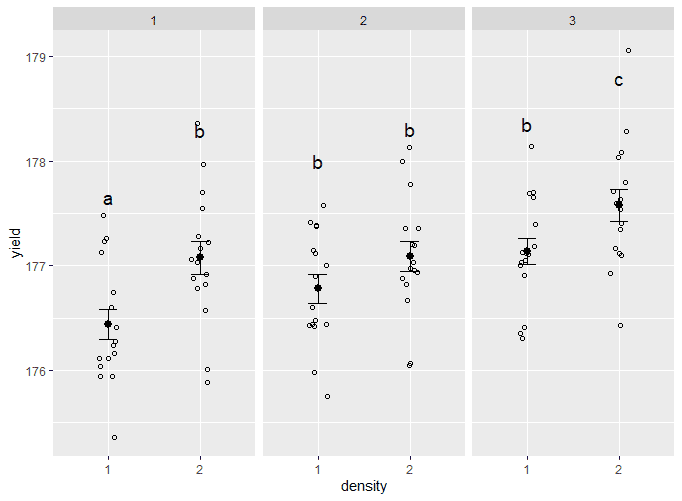
Make the graph ready for publication

In this step we will remove the grey background and add axis labels.

The final version of your graph looks like this:

In addition to a graph, it’s important to state the results of the ANOVA test. Include:

• A brief description of the variables you tested
• The F value, degrees of freedom, and p values for each independent variable
• What the results mean.

A Tukey post-hoc test revealed that fertilizer mix 3 resulted in a higher yield on average than fertilizer mix 1 (0.59 bushels/acre), and a higher yield on average than fertilizer mix 2 (0.42 bushels/acre). Planting density was also significant, with planting density 2 resulting in an higher yield on average of 0.46 bushels/acre over planting density 1.

If you want to know more about statistics , methodology , or research bias , make sure to check out some of our other articles with explanations and examples.

• Chi square test of independence
• Statistical power
• Descriptive statistics
• Degrees of freedom
• Pearson correlation
• Null hypothesis

Methodology

• Double-blind study
• Case-control study
• Research ethics
• Data collection
• Hypothesis testing
• Structured interviews

Research bias

• Hawthorne effect
• Unconscious bias
• Recall bias
• Halo effect
• Self-serving bias
• Information bias

The only difference between one-way and two-way ANOVA is the number of independent variables . A one-way ANOVA has one independent variable, while a two-way ANOVA has two.

• One-way ANOVA : Testing the relationship between shoe brand (Nike, Adidas, Saucony, Hoka) and race finish times in a marathon.
• Two-way ANOVA : Testing the relationship between shoe brand (Nike, Adidas, Saucony, Hoka), runner age group (junior, senior, master’s), and race finishing times in a marathon.

All ANOVAs are designed to test for differences among three or more groups. If you are only testing for a difference between two groups, use a t-test instead.

A factorial ANOVA is any ANOVA that uses more than one categorical independent variable . A two-way ANOVA is a type of factorial ANOVA.

Some examples of factorial ANOVAs include:

• Testing the combined effects of vaccination (vaccinated or not vaccinated) and health status (healthy or pre-existing condition) on the rate of flu infection in a population.
• Testing the effects of marital status (married, single, divorced, widowed), job status (employed, self-employed, unemployed, retired), and family history (no family history, some family history) on the incidence of depression in a population.
• Testing the effects of feed type (type A, B, or C) and barn crowding (not crowded, somewhat crowded, very crowded) on the final weight of chickens in a commercial farming operation.

In ANOVA, the null hypothesis is that there is no difference among group means. If any group differs significantly from the overall group mean, then the ANOVA will report a statistically significant result.

Significant differences among group means are calculated using the F statistic, which is the ratio of the mean sum of squares (the variance explained by the independent variable) to the mean square error (the variance left over).

If the F statistic is higher than the critical value (the value of F that corresponds with your alpha value, usually 0.05), then the difference among groups is deemed statistically significant.

Quantitative variables are any variables where the data represent amounts (e.g. height, weight, or age).

Categorical variables are any variables where the data represent groups. This includes rankings (e.g. finishing places in a race), classifications (e.g. brands of cereal), and binary outcomes (e.g. coin flips).

You need to know what type of variables you are working with to choose the right statistical test for your data and interpret your results .

Cite this Scribbr article

If you want to cite this source, you can copy and paste the citation or click the “Cite this Scribbr article” button to automatically add the citation to our free Citation Generator.

Bevans, R. (2023, June 22). ANOVA in R | A Complete Step-by-Step Guide with Examples. Scribbr. Retrieved April 9, 2024, from https://www.scribbr.com/statistics/anova-in-r/

Is this article helpful?

Rebecca Bevans

Other students also liked, one-way anova | when and how to use it (with examples), two-way anova | examples & when to use it, akaike information criterion | when & how to use it (example), what is your plagiarism score.

Module 13: F-Distribution and One-Way ANOVA

One-way anova, learning outcomes.

• Conduct and interpret one-way ANOVA

The purpose of a one-way ANOVA test is to determine the existence of a statistically significant difference among several group means. The test actually uses variances to help determine if the means are equal or not. In order to perform a one-way ANOVA test, there are five basic assumptions to be fulfilled:

• Each population from which a sample is taken is assumed to be normal.
• All samples are randomly selected and independent.
• The populations are assumed to have equal standard deviations (or variances) .
• The factor is a categorical variable.
• The response is a numerical variable.

The Null and Alternative Hypotheses

The null hypothesis is simply that all the group population means are the same. The alternative hypothesis is that at least one pair of means is different. For example, if there are k groups:

H 0 : μ 1 = μ 2 = μ 3 = … = μ k

H a : At least two of the group means μ 1 , μ 2 , μ 3 , …, μ k are not equal.

The graphs, a set of box plots representing the distribution of values with the group means indicated by a horizontal line through the box, help in the understanding of the hypothesis test. In the first graph (red box plots), H 0 : μ 1 = μ 2 = μ 3 and the three populations have the same distribution if the null hypothesis is true. The variance of the combined data is approximately the same as the variance of each of the populations.

If the null hypothesis is false, then the variance of the combined data is larger which is caused by the different means as shown in the second graph (green box plots).

(b) H 0 is not true. All means are not the same; the differences are too large to be due to random variation.

Concept Review

Analysis of variance extends the comparison of two groups to several, each a level of a categorical variable (factor). Samples from each group are independent, and must be randomly selected from normal populations with equal variances. We test the null hypothesis of equal means of the response in every group versus the alternative hypothesis of one or more group means being different from the others. A one-way ANOVA hypothesis test determines if several population means are equal. The distribution for the test is the F distribution with two different degrees of freedom.

Assumptions:

• The populations are assumed to have equal standard deviations (or variances).
• OpenStax, Statistics, One-Way ANOVA. Located at : http://cnx.org/contents/[email protected] . License : CC BY: Attribution
• Introductory Statistics . Authored by : Barbara Illowski, Susan Dean. Provided by : Open Stax. Located at : http://cnx.org/contents/[email protected] . License : CC BY: Attribution . License Terms : Download for free at http://cnx.org/contents/[email protected]
• Completing a simple ANOVA table. Authored by : masterskills. Located at : https://youtu.be/OXA-bw9tGfo . License : All Rights Reserved . License Terms : Standard YouTube License

13.1 One-Way ANOVA

The purpose of a one-way ANOVA test is to determine the existence of a statistically significant difference among several group means. The test uses variances to help determine if the means are equal or not. To perform a one-way ANOVA test, there are five basic assumptions to be fulfilled:

• Each population from which a sample is taken is assumed to be normal.
• All samples are randomly selected and independent.
• The populations are assumed to have equal standard deviations (or variances).
• The factor is a categorical variable.
• The response is a numerical variable.

The Null and Alternative Hypotheses

The null hypothesis is that all the group population means are the same. The alternative hypothesis is that at least one pair of means is different. For example, if there are k groups

H 0 : μ 1 = μ 2 = μ 3 = ... = μ k

H a : At least two of the group means μ 1 , μ 2 , μ 3 , ..., μ k are not equal. That is, μ i ≠ μ j for some i ≠ j .

The graphs, a set of box plots representing the distribution of values with the group means indicated by a horizontal line through the box, help in the understanding of the hypothesis test. In the first graph (red box plots), H 0 : μ 1 = μ 2 = μ 3 and the three populations have the same distribution if the null hypothesis is true. The variance of the combined data is approximately the same as the variance of each of the populations.

If the null hypothesis is false, then the variance of the combined data is larger, which is caused by the different means as shown in the second graph (green box plots).

As an Amazon Associate we earn from qualifying purchases.

This book may not be used in the training of large language models or otherwise be ingested into large language models or generative AI offerings without OpenStax's permission.

Want to cite, share, or modify this book? This book uses the Creative Commons Attribution License and you must attribute Texas Education Agency (TEA). The original material is available at: https://www.texasgateway.org/book/tea-statistics . Changes were made to the original material, including updates to art, structure, and other content updates.

Access for free at https://openstax.org/books/statistics/pages/1-introduction

• Authors: Barbara Illowsky, Susan Dean
• Publisher/website: OpenStax
• Book title: Statistics
• Publication date: Mar 27, 2020
• Location: Houston, Texas
• Book URL: https://openstax.org/books/statistics/pages/1-introduction
• Section URL: https://openstax.org/books/statistics/pages/13-1-one-way-anova

© Jan 23, 2024 Texas Education Agency (TEA). The OpenStax name, OpenStax logo, OpenStax book covers, OpenStax CNX name, and OpenStax CNX logo are not subject to the Creative Commons license and may not be reproduced without the prior and express written consent of Rice University.

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons
• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

13.2: One-Way ANOVA

• Last updated
• Save as PDF
• Page ID 807

The purpose of a one-way ANOVA test is to determine the existence of a statistically significant difference among several group means. The test actually uses variances to help determine if the means are equal or not. To perform a one-way ANOVA test, there are several basic assumptions to be fulfilled:

Five basic assumptions of one-way ANOVA to be fulfilled

• Each population from which a sample is taken is assumed to be normal.
• All samples are randomly selected and independent.
• The populations are assumed to have equal standard deviations (or variances).
• The factor is a categorical variable.
• The response is a numerical variable.

The Null and Alternative Hypotheses

The null hypothesis is simply that all the group population means are the same. The alternative hypothesis is that at least one pair of means is different. For example, if there are \(k\) groups:

• \(H_{0}: \mu_{1} = \mu_{2} = \mu_{3} = \dotsc = \mu_{k}\)
• \(H_{a}: \text{At least two of the group means} \mu_{2} = \mu_{3} = \dotsc = \mu_{k} \text{are not equal}\)

The graphs, a set of box plots representing the distribution of values with the group means indicated by a horizontal line through the box, help in the understanding of the hypothesis test. In the first graph (red box plots), \(H_{0}: \mu_{1} = \mu_{2} = \mu_{3}\) and the three populations have the same distribution if the null hypothesis is true. The variance of the combined data is approximately the same as the variance of each of the populations.

If the null hypothesis is false, then the variance of the combined data is larger which is caused by the different means as shown in the second graph (green box plots).

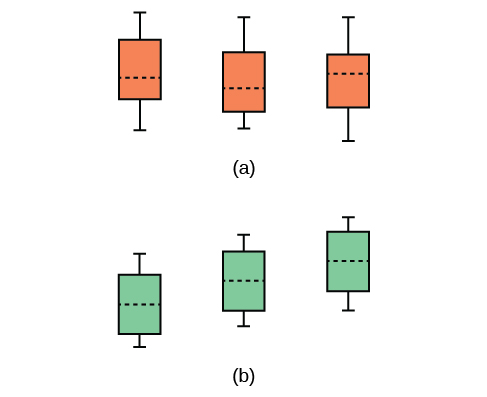
Analysis of variance extends the comparison of two groups to several, each a level of a categorical variable (factor). Samples from each group are independent, and must be randomly selected from normal populations with equal variances. We test the null hypothesis of equal means of the response in every group versus the alternative hypothesis of one or more group means being different from the others. A one-way ANOVA hypothesis test determines if several population means are equal. The distribution for the test is the \(F\) distribution with two different degrees of freedom.

Assumptions:

• all populations of interest are normally distributed.
• the populations have equal standard deviations.
• samples (not necessarily of the same size) are randomly and independently selected from each population.

The test statistic for analysis of variance is the \(F\)-ratio.

Contributors and Attributions

Barbara Illowsky and Susan Dean (De Anza College) with many other contributing authors. Content produced by OpenStax College is licensed under a Creative Commons Attribution License 4.0 license. Download for free at http://cnx.org/contents/[email protected] .