hypothesis and conclusion

Statistics Made Easy

How to Write Hypothesis Test Conclusions (With Examples)

A hypothesis test is used to test whether or not some hypothesis about a population parameter is true.

To perform a hypothesis test in the real world, researchers obtain a random sample from the population and perform a hypothesis test on the sample data, using a null and alternative hypothesis:

Null Hypothesis (H 0 ): The sample data occurs purely from chance.
Alternative Hypothesis (H A ): The sample data is influenced by some non-random cause.

If the p-value of the hypothesis test is less than some significance level (e.g. α = .05), then we reject the null hypothesis .

Otherwise, if the p-value is not less than some significance level then we fail to reject the null hypothesis .

When writing the conclusion of a hypothesis test, we typically include:

Whether we reject or fail to reject the null hypothesis.
The significance level.
A short explanation in the context of the hypothesis test.

For example, we would write:

We reject the null hypothesis at the 5% significance level. There is sufficient evidence to support the claim that…

Or, we would write:

We fail to reject the null hypothesis at the 5% significance level. There is not sufficient evidence to support the claim that…

The following examples show how to write a hypothesis test conclusion in both scenarios.

Example 1: Reject the Null Hypothesis Conclusion

Suppose a biologist believes that a certain fertilizer will cause plants to grow more during a one-month period than they normally do, which is currently 20 inches. To test this, she applies the fertilizer to each of the plants in her laboratory for one month.

She then performs a hypothesis test at a 5% significance level using the following hypotheses:

H 0 : μ = 20 inches (the fertilizer will have no effect on the mean plant growth)
H A : μ > 20 inches (the fertilizer will cause mean plant growth to increase)

Suppose the p-value of the test turns out to be 0.002.

Here is how she would report the results of the hypothesis test:

We reject the null hypothesis at the 5% significance level. There is sufficient evidence to support the claim that this particular fertilizer causes plants to grow more during a one-month period than they normally do.

Example 2: Fail to Reject the Null Hypothesis Conclusion

Suppose the manager of a manufacturing plant wants to test whether or not some new method changes the number of defective widgets produced per month, which is currently 250. To test this, he measures the mean number of defective widgets produced before and after using the new method for one month.

He performs a hypothesis test at a 10% significance level using the following hypotheses:

H 0 : μ after = μ before (the mean number of defective widgets is the same before and after using the new method)
H A : μ after ≠ μ before (the mean number of defective widgets produced is different before and after using the new method)

Suppose the p-value of the test turns out to be 0.27.

Here is how he would report the results of the hypothesis test:

We fail to reject the null hypothesis at the 10% significance level. There is not sufficient evidence to support the claim that the new method leads to a change in the number of defective widgets produced per month.

Additional Resources

The following tutorials provide additional information about hypothesis testing:

Introduction to Hypothesis Testing 4 Examples of Hypothesis Testing in Real Life How to Write a Null Hypothesis

Hey there. My name is Zach Bobbitt. I have a Master of Science degree in Applied Statistics and I’ve worked on machine learning algorithms for professional businesses in both healthcare and retail. I’m passionate about statistics, machine learning, and data visualization and I created Statology to be a resource for both students and teachers alike. My goal with this site is to help you learn statistics through using simple terms, plenty of real-world examples, and helpful illustrations.

How to Write a Great Hypothesis

Hypothesis Definition, Format, Examples, and Tips

Kendra Cherry, MS, is a psychosocial rehabilitation specialist, psychology educator, and author of the "Everything Psychology Book."

Amy Morin, LCSW, is a psychotherapist and international bestselling author. Her books, including "13 Things Mentally Strong People Don't Do," have been translated into more than 40 languages. Her TEDx talk, "The Secret of Becoming Mentally Strong," is one of the most viewed talks of all time.

Verywell / Alex Dos Diaz

The Scientific Method

Hypothesis Format

Falsifiability of a hypothesis.

Operationalization

Hypothesis Types

Hypotheses examples.

Collecting Data

A hypothesis is a tentative statement about the relationship between two or more variables. It is a specific, testable prediction about what you expect to happen in a study. It is a preliminary answer to your question that helps guide the research process.

Consider a study designed to examine the relationship between sleep deprivation and test performance. The hypothesis might be: "This study is designed to assess the hypothesis that sleep-deprived people will perform worse on a test than individuals who are not sleep-deprived."

At a Glance

A hypothesis is crucial to scientific research because it offers a clear direction for what the researchers are looking to find. This allows them to design experiments to test their predictions and add to our scientific knowledge about the world. This article explores how a hypothesis is used in psychology research, how to write a good hypothesis, and the different types of hypotheses you might use.

The Hypothesis in the Scientific Method

In the scientific method , whether it involves research in psychology, biology, or some other area, a hypothesis represents what the researchers think will happen in an experiment. The scientific method involves the following steps:

Forming a question
Performing background research
Creating a hypothesis
Designing an experiment
Collecting data
Analyzing the results
Drawing conclusions
Communicating the results

The hypothesis is a prediction, but it involves more than a guess. Most of the time, the hypothesis begins with a question which is then explored through background research. At this point, researchers then begin to develop a testable hypothesis.

Unless you are creating an exploratory study, your hypothesis should always explain what you expect to happen.

In a study exploring the effects of a particular drug, the hypothesis might be that researchers expect the drug to have some type of effect on the symptoms of a specific illness. In psychology, the hypothesis might focus on how a certain aspect of the environment might influence a particular behavior.

Remember, a hypothesis does not have to be correct. While the hypothesis predicts what the researchers expect to see, the goal of the research is to determine whether this guess is right or wrong. When conducting an experiment, researchers might explore numerous factors to determine which ones might contribute to the ultimate outcome.

In many cases, researchers may find that the results of an experiment do not support the original hypothesis. When writing up these results, the researchers might suggest other options that should be explored in future studies.

In many cases, researchers might draw a hypothesis from a specific theory or build on previous research. For example, prior research has shown that stress can impact the immune system. So a researcher might hypothesize: "People with high-stress levels will be more likely to contract a common cold after being exposed to the virus than people who have low-stress levels."

In other instances, researchers might look at commonly held beliefs or folk wisdom. "Birds of a feather flock together" is one example of folk adage that a psychologist might try to investigate. The researcher might pose a specific hypothesis that "People tend to select romantic partners who are similar to them in interests and educational level."

Elements of a Good Hypothesis

So how do you write a good hypothesis? When trying to come up with a hypothesis for your research or experiments, ask yourself the following questions:

Is your hypothesis based on your research on a topic?
Can your hypothesis be tested?
Does your hypothesis include independent and dependent variables?

Before you come up with a specific hypothesis, spend some time doing background research. Once you have completed a literature review, start thinking about potential questions you still have. Pay attention to the discussion section in the journal articles you read . Many authors will suggest questions that still need to be explored.

How to Formulate a Good Hypothesis

To form a hypothesis, you should take these steps:

Collect as many observations about a topic or problem as you can.
Evaluate these observations and look for possible causes of the problem.
Create a list of possible explanations that you might want to explore.
After you have developed some possible hypotheses, think of ways that you could confirm or disprove each hypothesis through experimentation. This is known as falsifiability.

In the scientific method , falsifiability is an important part of any valid hypothesis. In order to test a claim scientifically, it must be possible that the claim could be proven false.

Students sometimes confuse the idea of falsifiability with the idea that it means that something is false, which is not the case. What falsifiability means is that if something was false, then it is possible to demonstrate that it is false.

One of the hallmarks of pseudoscience is that it makes claims that cannot be refuted or proven false.

The Importance of Operational Definitions

A variable is a factor or element that can be changed and manipulated in ways that are observable and measurable. However, the researcher must also define how the variable will be manipulated and measured in the study.

Operational definitions are specific definitions for all relevant factors in a study. This process helps make vague or ambiguous concepts detailed and measurable.

For example, a researcher might operationally define the variable " test anxiety " as the results of a self-report measure of anxiety experienced during an exam. A "study habits" variable might be defined by the amount of studying that actually occurs as measured by time.

These precise descriptions are important because many things can be measured in various ways. Clearly defining these variables and how they are measured helps ensure that other researchers can replicate your results.

Replicability

One of the basic principles of any type of scientific research is that the results must be replicable.

Replication means repeating an experiment in the same way to produce the same results. By clearly detailing the specifics of how the variables were measured and manipulated, other researchers can better understand the results and repeat the study if needed.

Some variables are more difficult than others to define. For example, how would you operationally define a variable such as aggression ? For obvious ethical reasons, researchers cannot create a situation in which a person behaves aggressively toward others.

To measure this variable, the researcher must devise a measurement that assesses aggressive behavior without harming others. The researcher might utilize a simulated task to measure aggressiveness in this situation.

Hypothesis Checklist

Does your hypothesis focus on something that you can actually test?
Does your hypothesis include both an independent and dependent variable?
Can you manipulate the variables?
Can your hypothesis be tested without violating ethical standards?

The hypothesis you use will depend on what you are investigating and hoping to find. Some of the main types of hypotheses that you might use include:

Simple hypothesis : This type of hypothesis suggests there is a relationship between one independent variable and one dependent variable.
Complex hypothesis : This type suggests a relationship between three or more variables, such as two independent and dependent variables.
Null hypothesis : This hypothesis suggests no relationship exists between two or more variables.
Alternative hypothesis : This hypothesis states the opposite of the null hypothesis.
Statistical hypothesis : This hypothesis uses statistical analysis to evaluate a representative population sample and then generalizes the findings to the larger group.
Logical hypothesis : This hypothesis assumes a relationship between variables without collecting data or evidence.

A hypothesis often follows a basic format of "If {this happens} then {this will happen}." One way to structure your hypothesis is to describe what will happen to the dependent variable if you change the independent variable .

The basic format might be: "If {these changes are made to a certain independent variable}, then we will observe {a change in a specific dependent variable}."

A few examples of simple hypotheses:

"Students who eat breakfast will perform better on a math exam than students who do not eat breakfast."
"Students who experience test anxiety before an English exam will get lower scores than students who do not experience test anxiety."
"Motorists who talk on the phone while driving will be more likely to make errors on a driving course than those who do not talk on the phone."
"Children who receive a new reading intervention will have higher reading scores than students who do not receive the intervention."

Examples of a complex hypothesis include:

"People with high-sugar diets and sedentary activity levels are more likely to develop depression."
"Younger people who are regularly exposed to green, outdoor areas have better subjective well-being than older adults who have limited exposure to green spaces."

Examples of a null hypothesis include:

"There is no difference in anxiety levels between people who take St. John's wort supplements and those who do not."
"There is no difference in scores on a memory recall task between children and adults."
"There is no difference in aggression levels between children who play first-person shooter games and those who do not."

Examples of an alternative hypothesis:

"People who take St. John's wort supplements will have less anxiety than those who do not."
"Adults will perform better on a memory task than children."
"Children who play first-person shooter games will show higher levels of aggression than children who do not."

Collecting Data on Your Hypothesis

Once a researcher has formed a testable hypothesis, the next step is to select a research design and start collecting data. The research method depends largely on exactly what they are studying. There are two basic types of research methods: descriptive research and experimental research.

Descriptive Research Methods

Descriptive research such as case studies , naturalistic observations , and surveys are often used when conducting an experiment is difficult or impossible. These methods are best used to describe different aspects of a behavior or psychological phenomenon.

Once a researcher has collected data using descriptive methods, a correlational study can examine how the variables are related. This research method might be used to investigate a hypothesis that is difficult to test experimentally.

Experimental Research Methods

Experimental methods are used to demonstrate causal relationships between variables. In an experiment, the researcher systematically manipulates a variable of interest (known as the independent variable) and measures the effect on another variable (known as the dependent variable).

Unlike correlational studies, which can only be used to determine if there is a relationship between two variables, experimental methods can be used to determine the actual nature of the relationship—whether changes in one variable actually cause another to change.

The hypothesis is a critical part of any scientific exploration. It represents what researchers expect to find in a study or experiment. In situations where the hypothesis is unsupported by the research, the research still has value. Such research helps us better understand how different aspects of the natural world relate to one another. It also helps us develop new hypotheses that can then be tested in the future.

Thompson WH, Skau S. On the scope of scientific hypotheses . R Soc Open Sci . 2023;10(8):230607. doi:10.1098/rsos.230607

Taran S, Adhikari NKJ, Fan E. Falsifiability in medicine: what clinicians can learn from Karl Popper [published correction appears in Intensive Care Med. 2021 Jun 17;:]. Intensive Care Med . 2021;47(9):1054-1056. doi:10.1007/s00134-021-06432-z

Eyler AA. Research Methods for Public Health . 1st ed. Springer Publishing Company; 2020. doi:10.1891/9780826182067.0004

Nosek BA, Errington TM. What is replication ? PLoS Biol . 2020;18(3):e3000691. doi:10.1371/journal.pbio.3000691

Aggarwal R, Ranganathan P. Study designs: Part 2 - Descriptive studies . Perspect Clin Res . 2019;10(1):34-36. doi:10.4103/picr.PICR_154_18

Nevid J. Psychology: Concepts and Applications. Wadworth, 2013.

By Kendra Cherry, MSEd Kendra Cherry, MS, is a psychosocial rehabilitation specialist, psychology educator, and author of the "Everything Psychology Book."

school Campus Bookshelves
menu_book Bookshelves
perm_media Learning Objects
login Login
how_to_reg Request Instructor Account
hub Instructor Commons
Download Page (PDF)
Download Full Book (PDF)
Periodic Table
Physics Constants
Scientific Calculator
Reference & Cite
Tools expand_more
Readability

selected template will load here

This action is not available.

1.1: Statements and Conditional Statements

Last updated
Save as PDF
Page ID 7034

Ted Sundstrom
Grand Valley State University via ScholarWorks @Grand Valley State University

Much of our work in mathematics deals with statements. In mathematics, a statement is a declarative sentence that is either true or false but not both. A statement is sometimes called a proposition . The key is that there must be no ambiguity. To be a statement, a sentence must be true or false, and it cannot be both. So a sentence such as "The sky is beautiful" is not a statement since whether the sentence is true or not is a matter of opinion. A question such as "Is it raining?" is not a statement because it is a question and is not declaring or asserting that something is true.

Some sentences that are mathematical in nature often are not statements because we may not know precisely what a variable represents. For example, the equation 2$x$+5 = 10 is not a statement since we do not know what $x$ represents. If we substitute a specific value for $x$ (such as $x$ = 3), then the resulting equation, 2$\cdot$3 +5 = 10 is a statement (which is a false statement). Following are some more examples:

There exists a real number $x$ such that 2$x$+5 = 10. This is a statement because either such a real number exists or such a real number does not exist. In this case, this is a true statement since such a real number does exist, namely $x$ = 2.5.
For each real number $x$, $2x +5 = 2 \left( x + \dfrac{5}{2}\right)$. This is a statement since either the sentence $2x +5 = 2 \left( x + \dfrac{5}{2}\right)$ is true when any real number is substituted for $x$ (in which case, the statement is true) or there is at least one real number that can be substituted for $x$ and produce a false statement (in which case, the statement is false). In this case, the given statement is true.
Solve the equation $x^2 - 7x +10 =0$. This is not a statement since it is a directive. It does not assert that something is true.
$(a+b)^2 = a^2+b^2$ is not a statement since it is not known what $a$ and $b$ represent. However, the sentence, “There exist real numbers $a$ and $b$ such that $(a+b)^2 = a^2+b^2$" is a statement. In fact, this is a true statement since there are such integers. For example, if $a=1$ and $b=0$, then $(a+b)^2 = a^2+b^2$.
Compare the statement in the previous item to the statement, “For all real numbers $a$ and $b$, $(a+b)^2 = a^2+b^2$." This is a false statement since there are values for $a$ and $b$ for which $(a+b)^2 \ne a^2+b^2$. For example, if $a=2$ and $b=3$, then $(a+b)^2 = 5^2 = 25$ and $a^2 + b^2 = 2^2 +3^2 = 13$.

Progress Check 1.1: Statements

Which of the following sentences are statements? Do not worry about determining whether a statement is true or false; just determine whether each sentence is a statement or not.

2$\cdot$7 + 8 = 22.
$(x-1) = \sqrt(x + 11)$.
$2x + 5y = 7$.
There are integers $x$ and $y$ such that $2x + 5y = 7$.
There are integers $x$ and $y$ such that $23x + 27y = 52$.
Given a line $L$ and a point $P$ not on that line, there is a unique line through $P$ that does not intersect $L$.
$(a + b)^3 = a^3 + 3a^2b + 3ab^2 + b^3$.
$(a + b)^3 = a^3 + 3a^2b + 3ab^2 + b^3$ for all real numbers $a$ and $b$.
The derivative of $f(x) = \sin x$ is $f' (x) = \cos x$.
Does the equation $3x^2 - 5x - 7 = 0$ have two real number solutions?
If $ABC$ is a right triangle with right angle at vertex $B$, and if $D$ is the midpoint of the hypotenuse, then the line segment connecting vertex $B$ to $D$ is half the length of the hypotenuse.
There do not exist three integers $x$, $y$, and $z$ such that $x^3 + y^2 = z^3$.

Add texts here. Do not delete this text first.

How Do We Decide If a Statement Is True or False?

In mathematics, we often establish that a statement is true by writing a mathematical proof. To establish that a statement is false, we often find a so-called counterexample. (These ideas will be explored later in this chapter.) So mathematicians must be able to discover and construct proofs. In addition, once the discovery has been made, the mathematician must be able to communicate this discovery to others who speak the language of mathematics. We will be dealing with these ideas throughout the text.

For now, we want to focus on what happens before we start a proof. One thing that mathematicians often do is to make a conjecture beforehand as to whether the statement is true or false. This is often done through exploration. The role of exploration in mathematics is often difficult because the goal is not to find a specific answer but simply to investigate. Following are some techniques of exploration that might be helpful.

Techniques of Exploration

Guesswork and conjectures . Formulate and write down questions and conjectures. When we make a guess in mathematics, we usually call it a conjecture.

For example, if someone makes the conjecture that $\sin(2x) = 2 \sin(x)$, for all real numbers $x$, we can test this conjecture by substituting specific values for $x$. One way to do this is to choose values of $x$ for which $\sin(x)$is known. Using $x = \frac{\pi}{4}$, we see that

$\sin(2(\frac{\pi}{4})) = \sin(\frac{\pi}{2}) = 1,$ and

$2\sin(\frac{\pi}{4}) = 2(\frac{\sqrt2}{2}) = \sqrt2$.

Since $1 \ne \sqrt2$, these calculations show that this conjecture is false. However, if we do not find a counterexample for a conjecture, we usually cannot claim the conjecture is true. The best we can say is that our examples indicate the conjecture is true. As an example, consider the conjecture that

If $x$ and $y$ are odd integers, then $x + y$ is an even integer.

We can do lots of calculation, such as $3 + 7 = 10$ and $5 + 11 = 16$, and find that every time we add two odd integers, the sum is an even integer. However, it is not possible to test every pair of odd integers, and so we can only say that the conjecture appears to be true. (We will prove that this statement is true in the next section.)

Use of prior knowledge. This also is very important. We cannot start from square one every time we explore a statement. We must make use of our acquired mathematical knowledge. For the conjecture that $\sin (2x) = 2 \sin(x)$, for all real numbers $x$, we might recall that there are trigonometric identities called “double angle identities.” We may even remember the correct identity for $\sin (2x)$, but if we do not, we can always look it up. We should recall (or find) that for all real numbers $x$, \[\sin(2x) = 2 \sin(x)\cos(x).\]
We could use this identity to argue that the conjecture “for all real numbers $x$, $\sin (2x) = 2 \sin(x)$” is false, but if we do, it is still a good idea to give a specific counterexample as we did before.
Cooperation and brainstorming . Working together is often more fruitful than working alone. When we work with someone else, we can compare notes and articulate our ideas. Thinking out loud is often a useful brainstorming method that helps generate new ideas.

Progress Check 1.2: Explorations

Use the techniques of exploration to investigate each of the following statements. Can you make a conjecture as to whether the statement is true or false? Can you determine whether it is true or false?

$(a + b)^2 = a^2 + b^2$, for all real numbers a and b.
There are integers $x$ and $y$ such that $2x + 5y = 41$.
If $x$ is an even integer, then $x^2$ is an even integer.
If $x$ and $y$ are odd integers, then $x \cdot y$ is an odd integer.

Conditional Statements

One of the most frequently used types of statements in mathematics is the so-called conditional statement. Given statements $P$ and $Q$, a statement of the form “If $P$ then $Q$” is called a conditional statement . It seems reasonable that the truth value (true or false) of the conditional statement “If $P$ then $Q$” depends on the truth values of $P$ and $Q$. The statement “If $P$ then $Q$” means that $Q$ must be true whenever $P$ is true. The statement $P$ is called the hypothesis of the conditional statement, and the statement $Q$ is called the conclusion of the conditional statement. Since conditional statements are probably the most important type of statement in mathematics, we give a more formal definition.

A conditional statement is a statement that can be written in the form “If $P$ then $Q$,” where $P$ and $Q$ are sentences. For this conditional statement, $P$ is called the hypothesis and $Q$ is called the conclusion .

Intuitively, “If $P$ then $Q$” means that $Q$ must be true whenever $P$ is true. Because conditional statements are used so often, a symbolic shorthand notation is used to represent the conditional statement “If $P$ then $Q$.” We will use the notation $P \to Q$ to represent “If $P$ then $Q$.” When $P$ and $Q$ are statements, it seems reasonable that the truth value (true or false) of the conditional statement $P \to Q$ depends on the truth values of $P$ and $Q$. There are four cases to consider:

$P$ is true and $Q$ is true.
$P$ is false and $Q$ is true.
$P$ is true and $Q$ is false.
$P$ is false and $Q$ is false.

The conditional statement $P \to Q$ means that $Q$ is true whenever $P$ is true. It says nothing about the truth value of $Q$ when $P$ is false. Using this as a guide, we define the conditional statement $P \to Q$ to be false only when $P$ is true and $Q$ is false, that is, only when the hypothesis is true and the conclusion is false. In all other cases, $P \to Q$ is true. This is summarized in Table 1.1 , which is called a truth table for the conditional statement $P \to Q$. (In Table 1.1 , T stands for “true” and F stands for “false.”)

Table 1.1: Truth Table for $P \to Q$

The important thing to remember is that the conditional statement $P \to Q$ has its own truth value. It is either true or false (and not both). Its truth value depends on the truth values for $P$ and $Q$, but some find it a bit puzzling that the conditional statement is considered to be true when the hypothesis P is false. We will provide a justification for this through the use of an example.

Example 1.3:

Suppose that I say

“If it is not raining, then Daisy is riding her bike.”

We can represent this conditional statement as $P \to Q$ where $P$ is the statement, “It is not raining” and $Q$ is the statement, “Daisy is riding her bike.”

Although it is not a perfect analogy, think of the statement $P \to Q$ as being false to mean that I lied and think of the statement $P \to Q$ as being true to mean that I did not lie. We will now check the truth value of $P \to Q$ based on the truth values of $P$ and $Q$.

Suppose that both $P$ and $Q$ are true. That is, it is not raining and Daisy is riding her bike. In this case, it seems reasonable to say that I told the truth and that$P \to Q$ is true.
Suppose that $P$ is true and $Q$ is false or that it is not raining and Daisy is not riding her bike. It would appear that by making the statement, “If it is not raining, then Daisy is riding her bike,” that I have not told the truth. So in this case, the statement $P \to Q$ is false.
Now suppose that $P$ is false and $Q$ is true or that it is raining and Daisy is riding her bike. Did I make a false statement by stating that if it is not raining, then Daisy is riding her bike? The key is that I did not make any statement about what would happen if it was raining, and so I did not tell a lie. So we consider the conditional statement, “If it is not raining, then Daisy is riding her bike,” to be true in the case where it is raining and Daisy is riding her bike.
Finally, suppose that both $P$ and $Q$ are false. That is, it is raining and Daisy is not riding her bike. As in the previous situation, since my statement was $P \to Q$, I made no claim about what would happen if it was raining, and so I did not tell a lie. So the statement $P \to Q$ cannot be false in this case and so we consider it to be true.

Progress Check 1.4: xplorations with Conditional Statements

1 . Consider the following sentence:

If $x$ is a positive real number, then $x^2 + 8x$ is a positive real number.

Although the hypothesis and conclusion of this conditional sentence are not statements, the conditional sentence itself can be considered to be a statement as long as we know what possible numbers may be used for the variable $x$. From the context of this sentence, it seems that we can substitute any positive real number for $x$. We can also substitute 0 for $x$ or a negative real number for x provided that we are willing to work with a false hypothesis in the conditional statement. (In Chapter 2 , we will learn how to be more careful and precise with these types of conditional statements.)

(a) Notice that if $x = -3$, then $x^2 + 8x = -15$, which is negative. Does this mean that the given conditional statement is false?

(b) Notice that if $x = 4$, then $x^2 + 8x = 48$, which is positive. Does this mean that the given conditional statement is true?

(c) Do you think this conditional statement is true or false? Record the results for at least five different examples where the hypothesis of this conditional statement is true.

2 . “If $n$ is a positive integer, then $n^2 - n +41$ is a prime number.” (Remember that a prime number is a positive integer greater than 1 whose only positive factors are 1 and itself.) To explore whether or not this statement is true, try using (and recording your results) for $n = 1$, $n = 2$, $n = 3$, $n = 4$, $n = 5$, and $n = 10$. Then record the results for at least four other values of $n$. Does this conditional statement appear to be true?

Further Remarks about Conditional Statements

Suppose that Ed has exactly $52 in his wallet. The following four statements will use the four possible truth combinations for the hypothesis and conclusion of a conditional statement.

If Ed has exactly $52 in his wallet, then he has $20 in his wallet. This is a true statement. Notice that both the hypothesis and the conclusion are true.
If Ed has exactly $52 in his wallet, then he has $100 in his wallet. This statement is false. Notice that the hypothesis is true and the conclusion is false.
If Ed has $100 in his wallet, then he has at least $50 in his wallet. This statement is true regardless of how much money he has in his wallet. In this case, the hypothesis is false and the conclusion is true.

This is admittedly a contrived example but it does illustrate that the conventions for the truth value of a conditional statement make sense. The message is that in order to be complete in mathematics, we need to have conventions about when a conditional statement is true and when it is false.

If $n$ is a positive integer, then $(n^2 - n + 41)$ is a prime number.

Perhaps for all of the values you tried for $n$, $(n^2 - n + 41)$ turned out to be a prime number. However, if we try $n = 41$, we ge $n^2 - n + 41 = 41^2 - 41 + 41$ $n^2 - n + 41 = 41^2$ So in the case where $n = 41$, the hypothesis is true (41 is a positive integer) and the conclusion is false $41^2$ is not prime. Therefore, 41 is a counterexample for this conjecture and the conditional statement “If $n$ is a positive integer, then $(n^2 - n + 41)$ is a prime number” is false. There are other counterexamples (such as $n = 42$, $n = 45$, and $n = 50$), but only one counterexample is needed to prove that the statement is false.

Although one example can be used to prove that a conditional statement is false, in most cases, we cannot use examples to prove that a conditional statement is true. For example, in Progress Check 1.4 , we substituted values for $x$ for the conditional statement “If $x$ is a positive real number, then $x^2 + 8x$ is a positive real number.” For every positive real number used for $x$, we saw that $x^2 + 8x$ was positive. However, this does not prove the conditional statement to be true because it is impossible to substitute every positive real number for $x$. So, although we may believe this statement is true, to be able to conclude it is true, we need to write a mathematical proof. Methods of proof will be discussed in Section 1.2 and Chapter 3 .

Progress Check 1.5: Working with a Conditional Statement

The following statement is a true statement, which is proven in many calculus texts.

If the function $f$ is differentiable at $a$, then the function $f$ is continuous at $a$.

Using only this true statement, is it possible to make a conclusion about the function in each of the following cases?

It is known that the function $f$, where $f(x) = \sin x$, is differentiable at 0.
It is known that the function $f$, where $f(x) = \sqrt[3]x$, is not differentiable at 0.
It is known that the function $f$, where $f(x) = |x|$, is continuous at 0.
It is known that the function $f$, where $f(x) = \dfrac{|x|}{x}$ is not continuous at 0.

Closure Properties of Number Systems

The primary number system used in algebra and calculus is the real number system . We usually use the symbol R to stand for the set of all real numbers. The real numbers consist of the rational numbers and the irrational numbers. The rational numbers are those real numbers that can be written as a quotient of two integers (with a nonzero denominator), and the irrational numbers are those real numbers that cannot be written as a quotient of two integers. That is, a rational number can be written in the form of a fraction, and an irrational number cannot be written in the form of a fraction. Some common irrational numbers are $\sqrt2$, $\pi$ and $e$. We usually use the symbol $\mathbb{Q}$ to represent the set of all rational numbers. (The letter $\mathbb{Q}$ is used because rational numbers are quotients of integers.) There is no standard symbol for the set of all irrational numbers.

Perhaps the most basic number system used in mathematics is the set of natural numbers . The natural numbers consist of the positive whole numbers such as 1, 2, 3, 107, and 203. We will use the symbol $\mathbb{N}$ to stand for the set of natural numbers. Another basic number system that we will be working with is the set of integers . The integers consist of zero, the positive whole numbers, and the negatives of the positive whole numbers. If $n$ is an integer, we can write $n = \dfrac{n}{1}$. So each integer is a rational number and hence also a real number.

We will use the letter $\mathbb{Z}$ to stand for the set of integers. (The letter $\mathbb{Z}$ is from the German word, $Zahlen$, for numbers.) Three of the basic properties of the integers are that the set $\mathbb{Z}$ is closed under addition , the set $\mathbb{Z}$ is closed under multiplication , and the set of integers is closed under subtraction. This means that

If $x$ and $y$ are integers, then $x + y$ is an integer;
If $x$ and $y$ are integers, then $x \cdot y$ is an integer; and
If $x$ and $y$ are integers, then $x - y$ is an integer.

Notice that these so-called closure properties are defined in terms of conditional statements. This means that if we can find one instance where the hypothesis is true and the conclusion is false, then the conditional statement is false.

Example 1.6: Closure

In order for the set of natural numbers to be closed under subtraction, the following conditional statement would have to be true: If $x$ and $y$ are natural numbers, then $x - y$ is a natural number. However, since 5 and 8 are natural numbers, $5 - 8 = -3$, which is not a natural number, this conditional statement is false. Therefore, the set of natural numbers is not closed under subtraction.
We can use the rules for multiplying fractions and the closure rules for the integers to show that the rational numbers are closed under multiplication. If $\dfrac{a}{b}$ and $\dfrac{c}{d}$ are rational numbers (so $a$, $b$, $c$, and $d$ are integers and $b$ and $d$ are not zero), then $\dfrac{a}{b} \cdot \dfrac{c}{d} = \dfrac{ac}{bd}.$ Since the integers are closed under multiplication, we know that $ac$ and $bd$ are integers and since $b \ne 0$ and $d \ne 0$, $bd \ne 0$. Hence, $\dfrac{ac}{bd}$ is a rational number and this shows that the rational numbers are closed under multiplication.

Progress Check 1.7: Closure Properties

Answer each of the following questions.

Is the set of rational numbers closed under addition? Explain.
Is the set of integers closed under division? Explain.
Is the set of rational numbers closed under subtraction? Explain.
Which of the following sentences are statements? (a) $3^2 + 4^2 = 5^2.$ (b) $a^2 + b^2 = c^2.$ (c) There exists integers $a$, $b$, and $c$ such that $a^2 + b^2 = c^2.$ (d) If $x^2 = 4$, then $x = 2.$ (e) For each real number $x$, if $x^2 = 4$, then $x = 2.$ (f) For each real number $t$, $\sin^2t + \cos^2t = 1.$ (g) $\sin x < \sin (\frac{\pi}{4}).$ (h) If $n$ is a prime number, then $n^2$ has three positive factors. (i) 1 + $\tan^2 \theta = \text{sec}^2 \theta.$ (j) Every rectangle is a parallelogram. (k) Every even natural number greater than or equal to 4 is the sum of two prime numbers.
Identify the hypothesis and the conclusion for each of the following conditional statements. (a) If $n$ is a prime number, then $n^2$ has three positive factors. (b) If $a$ is an irrational number and $b$ is an irrational number, then $a \cdot b$ is an irrational number. (c) If $p$ is a prime number, then $p = 2$ or $p$ is an odd number. (d) If $p$ is a prime number and $p \ne 2$ or $p$ is an odd number. (e) $p \ne 2$ or $p$ is a even number, then $p$ is not prime.
Determine whether each of the following conditional statements is true or false. (a) If 10 < 7, then 3 = 4. (b) If 7 < 10, then 3 = 4. (c) If 10 < 7, then 3 + 5 = 8. (d) If 7 < 10, then 3 + 5 = 8.
Determine the conditions under which each of the following conditional sentences will be a true statement. (a) If a + 2 = 5, then 8 < 5. (b) If 5 < 8, then a + 2 = 5.
Let $P$ be the statement “Student X passed every assignment in Calculus I,” and let $Q$ be the statement “Student X received a grade of C or better in Calculus I.” (a) What does it mean for $P$ to be true? What does it mean for $Q$ to be true? (b) Suppose that Student X passed every assignment in Calculus I and received a grade of B-, and that the instructor made the statement $P \to Q$. Would you say that the instructor lied or told the truth? (c) Suppose that Student X passed every assignment in Calculus I and received a grade of C-, and that the instructor made the statement $P \to Q$. Would you say that the instructor lied or told the truth? (d) Now suppose that Student X did not pass two assignments in Calculus I and received a grade of D, and that the instructor made the statement $P \to Q$. Would you say that the instructor lied or told the truth? (e) How are Parts ( 5b ), ( 5c ), and ( 5d ) related to the truth table for $P \to Q$?

Theorem If f is a quadratic function of the form $f(x) = ax^2 + bx + c$ and a < 0, then the function f has a maximum value when $x = \dfrac{-b}{2a}$. Using only this theorem, what can be concluded about the functions given by the following formulas? (a) $g (x) = -8x^2 + 5x - 2$ (b) $h (x) = -\dfrac{1}{3}x^2 + 3x$ (c) $k (x) = 8x^2 - 5x - 7$ (d) $j (x) = -\dfrac{71}{99}x^2 +210$ (e) $f (x) = -4x^2 - 3x + 7$ (f) $F (x) = -x^4 + x^3 + 9$

Theorem If $f$ is a quadratic function of the form $f(x) = ax^2 + bx + c$ and ac < 0, then the function $f$ has two x-intercepts.

Using only this theorem, what can be concluded about the functions given by the following formulas? (a) $g (x) = -8x^2 + 5x - 2$ (b) $h (x) = -\dfrac{1}{3}x^2 + 3x$ (c) $k (x) = 8x^2 - 5x - 7$ (d) $j (x) = -\dfrac{71}{99}x^2 +210$ (e) $f (x) = -4x^2 - 3x + 7$ (f) $F (x) = -x^4 + x^3 + 9$

Theorem A. If $f$ is a cubic function of the form $f (x) = x^3 - x + b$ and b > 1, then the function $f$ has exactly one $x$-intercept. Following is another theorem about $x$-intercepts of functions: Theorem B . If $f$ and $g$ are functions with $g (x) = k \cdot f (x)$, where $k$ is a nonzero real number, then $f$ and $g$ have exactly the same $x$-intercepts.

Using only these two theorems and some simple algebraic manipulations, what can be concluded about the functions given by the following formulas? (a) $f (x) = x^3 -x + 7$ (b) $g (x) = x^3 + x +7$ (c) $h (x) = -x^3 + x - 5$ (d) $k (x) = 2x^3 + 2x + 3$ (e) $r (x) = x^4 - x + 11$ (f) $F (x) = 2x^3 - 2x + 7$

(a) Is the set of natural numbers closed under division? (b) Is the set of rational numbers closed under division? (c) Is the set of nonzero rational numbers closed under division? (d) Is the set of positive rational numbers closed under division? (e) Is the set of positive real numbers closed under subtraction? (f) Is the set of negative rational numbers closed under division? (g) Is the set of negative integers closed under addition? Explorations and Activities
Exploring Propositions . In Progress Check 1.2 , we used exploration to show that certain statements were false and to make conjectures that certain statements were true. We can also use exploration to formulate a conjecture that we believe to be true. For example, if we calculate successive powers of $2, (2^1, 2^2, 2^3, 2^4, 2^5, ...)$ and examine the units digits of these numbers, we could make the following conjectures (among others): $\bullet$ If $n$ is a natural number, then the units digit of $2^n$ must be 2, 4, 6, or 8. $\bullet$ The units digits of the successive powers of 2 repeat according to the pattern “2, 4, 8, 6.” (a) Is it possible to formulate a conjecture about the units digits of successive powers of $4 (4^1, 4^2, 4^3, 4^4, 4^5,...)$? If so, formulate at least one conjecture. (b) Is it possible to formulate a conjecture about the units digit of numbers of the form $7^n - 2^n$, where $n$ is a natural number? If so, formulate a conjecture in the form of a conditional statement in the form “If $n$ is a natural number, then ... .” (c) Let $f (x) = e^(2x)$. Determine the first eight derivatives of this function. What do you observe? Formulate a conjecture that appears to be true. The conjecture should be written as a conditional statement in the form, “If n is a natural number, then ... .”

Buy Me a Coffee

Home » What is a Hypothesis – Types, Examples and Writing Guide

What is a Hypothesis – Types, Examples and Writing Guide

Table of Contents

Definition:

Hypothesis is an educated guess or proposed explanation for a phenomenon, based on some initial observations or data. It is a tentative statement that can be tested and potentially proven or disproven through further investigation and experimentation.

Hypothesis is often used in scientific research to guide the design of experiments and the collection and analysis of data. It is an essential element of the scientific method, as it allows researchers to make predictions about the outcome of their experiments and to test those predictions to determine their accuracy.

Types of Hypothesis

Types of Hypothesis are as follows:

Research Hypothesis

A research hypothesis is a statement that predicts a relationship between variables. It is usually formulated as a specific statement that can be tested through research, and it is often used in scientific research to guide the design of experiments.

Null Hypothesis

The null hypothesis is a statement that assumes there is no significant difference or relationship between variables. It is often used as a starting point for testing the research hypothesis, and if the results of the study reject the null hypothesis, it suggests that there is a significant difference or relationship between variables.

Alternative Hypothesis

An alternative hypothesis is a statement that assumes there is a significant difference or relationship between variables. It is often used as an alternative to the null hypothesis and is tested against the null hypothesis to determine which statement is more accurate.

Directional Hypothesis

A directional hypothesis is a statement that predicts the direction of the relationship between variables. For example, a researcher might predict that increasing the amount of exercise will result in a decrease in body weight.

Non-directional Hypothesis

A non-directional hypothesis is a statement that predicts the relationship between variables but does not specify the direction. For example, a researcher might predict that there is a relationship between the amount of exercise and body weight, but they do not specify whether increasing or decreasing exercise will affect body weight.

Statistical Hypothesis

A statistical hypothesis is a statement that assumes a particular statistical model or distribution for the data. It is often used in statistical analysis to test the significance of a particular result.

Composite Hypothesis

A composite hypothesis is a statement that assumes more than one condition or outcome. It can be divided into several sub-hypotheses, each of which represents a different possible outcome.

Empirical Hypothesis

An empirical hypothesis is a statement that is based on observed phenomena or data. It is often used in scientific research to develop theories or models that explain the observed phenomena.

Simple Hypothesis

A simple hypothesis is a statement that assumes only one outcome or condition. It is often used in scientific research to test a single variable or factor.

Complex Hypothesis

A complex hypothesis is a statement that assumes multiple outcomes or conditions. It is often used in scientific research to test the effects of multiple variables or factors on a particular outcome.

Applications of Hypothesis

Hypotheses are used in various fields to guide research and make predictions about the outcomes of experiments or observations. Here are some examples of how hypotheses are applied in different fields:

Science : In scientific research, hypotheses are used to test the validity of theories and models that explain natural phenomena. For example, a hypothesis might be formulated to test the effects of a particular variable on a natural system, such as the effects of climate change on an ecosystem.
Medicine : In medical research, hypotheses are used to test the effectiveness of treatments and therapies for specific conditions. For example, a hypothesis might be formulated to test the effects of a new drug on a particular disease.
Psychology : In psychology, hypotheses are used to test theories and models of human behavior and cognition. For example, a hypothesis might be formulated to test the effects of a particular stimulus on the brain or behavior.
Sociology : In sociology, hypotheses are used to test theories and models of social phenomena, such as the effects of social structures or institutions on human behavior. For example, a hypothesis might be formulated to test the effects of income inequality on crime rates.
Business : In business research, hypotheses are used to test the validity of theories and models that explain business phenomena, such as consumer behavior or market trends. For example, a hypothesis might be formulated to test the effects of a new marketing campaign on consumer buying behavior.
Engineering : In engineering, hypotheses are used to test the effectiveness of new technologies or designs. For example, a hypothesis might be formulated to test the efficiency of a new solar panel design.

How to write a Hypothesis

Here are the steps to follow when writing a hypothesis:

Identify the Research Question

The first step is to identify the research question that you want to answer through your study. This question should be clear, specific, and focused. It should be something that can be investigated empirically and that has some relevance or significance in the field.

Conduct a Literature Review

Before writing your hypothesis, it’s essential to conduct a thorough literature review to understand what is already known about the topic. This will help you to identify the research gap and formulate a hypothesis that builds on existing knowledge.

Determine the Variables

The next step is to identify the variables involved in the research question. A variable is any characteristic or factor that can vary or change. There are two types of variables: independent and dependent. The independent variable is the one that is manipulated or changed by the researcher, while the dependent variable is the one that is measured or observed as a result of the independent variable.

Formulate the Hypothesis

Based on the research question and the variables involved, you can now formulate your hypothesis. A hypothesis should be a clear and concise statement that predicts the relationship between the variables. It should be testable through empirical research and based on existing theory or evidence.

Write the Null Hypothesis

The null hypothesis is the opposite of the alternative hypothesis, which is the hypothesis that you are testing. The null hypothesis states that there is no significant difference or relationship between the variables. It is important to write the null hypothesis because it allows you to compare your results with what would be expected by chance.

Refine the Hypothesis

After formulating the hypothesis, it’s important to refine it and make it more precise. This may involve clarifying the variables, specifying the direction of the relationship, or making the hypothesis more testable.

Examples of Hypothesis

Here are a few examples of hypotheses in different fields:

Psychology : “Increased exposure to violent video games leads to increased aggressive behavior in adolescents.”
Biology : “Higher levels of carbon dioxide in the atmosphere will lead to increased plant growth.”
Sociology : “Individuals who grow up in households with higher socioeconomic status will have higher levels of education and income as adults.”
Education : “Implementing a new teaching method will result in higher student achievement scores.”
Marketing : “Customers who receive a personalized email will be more likely to make a purchase than those who receive a generic email.”
Physics : “An increase in temperature will cause an increase in the volume of a gas, assuming all other variables remain constant.”
Medicine : “Consuming a diet high in saturated fats will increase the risk of developing heart disease.”

Purpose of Hypothesis

The purpose of a hypothesis is to provide a testable explanation for an observed phenomenon or a prediction of a future outcome based on existing knowledge or theories. A hypothesis is an essential part of the scientific method and helps to guide the research process by providing a clear focus for investigation. It enables scientists to design experiments or studies to gather evidence and data that can support or refute the proposed explanation or prediction.

The formulation of a hypothesis is based on existing knowledge, observations, and theories, and it should be specific, testable, and falsifiable. A specific hypothesis helps to define the research question, which is important in the research process as it guides the selection of an appropriate research design and methodology. Testability of the hypothesis means that it can be proven or disproven through empirical data collection and analysis. Falsifiability means that the hypothesis should be formulated in such a way that it can be proven wrong if it is incorrect.

In addition to guiding the research process, the testing of hypotheses can lead to new discoveries and advancements in scientific knowledge. When a hypothesis is supported by the data, it can be used to develop new theories or models to explain the observed phenomenon. When a hypothesis is not supported by the data, it can help to refine existing theories or prompt the development of new hypotheses to explain the phenomenon.

When to use Hypothesis

Here are some common situations in which hypotheses are used:

In scientific research , hypotheses are used to guide the design of experiments and to help researchers make predictions about the outcomes of those experiments.
In social science research , hypotheses are used to test theories about human behavior, social relationships, and other phenomena.
I n business , hypotheses can be used to guide decisions about marketing, product development, and other areas. For example, a hypothesis might be that a new product will sell well in a particular market, and this hypothesis can be tested through market research.

Characteristics of Hypothesis

Here are some common characteristics of a hypothesis:

Testable : A hypothesis must be able to be tested through observation or experimentation. This means that it must be possible to collect data that will either support or refute the hypothesis.
Falsifiable : A hypothesis must be able to be proven false if it is not supported by the data. If a hypothesis cannot be falsified, then it is not a scientific hypothesis.
Clear and concise : A hypothesis should be stated in a clear and concise manner so that it can be easily understood and tested.
Based on existing knowledge : A hypothesis should be based on existing knowledge and research in the field. It should not be based on personal beliefs or opinions.
Specific : A hypothesis should be specific in terms of the variables being tested and the predicted outcome. This will help to ensure that the research is focused and well-designed.
Tentative: A hypothesis is a tentative statement or assumption that requires further testing and evidence to be confirmed or refuted. It is not a final conclusion or assertion.
Relevant : A hypothesis should be relevant to the research question or problem being studied. It should address a gap in knowledge or provide a new perspective on the issue.

Advantages of Hypothesis

Hypotheses have several advantages in scientific research and experimentation:

Guides research: A hypothesis provides a clear and specific direction for research. It helps to focus the research question, select appropriate methods and variables, and interpret the results.
Predictive powe r: A hypothesis makes predictions about the outcome of research, which can be tested through experimentation. This allows researchers to evaluate the validity of the hypothesis and make new discoveries.
Facilitates communication: A hypothesis provides a common language and framework for scientists to communicate with one another about their research. This helps to facilitate the exchange of ideas and promotes collaboration.
Efficient use of resources: A hypothesis helps researchers to use their time, resources, and funding efficiently by directing them towards specific research questions and methods that are most likely to yield results.
Provides a basis for further research: A hypothesis that is supported by data provides a basis for further research and exploration. It can lead to new hypotheses, theories, and discoveries.
Increases objectivity: A hypothesis can help to increase objectivity in research by providing a clear and specific framework for testing and interpreting results. This can reduce bias and increase the reliability of research findings.

Limitations of Hypothesis

Some Limitations of the Hypothesis are as follows:

Limited to observable phenomena: Hypotheses are limited to observable phenomena and cannot account for unobservable or intangible factors. This means that some research questions may not be amenable to hypothesis testing.
May be inaccurate or incomplete: Hypotheses are based on existing knowledge and research, which may be incomplete or inaccurate. This can lead to flawed hypotheses and erroneous conclusions.
May be biased: Hypotheses may be biased by the researcher’s own beliefs, values, or assumptions. This can lead to selective interpretation of data and a lack of objectivity in research.
Cannot prove causation: A hypothesis can only show a correlation between variables, but it cannot prove causation. This requires further experimentation and analysis.
Limited to specific contexts: Hypotheses are limited to specific contexts and may not be generalizable to other situations or populations. This means that results may not be applicable in other contexts or may require further testing.
May be affected by chance : Hypotheses may be affected by chance or random variation, which can obscure or distort the true relationship between variables.

About the author

Muhammad Hassan

Researcher, Academic Writer, Web developer

Data Collection – Methods Types and Examples

Delimitations in Research – Types, Examples and...

Research Process – Steps, Examples and Tips

Research Design – Types, Methods and Examples

Institutional Review Board – Application Sample...

Evaluating Research – Process, Examples and...

Understanding the Role of Hypotheses and Conclusions in Mathematical Reasoning

Hypothesis and conclusion.

In the context of mathematics and logic, a hypothesis is a statement or proposition that is assumed to be true for the purpose of a logical argument or investigation. It is usually denoted by “H” or “P” and is the starting point for many mathematical proofs.

For example, let’s consider the hypothesis: “If it is raining outside, then the ground is wet.” This statement assumes that whenever it rains, the ground will be wet.

The conclusion, on the other hand, is the statement or proposition that is inferred or reached by logical reasoning, based on the hypothesis or given information. It is typically denoted by “C” or “Q”.

Using the same example, the conclusion derived from the hypothesis could be: “It is currently raining outside, so the ground is wet.” This conclusion is based on the assumption that the given condition of rain implies a wet ground.

In mathematics, hypotheses and conclusions are commonly used in proofs and logical arguments. By stating a hypothesis and then deducing a conclusion from it, mathematicians can demonstrate the validity of certain mathematical concepts, theorems, or formulas.

It’s important to note that in mathematics, a hypothesis is not the same as a guess or a prediction. It is a statement that is assumed to be true and serves as the basis for logical reasoning, while the conclusion is the logical consequence or outcome that is drawn from the hypothesis.

Formula for cyclic adenosine monophosphate & Its Significance

Is the formula of cyclic adenosine monophosphate (cAMP) $ce{C_{10}H_{11}N_{5}O_{6}P}$ or $ce{C_{10}H_{12}N_{5}O_{6}P}$? Does it matter? The correct formula for cyclic adenosine monophosphate (cAMP) is $ce{C_{10}H_{11}N_{5}O_{6}P}$. The

Development of a Turtle Inside its Egg

How does a turtle develop inside its egg? The development of a turtle inside its egg is a fascinating process that involves several stages and

The Essential Molecule in Photosynthesis for Energy and Biomass

Why does photosynthesis specifically produce glucose? Photosynthesis is the biological process by which plants, algae, and some bacteria convert sunlight, carbon dioxide (CO2), and water

How the Human Body Recycles its Energy Currency

Source for “The human body recycles its body weight of ATP each day”? The statement that “the human body recycles its body weight of ATP

Don't Miss Out! Sign Up Now!

Resources Home 🏠
Try SciSpace Copilot
Search research papers
Add Copilot Extension
Try AI Detector
Try Paraphraser
Try Citation Generator
April Papers
June Papers
July Papers

The Craft of Writing a Strong Hypothesis

Writing a hypothesis is one of the essential elements of a scientific research paper. It needs to be to the point, clearly communicating what your research is trying to accomplish. A blurry, drawn-out, or complexly-structured hypothesis can confuse your readers. Or worse, the editor and peer reviewers.

A captivating hypothesis is not too intricate. This blog will take you through the process so that, by the end of it, you have a better idea of how to convey your research paper's intent in just one sentence.

What is a Hypothesis?

The first step in your scientific endeavor, a hypothesis, is a strong, concise statement that forms the basis of your research. It is not the same as a thesis statement , which is a brief summary of your research paper .

The sole purpose of a hypothesis is to predict your paper's findings, data, and conclusion. It comes from a place of curiosity and intuition . When you write a hypothesis, you're essentially making an educated guess based on scientific prejudices and evidence, which is further proven or disproven through the scientific method.

The reason for undertaking research is to observe a specific phenomenon. A hypothesis, therefore, lays out what the said phenomenon is. And it does so through two variables, an independent and dependent variable.

The independent variable is the cause behind the observation, while the dependent variable is the effect of the cause. A good example of this is “mixing red and blue forms purple.” In this hypothesis, mixing red and blue is the independent variable as you're combining the two colors at your own will. The formation of purple is the dependent variable as, in this case, it is conditional to the independent variable.

Different Types of Hypotheses‌

Types of hypotheses

Some would stand by the notion that there are only two types of hypotheses: a Null hypothesis and an Alternative hypothesis. While that may have some truth to it, it would be better to fully distinguish the most common forms as these terms come up so often, which might leave you out of context.

Apart from Null and Alternative, there are Complex, Simple, Directional, Non-Directional, Statistical, and Associative and casual hypotheses. They don't necessarily have to be exclusive, as one hypothesis can tick many boxes, but knowing the distinctions between them will make it easier for you to construct your own.

1. Null hypothesis

A null hypothesis proposes no relationship between two variables. Denoted by H 0 , it is a negative statement like “Attending physiotherapy sessions does not affect athletes' on-field performance.” Here, the author claims physiotherapy sessions have no effect on on-field performances. Even if there is, it's only a coincidence.

2. Alternative hypothesis

Considered to be the opposite of a null hypothesis, an alternative hypothesis is donated as H1 or Ha. It explicitly states that the dependent variable affects the independent variable. A good alternative hypothesis example is “Attending physiotherapy sessions improves athletes' on-field performance.” or “Water evaporates at 100 °C. ” The alternative hypothesis further branches into directional and non-directional.

Directional hypothesis: A hypothesis that states the result would be either positive or negative is called directional hypothesis. It accompanies H1 with either the ‘<' or ‘>' sign.
Non-directional hypothesis: A non-directional hypothesis only claims an effect on the dependent variable. It does not clarify whether the result would be positive or negative. The sign for a non-directional hypothesis is ‘≠.'

3. Simple hypothesis

A simple hypothesis is a statement made to reflect the relation between exactly two variables. One independent and one dependent. Consider the example, “Smoking is a prominent cause of lung cancer." The dependent variable, lung cancer, is dependent on the independent variable, smoking.

4. Complex hypothesis

In contrast to a simple hypothesis, a complex hypothesis implies the relationship between multiple independent and dependent variables. For instance, “Individuals who eat more fruits tend to have higher immunity, lesser cholesterol, and high metabolism.” The independent variable is eating more fruits, while the dependent variables are higher immunity, lesser cholesterol, and high metabolism.

5. Associative and casual hypothesis

Associative and casual hypotheses don't exhibit how many variables there will be. They define the relationship between the variables. In an associative hypothesis, changing any one variable, dependent or independent, affects others. In a casual hypothesis, the independent variable directly affects the dependent.

6. Empirical hypothesis

Also referred to as the working hypothesis, an empirical hypothesis claims a theory's validation via experiments and observation. This way, the statement appears justifiable and different from a wild guess.

Say, the hypothesis is “Women who take iron tablets face a lesser risk of anemia than those who take vitamin B12.” This is an example of an empirical hypothesis where the researcher the statement after assessing a group of women who take iron tablets and charting the findings.

7. Statistical hypothesis

The point of a statistical hypothesis is to test an already existing hypothesis by studying a population sample. Hypothesis like “44% of the Indian population belong in the age group of 22-27.” leverage evidence to prove or disprove a particular statement.

Characteristics of a Good Hypothesis

Writing a hypothesis is essential as it can make or break your research for you. That includes your chances of getting published in a journal. So when you're designing one, keep an eye out for these pointers:

A research hypothesis has to be simple yet clear to look justifiable enough.
It has to be testable — your research would be rendered pointless if too far-fetched into reality or limited by technology.
It has to be precise about the results —what you are trying to do and achieve through it should come out in your hypothesis.
A research hypothesis should be self-explanatory, leaving no doubt in the reader's mind.
If you are developing a relational hypothesis, you need to include the variables and establish an appropriate relationship among them.
A hypothesis must keep and reflect the scope for further investigations and experiments.

Separating a Hypothesis from a Prediction

Outside of academia, hypothesis and prediction are often used interchangeably. In research writing, this is not only confusing but also incorrect. And although a hypothesis and prediction are guesses at their core, there are many differences between them.

A hypothesis is an educated guess or even a testable prediction validated through research. It aims to analyze the gathered evidence and facts to define a relationship between variables and put forth a logical explanation behind the nature of events.

Predictions are assumptions or expected outcomes made without any backing evidence. They are more fictionally inclined regardless of where they originate from.

For this reason, a hypothesis holds much more weight than a prediction. It sticks to the scientific method rather than pure guesswork. "Planets revolve around the Sun." is an example of a hypothesis as it is previous knowledge and observed trends. Additionally, we can test it through the scientific method.

Whereas "COVID-19 will be eradicated by 2030." is a prediction. Even though it results from past trends, we can't prove or disprove it. So, the only way this gets validated is to wait and watch if COVID-19 cases end by 2030.

Finally, How to Write a Hypothesis

Quick tips on writing a hypothesis

1. Be clear about your research question

A hypothesis should instantly address the research question or the problem statement. To do so, you need to ask a question. Understand the constraints of your undertaken research topic and then formulate a simple and topic-centric problem. Only after that can you develop a hypothesis and further test for evidence.

2. Carry out a recce

Once you have your research's foundation laid out, it would be best to conduct preliminary research. Go through previous theories, academic papers, data, and experiments before you start curating your research hypothesis. It will give you an idea of your hypothesis's viability or originality.

Making use of references from relevant research papers helps draft a good research hypothesis. SciSpace Discover offers a repository of over 270 million research papers to browse through and gain a deeper understanding of related studies on a particular topic. Additionally, you can use SciSpace Copilot , your AI research assistant, for reading any lengthy research paper and getting a more summarized context of it. A hypothesis can be formed after evaluating many such summarized research papers. Copilot also offers explanations for theories and equations, explains paper in simplified version, allows you to highlight any text in the paper or clip math equations and tables and provides a deeper, clear understanding of what is being said. This can improve the hypothesis by helping you identify potential research gaps.

3. Create a 3-dimensional hypothesis

Variables are an essential part of any reasonable hypothesis. So, identify your independent and dependent variable(s) and form a correlation between them. The ideal way to do this is to write the hypothetical assumption in the ‘if-then' form. If you use this form, make sure that you state the predefined relationship between the variables.

In another way, you can choose to present your hypothesis as a comparison between two variables. Here, you must specify the difference you expect to observe in the results.

4. Write the first draft

Now that everything is in place, it's time to write your hypothesis. For starters, create the first draft. In this version, write what you expect to find from your research.

Clearly separate your independent and dependent variables and the link between them. Don't fixate on syntax at this stage. The goal is to ensure your hypothesis addresses the issue.

5. Proof your hypothesis

After preparing the first draft of your hypothesis, you need to inspect it thoroughly. It should tick all the boxes, like being concise, straightforward, relevant, and accurate. Your final hypothesis has to be well-structured as well.

Research projects are an exciting and crucial part of being a scholar. And once you have your research question, you need a great hypothesis to begin conducting research. Thus, knowing how to write a hypothesis is very important.

Now that you have a firmer grasp on what a good hypothesis constitutes, the different kinds there are, and what process to follow, you will find it much easier to write your hypothesis, which ultimately helps your research.

Now it's easier than ever to streamline your research workflow with SciSpace Discover . Its integrated, comprehensive end-to-end platform for research allows scholars to easily discover, write and publish their research and fosters collaboration.

It includes everything you need, including a repository of over 270 million research papers across disciplines, SEO-optimized summaries and public profiles to show your expertise and experience.

If you found these tips on writing a research hypothesis useful, head over to our blog on Statistical Hypothesis Testing to learn about the top researchers, papers, and institutions in this domain.

Frequently Asked Questions (FAQs)

1. what is the definition of hypothesis.

According to the Oxford dictionary, a hypothesis is defined as “An idea or explanation of something that is based on a few known facts, but that has not yet been proved to be true or correct”.

2. What is an example of hypothesis?

The hypothesis is a statement that proposes a relationship between two or more variables. An example: "If we increase the number of new users who join our platform by 25%, then we will see an increase in revenue."

3. What is an example of null hypothesis?

A null hypothesis is a statement that there is no relationship between two variables. The null hypothesis is written as H0. The null hypothesis states that there is no effect. For example, if you're studying whether or not a particular type of exercise increases strength, your null hypothesis will be "there is no difference in strength between people who exercise and people who don't."

4. What are the types of research?

• Fundamental research

• Applied research

• Qualitative research

• Quantitative research

• Mixed research

• Exploratory research

• Longitudinal research

• Cross-sectional research

• Field research

• Laboratory research

• Fixed research

• Flexible research

• Action research

• Policy research

• Classification research

• Comparative research

• Causal research

• Inductive research

• Deductive research

5. How to write a hypothesis?

• Your hypothesis should be able to predict the relationship and outcome.

• Avoid wordiness by keeping it simple and brief.

• Your hypothesis should contain observable and testable outcomes.

• Your hypothesis should be relevant to the research question.

6. What are the 2 types of hypothesis?

• Null hypotheses are used to test the claim that "there is no difference between two groups of data".

• Alternative hypotheses test the claim that "there is a difference between two data groups".

7. Difference between research question and research hypothesis?

A research question is a broad, open-ended question you will try to answer through your research. A hypothesis is a statement based on prior research or theory that you expect to be true due to your study. Example - Research question: What are the factors that influence the adoption of the new technology? Research hypothesis: There is a positive relationship between age, education and income level with the adoption of the new technology.

8. What is plural for hypothesis?

The plural of hypothesis is hypotheses. Here's an example of how it would be used in a statement, "Numerous well-considered hypotheses are presented in this part, and they are supported by tables and figures that are well-illustrated."

9. What is the red queen hypothesis?

The red queen hypothesis in evolutionary biology states that species must constantly evolve to avoid extinction because if they don't, they will be outcompeted by other species that are evolving. Leigh Van Valen first proposed it in 1973; since then, it has been tested and substantiated many times.

10. Who is known as the father of null hypothesis?

The father of the null hypothesis is Sir Ronald Fisher. He published a paper in 1925 that introduced the concept of null hypothesis testing, and he was also the first to use the term itself.

11. When to reject null hypothesis?

You need to find a significant difference between your two populations to reject the null hypothesis. You can determine that by running statistical tests such as an independent sample t-test or a dependent sample t-test. You should reject the null hypothesis if the p-value is less than 0.05.

Consensus GPT vs. SciSpace GPT: Choose the Best GPT for Research

Literature Review and Theoretical Framework: Understanding the Differences

Types of Essays in Academic Writing - Quick Guide (2024)

Understanding Logical Statements

Learning Objectives

Identify the hypothesis and conclusion in a logical statement.
Determine whether mathematical statements involving linear, quadratic, absolute value expressions, equations, or inequalities are always, sometimes, or never true.
Use counterexamples to show that a statement is false, and recognize that a single counterexample is sufficient.

Introduction

Logic is an essential part of the study of mathematics. Much of mathematics is concerned with the characteristics of numbers and other mathematical objects (such as geometric figures or variables), and being able to make decisions about what must be true based on known characteristics and other facts is vital.

The Parts of a Logical Statement

A logical statement A statement that allows drawing a conclusion or result based on a hypothesis or premise. is a statement that, when true, allows us to take a known set of facts and infer (or assume) a new fact from them. Logical statements have two parts: The hypothesis The part of a logical statement that provides the premise on which the conclusion is based. In a statement “If `x` then `y` ,” the hypothesis is `x` . , which is the premise or set of facts that we start with, and the conclusion The part of a logical statement that provides the result or consequences of the hypothesis. In a statement “If `x` then `y` ,” the conclusion is `y` . , which is the new fact that we can infer when the hypothesis is true. (Note: If you've used hypothesis in science class, you've probably noticed that this is a fairly different definition. Be careful not to get confused!)

Consider this statement:

If you go outside without any rain gear or cover when it’s pouring rain, you will get wet.

Here, the hypothesis is “you go outside without any rain gear or cover when it’s pouring rain.” The hypothesis must be completely true before we can use the statement to infer anything new from it. What does this statement say about someone who doesn’t go outside? About someone who uses an umbrella? About what happens to someone when it’s not pouring rain? Nothing. This statement doesn't apply to anyone in those cases.

The conclusion of this statement is “you will get wet.” Suppose it’s raining, and someone walks outside, and doesn't have any rain gear or other kind of cover—what will happen? All the parts of the hypothesis have been met, so—if the statement is true—we can infer that the person is going to get wet. It certainly seems reasonable that they would!

Note that in this example, if the hypothesis isn’t true, the person still could get wet. On a sunny day with no rain, someone might go outside to wash his car and get sprayed by the hose. Someone else might go swimming, and then they would really get wet! The statement says nothing when the hypothesis is false. It's only helpful when the hypothesis is true.

Not all logical statements are written as “If (something is true) then (something else is true).” To identify the hypothesis and conclusion, you may need to try to rewrite a statement in an “if-then” format.

Logical statements can also be about mathematics, of course! Anything that lets us infer a new fact about something mathematical from given information is a logical statement. For example, “The diagonals of a rectangle have the same length” is a logical statement. The hypothesis is the part that can help us if we know it’s true. When could this statement be useful?

With algebraic statements, the hypothesis is often an assumption about what values are allowed for a variable. For example, you might have seen a statement like “ `a + b = b + a` , where `a` and `b` are real numbers.” Let's treat this equation as a logical statement:

Testing for Truth

Critical thinking is important, not just in mathematics but in everyday life. Have you ever heard someone make a statement and then thought, “Wait. Is that true?” Sometimes people have reasons for thinking something is true even though it isn’t. Determining if a statement is true is a great skill to have!

When determining if a statement is true, most people start by looking for examples A situation that suggests a logical statement may be true. , which are situations for which the statement does turn out to be true (both the hypothesis and the conclusion are true). A more powerful situation to find, if one exists, is a counterexample A situation that provides evidence that a logical statement is false. , a situation for which the statement turns out to be false (the hypothesis is true, but the conclusion is false). Why are counterexamples so powerful?

Consider a person who sees the moon many times at night and then thinks: I’ve never seen the moon during the day. The person might then make the statement, “The moon only comes out at night.” As an if-then statement, this is the same as “If the moon is out, then it’s night.” We can all probably think of many times when we saw the moon out, and it was nighttime. These are examples, situations when the statement was true.

But in fact, the statement is not always true, and we only need to see the moon during the day once —only one counterexample—to know that the statement is not true. Many, many examples cannot prove the statement is true, but we only need one counterexample to prove it’s not!

For a given statement, then, we have three possibilities:

So how can we be sure if something is true (or never true for that matter), if we can’t rely on lots of examples? With algebraic statements, sometimes we can turn to a graph for help:

Another way to decide if something is always, sometimes, or never true is reasoning from other things we know are true. We can start with something we know is true and try to create the original statement. Let’s try this with the same example above:

When we try to put together logical arguments like that, the biggest problem can be knowing where to start. There's a good chance our first attempt(s) will run into a dead end, and we'll need to start over. Practice does make it easier. Sometimes it helps to work backward: start by assuming the conclusion is true, try to think of a related statement known to be true (or false), and then connect them. Let’s take one last look at the example above:

Another way to test the truth of a statement is to look for counterexamples. Graphs can help us there, too:

Although we know `|-x| = -x` is not always true if `x` is any real number, we also know that it is sometimes true. In fact, we can specify when it’s true—using the graph from the example, we can see it’s true when `x<=0` . We can use that fact to create a new statement:

If `x<=0` , then `|-x| = -x` .

Because of the narrower hypothesis, this statement is always true.

The Scientific Method by Science Made Simple

Understanding and using the scientific method.

The Scientific Method is a process used to design and perform experiments. It's important to minimize experimental errors and bias, and increase confidence in the accuracy of your results.

In the previous sections, we talked about how to pick a good topic and specific question to investigate. Now we will discuss how to carry out your investigation.

Steps of the Scientific Method

Observation/Research
Experimentation

Now that you have settled on the question you want to ask, it's time to use the Scientific Method to design an experiment to answer that question.

If your experiment isn't designed well, you may not get the correct answer. You may not even get any definitive answer at all!

The Scientific Method is a logical and rational order of steps by which scientists come to conclusions about the world around them. The Scientific Method helps to organize thoughts and procedures so that scientists can be confident in the answers they find.

OBSERVATION is first step, so that you know how you want to go about your research.

HYPOTHESIS is the answer you think you'll find.

PREDICTION is your specific belief about the scientific idea: If my hypothesis is true, then I predict we will discover this.

EXPERIMENT is the tool that you invent to answer the question, and

CONCLUSION is the answer that the experiment gives.

Don't worry, it isn't that complicated. Let's take a closer look at each one of these steps. Then you can understand the tools scientists use for their science experiments, and use them for your own.

OBSERVATION

This step could also be called "research." It is the first stage in understanding the problem.

After you decide on topic, and narrow it down to a specific question, you will need to research everything that you can find about it. You can collect information from your own experiences, books, the internet, or even smaller "unofficial" experiments.

Let's continue the example of a science fair idea about tomatoes in the garden. You like to garden, and notice that some tomatoes are bigger than others and wonder why.

Because of this personal experience and an interest in the problem, you decide to learn more about what makes plants grow.

For this stage of the Scientific Method, it's important to use as many sources as you can find. The more information you have on your science fair topic, the better the design of your experiment is going to be, and the better your science fair project is going to be overall.

Also try to get information from your teachers or librarians, or professionals who know something about your science fair project. They can help to guide you to a solid experimental setup.

The next stage of the Scientific Method is known as the "hypothesis." This word basically means "a possible solution to a problem, based on knowledge and research."

The hypothesis is a simple statement that defines what you think the outcome of your experiment will be.

All of the first stage of the Scientific Method -- the observation, or research stage -- is designed to help you express a problem in a single question ("Does the amount of sunlight in a garden affect tomato size?") and propose an answer to the question based on what you know. The experiment that you will design is done to test the hypothesis.

Using the example of the tomato experiment, here is an example of a hypothesis:

TOPIC: "Does the amount of sunlight a tomato plant receives affect the size of the tomatoes?"

HYPOTHESIS: "I believe that the more sunlight a tomato plant receives, the larger the tomatoes will grow.

This hypothesis is based on:

(1) Tomato plants need sunshine to make food through photosynthesis, and logically, more sun means more food, and;

(2) Through informal, exploratory observations of plants in a garden, those with more sunlight appear to grow bigger.

The hypothesis is your general statement of how you think the scientific phenomenon in question works.

Your prediction lets you get specific -- how will you demonstrate that your hypothesis is true? The experiment that you will design is done to test the prediction.

An important thing to remember during this stage of the scientific method is that once you develop a hypothesis and a prediction, you shouldn't change it, even if the results of your experiment show that you were wrong.

An incorrect prediction does NOT mean that you "failed." It just means that the experiment brought some new facts to light that maybe you hadn't thought about before.

Continuing our tomato plant example, a good prediction would be: Increasing the amount of sunlight tomato plants in my experiment receive will cause an increase in their size compared to identical plants that received the same care but less light.

This is the part of the scientific method that tests your hypothesis. An experiment is a tool that you design to find out if your ideas about your topic are right or wrong.

It is absolutely necessary to design a science fair experiment that will accurately test your hypothesis. The experiment is the most important part of the scientific method. It's the logical process that lets scientists learn about the world.

On the next page, we'll discuss the ways that you can go about designing a science fair experiment idea.

The final step in the scientific method is the conclusion. This is a summary of the experiment's results, and how those results match up to your hypothesis.

You have two options for your conclusions: based on your results, either:

(1) YOU CAN REJECT the hypothesis, or

(2) YOU CAN NOT REJECT the hypothesis.

This is an important point!

You can not PROVE the hypothesis with a single experiment, because there is a chance that you made an error somewhere along the way.

What you can say is that your results SUPPORT the original hypothesis.

If your original hypothesis didn't match up with the final results of your experiment, don't change the hypothesis.

Instead, try to explain what might have been wrong with your original hypothesis. What information were you missing when you made your prediction? What are the possible reasons the hypothesis and experimental results didn't match up?

Remember, a science fair experiment isn't a failure simply because does not agree with your hypothesis. No one will take points off if your prediction wasn't accurate. Many important scientific discoveries were made as a result of experiments gone wrong!

A science fair experiment is only a failure if its design is flawed. A flawed experiment is one that (1) doesn't keep its variables under control, and (2) doesn't sufficiently answer the question that you asked of it.

Search This Site:

Science Fairs

Introduction
Project Ideas
Types of Projects
Pick a Topic
Scientific Method
Design Your Experiment
Present Your Project
What Judges Want
Parent Info

Recommended *

Sample Science Projects - botany, ecology, microbiology, nutrition

* This site contains affiliate links to carefully chosen, high quality products. We may receive a commission for purchases made through these links.

The science fair projects & ideas, science articles and all other material on this website are covered by copyright laws and may not be reproduced without permission.

$Department of Mathematics$

Logic and Mathematical Statements

Worked examples, if...then... statements, mini-lecture., example. consider the statement "$x > 0 \rightarrow x+1>0$". is this statement true or false, example. consider the statement "if $x$ is a positive integer or a solution to $x+3>4$, then $x>0$ and $x> \frac{1}{2}$." is this statement true, example. consider the statement "$0>1 \rightarrow \sin x = 2$". is this statement true or false.

When you choose to publish with PLOS, your research makes an impact. Make your work accessible to all, without restrictions, and accelerate scientific discovery with options like preprints and published peer review that make your work more Open.

PLOS Biology
PLOS Climate
PLOS Complex Systems
PLOS Computational Biology
PLOS Digital Health
PLOS Genetics
PLOS Global Public Health
PLOS Medicine
PLOS Mental Health
PLOS Neglected Tropical Diseases
PLOS Pathogens
PLOS Sustainability and Transformation
PLOS Collections
How to Write Discussions and Conclusions

How to Write Discussions and Conclusions

The discussion section contains the results and outcomes of a study. An effective discussion informs readers what can be learned from your experiment and provides context for the results.

What makes an effective discussion?

When you’re ready to write your discussion, you’ve already introduced the purpose of your study and provided an in-depth description of the methodology. The discussion informs readers about the larger implications of your study based on the results. Highlighting these implications while not overstating the findings can be challenging, especially when you’re submitting to a journal that selects articles based on novelty or potential impact. Regardless of what journal you are submitting to, the discussion section always serves the same purpose: concluding what your study results actually mean.

A successful discussion section puts your findings in context. It should include:

the results of your research,
a discussion of related research, and
a comparison between your results and initial hypothesis.

Tip: Not all journals share the same naming conventions.

You can apply the advice in this article to the conclusion, results or discussion sections of your manuscript.

Our Early Career Researcher community tells us that the conclusion is often considered the most difficult aspect of a manuscript to write. To help, this guide provides questions to ask yourself, a basic structure to model your discussion off of and examples from published manuscripts.

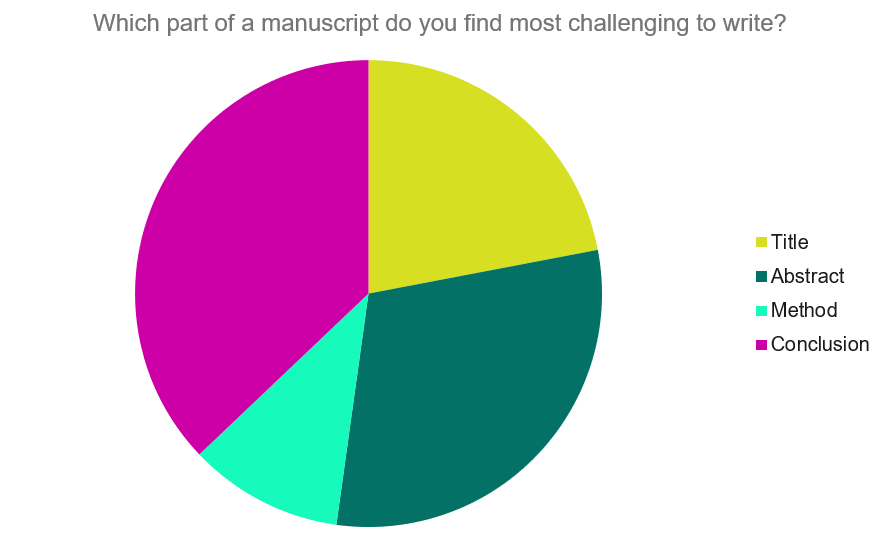
Questions to ask yourself:

Was my hypothesis correct?
If my hypothesis is partially correct or entirely different, what can be learned from the results?
How do the conclusions reshape or add onto the existing knowledge in the field? What does previous research say about the topic?
Why are the results important or relevant to your audience? Do they add further evidence to a scientific consensus or disprove prior studies?
How can future research build on these observations? What are the key experiments that must be done?
What is the “take-home” message you want your reader to leave with?

How to structure a discussion

Trying to fit a complete discussion into a single paragraph can add unnecessary stress to the writing process. If possible, you’ll want to give yourself two or three paragraphs to give the reader a comprehensive understanding of your study as a whole. Here’s one way to structure an effective discussion:

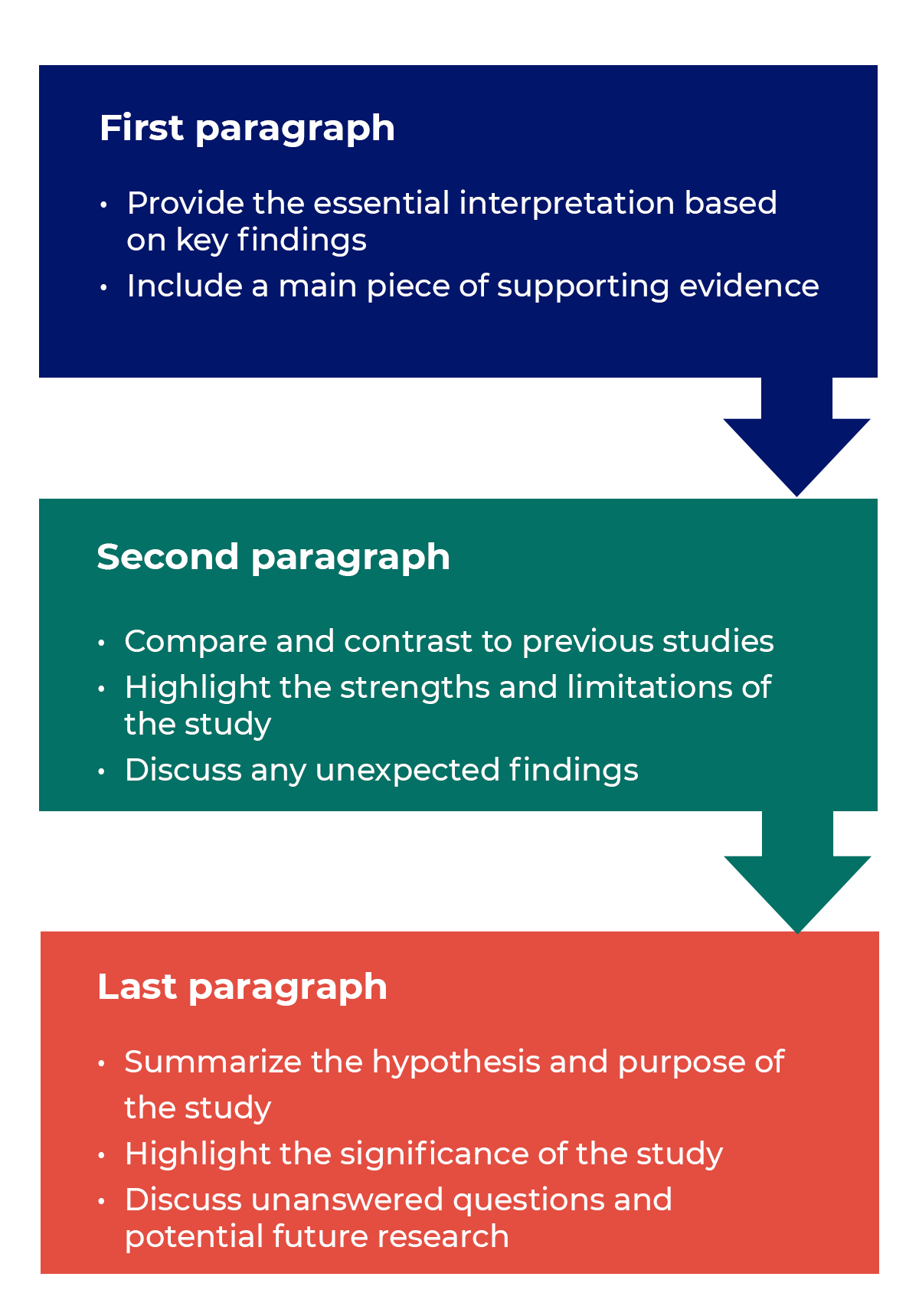
Writing Tips

While the above sections can help you brainstorm and structure your discussion, there are many common mistakes that writers revert to when having difficulties with their paper. Writing a discussion can be a delicate balance between summarizing your results, providing proper context for your research and avoiding introducing new information. Remember that your paper should be both confident and honest about the results!

Read the journal’s guidelines on the discussion and conclusion sections. If possible, learn about the guidelines before writing the discussion to ensure you’re writing to meet their expectations.
Begin with a clear statement of the principal findings. This will reinforce the main take-away for the reader and set up the rest of the discussion.
Explain why the outcomes of your study are important to the reader. Discuss the implications of your findings realistically based on previous literature, highlighting both the strengths and limitations of the research.
State whether the results prove or disprove your hypothesis. If your hypothesis was disproved, what might be the reasons?
Introduce new or expanded ways to think about the research question. Indicate what next steps can be taken to further pursue any unresolved questions.
If dealing with a contemporary or ongoing problem, such as climate change, discuss possible consequences if the problem is avoided.
Be concise. Adding unnecessary detail can distract from the main findings.

Don’t

Rewrite your abstract. Statements with “we investigated” or “we studied” generally do not belong in the discussion.
Include new arguments or evidence not previously discussed. Necessary information and evidence should be introduced in the main body of the paper.
Apologize. Even if your research contains significant limitations, don’t undermine your authority by including statements that doubt your methodology or execution.
Shy away from speaking on limitations or negative results. Including limitations and negative results will give readers a complete understanding of the presented research. Potential limitations include sources of potential bias, threats to internal or external validity, barriers to implementing an intervention and other issues inherent to the study design.
Overstate the importance of your findings. Making grand statements about how a study will fully resolve large questions can lead readers to doubt the success of the research.

Snippets of Effective Discussions:

Consumer-based actions to reduce plastic pollution in rivers: A multi-criteria decision analysis approach

Identifying reliable indicators of fitness in polar bears

How to Write a Great Title
How to Write an Abstract
How to Write Your Methods
How to Report Statistics
How to Edit Your Work

The contents of the Peer Review Center are also available as a live, interactive training session, complete with slides, talking points, and activities. …

The contents of the Writing Center are also available as a live, interactive training session, complete with slides, talking points, and activities. …

There’s a lot to consider when deciding where to submit your work. Learn how to choose a journal that will help your study reach its audience, while reflecting your values as a researcher…

Anatomy & Physiology
Astrophysics
Earth Science
Environmental Science
Organic Chemistry
Precalculus
Trigonometry
English Grammar
U.S. History
World History

... and beyond

Socratic Meta
Featured Answers

What is the difference between a hypothesis and a conclusion?

And a conclusion is drawn AFTER the experiment is performed, and reports whether or not the results of the experiment supported the original hypothesis...

Impact of this question

school Campus Bookshelves
menu_book Bookshelves
perm_media Learning Objects
login Login
how_to_reg Request Instructor Account
hub Instructor Commons
Download Page (PDF)
Download Full Book (PDF)
Periodic Table
Physics Constants
Scientific Calculator
Reference & Cite
Tools expand_more
Readability

selected template will load here

This action is not available.

2.11: If Then Statements

Last updated
Save as PDF
Page ID 2144

Hypothesis followed by a conclusion in a conditional statement.

Conditional Statements

A conditional statement (also called an if-then statement ) is a statement with a hypothesis followed by a conclusion . The hypothesis is the first, or “if,” part of a conditional statement. The conclusion is the second, or “then,” part of a conditional statement. The conclusion is the result of a hypothesis.

f-d_4db5d03aa180674c10187c8961dc571238102082156ee867771ecea3+IMAGE_TINY+IMAGE_TINY.png

If-then statements might not always be written in the “if-then” form. Here are some examples of conditional statements:

Statement 1: If you work overtime, then you’ll be paid time-and-a-half.
Statement 2: I’ll wash the car if the weather is nice.
Statement 3: If 2 divides evenly into $x$, then $x$ is an even number.
Statement 4: I’ll be a millionaire when I win the lottery.
Statement 5: All equiangular triangles are equilateral.

Statements 1 and 3 are written in the “if-then” form. The hypothesis of Statement 1 is “you work overtime.” The conclusion is “you’ll be paid time-and-a-half.” Statement 2 has the hypothesis after the conclusion. If the word “if” is in the middle of the statement, then the hypothesis is after it. The statement can be rewritten: If the weather is nice, then I will wash the car. Statement 4 uses the word “when” instead of “if” and is like Statement 2. It can be written: If I win the lottery, then I will be a millionaire. Statement 5 “if” and “then” are not there. It can be rewritten: If a triangle is equiangular, then it is equilateral.

What if you were given a statement like "All squares are rectangles"? How could you determine the hypothesis and conclusion of this statement?

Example $\PageIndex{1}$

Determine the hypothesis and conclusion: I'll bring an umbrella if it rains.

Hypothesis: "It rains." Conclusion: "I'll bring an umbrella."

Example $\PageIndex{2}$

Determine the hypothesis and conclusion: All right angles are $90^{\circ}$.

Hypothesis: "An angle is right." Conclusion: "It is $90^{\circ}$."

Example $\PageIndex{3}$

Use the statement: I will graduate when I pass Calculus.

Rewrite in if-then form and determine the hypothesis and conclusion.

This statement can be rewritten as If I pass Calculus, then I will graduate. The hypothesis is “I pass Calculus,” and the conclusion is “I will graduate.”

Example $\PageIndex{4}$

Use the statement: All prime numbers are odd.

Rewrite in if-then form, determine the hypothesis and conclusion, and determine whether this is a true statement.

This statement can be rewritten as If a number is prime, then it is odd. The hypothesis is "a number is prime" and the conclusion is "it is odd". This is not a true statement (remember that not all conditional statements will be true!) since 2 is a prime number but it is not odd.

Example $\PageIndex{5}$

Determine the hypothesis and conclusion: Sarah will go to the store if Riley does the laundry.

The statement can be rewritten as "If Riley does the laundry then Sarah will go to the store." The hypothesis is "Riley does the laundry" and the conclusion is "Sarah will go to the store."

Determine the hypothesis and the conclusion for each statement.

If 5 divides evenly into $x$, then $x$ ends in 0 or 5.
If a triangle has three congruent sides, it is an equilateral triangle.
Three points are coplanar if they all lie in the same plane.
If $x=3$, then $x^2=9$.
If you take yoga, then you are relaxed.
All baseball players wear hats.
I'll learn how to drive when I am 16 years old.
If you do your homework, then you can watch TV.
Alternate interior angles are congruent if lines are parallel.
All kids like ice cream.

Additional Resources

Video: If-Then Statements Principles - Basic

Activities: If-Then Statements Discussion Questions

Study Aids: Conditional Statements Study Guide

Practice: If Then Statements

Real World: If Then Statements

If you're seeing this message, it means we're having trouble loading external resources on our website.

If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.

To log in and use all the features of Khan Academy, please enable JavaScript in your browser.

Course: LSAT > Unit 1

Getting started with Logical Reasoning
Introduction to arguments
Catalog of question types
Types of conclusions
Types of evidence
Types of flaws
Identify the conclusion | Quick guide

Identify the conclusion | Learn more

Identify the conclusion | Examples
Identify an entailment | Quick guide
Identify an entailment | Learn more
Strongly supported inferences | Quick guide
Strongly supported inferences | Learn more
Disputes | Quick guide
Disputes | Learn more
Identify the technique | Quick guide
Identify the technique | Learn more
Identify the role | Quick guide
Identify the role | learn more
Identify the principle | Quick guide
Identify the principle | Learn more
Match structure | Quick guide
Match structure | Learn more
Match principles | Quick guide
Match principles | Learn more
Identify a flaw | Quick guide
Identify a flaw | Learn more
Match a flaw | Quick guide
Match a flaw | Learn more
Necessary assumptions | Quick guide
Necessary assumptions | Learn more
Sufficient assumptions | Quick guide
Sufficient assumptions | Learn more
Strengthen and weaken | Quick guide
Strengthen and weaken | Learn more
Helpful to know | Quick guide
Helpful to know | learn more
Explain or resolve | Quick guide
Explain or resolve | Learn more

How do we identify the main conclusion of an argument?

Some specifics.

The claim that is backed by the rest of the argument as a whole
Backed by support, but does not itself support any other claim
The claim that the argument as a whole is trying to establish
Also called intermediate or subsidiary conclusions
Claims that function as both conclusion and support
A conclusion that supports a further conclusion (or conclusions)
Backed by support, and simultaneously support a different claim

Some paleontologists have suggested that Apatosaurus, a huge dinosaur, was able to gallop. This, however, is unlikely, because galloping would probably have broken Apatosaurus’s legs. Experiments with modern bones show how much strain they can withstand before breaking. By taking into account the diameter and density of Apatosaurus leg bones, it is possible to calculate that those bones could not have withstood the strains of galloping.

(A) Galloping would probably have broken the legs of Apatosaurus.

(B) It is possible to calculate that Apatosaurus leg bones could not have withstood the strain of galloping.

(C) The claim of paleontologists that Apatosaurus was able to gallop is likely to be incorrect.

(D) If galloping would have broken the legs of Apatosaurus, then Apatosaurus was probably unable to gallop.

(E) Modern bones are quite similar in structure and physical properties to the bones of Apatosaurus.

How should we tackle this question?

Some paleontologists think the Apatosaurus could gallop, but they’re wrong.

The galloping Apatosaurus theory is wrong.

Apatosaurus couldn’t gallop.

This doesn't match our prediction, and it's also signaled in the argument by the word "because", which is a support indicator. It helps explain why the paleontologists were probably wrong.
This doesn't match our prediction, and it's part of the argument that shows why the Apatosaurus probably couldn't gallop.
This choices matches our prediction—every other claim in the argument serves to support this claim, and this claim does not , in turn, support anything else.
This might have been tempting, since it does include the main conclusion that Apatosaurus probably couldn't gallop, but it's phrased conditionally, whereas the argument isn't structured conditionally.
This doesn't match our prediction, because it's not what the arguer is trying to prove. It's somewhat implied because of the inclusion of the experiments with modern bones, but it's not what the arguer sets out to persuade us of, so it can't be the main conclusion.

Common incorrect choices

(Choice A) It is a good idea for florists to stock up on white carnations before St. Patrick's Day. A It is a good idea for florists to stock up on white carnations before St. Patrick's Day.
(Choice B) Flowers that are naturally green are very rare. B Flowers that are naturally green are very rare.
(Choice C) There are some people who like to have green carnations on St. Patrick's Day. C There are some people who like to have green carnations on St. Patrick's Day.
(Choice D) White carnations are fairly inexpensive and can easily be dyed green. D White carnations are fairly inexpensive and can easily be dyed green.
(Choice E) It is very difficult to breed green carnations. E It is very difficult to breed green carnations.
Some people like to have green carnations on St. Patrick's Day.
But flowers that are naturally green are extremely rare.
Thus, it is very difficult for plant breeders to produce green carnations.
Before St. Patrick's Day, then, it is wise for florists to stock up on white carnations,
White carnations are fairly inexpensive and quite easy to dye green.

Some final thoughts about identifying conclusions

Don't use conclusion indicator words as an automatic shortcut! It's very possible to see the word "thus" towards the end of a passage and have that claim not be the main conclusion.
If you're having trouble, use process of elimination—start with what you know to be evidence, and eliminate the choices with those claims.
To become familiar with specific types of conclusions so that you can gain speed in your argument analysis, check out our article about Types of conclusions .

Want to join the conversation?

Upvote Button navigates to signup page
Downvote Button navigates to signup page
Flag Button navigates to signup page

Mathematicians
Math Lessons
Square Roots
Math Calculators
Conclusion | Definition & Meaning

JUMP TO TOPIC

Hypothesis and Conclusion

If-then statement, a implies b, conclusion|definition & meaning.

The term conclusion in maths is used to define us about the problem that we solve and when we produce the final result at the end then that stage of processes is called as conclusion.

Figure 1 – Give the Right Conclusion to the problem

When you solve a maths question, you have to end the problem by calculating the last answer and pulling a conclus ion by writing the answer. A conclusion is the last step of the maths problem. The conclusion is the final answer produced in the end . The answer is completed by writing the arguments and statements by telling the answer to the question. The ending statement of a problem is called a conclusion.

Drawing conclusions refers to the act of thinking of interpreting a series of premises or some ideas and, from them, suggesting something that leads to a meaningful finding. It is normally regarded as a conscious way of learning .

As a rule, a mathematical statement comprises two sections : the first section is assumptions or hypotheses , and the other section is the conclusion . Most mathematical statements have the form “If A, then B.” Often, this statement is written as “A implies B” or “A $\Rightarrow $ B.” The assumptions we make are what makes “A,” and the circumstances that make “B” are called the conclusion .

To prove that a given statement “If A, then B” is said to be true, we will require some assumptions for “A,” and after doing some work on it, we need to conclude that “B” must also hold when “A” holds.

If we are asked to apply the statement “If A, then B,” firstly, we should be sure that the conditions of the statement “A” are met and true before we start to talk about the conclusion “B.”

Suppose you want to apply the statement “x is even $\Rightarrow$ x2 is an integer.” First, you must verify that x is even before you conclude that x2 is an integer.

In maths, you will, at many times, confront statements in the form “X $\Leftrightarrow$ Y” or “X if and only if Y.” These statements are actually two “if, then” statements. The following statement, “X if and only if Y,” is logically equivalent to the statements “If X, then Y” and “If Y, then X.” One more method for thinking about this kind of explanation is an equality between the statements X and Y: so, whenever X holds, Y holds, and whenever Y hold, X holds.

Assume the example: “ x is even $\Leftrightarrow$ x 2 is an integer “. Statement A says, “ x is even,” whereas statement B says, “ x 2 is an integer.” If we get a quick revision about what it suggests to be even (simply that x is a multiple of 2), we can see with ease that the following two statements are identical : If x = 2 k is proved to be even, then it implies x 2 = 2 k 2 = k is an integer, and we know that x 2 = k is an integer, then x = 2 k so n is proved to be even.

In day-to-day use, a statement which is in the form “ If A, then B ,” in some cases, means “ A if and only if B. ” For example, when people agree on a deal, they say, “If you agree to sell me your car for 500k, then I’ll buy from you this week” they straightaway mean, “I’ll buy your car if and only if you agree to sell me in 500k.” In other words, if you don’t agree on 500k, they will not be buying your car from you .

In geometry, the validation or proof is stated in the if-then format. The “if” is a condition or hypothesis , and if that condition is met, only then the second part of the statement is true , which is called the conclusion . The working is like any other if-then statement. For illustration, the statement “If a toy shop has toys for two age groups and 45 percent of toys in the shop are for 14 or above years old, then 55 percent of the toys in the shop are for 13 and fewer years old.” The above statement concludes that “55 percent of the toys in the shop are for 13 and fewer years old.”

In maths, the statement “A if and only if B” is very different from “A implies B.” Assume the example: “ x is an integer” is the A statement, and “ x 3 is a rational number” is the B statement The statement “A implies B” here means “If x is an integer, then x 3 is a rational number.” The statement is proven to be true. On the other hand, the statement, “A, if and only if B,” means “ x is an integer if and only if x 3 is a rational number,” which is not true in this case.

Examples of Drawing Conclusions

Consider the equation below. Comment if this equation is true or false.

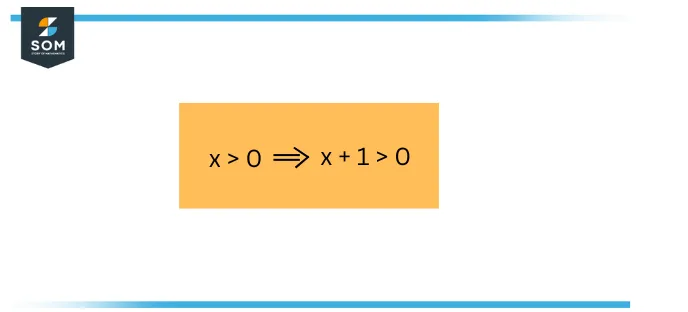
Figure 3 – Example Problem

To calculate its true answer, first, consider the hypothesis $x>0$. Whatever we are going to conclude, it will be a consequence of the truth that $x$ is positive.

Next, consider the conclusion $x+1>0$. This equation is right, since $x+1>x>0$.

This implies that the provided inequality is true.

Simplify the below problem by providing a conclusion by calculating the answer of A.

\[ A= \dfrac{35}{3} \]

The expression given in the question is: $A= \dfrac{35}{3}$

Calculating the answer of A to make a conclusion, The arithmetic operation division is found in the question that is to be figured out in the provided problem. After figuring out the answer to expression A, The conclusion will be given.

\[ A= 11. 667 \]

Therefore, we conclude the question by calculating the answer of $A=11.666$

Consider the equation $0>1 \Rightarrow sinx=2$. Is this equation true or false?

To calculate the correct answer, first consider the hypothesis $0>1$. This equation is clearly false.

calculate the below problem by providing a conclusion by estimating the value of X.

\[ 3+8 \times 2\]

The expression given in the problem is $3+8 \times 2 $.

Multiplication and Plus operation is to be carried out to calculate the answer to the given problem. After figuring out the answer to X the conclusion will be given.

Thus, we conclude the example by calculating the value of $X = 19$.

All images/mathematical drawings were created with GeoGebra.

Concentric Circles Definition < Glossary Index > Cone Definiton

IMAGES

Identifying Hypothesis and Conclusion
Best Example of How to Write a Hypothesis 2024
PPT
PPT
Hypothesis And Conclusion Research Example
How to Write a Hypothesis

VIDEO

Concept of Hypothesis
Forming the Conclusion of a Hypothesis Test
Conclusion and Hypothesis Writing
Writing the Final Conclusion for the Hypothesis Testing
විද්‍යාත්මක ක්‍රමය (Scientific method) Grade 9-O\L
Conclusion Definition & Meaning

COMMENTS

How to Write Hypothesis Test Conclusions (With Examples)
A hypothesis test is used to test whether or not some hypothesis about a population parameter is true.. To perform a hypothesis test in the real world, researchers obtain a random sample from the population and perform a hypothesis test on the sample data, using a null and alternative hypothesis:. Null Hypothesis (H 0): The sample data occurs purely from chance.
How to Write a Strong Hypothesis
A hypothesis is a statement that can be tested by scientific research. Learn how to develop, formulate, refine and phrase your hypothesis with examples and tips from Scribbr. Find out what is a null and alternative hypothesis, how to test your hypothesis and more.
Hypothesis: Definition, Examples, and Types
A hypothesis is a tentative statement about the relationship between two or more variables. It is a specific, testable prediction about what you expect to happen in a study. It is a preliminary answer to your question that helps guide the research process. Consider a study designed to examine the relationship between sleep deprivation and test ...
1.1: Statements and Conditional Statements
Using this as a guide, we define the conditional statement P → Q to be false only when P is true and Q is false, that is, only when the hypothesis is true and the conclusion is false. In all other cases, P → Q is true. This is summarized in Table 1.1, which is called a truth table for the conditional statement P → Q.
What is a Hypothesis
Tentative: A hypothesis is a tentative statement or assumption that requires further testing and evidence to be confirmed or refuted. It is not a final conclusion or assertion. Relevant: A hypothesis should be relevant to the research question or problem being studied. It should address a gap in knowledge or provide a new perspective on the issue.
The scientific method (article)
The scientific method. At the core of biology and other sciences lies a problem-solving approach called the scientific method. The scientific method has five basic steps, plus one feedback step: Make an observation. Ask a question. Form a hypothesis, or testable explanation. Make a prediction based on the hypothesis.
Understanding Logical Statements
A logical statement A statement that allows drawing a conclusion or result based on a hypothesis or premise. is a statement that, when true, allows us to take a known set of facts and infer (or assume) a new fact from them. Logical statements have two parts: The hypothesis The part of a logical statement that provides the premise on which the conclusion is based.
Understanding the Role of Hypotheses and Conclusions in Mathematical
Hypothesis and conclusion. In the context of mathematics and logic, a hypothesis is a statement or proposition that is assumed to be true for the purpose of a logical argument or investigation. It is usually denoted by "H" or "P" and is the starting point for many mathematical proofs. For example, let's consider the hypothesis: "If ...
Research Hypothesis: Definition, Types, Examples and Quick Tips
3. Simple hypothesis. A simple hypothesis is a statement made to reflect the relation between exactly two variables. One independent and one dependent. Consider the example, "Smoking is a prominent cause of lung cancer." The dependent variable, lung cancer, is dependent on the independent variable, smoking. 4.
Understanding Logical Statements
A logical statement A statement that allows drawing a conclusion or result based on a hypothesis or premise. is a statement that, when true, allows us to take a known set of facts and infer (or assume) a new fact from them. Logical statements have two parts: The hypothesis The part of a logical statement that provides the premise on which the conclusion is based.
Steps of the Scientific Method
Learn how to use the scientific method to explore observations and answer questions. Find out what a hypothesis is, how to construct one, and how to test it with an experiment. See examples of the six steps of the scientific method and how they apply to a science fair project.
Hypothesis Testing
Table of contents. Step 1: State your null and alternate hypothesis. Step 2: Collect data. Step 3: Perform a statistical test. Step 4: Decide whether to reject or fail to reject your null hypothesis. Step 5: Present your findings. Other interesting articles. Frequently asked questions about hypothesis testing.
The Scientific Method
CONCLUSION. The final step in the scientific method is the conclusion. This is a summary of the experiment's results, and how those results match up to your hypothesis. You have two options for your conclusions: based on your results, either: (1) YOU CAN REJECT the hypothesis, or (2) YOU CAN NOT REJECT the hypothesis. This is an important point!
Writing a Research Paper Conclusion
Step 1: Restate the problem. The first task of your conclusion is to remind the reader of your research problem. You will have discussed this problem in depth throughout the body, but now the point is to zoom back out from the details to the bigger picture. While you are restating a problem you've already introduced, you should avoid phrasing ...
Logic and Mathematical Statements
In general, a mathematical statement consists of two parts: the hypothesis or assumptions, and the conclusion. Most mathematical statements you will see in first year courses have the form "If A, then B" or "A implies B" or "A $\Rightarrow$ B". The conditions that make up "A" are the assumptions we make, and the conditions that make up "B" are ...
How to Write Discussions and Conclusions
Learn how to write an effective discussion section that informs readers about the results and outcomes of your study, highlights the implications of your research, and compares your results with your initial hypothesis. Find tips, questions, structure, and examples for writing a discussion that is concise, clear, and confident.
What is the difference between a hypothesis and a conclusion?
A hypothesis is something that is proposed to explain a phenomenon, and a conclusion is a statement that follows from the results of an experiment or observation. The web page explains the difference with examples and provides a link to an answer from Socratic, a platform for learning science.
2.11: If Then Statements
The conclusion is the result of a hypothesis. Figure 2.11.1 2.11. 1. If-then statements might not always be written in the "if-then" form. Here are some examples of conditional statements: Statement 1: If you work overtime, then you'll be paid time-and-a-half. Statement 2: I'll wash the car if the weather is nice.
Identify the conclusion
Sub-conclusions can be particularly hard to differentiate from the main conclusion because they're often signaled by the same keywords (thus, therefore, hence, etc.). Valid inferences: Other incorrect choices may state something that can be inferred from statements in the argument but that isn't the argument's main conclusion.
Conclusion
Hypothesis and Conclusion. As a rule, a mathematical statement comprises two sections: the first section is assumptions or hypotheses, and the other section is the conclusion.Most mathematical statements have the form "If A, then B."Often, this statement is written as "A implies B" or "A $\Rightarrow $ B." The assumptions we make are what makes "A," and the circumstances that ...
How to Write a Thesis or Dissertation Conclusion
Step 1: Answer your research question. Step 2: Summarize and reflect on your research. Step 3: Make future recommendations. Step 4: Emphasize your contributions to your field. Step 5: Wrap up your thesis or dissertation. Full conclusion example. Conclusion checklist. Other interesting articles.
IXL
SmartScore. out of 100. IXL's SmartScore is a dynamic measure of progress towards mastery, rather than a percentage grade. It tracks your skill level as you tackle progressively more difficult questions. Consistently answer questions correctly to reach excellence (90), or conquer the Challenge Zone to achieve mastery (100)!
Hypothesis vs Conclusion
As nouns the difference between hypothesis and conclusion is that hypothesis is used loosely, a tentative conjecture explaining an observation, phenomenon or scientific problem that can be tested by further observation, investigation and/or experimentation. As a scientific term of art, see the attached quotation. Compare to theory, and quotation given there while conclusion is the end, finish ...

How to Write Hypothesis Test Conclusions (With Examples)

Example 1: Reject the Null Hypothesis Conclusion

Example 2: Fail to Reject the Null Hypothesis Conclusion

Additional Resources

Leave a Reply Cancel reply

How to Write a Great Hypothesis

Hypothesis Format

Hypothesis Types

At a Glance

The Hypothesis in the Scientific Method

Elements of a Good Hypothesis

How to Formulate a Good Hypothesis

The Importance of Operational Definitions

Replicability

Hypothesis Checklist

A few examples of simple hypotheses:

Examples of a complex hypothesis include:

Examples of a null hypothesis include:

Examples of an alternative hypothesis:

Collecting Data on Your Hypothesis

Descriptive Research Methods

Experimental Research Methods

1.1: Statements and Conditional Statements

Progress Check 1.1: Statements

How Do We Decide If a Statement Is True or False?

Techniques of Exploration

Progress Check 1.2: Explorations

Conditional Statements

Example 1.3:

Progress Check 1.4: xplorations with Conditional Statements

Further Remarks about Conditional Statements

Progress Check 1.5: Working with a Conditional Statement

Closure Properties of Number Systems

Example 1.6: Closure

Progress Check 1.7: Closure Properties

What is a Hypothesis – Types, Examples and Writing Guide

Types of Hypothesis

Research Hypothesis

Null Hypothesis

Alternative Hypothesis

Directional Hypothesis

Non-directional Hypothesis

Statistical Hypothesis

Composite Hypothesis

Empirical Hypothesis

Simple Hypothesis

Complex Hypothesis

Applications of Hypothesis

How to write a Hypothesis

Identify the Research Question

Conduct a Literature Review

Determine the Variables

Formulate the Hypothesis

Write the Null Hypothesis

Refine the Hypothesis

Examples of Hypothesis

Purpose of Hypothesis

When to use Hypothesis

Characteristics of Hypothesis

Advantages of Hypothesis

Limitations of Hypothesis

About the author

Muhammad Hassan

You may also like

Data Collection – Methods Types and Examples

Delimitations in Research – Types, Examples and...

Research Process – Steps, Examples and Tips

Research Design – Types, Methods and Examples

Institutional Review Board – Application Sample...

Evaluating Research – Process, Examples and...

Understanding the Role of Hypotheses and Conclusions in Mathematical Reasoning

More Answers:

Formula for cyclic adenosine monophosphate & Its Significance

Development of a Turtle Inside its Egg

The Essential Molecule in Photosynthesis for Energy and Biomass

How the Human Body Recycles its Energy Currency

Don't Miss Out! Sign Up Now!

The Craft of Writing a Strong Hypothesis

Table of Contents

What is a Hypothesis?