representation math

Representation Theory

Representation theory is fundamental in the study of objects with symmetry. It arises in contexts as diverse as card shuffling and quantum mechanics. An early success was the work of Schur and Weyl, who computed the representation theory of the symmetric and unitary groups; the answer is closely related to the classical theory of symmetric functions and deeper study leads to intricate questions in combinatorics.

More recently, methods from geometry and topology have greatly enhanced our understanding of these questions (“geometric representation theory”). The study of affine Lie algebras and quantum groups has brought many new ideas and viewpoints, and representation theory now furnishes a basic language for other fields, including the modern theory of automorphic forms.

All of these aspects are studied by Stanford faculty.  Topics of recent seminars include combinatorial representation theory as well as quantum groups.

© Stanford University . Stanford , California 94305 .

Publications — Over 100 years of publishing excellence

• Book Author Resources
• Submit a Book Proposal
• AMS Rights, Licensing, and Permissions
• Open Math Notes
• Frequently asked questions
• Member Journals
• Research Journals
• Translation Journals
• Distributed Journals
• Open Access Journals
• Guidelines and Policies
• Journal Author Resources

Librarian Resources

• eBook Collections
• COUNTER Usage Statistics
• My Subscriptions
• Subscription Information
• Licensing Information

Mathematical Reviews/MathSciNet®

• MathSciNet ®
• Reviewer Home
• MathSciNet ® Subscriptions

Membership — Welcome to your membership center

Join the ams, renew your membership, give a membership, individual membership.

• Member Benefits
• Member Directory
• Reciprocating Societies
• Members in Developing Countries

Institutional Membership

• Domestic Institutions
• International Institutions
• Two-Year Institutions
• Graduate Student Chapter Program

Other Member Types

• Corporate Memberships
• Associate Memberships

Meetings & Conferences — Engage with colleagues and the latest research

National meetings.

• Joint Mathematics Meetings
• Upcoming JMMs
• Previous JMMs
• Special Lectures
• Professional Enhancement Programs (PEPs)

Sectional Meetings

• Upcoming Sectionals
• Previous Sectionals
• Presenting Papers
• Hosting Sectionals

Other Meetings, Conferences & Workshops

• Mathematics Research Communities
• Education Mini-conference
• International Meetings
• Mathematics Calendar
• Short Courses
• Workshop for Department Chairs and Leaders

Meetings Resources

• Suggest a Speaker
• AMS Meetings Grants
• Submitting Abstracts
• Welcoming Environment Policy
• MathSafe – supporting safe meetings

News & Outreach — Explore news, images, posters, and mathematical essays

News from the ams.

• AMS News Releases
• Feature Stories
• Information for Journalists
• In Memory Of

Math Voices

• Feature Column
• Math in the Media
• Column on Teaching and Learning

Explorations

• Recognizing Diverse Mathematicians
• AMS Posters
• Mathematics & Music
• Mathematical Imagery
• Mathematical Moments

Professional Programs — Resources and opportunities to further your mathematical pursuits

Professional development.

• Employment Services
• Mathjobs.org
• BEGIN Career Initiative
• Mathprograms.org
• Mathematical Opportunities Database
• Research Seminars

Institutional Information and Data

• Annual Survey of the Mathematical and Statistical Sciences
• CBMS Survey
• Other Sources of Data
• Directory of Institutions in the Mathematical Sciences
• Professional Directory

Grants & Support

• AMS-Simons Grants for PUI Faculty
• Travel Grants
• Fellowships & Scholarships
• Epsilon Fund
• Child Care Grants

Awards & Recognition

• AMS Prizes & Awards
• Fellows of the AMS

Education — Resources to support advanced mathematics teaching and learning

For students.

• Information for Undergraduate and High School Students
• Research Experiences for Undergraduates (REUs)
• Considering Grad School
• Find Grad Programs
• Applying to Grad School
• What do Mathematicians Do?

For Teachers

• Teaching Online
• Teaching Resources
• Inclusive Classrooms
• Assessing Student Learning
• Education Webinars

For Department Leaders & Mentors

• Information for Department Leaders
• paraDIGMS (Diversity in Graduate Mathematical Sciences)

Government Relations — Advocating for the mathematical sciences

Elevating mathematics in congress.

• Our Mission
• Letters, Statements, & Legislation
• Congressional Briefings

Legislative Priorities

• Federal Issues of Concern
• Federal Budget Process

Get Involved

• Advocacy Resources
• Take Action

DC-Based Fellowships

• Congressional Fellowship
• Mass Media Fellowship
• Catalyzing Advocacy in Science & Engineering (CASE) Fellowship

Giving to the AMS — Your gifts make great things happen for mathematics   Make a Gift

What you can support.

• The 2020 Fund
• Next Generation Fund
• Birman Fellowship for Women Scholars
• JMM Child Care Grants
• MathSciNet for Developing Countries

Create a Legacy

• Make a Tribute Gift
• Create a Permanent Fund
• Establish a Prize, Award or Fellowship
• Bequests and Charitable Estate Planning

Honoring Your Gift

• Donor Stories
• Donor Wall of Honor
• Thomas S. Fiske Society
• AMS Contributors Society
• AMS Gardens

Giving Resources

• AMS Development Committee
• AMS Gift Acceptance Policy

About the AMS — Advancing research. Connecting the mathematics community.

Our organization.

• Executive Staff
• Equity, Diversity, & Inclusion
• Jobs at AMS
• Customer Service

Our Governance

• Board of Trustees
• Executive Committee

Governance Operations

• Calendar of Meetings
• Policy Statements & Guidelines

Representation Theory

Published by the American Mathematical Society since 1997, this electronic-only journal is devoted to research in representation theory and seeks to maintain a high standard for exposition as well as for mathematical content. All articles are freely available to all readers and with no publishing fees for authors.

ISSN 1088-4165

The 2020 MCQ for Representation Theory is 0.71 . What is MCQ? The Mathematical Citation Quotient (MCQ) measures journal impact by looking at citations over a five-year period. Subscribers to MathSciNet may click through for more detailed information.

• All volumes

Jump to navigation

• Contact/Visit
• RCF Support

You are here

Representation theory.

The representation theory faculty work on a range of problems related to Lie algebras and algebraic groups, using techniques drawn from combinatorics, geometry, and algebra. An algebraic group is an algebraic variety which is also a group and its tangent space at the identity comes with a Lie algebra structure. Representation theory is concerned with understanding how to embed the group (or the Lie algebra) into the set of matrices. Our research interests involve studying the rich collection of algebraic and geometric structures related to these embeddings, over the complex numbers and other fields. Such structures include Schubert varieties, affine and double affine Hecke algebras, symplectic reflection algebras, Springer fibers, nilpotent orbits, and affine Grassmannians, to name a few.

The Representation Theory Seminar is our main research venue, and most members also attend the Valley Geometry Seminar . In recent years, we have organized reading courses and special seminars geared specifically toward graduate students, including ones on Kazhdan-Lusztig polynomials, cluster algebras, quiver varieties and Springer theory.

The diagram on the right shows Kazhdan-Lusztig cells in the affine reflection group of type G 2 .

Department of Mathematics and Statistics

• Follow us on Instagram
• Find us on Facebook
• Follow us on Twitter
• Subscribe to us on YouTube
• Make a Gift

Encyclopedia of Mathematics Education pp 566–572 Cite as

Mathematical Representations

• Gerald A. Goldin 2  
• Reference work entry
• First Online: 01 January 2020

707 Accesses

6 Citations

Definitions

As most commonly interpreted in education, mathematical representations are visible or tangible productions – such as diagrams, number lines, graphs, arrangements of concrete objects or manipulatives, physical models, written words, mathematical expressions, formulas and equations, or depictions on the screen of a computer or calculator – that encode, stand for, or embody mathematical ideas or relationships. Such a production is sometimes called an inscription when the intent is to focus on a specific instance without referring, even tacitly, to any interpretation of it. To call something a representation thus includes reference to some meaning or signification it is taken to have. Such representations are called external – i.e., they are external to the individual who produced them and accessible to others for observation, discussion, interpretation, and/or manipulation. Spoken language, interjections, gestures, facial expressions, movements, and postures may sometimes...

• Cognitive configurations
• Concrete embodiments
• External representations
• Inscriptions
• Interpretation
• Internal representations
• Manipulatives
• Neuroscience
• Productions
• Representational systems
• Signification
• Symbolization
• Visualization

This is a preview of subscription content, log in via an institution .

Buying options

• Available as PDF
• Read on any device
• Instant download
• Own it forever
• Available as EPUB and PDF
• Durable hardcover edition
• Dispatched in 3 to 5 business days
• Free shipping worldwide - see info

Tax calculation will be finalised at checkout

Purchases are for personal use only

Anderson C, Scheuer N, Pérez Echeverría MP, Teubal EV (eds) (2009) Representational systems and practices as learning tools. Sense, Rotterdam

Google Scholar  

Bruner JS (1966) Toward a theory of instruction. The Belknap Press – Harvard University Press, Cambridge, MA

Common Core State Standards Initiative (2018) Preparing America’s students for success. Retrieved June 2018 from http://www.corestandards.org/

Cuoco AA, Curcio FR (2001) The roles of representation in school mathematics: NCTM 2001 yearbook. National Council of Teachers of Mathematics, Reston

Davis RB (1984) Learning mathematics: the cognitive science approach to mathematics education. Ablex, Norwood

Duval R (2006) A cognitive analysis of problems of comprehension in a learning of mathematics. Educ Stud Math 61:103–131

Article   Google Scholar  

Goldin GA (1998) Representational systems, learning, and problem solving in mathematics. J Math Behav 17:137–165

Goldin GA (2008) Perspectives on representation in mathematical learning and problem solving. In: English LD (ed) Handbook of international research in mathematics education, 2nd edn. Routledge – Taylor and Francis, London, pp 176–201

Goldin GA, Janvier, C (eds) (1998) Representations and the psychology of mathematics education: parts I and II (special issues). J Math Behav 17(1 & 2)

Goldin GA, Kaput JJ (1996) A joint perspective on the idea of representation in learning and doing mathematics. In: Steffe L, Nesher P, Cobb P, Goldin GA, Greer B (eds) Theories of mathematical learning. Erlbaum, Hillsdale, pp 397–430

Gravemeijer K, Doorman M, Drijvers P (2010) Symbolizing and the development of meaning in computer-supported algebra education. In: Verschaffel L, De Corte E, de Jong T, Elen J (eds) Use of representations in reasoning and problem solving: analysis and improvement. Routledge – Taylor and Francis, London, pp 191–208

Heinze A, Star JR, Verschaffel L (2009) Flexible and adaptive use of strategies and representations in mathematics education. ZDM 41:535–540

Hitt F (ed) (2002) Representations and mathematics visualization. Departamento de Matemática Educativa del Cinvestav – IPN, México

Janvier C (ed) (1987) Problems of representation in the teaching and learning of mathematics. Erlbaum, Hillsdale

Kaput J, Noss R, Hoyles C (2002) Developing new notations for a learnable mathematics in the computational era. In: English LD (ed) Handbook of international research in mathematics education. Erlbaum, Mahwah, pp 51–75

Lesh RA, Doerr HM (eds) (2003) Beyond constructivism: models and modeling perspectives on mathematics problem solving, learning, and teaching. Erlbaum, Mahwah

McClelland JL, Mickey K, Hansen S, Yuan A, Lu Q (2016) A parallel-distributed processing approach to mathematical cognition. Manuscript, Stanford University. Retrieved June 2018 from https://stanford.edu/~jlmcc/papers/

Moreno-Armella L, Sriraman B (2010) Symbols and mediation in mathematics education. In: Sriraman B, English L (eds) Advances in mathematics education: seeking new frontiers. Springer, Berlin, pp 213–232

Moreno-Armella L, Hegedus SJ, Kaput JJ (2008) From static to dynamic mathematics: historical and representational perspectives. Educ Stud Math 68:99–111

National Council of Teachers of Mathematics (2000) Principles and standards for school mathematics. NCTM, Reston

Newell A, Simon HA (1972) Human problem solving. Prentice-Hall, Englewood Cliffs

Novack MA, Congdon EL, Hermani-Lopez N, Goldin-Meadow S (2014) From action to abstraction: using the hands to learn math. Psychol Sci 25:903–910

Palmer SE (1978) Fundamental aspects of cognitive representation. In: Rosch E, Lloyd B (eds) Cognition and categorization. Erlbaum, Hillsdale, pp 259–303

Roth W-M (ed) (2009) Mathematical representation at the interface of body and culture. Information Age, Charlotte

Skemp RR (ed) (1982) Understanding the symbolism of mathematics (special issue). Visible Language 26(3)

van Garderen D, Scheuermann A, Poch A, Murray MM (2018) Visual representation in mathematics: special education teachers’ knowledge and emphasis for instruction. Teach Educ Spec Educ 41:7–23

Download references

Author information

Authors and affiliations.

Graduate School of Education, Rutgers University, New Brunswick, NJ, USA

Gerald A. Goldin

You can also search for this author in PubMed   Google Scholar

Corresponding author

Correspondence to Gerald A. Goldin .

Editor information

Editors and affiliations.

Department of Education, Centre for Mathematics Education, London South Bank University, London, UK

Stephen Lerman

Section Editor information

Department of Science Teaching, The Weizmann Institute of Science, Rehovot, Israel

Ruhama Even

Rights and permissions

Reprints and permissions

Copyright information

© 2020 Springer Nature Switzerland AG

About this entry

Cite this entry.

Goldin, G.A. (2020). Mathematical Representations. In: Lerman, S. (eds) Encyclopedia of Mathematics Education. Springer, Cham. https://doi.org/10.1007/978-3-030-15789-0_103

Download citation

DOI : https://doi.org/10.1007/978-3-030-15789-0_103

Published : 23 February 2020

Publisher Name : Springer, Cham

Print ISBN : 978-3-030-15788-3

Online ISBN : 978-3-030-15789-0

eBook Packages : Education Reference Module Humanities and Social Sciences Reference Module Education

Share this entry

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

• Publish with us

Policies and ethics

• Find a journal
• Track your research

Initial Thoughts

Perspectives & resources, what is high-quality mathematics instruction and why is it important.

• Page 1: The Importance of High-Quality Mathematics Instruction
• Page 2: A Standards-Based Mathematics Curriculum
• Page 3: Evidence-Based Mathematics Practices

What evidence-based mathematics practices can teachers employ?

• Page 4: Explicit, Systematic Instruction

Page 5: Visual Representations

• Page 6: Schema Instruction
• Page 7: Metacognitive Strategies
• Page 8: Effective Classroom Practices
• Page 9: References & Additional Resources
• Page 10: Credits

Research Shows

• Students who use accurate visual representations are six times more likely to correctly solve mathematics problems than are students who do not use them. However, students who use inaccurate visual representations are less likely to correctly solve mathematics problems than those who do not use visual representations at all. (Boonen, van Wesel, Jolles, & van der Schoot, 2014)
• Students with a learning disability (LD) often do not create accurate visual representations or use them strategically to solve problems. Teaching students to systematically use a visual representation to solve word problems has led to substantial improvements in math achievement for students with learning disabilities. (van Garderen, Scheuermann, & Jackson, 2012; van Garderen, Scheuermann, & Poch, 2014)
• Students who use visual representations to solve word problems are more likely to solve the problems accurately. This was equally true for students who had LD, were low-achieving, or were average-achieving. (Krawec, 2014)

Visual representations are flexible; they can be used across grade levels and types of math problems. They can be used by teachers to teach mathematics facts and by students to learn mathematics content. Visual representations can take a number of forms. Click on the links below to view some of the visual representations most commonly used by teachers and students.

How does this practice align?

High-leverage practice (hlp).

• HLP15 : Provide scaffolded supports

CCSSM: Standards for Mathematical Practice

• MP1 : Make sense of problems and persevere in solving them.

Number Lines

Definition : A straight line that shows the order of and the relation between numbers.

Common Uses : addition, subtraction, counting

Strip Diagrams

Definition : A bar divided into rectangles that accurately represent quantities noted in the problem.

Common Uses : addition, fractions, proportions, ratios

Definition : Simple drawings of concrete or real items (e.g., marbles, trucks).

Common Uses : counting, addition, subtraction, multiplication, division

Graphs/Charts

Definition : Drawings that depict information using lines, shapes, and colors.

Common Uses : comparing numbers, statistics, ratios, algebra

Graphic Organizers

Definition : Visual that assists students in remembering and organizing information, as well as depicting the relationships between ideas (e.g., word webs, tables, Venn diagrams).

Common Uses : algebra, geometry

Before they can solve problems, however, students must first know what type of visual representation to create and use for a given mathematics problem. Some students—specifically, high-achieving students, gifted students—do this automatically, whereas others need to be explicitly taught how. This is especially the case for students who struggle with mathematics and those with mathematics learning disabilities. Without explicit, systematic instruction on how to create and use visual representations, these students often create visual representations that are disorganized or contain incorrect or partial information. Consider the examples below.

Elementary Example

Mrs. Aldridge ask her first-grade students to add 2 + 4 by drawing dots.

Notice that Talia gets the correct answer. However, because Colby draws his dots in haphazard fashion, he fails to count all of them and consequently arrives at the wrong solution.

High School Example

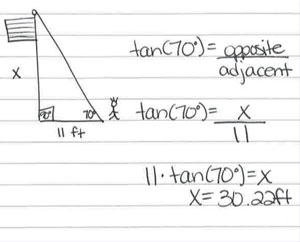
Mr. Huang asks his students to solve the following word problem:

The flagpole needs to be replaced. The school would like to replace it with the same size pole. When Juan stands 11 feet from the base of the pole, the angle of elevation from Juan’s feet to the top of the pole is 70 degrees. How tall is the pole?

Compare the drawings below created by Brody and Zoe to represent this problem. Notice that Brody drew an accurate representation and applied the correct strategy. In contrast, Zoe drew a picture with partially correct information. The 11 is in the correct place, but the 70° is not. As a result of her inaccurate representation, Zoe is unable to move forward and solve the problem. However, given an accurate representation developed by someone else, Zoe is more likely to solve the problem correctly.

Manipulatives

Some students will not be able to grasp mathematics skills and concepts using only the types of visual representations noted in the table above. Very young children and students who struggle with mathematics often require different types of visual representations known as manipulatives. These concrete, hands-on materials and objects—for example, an abacus or coins—help students to represent the mathematical idea they are trying to learn or the problem they are attempting to solve. Manipulatives can help students develop a conceptual understanding of mathematical topics. (For the purpose of this module, the term concrete objects refers to manipulatives and the term visual representations refers to schematic diagrams.)

It is important that the teacher make explicit the connection between the concrete object and the abstract concept being taught. The goal is for the student to eventually understand the concepts and procedures without the use of manipulatives. For secondary students who struggle with mathematics, teachers should show the abstract along with the concrete or visual representation and explicitly make the connection between them.

A move from concrete objects or visual representations to using abstract equations can be difficult for some students. One strategy teachers can use to help students systematically transition among concrete objects, visual representations, and abstract equations is the Concrete-Representational-Abstract (CRA) framework.

If you would like to learn more about this framework, click here.

Concrete-Representational-Abstract Framework

• Concrete —Students interact and manipulate three-dimensional objects, for example algebra tiles or other algebra manipulatives with representations of variables and units.
• Representational — Students use two-dimensional drawings to represent problems. These pictures may be presented to them by the teacher, or through the curriculum used in the class, or students may draw their own representation of the problem.
• Abstract — Students solve problems with numbers, symbols, and words without any concrete or representational assistance.

CRA is effective across all age levels and can assist students in learning concepts, procedures, and applications. When implementing each component, teachers should use explicit, systematic instruction and continually monitor student work to assess their understanding, asking them questions about their thinking and providing clarification as needed. Concrete and representational activities must reflect the actual process of solving the problem so that students are able to generalize the process to solve an abstract equation. The illustration below highlights each of these components.

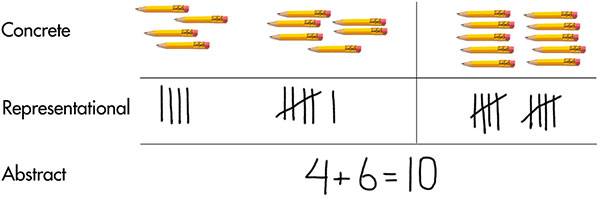
For Your Information

One promising practice for moving secondary students with mathematics difficulties or disabilities from the use of manipulatives and visual representations to the abstract equation quickly is the CRA-I strategy . In this modified version of CRA, the teacher simultaneously presents the content using concrete objects, visual representations of the concrete objects, and the abstract equation. Studies have shown that this framework is effective for teaching algebra to this population of students (Strickland & Maccini, 2012; Strickland & Maccini, 2013; Strickland, 2017).

Kim Paulsen discusses the benefits of manipulatives and a number of things to keep in mind when using them (time: 2:35).

Kim Paulsen, EdD Associate Professor, Special Education Vanderbilt University

View Transcript

Transcript: Kim Paulsen, EdD

Manipulatives are a great way of helping kids understand conceptually. The use of manipulatives really helps students see that conceptually, and it clicks a little more with them. Some of the things, though, that we need to remember when we’re using manipulatives is that it is important to give students a little bit of free time when you’re using a new manipulative so that they can just explore with them. We need to have specific rules for how to use manipulatives, that they aren’t toys, that they really are learning materials, and how students pick them up, how they put them away, the right time to use them, and making sure that they’re not distracters while we’re actually doing the presentation part of the lesson. One of the important things is that we don’t want students to memorize the algorithm or the procedures while they’re using the manipulatives. It really is just to help them understand conceptually. That doesn’t mean that kids are automatically going to understand conceptually or be able to make that bridge between using the concrete manipulatives into them being able to solve the problems. For some kids, it is difficult to use the manipulatives. That’s not how they learn, and so we don’t want to force kids to have to use manipulatives if it’s not something that is helpful for them. So we have to remember that manipulatives are one way to think about teaching math.

I think part of the reason that some teachers don’t use them is because it takes a lot of time, it takes a lot of organization, and they also feel that students get too reliant on using manipulatives. One way to think about using manipulatives is that you do it a couple of lessons when you’re teaching a new concept, and then take those away so that students are able to do just the computation part of it. It is true we can’t walk around life with manipulatives in our hands. And I think one of the other reasons that a lot of schools or teachers don’t use manipulatives is because they’re very expensive. And so it’s very helpful if all of the teachers in the school can pool resources and have a manipulative room where teachers can go check out manipulatives so that it’s not so expensive. Teachers have to know how to use them, and that takes a lot of practice.

• Skip to main content

Welcome, Fellow Math Enthusiast! I’m so happy you’re here!

• Counting & Cardinality
• Addition & Subtraction
• Multiplication & Division
• Place Value & Base Ten
• Measurement & Data
• Geometry & Fractions
• Vocabulary & Discourse
• Math Manipulatives
• Classroom Management
• Classroom Organization
• Holidays & Seasonal
• Social-Emotional Learning
• Privacy Policy
• Terms of Use
• SHOP RESOURCES
• BECOME A MEMBER
• Search this website

Teaching with Jillian Starr

teaching little stars to shine brightly

FREE Number Talks

First grade teachers, access 20 FREE Number Talk Prompts to enhance your place value unit and get your students engaged in conversation.

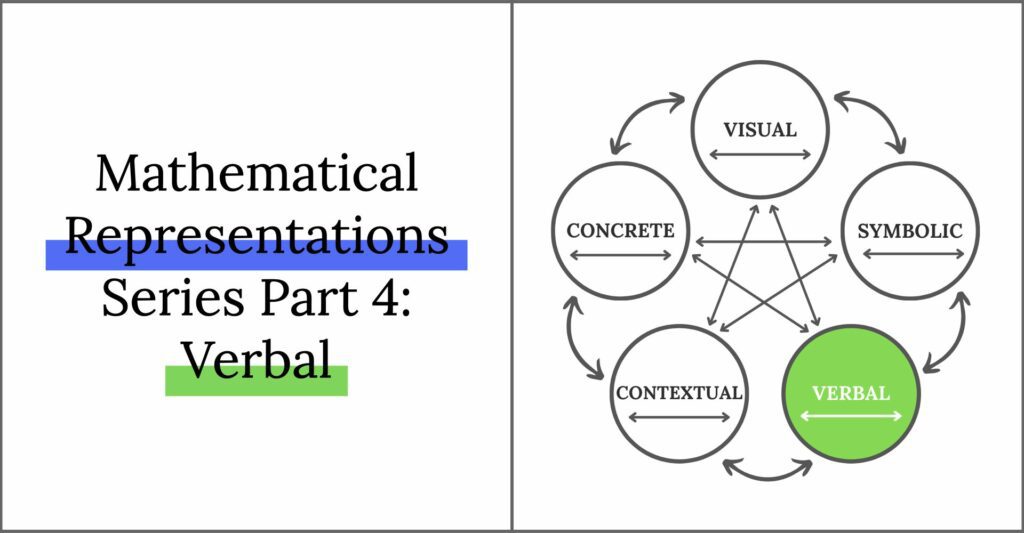
Mathematical Representations Series Part 4: Verbal Representation

Welcome back to our deep dive into mathematical representations! Today, we are taking a look at symbolic representations and how we can translate between symbolic, concrete, and visual representations. First, let’s do a two-sentence recap of this series so far:

We have already focused on concrete representations and the immense value of manipulatives, the range of visual representations we want to encourage with our students, and how we can use numerals and operations to represent thinking symbolically . We are centering our conversation around Lesh’s Translation Model, which encompasses the range of ways we represent our thinking, and stresses the importance of making connections between representations.

Today we are talking about verbal representations. While it’s an essential form of representation for our students, it is often less discussed. This is likely due to the fact that it is not explicitly called out in the Concrete-Pictorial Abstract model . This is just another reason why I love introducing teachers to Lesh’s translation model alongside the CPA (often called CRA) model.

Verbal Representation

The language we use to communicate our thoughts and ideas is another equally important representation. This can be oral, written, signed, or any way that a student would look to communicate language. James Heddens writes that students “need to be given opportunities to verbalize their thought processes: verbal interaction with peers will help learners clarify their own thinking.”

If we go back to our previous examples from concrete, visual, and abstract thinking, we have a student with five yellow counters and four red counters. The student then sketched their counters and wrote the number sentence 5+4=9 on their paper.

So how does verbal representation come into play? Perhaps after the activity, a student shows you their sketch of the counters. When you ask them about their drawing, they may share “I had nine counters. Four of them were red and five of them were yellow, and that makes nine.” That statement is a verbal representation of the concept. They have also just translated their visual representation to a verbal representation.

Connecting Two Verbal Representations

If wanted, we could take it a step further by asking the student to write their thoughts down. This will require the student to revisit their thoughts communicated orally and condense them into a written description, like “Four counters and five counters make nine counters.” This extra step of condensing their language into a second form, allowed students to connect two verbal representations. WOW!

Verbal representation is essential to our work, especially in the early grades. Our students who may not have the ability to write words or numbers will often communicate their understanding orally. This NEEDS to be a part of the discussion when we talk about deepening student understanding, and it’s a huge reason why I make sure to consider Lesh’s Translation Model in addition to the Concrete-Pictorial-Abstract model.

What’s Up Next?

This series is going to dive deep into each of the representations discussed in Lesh’s Translation Model, and then we are going to put it all together so we can make a big impact on your math teaching this year.

If you missed Part One about Concrete Representations , Part Two about Visual Representations , or Part Three about Symbolic Representations , check them out so you have all of the info you need before we move on!

Math Vocabulary Resources

You May Also Enjoy These Posts:

Reader Interactions

Leave a comment.

Your email address will not be published. Required fields are marked *

This site uses Akismet to reduce spam. Learn how your comment data is processed .

Ready to go deeper?

JOIN MEANINGFUL MATH

hello I'm Jillian

I’m so happy you’re here. I want every child to feel confident in their math abilities, and that happens when every teacher feels confident in their ability to teach math.

In my fifteen years of teaching, I sought every opportunity to learn more about teaching math. I wanted to know HOW students develop math concepts, just like I had been taught how students learn to read. I want every teacher to experience the same math transformation I did, and have the confidence to teach any student that steps foot in their classroom. I’m excited to be alongside you in your math journey!

Follow Me on Instagram!

Department of Mathematics, University of California San Diego

****************************

Math 209: Number Theory Seminar

Claus sorensen, uc san diego, projective smooth representations mod $p$.

This talk will be colloquial and geared towards people from other fields. I will talk about smooth mod $p$ representations of $p$-adic Lie groups. In stark contrast to the complex case, these categories typically do not have any (nonzero) projective objects. For reductive groups this is a byproduct of a stronger result on the derived functors of smooth induction. The talk is based on joint work with Peter Schneider.

April 11, 2024

Apm 6402 and online (see  https://www.math.ucsd.edu/~nts / ).

9500 Gilman Drive, La Jolla, CA 92093-0112

(858) 534-3590

Help | Advanced Search

Mathematics > Representation Theory

Title: on tensor products of representations of lie superalgebras.

Abstract: We consider typical finite dimensional complex irreducible representations of a basic classical simple Lie superalgebra, and give a sufficient condition on when unique factorization of finite tensor products of such representations hold. We also prove unique factorization of tensor products of singly atypical finite dimensional irreducible modules for $\mathfrak{sl}(m+1,n+1)$, $\mathfrak{osp}(2,2n)$, $G(3)$ and $F(4)$ under an additional assumption. This result is a Lie superalgebra analogue of Rajan's fundamental result \cite{MR2123935} on unique factorization of tensor products for finite dimensional complex simple Lie algebras.

Submission history

Access paper:.

• HTML (experimental)
• Other Formats

References & Citations

• Google Scholar
• Semantic Scholar

BibTeX formatted citation

Bibliographic and Citation Tools

Code, data and media associated with this article, recommenders and search tools.

• Institution

arXivLabs: experimental projects with community collaborators

arXivLabs is a framework that allows collaborators to develop and share new arXiv features directly on our website.

Both individuals and organizations that work with arXivLabs have embraced and accepted our values of openness, community, excellence, and user data privacy. arXiv is committed to these values and only works with partners that adhere to them.

Have an idea for a project that will add value for arXiv's community? Learn more about arXivLabs .

Department of Mathematics, University of California San Diego

****************************

Math Colloquium

Subha maity, university of michigan, department of statistics, investigations of algorithmic biases caused by underrepresentation of minority groups.

The problem of algorithmic bias, where machine learning algorithms reflect biases that are prevalent in their training datasets, is widely recognized as a major concern. In this talk, I will discuss two of my projects related to algorithmic biases that are caused by underrepresentation of minority groups. In the first project, we demonstrate that when learning representations from standard contrastive learning methods, the representations of minority groups merge with the representations of certain similar majority groups. We refer to this phenomenon as representation harm and demonstrate that it leads to allocation harms in downstream classification tasks. In the second project, we investigate whether enforcing group fairness is aligned with improving model performance. In light of the long-held belief that enforcing fairness comes at the cost of reduced model performance, we present an alternative perspective on the problem. In cases where the machine bias is due to the underrepresentation of minority groups, we show that enforcing fairness is often in line with improving model performance on a balanced test dataset. Furthermore, we derive necessary and sufficient conditions for such an alignment. 

Host: Jelena Bradic

January 22, 2024

9500 Gilman Drive, La Jolla, CA 92093-0112

(858) 534-3590