Curriculum / Math / 10th Grade / Unit 4: Right Triangles and Trigonometry / Lesson 10

Right Triangles and Trigonometry
Lesson 10 of 19
Criteria for Success
Tips for teachers, anchor problems.
- Problem Set
Target Task
Additional practice.
Solve for missing sides of a right triangle given the length of one side and measure of one angle.
Common Core Standards
Core standards.
The core standards covered in this lesson
Similarity, Right Triangles, and Trigonometry
G.SRT.C.8 — Use trigonometric ratios and the Pythagorean Theorem to solve right triangles in applied problems. Modeling is best interpreted not as a collection of isolated topics but in relation to other standards. Making mathematical models is a Standard for Mathematical Practice, and specific modeling standards appear throughout the high school standards indicated by a star symbol (★). The star symbol sometimes appears on the heading for a group of standards; in that case, it should be understood to apply to all standards in that group.
Foundational Standards
The foundational standards covered in this lesson
8.G.B.7 — Apply the Pythagorean Theorem to determine unknown side lengths in right triangles in real-world and mathematical problems in two and three dimensions.
The essential concepts students need to demonstrate or understand to achieve the lesson objective
- Given any one side and any one angle measure, determine the rest of the side lengths and missing angle measures of a right triangle.
- Solve triangles using the Pythagorean theorem, similarity relationships, and trigonometric ratios.
- Understand that trigonometric ratios and the Pythagorean theorem can only be used to solve RIGHT triangles.
Suggestions for teachers to help them teach this lesson
- In later lessons, students in advanced courses will learn the Law of Sines and the Law of Cosines. Criteria for Success #3 is necessary to include due to students appropriately using the trigonometric ratios in non-right triangles before they know about the Law of Sines and Law of Cosines.
- Students should use their calculators with trigonometric ratios in this lesson. Ensure that students are familiar with how to use their calculators to calculate the trigonometric ratios.
Unlock features to optimize your prep time, plan engaging lessons, and monitor student progress.
Problems designed to teach key points of the lesson and guiding questions to help draw out student understanding
Below is a triangle with angle measure 51° and side length of measure 16.5. Find the missing side lengths and angle measures.
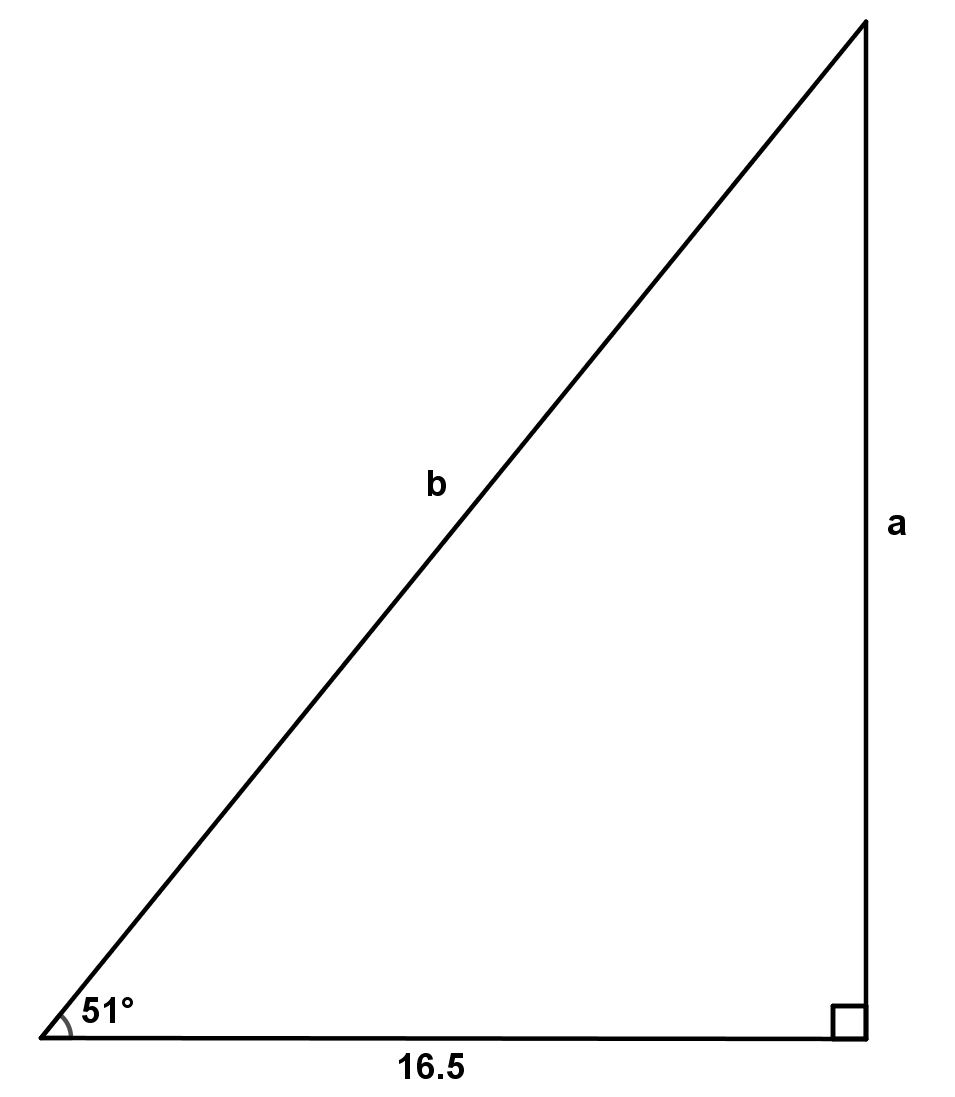
Guiding Questions
A shipmate set a boat to sail exactly 27° NE from the dock. After traveling 120 miles, the shipmate realized he had misunderstood the instructions from the captain; he was supposed to set sail going directly east! The boat is now due north of his destination.
a) How many miles would the boat have traveled if the shipmate followed the directions of the captain? b) How many miles is the boat off course after traveling for 120 miles at 27° NE?
Geometry > Module 2 > Topic E > Lesson 28 of the New York State Common Core Mathematics Curriculum from EngageNY and Great Minds . © 2015 Great Minds. Licensed by EngageNY of the New York State Education Department under the CC BY-NC-SA 3.0 US license. Accessed Dec. 2, 2016, 5:15 p.m..
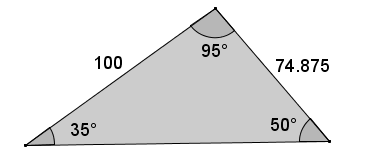
Find the base of the triangle:
A task that represents the peak thinking of the lesson - mastery will indicate whether or not objective was achieved
Given right triangle $${A{BC}}$$ with hypotenuse $${AB=8.5}$$ and $${m\angle A=55^\circ}$$ , find $${AC}$$ and $${BC}$$ to the nearest hundredth.

The following resources include problems and activities aligned to the objective of the lesson that can be used for additional practice or to create your own problem set.
- Include problems with non-right triangles as error analysis problems. Ask students to identify why they are unable to use the trigonometric ratios to find the values of the missing sides in non-right triangles.
- Include problems where right triangles are embedded in other right triangles and students need to investigate the diagram carefully to find the solution.
- Include problems where students use a trigonometric ratio of one triangle to find the missing side length of a similar triangle.
- EngageNY Mathematics Geometry > Module 2 > Topic E > Lesson 28
- JMAP G.SRT.C.8: Pythagorean Theorem
- New Visions for Public Schools Unit 4: Right Triangle Trigonometry — Big Idea 2: Sine, Cosine, and Tangent are Constant Ratios that Relate the Angles and Sides of a Right Triangle
Topic A: Right Triangle Properties and Side-Length Relationships
Define the parts of a right triangle and describe the properties of an altitude of a right triangle.
G.CO.A.1 G.SRT.B.4
Define and prove the Pythagorean theorem. Use the Pythagorean theorem and its converse in the solution of problems.
Define the relationship between side lengths of special right triangles.
G.SRT.B.4 G.SRT.B.5
Multiply and divide radicals. Rationalize the denominator.
A.SSE.A.2 N.RN.A.2
Add and subtract radicals.
Create a free account to access thousands of lesson plans.
Already have an account? Sign In
Topic B: Right Triangle Trigonometry
Define and calculate the sine of angles in right triangles. Use similarity criteria to generalize the definition of sine to all angles of the same measure.
Define and calculate the cosine of angles in right triangles. Use similarity criteria to generalize the definition of cosine to all angles of the same measure.
Derive the relationship between sine and cosine of complementary angles in right triangles, and describe sine and cosine as angle measures approach 0°, 30°, 45°, 60°, and 90°.
Describe and calculate tangent in right triangles. Describe how the value of tangent changes as the angle measure approaches 0°, 45°, and 90°.
G.SRT.C.6 G.SRT.C.7
Topic C: Applications of Right Triangle Trigonometry
Find the angle measure given two sides using inverse trigonometric functions.
Describe the relationship between slope and the tangent ratio of the angle of elevation/depression. Use the tangent ratio of the angle of elevation or depression to solve real-world problems.
Solve a modeling problem using trigonometry.
Topic D: The Unit Circle
Define angles in standard position and use them to build the first quadrant of the unit circle.
Use the first quadrant of the unit circle to define sine, cosine, and tangent values outside the first quadrant.
Topic E: Trigonometric Ratios in Non-Right Triangles
Derive the area formula for any triangle in terms of sine.
Verify algebraically and find missing measures using the Law of Sines.
Verify algebraically and find missing measures using the Law of Cosines.
Use side and angle relationships in right and non-right triangles to solve application problems.
Request a Demo
See all of the features of Fishtank in action and begin the conversation about adoption.
Learn more about Fishtank Learning School Adoption.
Contact Information
School information, what courses are you interested in, are you interested in onboarding professional learning for your teachers and instructional leaders, any other information you would like to provide about your school.

Effective Instruction Made Easy
Access rigorous, relevant, and adaptable math lesson plans for free
Solve Problems Using Trigonometric Ratios
Introduction to Trigonometry
Trigonometry (from Greek trigonon "triangle" + metron "measure")
Want to learn Trigonometry? Here is a quick summary. Follow the links for more, or go to Trigonometry Index
Trigonometry helps us find angles and distances, and is used a lot in science, engineering, video games, and more!
Right-Angled Triangle
The triangle of most interest is the right-angled triangle . The right angle is shown by the little box in the corner:
Another angle is often labeled θ , and the three sides are then called:
- Adjacent : adjacent (next to) the angle θ
- Opposite : opposite the angle θ
- and the longest side is the Hypotenuse
Why a Right-Angled Triangle?
Why is this triangle so important?
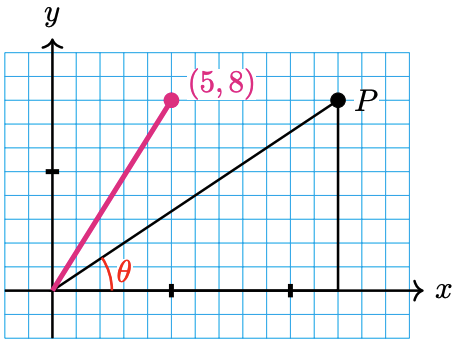
Imagine we can measure along and up but want to know the direct distance and angle:
Trigonometry can find that missing angle and distance.
Or maybe we have a distance and angle and need to "plot the dot" along and up:
Questions like these are common in engineering, computer animation and more.
And trigonometry gives the answers!
Sine, Cosine and Tangent
The main functions in trigonometry are Sine, Cosine and Tangent
They are simply one side of a right-angled triangle divided by another.
For any angle " θ ":
(Sine, Cosine and Tangent are often abbreviated to sin, cos and tan .)
Example: What is the sine of 35°?
Using this triangle (lengths are only to one decimal place):
sin(35°) = Opposite Hypotenuse = 2.8 4.9 = 0.57...
The triangle could be larger, smaller or turned around, but that angle will always have that ratio .
Calculators have sin, cos and tan to help us, so let's see how to use them:
Example: How Tall is The Tree?
We can't reach the top of the tree, so we walk away and measure an angle (using a protractor) and distance (using a laser):
- We know the Hypotenuse
- And we want to know the Opposite
Sine is the ratio of Opposite / Hypotenuse :
sin(45°) = Opposite Hypotenuse

Get a calculator, type in "45", then the "sin" key:
sin(45°) = 0.7071...
What does the 0.7071... mean? It is the ratio of the side lengths, so the Opposite is about 0.7071 times as long as the Hypotenuse.
We can now put 0.7071... in place of sin(45°):
0.7071... = Opposite Hypotenuse
And we also know the hypotenuse is 20 :
0.7071... = Opposite 20
To solve, first multiply both sides by 20:
20 × 0.7071... = Opposite
Opposite = 14.14m (to 2 decimals)
The tree is 14.14m tall
Try Sin Cos and Tan
Play with this for a while (move the mouse around) and get familiar with values of sine, cosine and tangent for different angles, such as 0°, 30°, 45°, 60° and 90°.
Also try 120°, 135°, 180°, 240°, 270° etc, and notice that positions can be positive or negative by the rules of Cartesian coordinates , so the sine, cosine and tangent change between positive and negative also.
So trigonometry is also about circles !
Unit Circle
What you just played with is the Unit Circle .
It is a circle with a radius of 1 with its center at 0.
Because the radius is 1, we can directly measure sine, cosine and tangent.
Here we see the sine function being made by the unit circle:
Note: you can see the nice graphs made by sine, cosine and tangent .
Degrees and Radians
Angles can be in Degrees or Radians . Here are some examples:
Repeating Pattern
Because the angle is rotating around and around the circle the Sine, Cosine and Tangent functions repeat once every full rotation (see Amplitude, Period, Phase Shift and Frequency ).
When we want to calculate the function for an angle larger than a full rotation of 360° (2 π radians) we subtract as many full rotations as needed to bring it back below 360° (2 π radians):
Example: what is the cosine of 370°?
370° is greater than 360° so let us subtract 360°
370° − 360° = 10°
cos(370°) = cos(10°) = 0.985 (to 3 decimal places)
And when the angle is less than zero, just add full rotations.
Example: what is the sine of −3 radians?
−3 is less than 0 so let us add 2 π radians
−3 + 2 π = −3 + 6.283... = 3.283... rad ians
sin(−3) = sin(3.283...) = −0.141 (to 3 decimal places)
Solving Triangles
Trigonometry is also useful for general triangles, not just right-angled ones .
It helps us in Solving Triangles . "Solving" means finding missing sides and angles.
Example: Find the Missing Angle "C"
Angle C can be found using angles of a triangle add to 180° :
So C = 180° − 76° − 34° = 70°
We can also find missing side lengths. The general rule is:
When we know any 3 of the sides or angles we can find the other 3 (except for the three angles case)
See Solving Triangles for more details.
Other Functions (Cotangent, Secant, Cosecant)
Similar to Sine, Cosine and Tangent, there are three other trigonometric functions which are made by dividing one side by another:
Trigonometric and Triangle Identities
And as you get better at Trigonometry you can learn these:
Enjoy becoming a triangle (and circle) expert!
Trigonometric Ratios
These lessons, with videos, examples and step-by-step solutions, help GCSE/IGCSE Maths students learn about the trigonometric ratios: sine, cosine, tangent, secant, cosecant, and cotangent.
Related Pages Trigonometric Graphs Trigonometric Functions Lessons On Trigonometry More GCSE Math Lessons Math Worksheets
The following diagram shows the six trig ratios: Sin, Cos, Tan, Sec, Csc, and Cot. Scroll down the page for more examples and solutions on the trigonometric ratios.
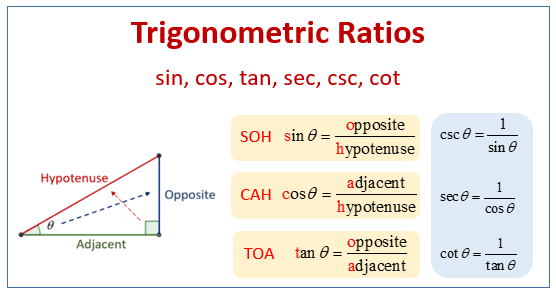
Six Trig Ratios: sin, cos, tan, csc, sec, and tan
Example: Determine the six trigonometric ratios for angle A in the right triangle.
Trigonometry - Right Angled Triangles - Naming the Sides In this tutorial you are shown how to name the sides of any right-angled triangle which is the first stage in solving a question in trigonometry.
Trigonometry - The Trig Ratios In this tutorial you are shown how the sin, cos and tan ratios compare two sides of a right-angled triangle. You need to know this before calculating lengths and angles of right-angled triangles.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.
Problems on Trigonometric Ratios
Some trigonometric solutions based problems on trigonometric ratios are shown here with the step-by-step explanation.
1. If sin θ = 8/17, find other trigonometric ratios of <θ.
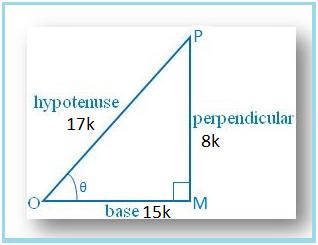
Let us draw a ∆ OMP in which ∠M = 90°.
Then sin θ = MP/OP = 8/17.
Let MP = 8k and OP = 17k, where k is positive.
By Pythagoras’ theorem, we get
Therefore, sin θ = MP/OP = 8k/17k = 8/17
cos θ = OM/OP = 15k/17k = 15/17
tan θ = Sin θ/Cos θ = (8/17 × 17/15) = 8/15
csc θ = 1/sin θ = 17/8
sec θ = 1/cos θ = 17/15 and
cot θ = 1/tan θ = 15/8.
2. If Cos A = 9/41, find other trigonometric ratios of ∠A.
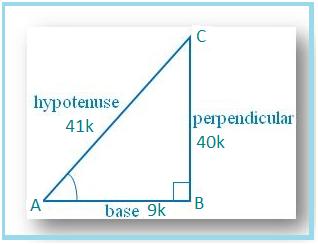
Let us draw a ∆ ABC in which ∠B = 90°.
Then cos θ = AB/AC = 9/41.
Let AB = 9k and AC = 41k, where k is positive.
Therefore, sin A = BC/AC = 40k/41k = 40/41
cos A = AB/AC = = 9k/41k = 9/41
tan A = Sin A/Cos A = (40/41 × 41/9) = 40/9
csc A = 1/sin A = 41/40
sec A = 1/cos A = 41/9 and
cot A = 1/tan A = 9/40.
3. Show that the value of sin θ and cos θ cannot be more than 1.
We know, in a right angle triangle the hypotenuse is the longest side.
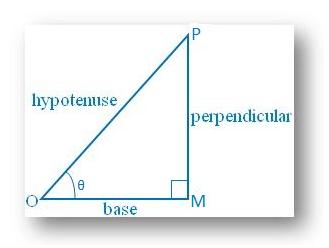
sin θ = perpendicular/hypotenuse = MP/OP < 1 since perpendicular cannot be greater than hypotenuse; sin θ cannot be more than 1.
Similarly, cos θ = base/hypotenuse = OM/OP < 1 since base cannot be greater than hypotenuse; cos θ cannot be more than 1.
4. Is that possible when A and B be acute angles, sin A = 0.3 and cos B = 0.7?
Since A and B are acute angles, 0 ≤ sin A ≤ 1 and 0 ≤ cos B ≤ 1, that means the value of sin A and cos B lies between 0 to 1. So, it is possible that sin A = 0.3 and cos B = 0.7
5. If 0° ≤ A ≤ 90° can sin A = 0.4 and cos A = 0.5 be possible?
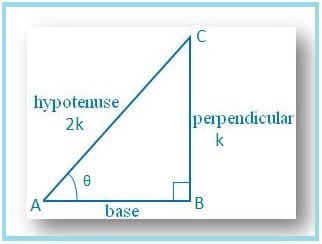
Let us draw a ∆ ABC in which ∠B = 90° and ∠BAC = θ.
Then sin θ = BC/AC = 1/2.
Let BC = k and AC = 2k, where k is positive.
= 3√3/2 - 4 × 3√3/8
= 3√3/2 - 3√3/2
Hence, (3cos θ - 4 cos<sup>3</sup> θ) = 0.
7. Show that sin α + cos α > 1 when 0 ° ≤ α ≤ 90°
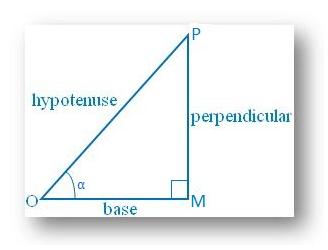
From the right triangle MOP,
Sin α = perpendicular/ hypotenuse
Cos α = base/ hypotenuse
Now, Sin α + Cos α
= perpendicular/ hypotenuse + base/ hypotenuse
= (perpendicular + base)/hypotenuse, which is > 1, Since we know that the sum of two sides of a triangle is always greater than the third side.
8. If cos θ = 3/5, find the value of (5csc θ - 4 tan θ)/(sec θ + cot θ)
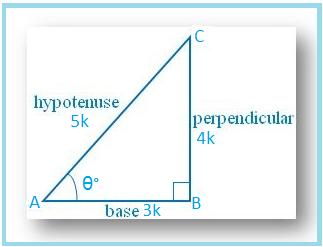
Let ∠A = θ°
Then cos θ = AB/AC = 3/5.
Let AB = 3k and AC = 5k, where k is positive.
Therefore, sec θ = 1/cos θ = 5/3
tan θ = BC/AB =4k/3k = 4/3
cot θ = 1/tan θ = 3/4 and
csc θ = AC/BC = 5k/4k = 5/4
Now (5csc θ -4 tan θ)/(sec θ + cot θ)
= (5 × 5/4 - 4 × 4/3)/(5/3 + 3/4)
= (25/4 -16/3)/(5/3 +3/4)
= 11/12 × 12/29
9. Express 1 + 2 sin A cos A as a perfect square.
1 + 2 sin A cos A
10. If sin A + cos A = 7/5 and sin A cos A =12/25, find the values of sin A and cos A.
sin A + cos A = 7/5
⇒ cos A = 7/5 - sin θ
Now from sin θ/cos θ = 12/25
We get, sin θ(7/5 - sin θ) = 12/25
or, 5 sin θ(5 sin θ - 4) - 3(5 sin θ - 4) = 0
or, (5 sin θ - 3) (5 sin θ - 4) = 0
⇒ (5 sin θ - 3) = 0 or, (5 sin θ - 4) = 0
⇒ sin θ = 3/5 or, sin θ = 4/5
When sin θ = 3/5, cos θ = 12/25 × 5/3 = 4/5
Again, when sin θ = 4/5, cos θ = 12/25 × 5/4 = 3/5
Therefore, sin θ =3/5, cos θ = 4/5
or, sin θ =4/5, cos θ = 3/5.
11. If 3 tan θ = 4, evaluate (3sin θ + 2 cos θ)/(3sin θ - 2cos θ).
Solution: Given,
3 tan θ = 4
⇒ tan θ = 4/3
(3sin θ + 2 cos θ)/(3sin θ - 2cos θ)
= (3 tan θ + 2)/(3 tan θ - 2), [dividing both numerator and denominator by cos θ]
= (3 × 4/3 + 2)/(3 × 4/3 -2), putting the value of tan θ = 4/3
12. If (sec θ + tan θ)/(sec θ - tan θ) = 209/79, find the value of θ.
Solution: (sec θ + tan θ)/(sec θ - tan θ) = 209/79
⇒ [(sec θ + tan θ) - (sec θ - tan θ)]/[(sec θ + tan θ) + (sec θ - tan θ)] = [209 – 79]/[209 + 79], (Applying componendo and dividendo)
⇒ 2 tan θ/2 sec θ =130/288
⇒ sin θ/cos θ × cos θ = 65/144
⇒ sin θ = 65/144.
13. If 5 cot θ = 3, find the value of (5 sin θ - 3 cos θ)/(4 sin θ + 3 cos θ).
Given 5 cot θ = 3
⇒ cot θ = 3/5
Now (5 sin θ - 3 cos θ)/(4 sin θ + 3 cos θ)
= (5 - 3 cot θ)/(4 sin θ + 3 cot θ), [dividing both numerator and denominator by sin θ]
= (5 - 3 × 3/5)/(4 + 3 × 3/5)
= (5 - 9/5)/(4 + 9/5)
= (16/5 × 5/29)
⇒ sin θ(sin θ - 2) - 1(sin θ - 2) = 0
⇒ (sin θ - 2)(sin θ - 1) = 0
⇒ (sin θ - 2) = 0 or, (sin θ - 1) = 0
⇒ sin θ = 2 or, sin θ = 1
So, value of sin θ can’t be greater than 1,
Therefore sin θ = 1
Basic Trigonometric Ratios
Relations Between the Trigonometric Ratios
Reciprocal Relations of Trigonometric Ratios
Trigonometrical Identity
Problems on Trigonometric Identities
Elimination of Trigonometric Ratios
Eliminate Theta between the equations
Problems on Eliminate Theta
Trig Ratio Problems
Proving Trigonometric Ratios
Trig Ratios Proving Problems
Verify Trigonometric Identities
- 10th Grade Math
From Problems on Trigonometric Ratios to HOME PAGE
New! Comments
Didn't find what you were looking for? Or want to know more information about Math Only Math . Use this Google Search to find what you need.
- Preschool Activities
- Kindergarten Math
- 1st Grade Math
- 2nd Grade Math
- 3rd Grade Math
- 4th Grade Math
- 5th Grade Math
- 6th Grade Math
- 7th Grade Math
- 8th Grade Math
- 9th Grade Math
- 11 & 12 Grade Math
- Concepts of Sets
- Probability
- Boolean Algebra
- Math Coloring Pages
- Multiplication Table
- Cool Maths Games
- Math Flash Cards
- Online Math Quiz
- Math Puzzles
- Binary System
- Math Dictionary
- Conversion Chart
- Homework Sheets
- Math Problem Ans
- Free Math Answers
- Printable Math Sheet
- Funny Math Answers
- Employment Test
- Math Patterns
- Link Partners
- Privacy Policy

Recent Articles
Multiplication by Ten, Hundred and Thousand |Multiply by 10, 100 &1000
Mar 29, 24 06:35 PM


Properties of Multiplication | Multiplicative Identity | Whole Numbers
Mar 29, 24 05:08 PM

Multiplication of a Number by a 3-Digit Number |3-Digit Multiplication
Mar 28, 24 06:33 PM

Multiply a Number by a 2-Digit Number | Multiplying 2-Digit by 2-Digit
Mar 27, 24 05:21 PM

Multiplication by 1-digit Number | Multiplying 1-Digit by 4-Digit
Mar 26, 24 04:14 PM
© and ™ math-only-math.com. All Rights Reserved. 2010 - 2024.

Want to create or adapt books like this? Learn more about how Pressbooks supports open publishing practices.
CHAPTER 9 Trigonometry
9.2 Solve Applications: Sine, Cosine and Tangent Ratios.
Learning Objectives
By the end of this section, you will be able to:
- Find missing side of a right triangle using sine, cosine, or tangent ratios
- Find missing angle of a right triangle using sine, cosine, or tangent ratios
- Solve applications using right angle trigonometry
Sine, Cosine, and Tangent Ratios
We know that any right triangle has three sides and a right angle. The side opposite to the right angle is called the hypotenuse. The other two angles in a right triangle are acute angles (with a measure less than 90 degrees). One of those angles we call reference angle and we use θ (theta) to represent it.
The hypotenuse is always the longest side of a right triangle. The other two sides are called opposite side and adjacent side. The names of those sides depends on which of the two acute angles is being used as a reference angle.
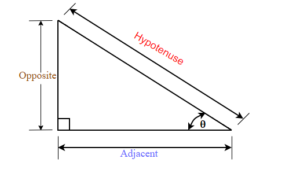
In the right triangle each side is labeled with a lowercase letter to match the uppercase letter of the opposite vertex.
Label the sides of the triangle and find the hypotenuse, opposite, and adjacent.
We labeled the sides with a lowercase letter to match the uppercase letter of the opposite vertex.
c is hypotenuse
a is opposite
b is adjacent
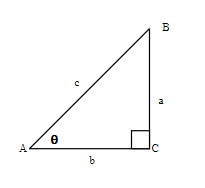
Label the sides of the triangle and find the hypotenuse, opposite and adjacent.
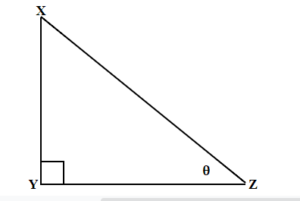
y is hypotenuse
z is opposite
x is adjacent
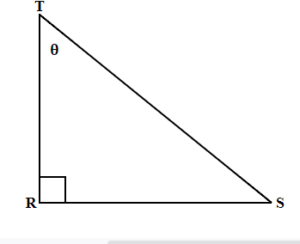
r is hypotenuse
t is opposite
s is adjacent
Trigonometric Ratios
Trigonometric ratios are the ratios of the sides in the right triangle. For any right triangle we can define three basic trigonometric ratios: sine, cosine, and tangent.
Let us refer to Figure 1 and define the three basic trigonometric ratios as:
Three Basic Trigonometric Ratios
Where θ is the measure of a reference angle measured in degrees.
Very often we use the abbreviations for sine, cosine, and tangent ratios.
Some people remember the definition of the trigonometric ratios as SOH CAH TOA.
For the given triangle find the sine, cosine and tangent ratio.
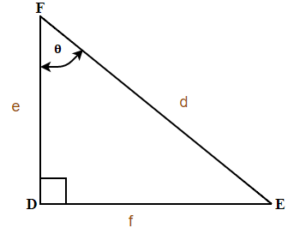
For the given triangle find the sine cosine and tangent ratio.
When calculating we will usually round the ratios to four decimal places and at the end our final answer to one decimal place unless stated otherwise.
For the given triangle find the sine, cosine and tangent ratios. If necessary round to four decimal places.
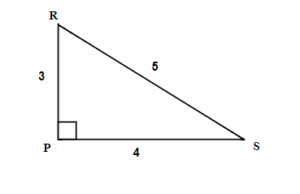
We have two possible reference angles: R an S.
Using the definitions, the trigonometric ratios for angle R are:
Using the definitions, the trigonometric ratios for angle S:
For the given triangle find the sine, cosine, and tangent ratios. If necessary round to four decimal places.
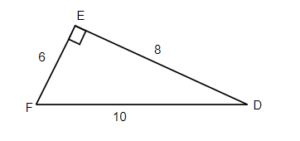
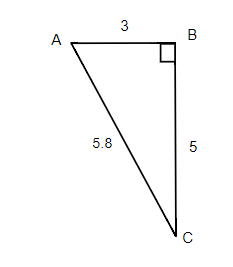
For given triangle find the sine, cosine and tangent ratios. If necessary round to four decimal places.
Now, let us use a scientific calculator to find the trigonometric ratios. Can you find the sin, cos, and tan buttons on your calculator? To find the trigonometric ratios make sure your calculator is in Degree Mode.
Using a calculator find the trigonometric ratios. If necessary, round to 4 decimal places.
Make sure your calculator is in Degree Mode.
a) Using a calculator find that sin 30° = 0.5
b) Using a calculator find that cos 45° = 0.7071 Rounded to 4 decimal places.
c) Using a calculator find that tan 60° = 1.7321 Rounded to 4 decimal places.
Find the trigonometric ratios. If necessary, round to 4 decimal places.
a) sin 60°
b) cos 30°
c) tan 45°
a) sin 60° = 0.8660
b) cos 30° = 0.8660
c) tan 45° = 1
a) sin 35°
b) cos 67°
c) tan 83°
a) sin 35° = 0.5736
b) cos 67 ° = 0.3907
c) tan 83° = 8.1443
Finding Missing Sides of a Right Triangle
In this section you will be using trigonometric ratios to solve right triangle problems. We will adapt our problem solving strategy for trigonometry applications. In addition, since those problems will involve the right triangle, it is helpful to draw it (if the drawing is not given) and label it with the given information.We will include this in the first step of the problem solving strategy for trigonometry applications.
HOW TO: Solve Trigonometry Applications
- Read the problem and make sure all the words and ideas are understood. Draw the right triangle and label the given parts.
- Identify what we are looking for.
- Label what we are looking for by choosing a variable to represent it.
- Find the required trigonometric ratio.
- Solve the ratio using good algebra techniques.
- Check the answer by substituting it back into the ratio in step 4 and by making sure it makes sense in the context of the problem.
- Answer the question with a complete sentence.
In the next few examples, having given the measure of one acute angle and the length of one side of the right triangle, we will solve the right triangle for the missing sides.
Find the missing sides. Round your final answer to two decimal places
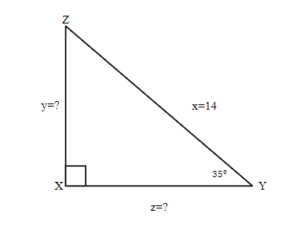
Find the missing sides. Round your final answer to one decimal place.
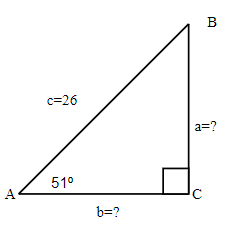
Find the missing sides. Round your final answer to one decimal place.
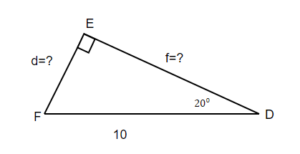
Find the hypotenuse. Round your final answer to one decimal place.
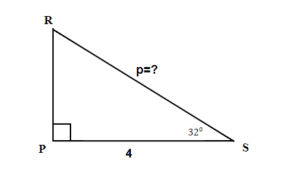
TRY IT 6.1..
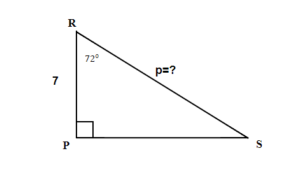
Finding Missing Angles of a Right Triangle
Sometimes we have a right triangle with only the sides given. How can we find the missing angles? To find the missing angles, we use the inverse of the trigonometric ratios. The inverse buttons sin -1 , cos -1 , and tan -1 are on your scientific calculator.
Find the angles. Round your final answer to one decimal place.
a) sin A = 0.5
b) cos B = 0.9735
c) tan C = 2.89358
Use your calculator and press the 2nd FUNCTION key and then press the SIN, COS, or TAN key
a) A = sin -1 0.5
b) B = cos -1 0.9735
c) C = tan -1 2.89358
a) sin X = 1
b) cos Y = 0.375
c) tan Z = 1.676767
a) sin C = 0
b) cos D = 0.95
c) tan F = 6.3333
In the example below we have a right triangle with two sides given. Our acute angles are missing. Let us see what the steps are to find the missing angles.
Find the missing angle X. Round your final answer to one decimal place.
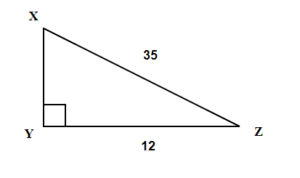
Find the missing angle Z. Round your final answer to one decimal place.

Find the missing angle A. Round your final answer to one decimal place.
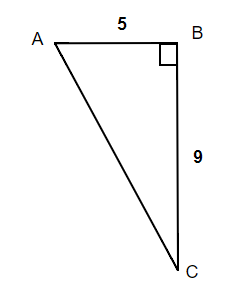
Find the missing angle C. Round your final answer to one decimal place.

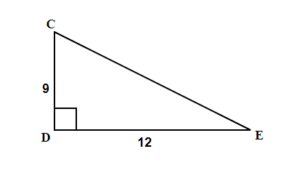
Find the missing angle E. Round your final answer to one decimal place.
Solving a Right Triangle
From the section before we know that any triangle has three sides and three interior angles. In a right triangle, when all six parts of the triangle are known, we say that the right triangle is solved.
Solve the right triangle. Round your final answer to one decimal place.
Since the sum of angles in any triangle is 180°, the measure of angle B can be easy calculated.
We solved the right triangle
TRY IT 10.1
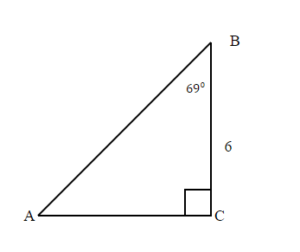
TRY IT 10.2
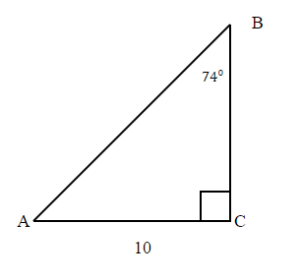
Solve the right triangle. Round to two decimal places.
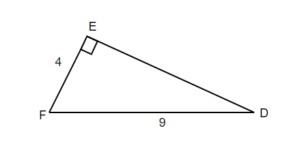
The missing angle F = 180° – 90° – 26.39° = 63.64°
TRY IT 11.1
Solve the right triangle. Round to one decimal place.
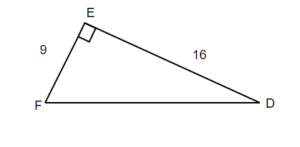
TRY IT 11.2
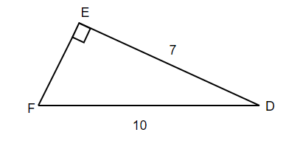
Solve Applications Using Trigonometric Ratios
In the previous examples we were able to find missing sides and missing angles of a right triangle. Now, let’s use the trigonometric ratios to solve real-life problems.
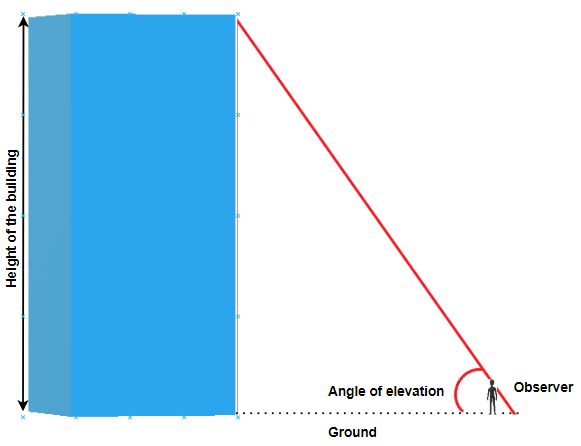
Many applications of trigonometric ratios involve understanding of an angle of elevation or angle of depression.
The angle of elevation is an angle between the horizontal line (ground) and the observer’s line of sight.
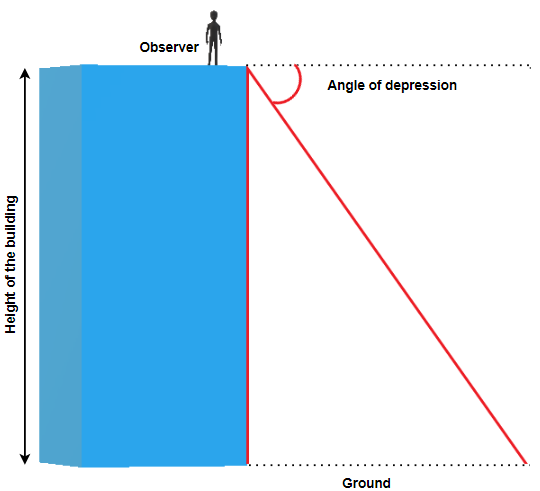
The angle of depression is the angle between horizontal line (that is parallel to the ground) and the observer’s line of sight.
James is standing 31 metres away from the base of the Harbour Centre in Vancouver. He looks up to the top of the building at a 78° angle. How tall is the Harbour Centre?
TRY IT 12.1
Nicole is standing 75 feet away from the base of the Living Shangri-La, the tallest building in British Columbia. She looks up to the top of the building at a 83.5° angle. How tall is the Living Shangri-La?
658.3 feet.
TRY IT 12.2
Kelly is standing 23 metres away from the base of the tallest apartment building in Prince George and looks at the top of the building at a 62° angle. How tall is the building?
43.3 metres
Thomas is standing at the top of the building that is 45 metres high and looks at his friend that is standing on the ground, 22 metres from the base of the building. What is the angle of depression?
TRY IT 13.1
Hemanth is standing on the top of a cliff 250 feet above the ground and looks at his friend that is standing on the ground, 40 feet from the base of the cliff. What is the angle of depression?
TRY IT 13.2
Klaudia is standing on the ground, 25 metres from the base of the cliff and looks up at her friend on the top of a cliff 100 metres above the ground. What is the angle of elevation?
Key Concepts
- Read the problem and make sure all the words and ideas are understood. Draw the right triangle and label the given parts.
- Check the answer by substituting it back into the ratio solved in step 5 and by making sure it makes sense in the context of the problem.
Practice Makes Perfect
Label the sides of the triangle.
Use your calculator to find the given ratios. Round to four decimal places if necessary:
For the given triangles, find the sine, cosine and tangent of the θ.
For the given triangles, find the missing side. Round it to one decimal place.
For the given triangles, find the missing sides. Round it to one decimal place.
Solve the triangles. Round to one decimal place.
Introductory Algebra Copyright © 2021 by Izabela Mazur is licensed under a Creative Commons Attribution 4.0 International License , except where otherwise noted.
Share This Book

- school Campus Bookshelves
- menu_book Bookshelves
- perm_media Learning Objects
- login Login
- how_to_reg Request Instructor Account
- hub Instructor Commons
- Download Page (PDF)
- Download Full Book (PDF)
- Periodic Table
- Physics Constants
- Scientific Calculator
- Reference & Cite
- Tools expand_more
- Readability
selected template will load here
This action is not available.

11.1: The Trigonometric Ratios
- Last updated
- Save as PDF
- Page ID 122907

- Katherine Yoshiwara
- Los Angeles Pierce College
2.1 Side and Angle Relationships
Homework 2.1.
1. The sum of the angles is not \(180^{\circ}\)
3. The exterior angle is not equal to the sum of the opposite interior angles.
5. The sum of the acute angles is not \(90^{\circ}\)
7. The largest side is not opposite the largest angle.
9. The Pythagorean theorem is not satisfied.
11. \(5^2+12^2=13^2\), but the angle opposite the side of length 13 is \(85^{\circ}\).
13. \(4 < x < 16\)
15. \(0 < x < 16\)
19. \(6\sqrt{2}\)in
21. \(w = 6\sqrt{10}\)in
25. \(\sqrt{3}\)
33. The distance from \((0,0)\) to \((3,3)\) is \(3 \sqrt{2}\), and the distance from \((3,3)\) to \((6,0)\) is also \(3 \sqrt{2}\), so the triangle is isosceles. The distance from \((0,0)\) to \((6,0)\) is 6 , and \((3 \sqrt{2})^2+(3 \sqrt{2})^2=6^2\) so the triangle is a right triangle.
37. \(\alpha=30^{\circ}, \beta=60^{\circ}, h=\sqrt{3}\)
39. \(8 \sqrt{3}\) in
a \((-1,0)\) and \((1,0) ; 2\)
b \(\sqrt{(p+1)^2+q^2}\) and \(\sqrt{(p-1)^2+q^2}\)
\begin{aligned} \left(\sqrt{(p+1)^2+q^2}\right)^2 & +\left(\sqrt{(p-1)^2+q^2}\right)^2 \\ & =p^2+2 p+1+q^2+p^2-2 p+1+q^2 \\ & =2 p^2+2+2 q^2=2+2\left(p^2+q^2\right) \\ & =2+2(1)=4 \end{aligned}
2.2 Right Triangle Trigonometry
Homework 2.2.
a \(4\sqrt{13} \approx 14.42\)
b \(\sin \theta = 0.5547, \cos \theta = 0.8321, \tan \theta = 0.6667
a \(4\sqrt{15} \approx 15.49\)
b \(\sin \theta = 0.9682, \cos \theta = 0.2500, \tan \theta = 3.8730\)
a \(2\sqrt{67} \approx 15.49\)
b \(\sin \theta = 0.2116, \cos \theta = 0.9774, \tan \theta = 0.2165\)
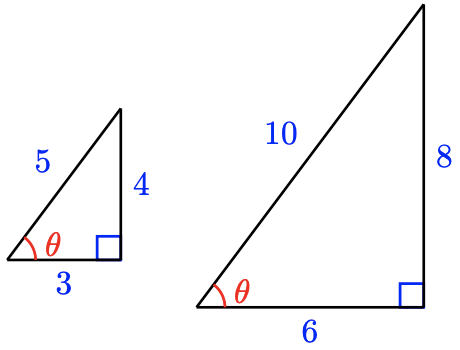
(Answers may vary)
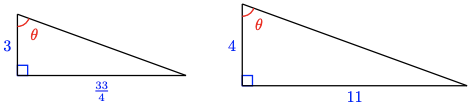
b \(\tan 54.8^{\circ} = \dfrac{h}{20}, 170.1\) yd
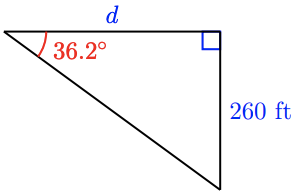
b \(\tan 36.2^{\circ} = \dfrac{260}{d}, 355.2\) ft
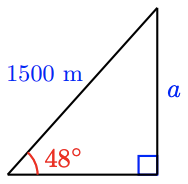
b \(\sin 48^{\circ} = \dfrac{a}{1500}, 1114.7\)m
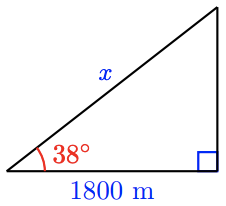
b \(\cos 38^{\circ} = \dfrac{1800}{x}, 2284.2\)m
35. \(x = \dfrac{82}{\tan \theta}\)
37. \(x = 11 \sin \theta\)
39. \(x = \dfrac{9}{\cos \theta}\)
41. \(36 \sin 25^{\circ} \approx 15.21\)
43. \(46 \sin 20^{\circ} \approx 15.73\)
45. \(12 \sin 40^{\circ} \approx 7.71\)
a \(\theta\) and \(\phi\) are complements.
b \(\sin \theta=\cos \phi\) and \(\cos \theta=\sin \phi\). The side opposite \(\theta\) is the side adjacent to \(\phi\), and vice versa.
a As \(\theta\) increases, \(\tan \theta\) increases also. The side opposite \(\theta\) increases in length while the side adjacent to \(\theta\) remains fixed.
b As \(\theta\) increases, \(\cos \theta\) decreases. The side adjacent to \(\theta\) remains fixed while the hypotenuse increases in length.
55. As \(\theta\) decreases toward \(0^{\circ}\), the side opposite \(\theta\) approaches a length of 0, so \(\sin \theta\) approaches 0. But as \(\theta\) increases toward \(90^{\circ}\), the length of the side opposite \(\theta\) approaches the length of the hypotenuse, so \(\sin \theta\) approaches 1.
57. The triangle is not a right triangle.
59. \(\dfrac{21}{20}\) is the ratio of hypotenuse to the adjacent side, which is the reciprocal of \(\cos \theta\).
a \(0.2358\)
c \(48^{\circ}\)
d \(77^{\circ}\)
a \(\dfrac{5}{12}\)
c \(\dfrac{2}{3}\)
d \(\dfrac{2}{\sqrt{7}}\)
65. Although the triangles may differ in size, the ratio of the side adjacent to the angle to the hypotenuse of the triangle remains the same because the triangles would all be similar, and hence corresponding sides are proportional.
a \(\dfrac{2}{3}\)
b \(\dfrac{2}{3}\)
2.3 Solving Right Triangles
Homework 2.3.
1. \(A = 61^{\circ}, a = 25.26, c = 28.88\)
3. \(A = 68^{\circ}, a = 0.93, b = 0.37\)
b \(B = 48^{\circ}, a = 17.4, b = 19.3\)
b \(A=57^{\circ}, b=194.4, c=357.7\)
b \(B=78^{\circ}, b=18.8, c=19.2\)
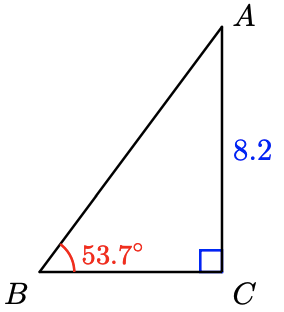
- Solve \(\sin 53.7^{\circ} = \dfrac{8.2}{c}\) for \(c\).
- Solve \(\tan 53.7^{\circ} = \dfrac{8.2}{a}\) for \(a\).
- Subtract \(53.7^{\circ}\) from \(90^{\circ}\) to find \(A\).
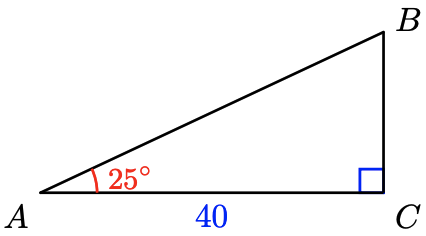
- Solve \(\cos 25^{\circ} = \dfrac{40}{c}\) for \(c\).
- Solve \(\tan 25^{\circ} = \dfrac{a}{40}\) for \(a\).
- Subtract \(25^{\circ}\) from \(90^{\circ}\) to find \(B\).
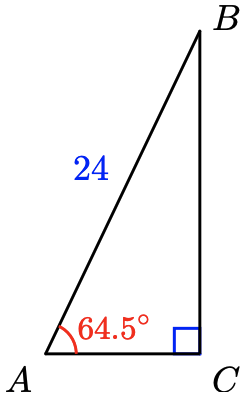
- Solve \(\sin 64.5^{\circ} = \dfrac{a}{24}\) for \(a\).
- Solve \(\cos 64.5^{\circ} = \dfrac{b}{24}\) for \(b\).
- Subtract \(64.5^{\circ}\) from \(90^{\circ}\) to find \(B\).
17. \(74.2^{\circ}\)
19. \(56.4^{\circ}\)
21. \(66.0^{\circ}\)
23. \(11.5^{\circ}\)
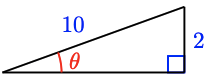
25. \(56.3^{\circ}\)
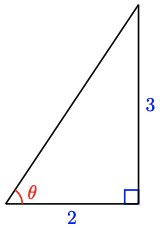
27. \(73.5^{\circ}\)
29. \(\cos 15^{\circ} = 0.9659\) and \(\cos ^{-1} 0.9659 = 15^{\circ}\)
31. \(\tan 65^{\circ} = 2.1445\) and \(\tan ^{-1} 2.1445 = 65^{\circ}\)
33. \(\sin ^{-1} (0.6) \approx 36.87^{\circ}\) is the angle whose sine is 0.6. \((\sin 6^{\circ})^{-1} \approx 9.5668\) is the reciprocal of \(\sin 6^{\circ}\).

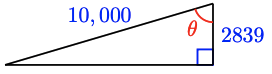
b \(\sin \theta = \dfrac{1806}{3(2458)}, 14.6^{\circ}\)
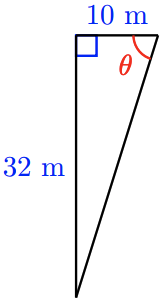
b \(\tan \theta=\dfrac{32}{10}, 72.6^{\circ}\)
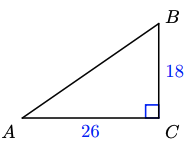
b \(c=10 \sqrt{10} \approx 31.6, A \approx 34.7^{\circ}, B \approx 55.3^{\circ}\)
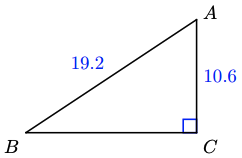
b \(a=\sqrt{256.28} \approx 16.0, A \approx 56.5^{\circ}, B \approx 33.5^{\circ}\)
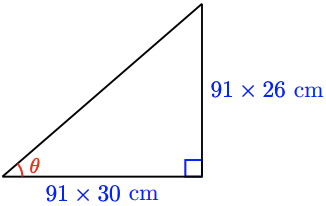
b \(\tan ^{-1}\left(\dfrac{26}{30}\right) \approx 40.9^{\circ}, \quad 91 \sqrt{1676} \approx 3612.6 \mathrm{~cm}\)
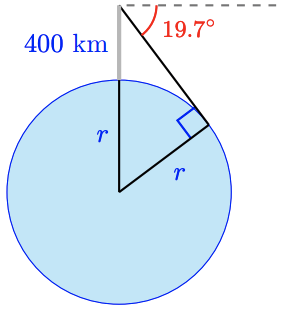
49. (a) and (b)
51. (a) and (d)
53. \(\dfrac{\sqrt{3}}{2} \approx 0.8660\)
55. \(\dfrac{1}{\sqrt{3}} = \dfrac{\sqrt{3}}{3} \approx 0.5774\)
63. \(a=3 \sqrt{3}, b=3, B=30^{\circ}\)
65. \(a=b=4 \sqrt{2}, B=45^{\circ}\)
67. \(e=4, f=4 \sqrt{3}, F=120^{\circ}\)
69. \(d=2 \sqrt{3}, e=2 \sqrt{2}, f=\sqrt{2}+\sqrt{6}, F=75^{\circ}\)
71. \(\a=20, b=20, c=20 \sqrt{2})
a \(32 \sqrt{3} \mathrm{~cm}\)
b \(128 \sqrt{3} \mathrm{sq} \mathrm{cm}\)
a \(10 \mathrm{sq} \mathrm{cm}\)
b \(10 \sqrt{2} \mathrm{sq} \mathrm{cm}\)
c \(10 \sqrt{3} \mathrm{sq} \mathrm{cm}\)
2.4 Chapter 2 Summary and Review
Chapter 2 review problems.
1. If \(C>93^{\circ}\), then \(A+B+C>180^{\circ}\)
3. If \(A<B<58^{\circ}\), then \(A+B+C<180^{\circ}\)
5. If \(C>50^{\circ}\), then \(A+B+C>180^{\circ}\)
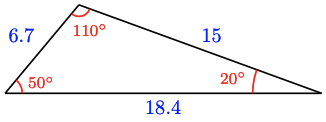
9. \(a = 97\)
11. \(c = 52\)
15. \(\theta=35.26^{\circ}\)
17. No. \(a=6, c=10\) or \(a=9, c=15\)
a \(w=86.05\)
b \(\sin \theta=0.7786, \quad \cos \theta=0.6275, \quad \tan \theta=1.2407\)
a \(y=16.52\)
b \(\sin \theta=0.6957, \quad \cos \theta=0.7184, \quad \tan \theta=0.9684\)
23. \(a = 7.89\)
25. \(x = 3.57\)
27. \(b = 156.95\)
29. \(A=30^{\circ}, a=\dfrac{23 \sqrt{3}}{3}, c=\dfrac{46 \sqrt{3}}{3}\)
31. \(F=105^{\circ}, d=10 \sqrt{2}, e=20, f=10+10 \sqrt{3}\)
35. 43.30 cm
37. 15.92 m
39. \(114.02 \mathrm{ft}, 37.87^{\circ}\)
a \(60.26^{\circ}\)
b \(60.26^{\circ}\)
c \(m=\dfrac{7}{4}=\tan \theta\)
b \(b-a,(b-a)^2\)
c \(\dfrac{1}{2} a b\)
d \(4\left(\dfrac{1}{2} a b\right)+(a-b)^2=2 a b+b^2-2 a b+a^2=a^2+b^2\)
If you're seeing this message, it means we're having trouble loading external resources on our website.
If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.
To log in and use all the features of Khan Academy, please enable JavaScript in your browser.
Trigonometry
Unit 1: right triangles & trigonometry, unit 2: trigonometric functions, unit 3: non-right triangles & trigonometry, unit 4: trigonometric equations and identities, review articles.
Working with Trigonometric Ratios
6.1: This Time with Strategies (5 minutes)
CCSS Standards
- HSG-SRT.C.6
This warm-up uses a problem students didn’t know how to approach at the beginning of the unit. At this point they can try again using the right triangle table. Then when students learn to look up trigonometric ratios in the calculator, that procedure will be solidly grounded in conceptual understanding.
Student Facing
Estimate the value of \(z\) .

Student Response
For access, consult one of our IM Certified Partners .
Activity Synthesis
Point out to students this is the triangle they didn’t know how to approach at the beginning of the unit. Now they have a strategy for finding side lengths of right triangles for acute angles included in the right triangle table. The purpose of this lesson is to teach a method that works for any angle, not just the ones in the table.
6.2: New Names, Same Ratios (15 minutes)
Routines and Materials
Instructional Routines
- MLR8: Discussion Supports
The purpose of this activity is to connect the work students have done in previous lessons and the warm-up to trigonometric ratios. Students learn the names of the trigonometric ratios and how to look them up in the calculator. To continue solidifying their conceptual understanding, students compare the calculator’s value to their work with the right triangle table.
Tell students, “The right triangle table is useful, but what if the angle is not a multiple of 10 degrees? There must be a way to move from estimating to calculating. The name of the column in the right triangle table, 'adjacent leg divided by the hypotenuse,' is long, so mathematicians call this ratio cosine . The column called 'opposite leg divided by the hypotenuse' is named sine . The column called 'opposite leg divided by the adjacent leg' is named tangent . These three names describe trigonometric ratios . Label the columns of the right triangle table with the corresponding trigonometric function names.”
“The word trigonometric comes from the ancient roots of trigon (think about what pentagon or hexagon mean) and metric (like measure). So the word trigonometric comes from ancient words meaning triangle measurement.”
“Cosine, sine, and tangent work like functions where the input is the measure of an angle and the output is a ratio. Scientific calculators can display the ratio for any angle, even ones not included in the table. First, identify that we have an angle measure and the length of the adjacent leg. Then identify that we are looking for the length of the hypotenuse. The ratio of adjacent leg divided by hypotenuse is called cosine. So we can write \(\cos(50)=\frac{3}{z}\) .” Demonstrate how to use the technology available to solve this type of problem. Typing \(\cos(50)\) into the calculator and then substituting gives the new equation \(0.643=\frac{3}{z}\) . (Note: if students don’t get 0.643, check the mode of the calculator. There is no need to discuss the meaning of radians now, but students will see radians later in this course.)
- Use your calculator to determine the values of \(\cos(50)\) , \(\sin(50)\) , and \(\tan(50)\) .
- Use your calculator to determine the values of \(\cos(40)\) , \(\sin(40)\) , and \(\tan(40)\) .
- How do these values compare to your chart?
- Find the value of \(z\) .
Invite students to share their new value for \(z\) . (Solving the equation we wrote in the launch gives \(z=4.7\) units.)
Ask students:
- “How does this answer compare to using the table?” (It’s the same.)
- “Which one is more trustworthy?” (All opinions are valid.)
- “Which one is more accurate?” (The calculator is much more accurate than the table for numbers between decade numbers. The calculator gives more decimal places, and it’s possible to solve without rounding to get a more precise answer.)
Inform students it is also okay to leave answers in the form \(z=\frac{3}{\cos(50)}\) which would be exact.
Ask students to add these definitions to their reference charts as you add them to the class reference chart:
The cosine of an acute angle in a right triangle is the ratio (quotient) of the length of the adjacent leg to the length of the hypotenuse.
\(\cos(\theta)=\frac{\text{adjacent}}{\text{hypotenuse}}\)
The sine of an acute angle in a right triangle is the ratio (quotient) of the length of the opposite leg to the length of the hypotenuse.
\(\sin(\theta)=\frac{\text{opposite}}{\text{hypotenuse}}\)
The tangent of an acute angle in a right triangle is the ratio (quotient) of the length of the opposite leg to the length of the adjacent leg.
\(\tan(\theta)=\frac{\text{opposite}}{\text{adjacent}}\)
6.3: Solve These Triangles (15 minutes)
Building On
- Think Pair Share
Required Materials
- Scientific calculators
Students apply their new knowledge of trigonometric ratios to solve these problems. Since these problems ask for multiple side and angle measures, there is an increased opportunity for creativity in solving.
Monitor for students who solve multiple trigonometric equations versus those that apply the Pythagorean Theorem.
Arrange students in groups of 2. Ask students to compare their strategy with their partner’s and decide if they are both correct, even if they are different.
Students need not complete all the problems before the discussion.
Solve for \(x\) .
Solve for \(y\) .
Find all the missing sides and angle measures.
The measure of angle \(X\) is 90 degrees and angle \(Y\) is 12 degrees. Side \(XZ\) has length 2 cm.
The measure of angle \(K\) is 90 degrees and angle \(L\) is 71 degrees. Side \(LM\) has length 20 cm.
Are you ready for more?
Complete the table.
Based on this information, what do you think are the cosine, sine, and tangent of 90 degrees? Explain or show your reasoning.
Anticipated Misconceptions
If students struggle to get started, prompt them to set up ratios to find the missing sides. If students struggle to set up ratios, prompt them to identify what is known and what they are looking to find by annotating the diagram.
Invite students to contrast solving multiple trigonometric equations versus applying the Pythagorean Theorem to determine the final side length. Is one method easier? More accurate? (The Pythagorean Theorem is more familiar so I prefer it. Both methods are accurate so long as you don't round too much.)
Call attention to the triangle with no marked right angle. Ask students, “How do you know you can use trigonometric functions with this triangle?” (By the Triangle Angle Sum Theorem the third angle must be 90 degrees.)
Lesson Synthesis
Display this triangle and give students quiet work time to write as many equations as they can to show the relationships in triangle \(END\) .
Invite students to share one equation at a time until you have recorded two of each trigonometric ratio ( cosine, sine, and tangent ):
\(\cos(35)=\frac{d}{n}\)
\(\sin(35)=\frac{e}{n}\)
\(\tan(35)=\frac{e}{d}\)
\(\cos(55)=\frac{e}{n}\)
\(\sin(55)=\frac{d}{n}\)
\(\tan(55)=\frac{d}{e}\)
Tell students the value of \(d\) is 6 units. First, ask them to consider which equations would be helpful in solving for the other sides. Then give them time to do the calculations ( \(e=4.2 \) units, \(n=7.3\) units). If students get slightly different answers, take the opportunity to discuss precision and rounding error.
6.4: Cool-down - Solve That Triangle (5 minutes)
Student lesson summary.
We have a column in the right triangle table for "adjacent leg \(\div\) hypotenuse." We use this ratio so frequently it has a name. It is called the cosine of the angle. We write \(\cos(25)\) to say the cosine of 25 degrees. A scientific calculator can display the cosine of any angle. This means we can more precisely calculate unknown side lengths rather than estimating using the table. The right triangle table is sometimes called a trigonometry table since cosine, sine , and tangent are trigonometric ratios . Here is what the table looks like with the ratios labeled with their special names:
If the length \(b\) is 7, we can find \(c\) by solving the equation \(\cos(25)=\frac{7}{c}\) . So \(c\) is about 7.7 units. To solve for \(a\) we have 3 choices: the Pythagorean Theorem, sine, and tangent. Let’s use tangent by solving the equation \(\tan(25)=\frac{a}{7}\) . So \(a\) is about 3.3 units. We can check our answers using the Pythagorean Theorem. It should be true that \(3.3^2+7^2=7.7^2\) . The two expressions are almost equal, which makes sense because we expect some error due to rounding.
Chapter 10, Lesson 8: Trigonometric Ratios
- Extra Examples
- Personal Tutor
- Self-Check Quizzes
The resource you requested requires you to enter a username and password below:
Please read our Terms of Use and Privacy Notice before you explore our Web site. To report a technical problem with this Web site, please contact the site producer .


IMAGES
VIDEO
COMMENTS
Sin, cos, and tan are trigonometric ratios that relate the angles and sides of right triangles. Sin is the ratio of the opposite side to the hypotenuse, cos is the ratio of the adjacent side to the hypotenuse, and tan is the ratio of the opposite side to the adjacent side. They are often written as sin (x), cos (x), and tan (x), where x is an ...
Learn for free about math, art, computer programming, economics, physics, chemistry, biology, medicine, finance, history, and more. ... Report a problem. Stuck? Review related articles/videos or use a hint. ... Introduction to the trigonometric ratios. Triangle similarity & the trigonometric ratios.
G.SRT.C.8 — Use trigonometric ratios and the Pythagorean Theorem to solve right triangles in applied problems. Modeling is best interpreted not as a collection of isolated topics but in relation to other standards. Making mathematical models is a Standard for Mathematical Practice, and specific modeling standards appear throughout the high school standards indicated by a star symbol (★).
10-1 Trigonometric Ratios. Use the figure for Exercises 1-6. Write each trigonometric ratio as a simplified fraction and as a decimal rounded to the nearest hundredth. Use special right triangles to write each trigonometric ratio as a simplified fraction. Use a calculator to find each trigonometric ratio.
Solution to Problem 1: First we need to find the hypotenuse using Pythagora's theorem. (hypotenuse) 2 = 8 2 + 6 2 = 100. and hypotenuse = 10. We now use the definitions of the six trigonometric ratios given above to find sin A, cos A, tan A, sec A, csc A and cot A. sin A = side opposite angle A / hypotenuse = 8 / 10 = 4 / 5.
Vector Spaces: In linear algebra and vector calculus, trigonometric functions can be used to describe the relationships between vectors in higher-dimensional spaces. For example, the dot product between two vectors involves the cosine of the angle between them, and this concept extends to higher dimensions.
Example: Use the calculator to find an angle θ in the interval [0, 90] that satisfies the equation. sin θ = 0.7523. tan θ = 3.54. Solve the given right triangle if a = 44.3 cm and b = 55.9 cm. Find each angle in a 3,4,5 triangle. Show Video Lesson.
Lesson Worksheet. This lesson plan includes the objectives, prerequisites, and exclusions of the lesson teaching students how to find and express the values of the three trigonometric ratios—sine, cosine, and tangent—for a given angle in a right triangle.
Learn what trigonometric ratios are, learn how to solve for sides and angles, and practice finding these trigonometric ratios in a practice problem. Create an account Table of Contents
It is the ratio of the side lengths, so the Opposite is about 0.7071 times as long as the Hypotenuse. We can now put 0.7071... in place of sin(45°): ... Solving Triangles. Trigonometry is also useful for general triangles, not just right-angled ones . It helps us in Solving Triangles. "Solving" means finding missing sides and angles.
1 Use measurements to calculate the trigonometric ratios for acute angles #1-10, 57-60. 2 Use trigonometric ratios to find unknown sides of right triangles #11-26. 3 Solve problems using trigonometric ratios #27-34, 41-46. 4 Use trig ratios to write equations relating the sides of a right triangle #35-40. 5 Use relationships among the ...
Determine the six trigonometric ratios for angle A in the right triangle. In this tutorial you are shown how to name the sides of any right-angled triangle which is the first stage in solving a question in trigonometry. In this tutorial you are shown how the sin, cos and tan ratios compare two sides of a right-angled triangle.
8.2: The Trigonometric Ratios. There are six common trigonometric ratios that relate the sides of a right triangle to the angles within the triangle. The three standard ratios are the sine, cosine and tangent. These are often abbreviated sin, cos and tan.
Some trigonometric solutions based problems on trigonometric ratios are shown here with the step-by-step explanation. 1. If sin θ = 8/17, find other trigonometric ratios of <θ. ... We will solve the different types of problems involving addition and subtraction together. To show the problem involving both addition and subtraction, we first ...
Read the problem and make sure all the words and ideas are understood. Draw the right triangle and label the given parts. Identify what we are looking for.; Label what we are looking for by choosing a variable to represent it.; Find the required trigonometric ratio.; Solve the ratio using good algebra techniques.; Check the answer by substituting it back into the ratio in step 4 and by making ...
This page titled 11.1: The Trigonometric Ratios is shared under a GNU Free Documentation License 1.3 license and was authored, remixed, and/or curated by Katherine Yoshiwara via source content that was edited to the style and standards of the LibreTexts platform; a detailed edit history is available upon request.
Lesson Plan Launch (10 min) Students: Sketch real world problems of triangles and angles. Also define depression/ elevation ... (7 min) Go through steps to solve a word problems using trig ratios Go through each step with the example, completing steps as we go through the example (8 min): Example #2 - read step 1 then have a student's ...
Trigonometry 4 units · 36 skills. Unit 1 Right triangles & trigonometry. Unit 2 Trigonometric functions. Unit 3 Non-right triangles & trigonometry. Unit 4 Trigonometric equations and identities. Course challenge. Test your knowledge of the skills in this course. Start Course challenge. Math.
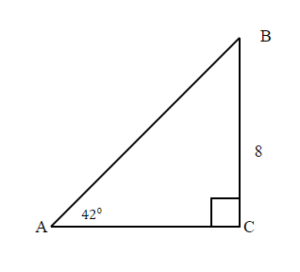
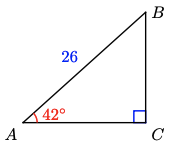
Lesson 12.1 • Trigonometric Ratios (continued) You can use trigonometric ratios to find unknown side lengths of a right triangle given the measures of any side and any acute angle. Read Example B in your book and then read Example A below. EXAMPLE A Find the value ofx. Solution You need to find the length of the side adjacent to the 42 ...
The purpose of this lesson is to teach a method that works for any angle, not just the ones in the table. 6.2: New Names, Same Ratios (15 minutes) CCSS Standards. ... Students apply their new knowledge of trigonometric ratios to solve these problems. Since these problems ask for multiple side and angle measures, there is an increased ...
Log In. The resource you requested requires you to enter a username and password below: