statistics chapter 8 homework

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons
• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

15.2.7: Chapter 8 Homework

• Last updated
• Save as PDF
• Page ID 28310

• Maurice A. Geraghty
• De Anza College
• State in your own words the 3 important parts of the Central Limit Theorem.
• Find the probability that a woman aged 18‐24 has systolic blood pressure exceeding 120.
• If 4 women are randomly selected, find the probability that their mean blood pressure exceeds 120.  
• If 40 women are randomly selected, find the probability that their mean blood pressure exceeds 120.  
• If the pdf for systolic blood pressure did NOT follow a normal distribution, would your answer to part c change? Explain.
• If you sample 1 package, find the probability that the sample mean is over 66 g.  
• If you sample 16 packages, find the probability that the sample mean is over 66 g. Compare this answer to part a.
• If you sample 49 packages, find the probability that the sample mean is over 66 g. Compare this answer to parts a and b.
• In a sample of 16 Americans, what is the probability that the sample mean will exceed 57 pounds of HFCS per year?
• In a sample of 16 Americans, what is the probability that the sample mean will be between 50 and 70 pounds of HFCS per year.
• In a sample of 16 Americans, between what two values would you expect to see 95% of the sample means?
• The completion time (in minutes) for a student to complete a short quiz follows the continuous probability density function shown here, with some areas calculated. It is known that \(\mu=5.3\) minutes and \(\sigma=2.4\) minutes. 40 students take the quiz.

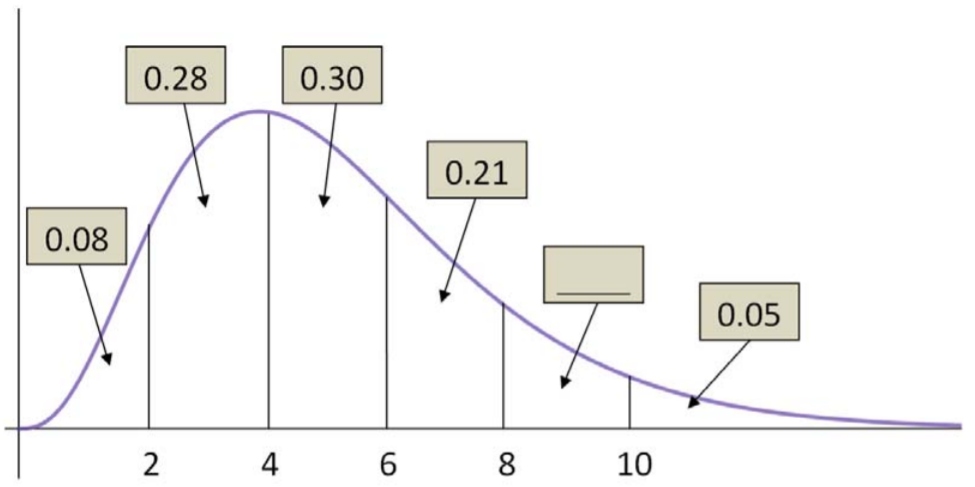
• Find the mean completion time for the students is under 5 minutes.
• Find the probability that the mean time for the class to finish the quiz is between  6 and 8 minutes.
• The mean completion time for the class was 7.1 minutes. Is this result unusual? Explain.
• 61% of Californians live in Southern California.
• 92% of Californians support Deferred Action for Childhood Arrivals (DACA).
• 24% of Californians have visited Yosemite National Park.
• 8% of Californians have a felony conviction.
• Find the mean and standard deviation for cycle times.
• There have been 46 times that concrete has been hauled to the construction site. Find the probability that the mean cycle time for these 46 samples exceeds 58 minutes.
• What is the mean and standard deviation of the random variable X?
• For 35 accidents at nuclear power plants, the mean waiting time was 6.1 years. Is this value unusually low? To answer, find the probability that the mean waiting time is 6.1 years or less.

Introduction

Chapter objectives.

By the end of this chapter, the student should be able to:

• Calculate and interpret confidence intervals for estimating a population mean and a population proportion.
• Interpret the Student's t probability distribution as the sample size changes.
• Discriminate between problems applying the normal and the Student's t distributions.
• Calculate the sample size required to estimate a population mean and a population proportion given a desired confidence level and margin of error.

Suppose you were trying to determine the mean rent of a two-bedroom apartment in your town. You might look in the classified section of the newspaper, write down several rents listed, and average them together. You would have obtained a point estimate of the true mean. If you are trying to determine the percentage of times you make a basket when shooting a basketball, you might count the number of shots you make and divide that by the number of shots you attempted. In this case, you would have obtained a point estimate for the true proportion.

We use sample data to make generalizations about an unknown population. This part of statistics is called inferential statistics . The sample data help us to make an estimate of a population parameter . We realize that the point estimate is most likely not the exact value of the population parameter, but close to it. After calculating point estimates, we construct interval estimates, called confidence intervals.

In this chapter, you will learn to construct and interpret confidence intervals. You will also learn a new distribution, the Student's-t, and how it is used with these intervals. Throughout the chapter, it is important to keep in mind that the confidence interval is a random variable. It is the population parameter that is fixed.

If you worked in the marketing department of an entertainment company, you might be interested in the mean number of songs a consumer downloads a month from Apple Music. If so, you could conduct a survey and calculate the sample mean, x ¯ x ¯ , and the sample standard deviation, s . You would use x ¯ x ¯ to estimate the population mean and s to estimate the population standard deviation. The sample mean, x ¯ x ¯ , is the point estimate for the population mean, μ . The sample standard deviation, s , is the point estimate for the population standard deviation, σ .

Each of x ¯ x ¯ and s is called a statistic.

A confidence interval is another type of estimate but, instead of being just one number, it is an interval of numbers. It provides a range of reasonable values in which we expect the population parameter to fall. There is no guarantee that a given confidence interval does capture the parameter, but there is a predictable probability of success.

Suppose, for the Apple Music example, we do not know the population mean μ , but we do know that the population standard deviation is σ = 1 and our sample size is 100. Then, by the central limit theorem, the standard deviation for the sample mean is

The Empirical Rule , which applies to bell-shaped distributions, says that in approximately 95% of the samples, the sample mean, x ¯ x ¯ , will be within two standard deviations of the population mean μ . For our Apple Music example, two standard deviations is (2)(0.1) = 0.2. The sample mean x ¯ x ¯ is likely to be within 0.2 units of μ .

Because x ¯ x ¯ is within 0.2 units of μ , which is unknown, then μ is likely to be within 0.2 units of x ¯ x ¯ in 95% of the samples. The population mean μ is contained in an interval whose lower number is calculated by taking the sample mean and subtracting two standard deviations (2)(0.1) and whose upper number is calculated by taking the sample mean and adding two standard deviations. In other words, μ is between x ¯   −  0 .2 x ¯   −  0 .2 and x ¯   +  0 .2 x ¯   +  0 .2 in 95% of all the samples.

For the Apple Music example, suppose that a sample produced a sample mean x ¯   =  2 x ¯   =  2 . Then the unknown population mean μ is between

x ¯ − 0.2 = 2 − 0.2 = 1.8 x ¯ − 0.2 = 2 − 0.2 = 1.8 and x ¯ + 0.2 = 2 + 0.2 = 2.2 x ¯ + 0.2 = 2 + 0.2 = 2.2

We say that we are 95% confident that the unknown population mean number of songs downloaded from Apple Music per month is between 1.8 and 2.2. The 95% confidence interval is (1.8, 2.2).

The 95% confidence interval implies two possibilities. Either the interval (1.8, 2.2) contains the true mean μ or our sample produced an x ¯ x ¯ that is not within 0.2 units of the true mean μ . The first possibility happens for 95% of well-chosen samples. It is important to remember that the second possibility happens for 5% of samples, even though correct procedures are followed.

Remember that a confidence interval is created for an unknown population parameter like the population mean, μ . Confidence intervals for some parameters have the form:

(point estimate – margin of error, point estimate + margin of error )

The margin of error depends on the confidence level or percentage of confidence and the standard error of the mean.

When you read newspapers and journals, some reports will use the phrase "margin of error." Other reports will not use that phrase, but include a confidence interval as the point estimate plus or minus the margin of error. These are two ways of expressing the same concept.

Although the text only covers symmetrical confidence intervals, there are non-symmetrical confidence intervals (for example, a confidence interval for the standard deviation).

Collaborative Exercise

Have your instructor record the number of meals each student in your class eats out in a week. Assume that the standard deviation is known to be three meals. Construct an approximate 95% confidence interval for the true mean number of meals students eat out each week.

• Calculate the sample mean.
• Let σ = 3 and n = the number of students surveyed.
• Construct the interval ( x ¯ − 2 ⋅ σ n ,  x ¯  +  2 ⋅ σ n ) ( x ¯ − 2 ⋅ σ n ,  x ¯  +  2 ⋅ σ n ) .

We say we are approximately 95% confident that the true mean number of meals that students eat out in a week is between __________ and ___________.

This book may not be used in the training of large language models or otherwise be ingested into large language models or generative AI offerings without OpenStax's permission.

Want to cite, share, or modify this book? This book uses the Creative Commons Attribution License and you must attribute OpenStax.

Access for free at https://openstax.org/books/introductory-statistics-2e/pages/1-introduction

• Authors: Barbara Illowsky, Susan Dean
• Publisher/website: OpenStax
• Book title: Introductory Statistics 2e
• Publication date: Dec 13, 2023
• Location: Houston, Texas
• Book URL: https://openstax.org/books/introductory-statistics-2e/pages/1-introduction
• Section URL: https://openstax.org/books/introductory-statistics-2e/pages/8-introduction

© Dec 6, 2023 OpenStax. Textbook content produced by OpenStax is licensed under a Creative Commons Attribution License . The OpenStax name, OpenStax logo, OpenStax book covers, OpenStax CNX name, and OpenStax CNX logo are not subject to the Creative Commons license and may not be reproduced without the prior and express written consent of Rice University.

Chapter 6: The Normal Distribution and The Central Limit Theorem

6.1 The Standard Normal Distribution

Learning objectives.

By the end of this section, the student should be able to:

• Calculate and interpret z-scores.
• Recognize characteristics of the standard normal distribution.
• Apply the empirical rule to solve real-world applications.

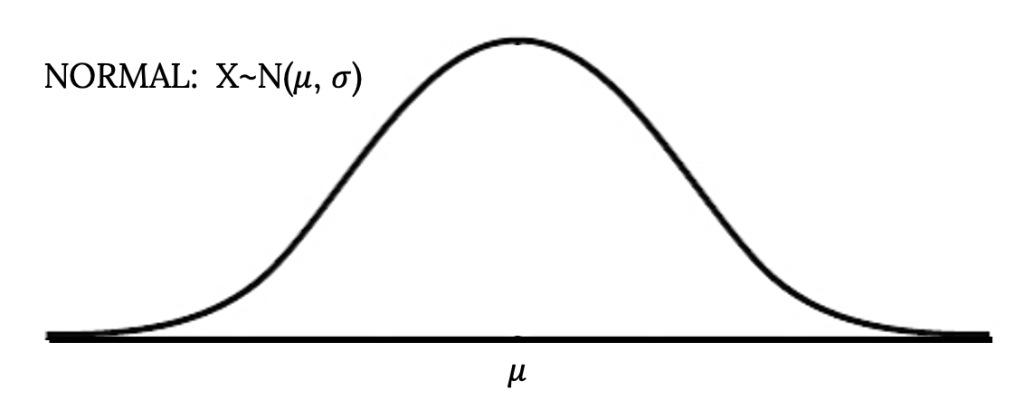
The normal distribution has two parameters (two numerical descriptive measures): the mean ( μ ) and the standard deviation ( σ ). If X is a quantity to be measured that has a normal distribution with mean ( μ ) and standard deviation ( σ ), we designate this by writing X~N(μ, σ).

The probability density function of this curve is as follows:

f ( x ) = [latex]\frac{1}{\sigma \cdot \sqrt{2\cdot \pi }} \cdot {\text{ e}}^{-\frac{1}{2}\cdot {\left(\frac{x-\mu }{\sigma }\right)}^{2}}[/latex]

• -∞ < X < ∞
• -∞ < μ < ∞

As you can see, the normal pdf is a rather complicated function. Do not memorize it . It is not necessary. But this could be a problem since the normal distribution is so widely used. However we will see some ways we can work around this.

The cumulative distribution function is P ( X < x ). It is calculated either by a calculator or a computer, or it is looked up in a table. Technology has made the tables virtually obsolete.

The curve is symmetrical about a vertical line drawn through the mean, μ . In theory, the mean is the same as the median, because the graph is symmetric about μ . As the notation indicates, the normal distribution depends only on the mean and the standard deviation. Since the area under the curve must equal one, a change in the standard deviation, σ , causes a change in the shape of the curve; the curve becomes fatter or skinnier depending on σ . A change in μ causes the graph to shift to the left or right. This means there are an infinite number of normal probability distributions. One of special interest is called the standard normal distribution .

The standard normal distribution is a normal distribution of standardized values called z -scores . A z -score is measured in units of the standard deviation. For example, if the mean of a normal distribution is five and the standard deviation is two, the value 11 is three standard deviations above (or to the right of) the mean. The calculation is as follows:

x = μ + ( z )( σ ) = 5 + (3)(2) = 11

The z -score is three.

The mean for the standard normal distribution is zero, and the standard deviation is one. The transformation z = [latex]\frac{x-\mu }{\sigma }[/latex] produces the distribution Z ~ N (0, 1). The value x comes from a normal distribution with mean μ and standard deviation σ .

If X is a normally distributed random variable and X ~ N(μ, σ) , then the z -score is:

The z -score tells you how many standard deviations the value x is above (to the right of) or below (to the left of) the mean, μ . Values of x that are larger than the mean have positive z -scores, and values of x that are smaller than the mean have negative z -scores. If x equals the mean, then x has a z -score of zero.

Suppose X ~ N(5, 6) . This says that x is a normally distributed random variable with mean μ = 5 and standard deviation σ = 6. Suppose x = 17.

Then: [latex]z=\frac{x–\mu }{\sigma }=\frac{17–5}{6}=2[/latex]

This means that x = 17 is two standard deviations (2 σ ) above or to the right of the mean μ = 5. The standard deviation is σ = 6.

Notice that: 5 + (2)(6) = 17 (The pattern is μ + zσ = x )

Now suppose x = 1. Then: z = [latex]\frac{x–\mu }{\sigma }[/latex] = [latex]\frac{1–5}{6}[/latex] = –0.67 (rounded to two decimal places)

This means that x = 1 is 0.67 standard deviations (–0.67 σ ) below or to the left of the mean μ = 5. Notice that: 5 + (–0.67)(6) is approximately equal to one (This has the pattern μ + (–0.67)σ = 1)

Summarizing, when z is positive, x is above or to the right of μ and when z is negative, x is to the left of or below μ . Or, when z is positive, x is greater than μ , and when z is negative x is less than μ .

Some doctors believe that a person can lose five pounds, on the average, in a month by reducing his or her fat intake and by exercising consistently. Suppose weight loss has a normal distribution. Let X = the amount of weight lost(in pounds) by a person in a month. Use a standard deviation of two pounds. X ~ N (5, 2). Fill in the blanks.

a. Suppose a person lost ten pounds in a month. The z -score when x = 10 pounds is z = 2.5 (verify). This z -score tells you that x = 10 is ________ standard deviations to the ________ (right or left) of the mean _____ (What is the mean?).

This z -score tells you that x = 10 is 2.5 standard deviations to the right of the mean five .

b. Suppose a person gained three pounds (a negative weight loss). Then z = __________. This z -score tells you that x = –3 is ________ standard deviations to the __________ (right or left) of the mean.

z = –4 . This z -score tells you that x = –3 is four standard deviations to the left of the mean.

c. Suppose the random variables X and Y have the following normal distributions: X ~ N (5, 6) and Y ~ N (2, 1). If x = 17, then z = 2. (This was previously shown.) If y = 4, what is z ?

z = [latex]\frac{y-\mu }{\sigma }[/latex] = [latex]\frac{4-2}{1}[/latex] = 2 where µ = 2 and σ = 1.

The z -score for y = 4 is z = 2. This means that four is z = 2 standard deviations to the right of the mean. Therefore, x = 17 and y = 4 are both two (of their own ) standard deviations to the right of their respective means.

The z -score allows us to compare data that are scaled differently. To understand the concept, suppose X ~ N (5, 6) represents weight gains for one group of people who are trying to gain weight in a six week period and Y ~ N (2, 1) measures the same weight gain for a second group of people. A negative weight gain would be a weight loss. Since x = 17 and y = 4 are each two standard deviations to the right of their means, they represent the same, standardized weight gain relative to their means .

What is the z -score of x , when x = 1 and X ~ N (12,3)?

[latex]z=\frac{1–12}{3}\approx –3.67[/latex]

The mean height of 15 to 18-year-old males from Chile from 2009 to 2010 was 170 cm with a standard deviation of 6.28 cm. Male heights are known to follow a normal distribution. Let X = the height of a 15 to 18-year-old male from Chile in 2009 to 2010. Then X ~ N (170, 6.28).

a. Suppose a 15 to 18-year-old male from Chile was 168 cm tall from 2009 to 2010. The z -score when x = 168 cm is z = _______. This z -score tells you that x = 168 is ________ standard deviations to the ________ (right or left) of the mean _____ (What is the mean?).

z = –0.32, z = 0.32, left, μ = 170

b. Suppose that the height of a 15 to 18-year-old male from Chile from 2009 to 2010 has a z -score of z = 1.27. What is the male’s height? The z -score ( z = 1.27) tells you that the male’s height is ________ standard deviations to the __________ (right or left) of the mean.

x = 177.98, 1.27, right

1. Suppose a 15 to 18-year-old male from Chile was 176 cm tall from 2009 to 2010. The z -score when x = 176 cm is z = _______. This z -score tells you that x = 176 cm is ________ standard deviations to the ________ (right or left) of the mean _____ (What is the mean?).

2. Suppose that the height of a 15 to 18-year-old male from Chile from 2009 to 2010 has a z -score of z = –2. What is the male’s height? The z -score ( z = –2) tells you that the male’s height is ________ standard deviations to the __________ (right or left) of the mean.

Solve the equation z = [latex]\frac{x-\mu }{\sigma }[/latex] for x . x = μ + ( z )( σ )

• z = [latex]\frac{176-170}{6.28}[/latex] ≈ 0.96, This z -score tells you that x = 176 cm is 0.96 standard deviations to the right of the mean 170 cm.
• X = 157.44 cm, The z -score( z = –2) tells you that the male’s height is two standard deviations to the left of the mean

From 1984 to 1985, the mean height of 15 to 18-year-old males from Chile was 172.36 cm, and the standard deviation was 6.34 cm. Let Y = the height of 15 to 18-year-old males from 1984 to 1985. Then Y ~ N (172.36, 6.34).

Find the z -scores for x = 160.58 cm and y = 162.85 cm. Interpret each z -score. What can you say about x = 160.58 cm and y = 162.85 cm?

The z -score for x = 160.58 is z = –1.5. The z -score for y = 162.85 is z = –1.5. Both x = 160.58 and y = 162.85 deviate the same number of standard deviations from their respective means and in the same direction.

In 2012, 1,664,479 students took the SAT exam. The distribution of scores in the verbal section of the SAT had a mean µ = 496 and a standard deviation σ = 114. Let X = a SAT exam verbal section score in 2012. Then X ~ N (496, 114).

Find the z -scores for x 1 = 325 and x 2 = 366.21. Interpret each z -score. What can you say about x 1 = 325 and x 2 = 366.21?

The z -score for x 1 = 325 is z 1 = –1.14.

The z -score for x 2 = 366.21 is z 2 = –1.14.

Student 2 scored closer to the mean than Student 1 and, since they both had negative z -scores, Student 2 had the better score.

Fill in the blanks.

Jerome averages 16 points a game with a standard deviation of four points. X ~ N (16,4). Suppose Jerome scores ten points in a game. The z –score when x = 10 is –1.5. This score tells you that x = 10 is _____ standard deviations to the ______(right or left) of the mean______(What is the mean?).

1.5, left, 16

The Empirical Rule

The Empirical Rule If X is a random variable and has a normal distribution with mean µ and standard deviation σ , then the Empirical Rule says the following:

• About 68% of the x values lie between –1 σ and +1 σ of the mean µ (within one standard deviation of the mean). The z -scores for +1 σ and –1 σ are +1 and –1, respectively.
• About 95% of the x values lie between –2 σ and +2 σ of the mean µ (within two standard deviations of the mean). The z -scores for +2 σ and –2 σ are +2 and –2, respectively.
• About 99.7% of the x values lie between –3 σ and +3 σ of the mean µ (within three standard deviations of the mean). The z -scores for +3 σ and –3 σ are +3 and –3 respectively.

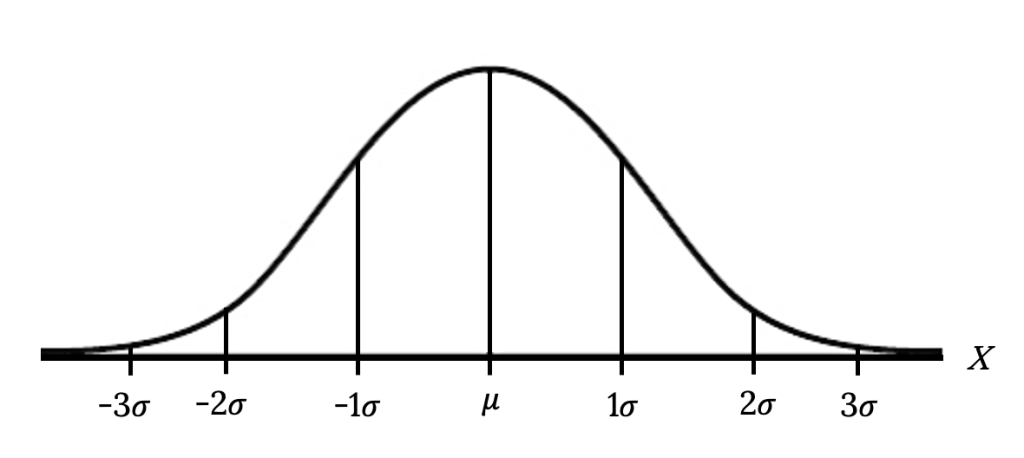
Notice that almost all the x values lie within three standard deviations of the mean. The empirical rule is also known as the 68-95-99.7 rule.

Suppose x has a normal distribution with mean 50 and standard deviation 6.

• About 68% of the x values lie between –1 σ = (–1)(6) = –6 and 1 σ = (1)(6) = 6 of the mean 50. The values 50 – 6 = 44 and 50 + 6 = 56 are within one standard deviation of the mean 50. The z -scores are –1 and +1 for 44 and 56, respectively.
• About 95% of the x values lie between –2 σ = (–2)(6) = –12 and 2 σ = (2)(6) = 12. The values 50 – 12 = 38 and 50 + 12 = 62 are within two standard deviations of the mean 50. The z -scores are –2 and +2 for 38 and 62, respectively.
• About 99.7% of the x values lie between –3 σ = (–3)(6) = –18 and 3 σ = (3)(6) = 18 of the mean 50. The values 50 – 18 = 32 and 50 + 18 = 68 are within three standard deviations of the mean 50. The z -scores are –3 and +3 for 32 and 68, respectively.

From 1984 to 1985, the mean height of 15 to 18-year-old males from Chile was 172.36 cm, and the standard deviation was 6.34 cm. Let Y = the height of 15 to 18-year-old males in 1984 to 1985. Then Y ~ N (172.36, 6.34).

The scores on a college entrance exam have an approximate normal distribution with mean, µ = 52 points and a standard deviation, σ = 11 points.

• About 68% of the y values lie between what two values? These values are ________________. The z -scores are ________________, respectively.
• About 95% of the y values lie between what two values? These values are ________________. The z -scores are ________________, respectively.
• About 99.7% of the y values lie between what two values? These values are ________________. The z -scores are ________________, respectively.
• About 68% of the values lie between the values 41 and 63. The z -scores are –1 and 1, respectively.
• About 95% of the values lie between the values 30 and 74. The z -scores are –2 and 2, respectively.
• About 99.7% of the values lie between the values 19 and 85. The z -scores are –3 and 3, respectively.

Suppose X has a normal distribution with mean 25 and standard deviation five. Between what values of x do 68% of the values lie?

between 20 and 30.

“Blood Pressure of Males and Females.” StatCrunch, 2013. Available online at http://www.statcrunch.com/5.0/viewreport.php?reportid=11960 (accessed May 14, 2013).

“The Use of Epidemiological Tools in Conflict-affected populations: Open-access educational resources for policy-makers: Calculation of z-scores.” London School of Hygiene and Tropical Medicine, 2009. Available online at http://conflict.lshtm.ac.uk/page_125.htm (accessed May 14, 2013).

“2012 College-Bound Seniors Total Group Profile Report.” CollegeBoard, 2012. Available online at http://media.collegeboard.com/digitalServices/pdf/research/TotalGroup-2012.pdf (accessed May 14, 2013).

“Digest of Education Statistics: ACT score average and standard deviations by sex and race/ethnicity and percentage of ACT test takers, by selected composite score ranges and planned fields of study: Selected years, 1995 through 2009.” National Center for Education Statistics. Available online at http://nces.ed.gov/programs/digest/d09/tables/dt09_147.asp (accessed May 14, 2013).

Data from the San Jose Mercury News .

Data from The World Almanac and Book of Facts .

“List of stadiums by capacity.” Wikipedia. Available online at https://en.wikipedia.org/wiki/List_of_stadiums_by_capacity (accessed May 14, 2013).

Data from the National Basketball Association. Available online at www.nba.com (accessed May 14, 2013).

Media Attributions

• Private: Figure 5.10 © Significant Statistics by John Morgan Russell is licensed under a CC BY-SA (Attribution ShareAlike) license
• Private: Figure 5.11 © Significant Statistics by John Morgan Russell is licensed under a CC BY-SA (Attribution ShareAlike) license

A function that defines a continuous random variable, and the likelihood of an outcome

a continuous random variable (RV) with a mean of 0 and a standard deviation of 1 which z-scores follow: X ~ N(0, 1); when X follows the standard normal distribution, it is often noted as Z ~ N(0, 1).

the linear transformation of the form z = [latex]\frac{x\text{ }–\text{ }\mu }{\sigma }[/latex]; if this transformation is applied to any normal distribution X ~ N(μ, σ) the result is the standard normal distribution Z ~ N(0,1). If this transformation is applied to any specific value x of the RV with mean μ and standard deviation σ, the result is called the z-score of x. The z-score allows us to compare data that are normally distributed but scaled differently.

Roughly 68% of values are within 1 standard deviation of the mean, roughly 95% of values are within 2 standard deviations of the mean, and 99.7% of values are within 3 standard deviations of the mean

Introductory Statistics Copyright © 2024 by LOUIS: The Louisiana Library Network is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License , except where otherwise noted.

Share This Book