hypothesis test conclusion

Statistics Made Easy

How to Write Hypothesis Test Conclusions (With Examples)

A   hypothesis test is used to test whether or not some hypothesis about a population parameter is true.

To perform a hypothesis test in the real world, researchers obtain a random sample from the population and perform a hypothesis test on the sample data, using a null and alternative hypothesis:

• Null Hypothesis (H 0 ): The sample data occurs purely from chance.
• Alternative Hypothesis (H A ): The sample data is influenced by some non-random cause.

If the p-value of the hypothesis test is less than some significance level (e.g. α = .05), then we reject the null hypothesis .

Otherwise, if the p-value is not less than some significance level then we fail to reject the null hypothesis .

When writing the conclusion of a hypothesis test, we typically include:

• Whether we reject or fail to reject the null hypothesis.
• The significance level.
• A short explanation in the context of the hypothesis test.

For example, we would write:

We reject the null hypothesis at the 5% significance level.   There is sufficient evidence to support the claim that…

Or, we would write:

We fail to reject the null hypothesis at the 5% significance level.   There is not sufficient evidence to support the claim that…

The following examples show how to write a hypothesis test conclusion in both scenarios.

Example 1: Reject the Null Hypothesis Conclusion

Suppose a biologist believes that a certain fertilizer will cause plants to grow more during a one-month period than they normally do, which is currently 20 inches. To test this, she applies the fertilizer to each of the plants in her laboratory for one month.

She then performs a hypothesis test at a 5% significance level using the following hypotheses:

• H 0 : μ = 20 inches (the fertilizer will have no effect on the mean plant growth)
• H A : μ > 20 inches (the fertilizer will cause mean plant growth to increase)

Suppose the p-value of the test turns out to be 0.002.

Here is how she would report the results of the hypothesis test:

We reject the null hypothesis at the 5% significance level.   There is sufficient evidence to support the claim that this particular fertilizer causes plants to grow more during a one-month period than they normally do.

Example 2: Fail to Reject the Null Hypothesis Conclusion

Suppose the manager of a manufacturing plant wants to test whether or not some new method changes the number of defective widgets produced per month, which is currently 250. To test this, he measures the mean number of defective widgets produced before and after using the new method for one month.

He performs a hypothesis test at a 10% significance level using the following hypotheses:

• H 0 : μ after = μ before (the mean number of defective widgets is the same before and after using the new method)
• H A : μ after ≠ μ before (the mean number of defective widgets produced is different before and after using the new method)

Suppose the p-value of the test turns out to be 0.27.

Here is how he would report the results of the hypothesis test:

We fail to reject the null hypothesis at the 10% significance level.   There is not sufficient evidence to support the claim that the new method leads to a change in the number of defective widgets produced per month.

Additional Resources

The following tutorials provide additional information about hypothesis testing:

Introduction to Hypothesis Testing 4 Examples of Hypothesis Testing in Real Life How to Write a Null Hypothesis

Published by Zach

Leave a reply cancel reply.

Your email address will not be published. Required fields are marked *

How to State the Conclusion about a Hypothesis Test

After you have completed the statistical analysis and decided to reject or fail to reject the Null hypothesis, you need to state your conclusion about the claim. To get the correct wording, you need to recall which hypothesis was the claim.

If the claim was the null, then your conclusion is about whether there was sufficient evidence to reject the claim. Remember, we can never prove the null to be true, but failing to reject it is the next best thing. So, it is not correct to say, “Accept the Null.”

If the claim is the alternative hypothesis, your conclusion can be whether there was sufficient evidence to support (prove) the alternative is true.

Use the following table to help you make a good conclusion.

The best way to state the conclusion is to include the significance level of the test and a bit about the claim itself.

For example, if the claim was the alternative that the mean score on a test was greater than 85, and your decision was to  Reject then Null , then you could conclude: “ At the 5% significance level, there is sufficient evidence to support the claim that the mean score on the test was greater than 85. ”

The reason you should include the significance level is that the decision, and thus the conclusion, could be different if the significance level was not 5%.

If you are curious why we say “Fail to Reject the Null” instead of “Accept the Null,” this short video might be of interest:  Here

2 thoughts on “How to State the Conclusion about a Hypothesis Test”

It is concluded that the null hypothesis Ho is not rejected proportion p is greater than 0.5, at the 0.05 significance

People living in rural Idaho community live longer than 77 years

Leave a Reply Cancel reply

This site uses Akismet to reduce spam. Learn how your comment data is processed .

Have a language expert improve your writing

Run a free plagiarism check in 10 minutes, generate accurate citations for free.

• Knowledge Base

Methodology

• How to Write a Strong Hypothesis | Steps & Examples

How to Write a Strong Hypothesis | Steps & Examples

Published on May 6, 2022 by Shona McCombes . Revised on November 20, 2023.

A hypothesis is a statement that can be tested by scientific research. If you want to test a relationship between two or more variables, you need to write hypotheses before you start your experiment or data collection .

Example: Hypothesis

Daily apple consumption leads to fewer doctor’s visits.

Table of contents

What is a hypothesis, developing a hypothesis (with example), hypothesis examples, other interesting articles, frequently asked questions about writing hypotheses.

A hypothesis states your predictions about what your research will find. It is a tentative answer to your research question that has not yet been tested. For some research projects, you might have to write several hypotheses that address different aspects of your research question.

A hypothesis is not just a guess – it should be based on existing theories and knowledge. It also has to be testable, which means you can support or refute it through scientific research methods (such as experiments, observations and statistical analysis of data).

Variables in hypotheses

Hypotheses propose a relationship between two or more types of variables .

• An independent variable is something the researcher changes or controls.
• A dependent variable is something the researcher observes and measures.

If there are any control variables , extraneous variables , or confounding variables , be sure to jot those down as you go to minimize the chances that research bias  will affect your results.

In this example, the independent variable is exposure to the sun – the assumed cause . The dependent variable is the level of happiness – the assumed effect .

Here's why students love Scribbr's proofreading services

Discover proofreading & editing

Step 1. Ask a question

Writing a hypothesis begins with a research question that you want to answer. The question should be focused, specific, and researchable within the constraints of your project.

Step 2. Do some preliminary research

Your initial answer to the question should be based on what is already known about the topic. Look for theories and previous studies to help you form educated assumptions about what your research will find.

At this stage, you might construct a conceptual framework to ensure that you’re embarking on a relevant topic . This can also help you identify which variables you will study and what you think the relationships are between them. Sometimes, you’ll have to operationalize more complex constructs.

Step 3. Formulate your hypothesis

Now you should have some idea of what you expect to find. Write your initial answer to the question in a clear, concise sentence.

4. Refine your hypothesis

You need to make sure your hypothesis is specific and testable. There are various ways of phrasing a hypothesis, but all the terms you use should have clear definitions, and the hypothesis should contain:

• The relevant variables
• The specific group being studied
• The predicted outcome of the experiment or analysis

5. Phrase your hypothesis in three ways

To identify the variables, you can write a simple prediction in  if…then form. The first part of the sentence states the independent variable and the second part states the dependent variable.

In academic research, hypotheses are more commonly phrased in terms of correlations or effects, where you directly state the predicted relationship between variables.

If you are comparing two groups, the hypothesis can state what difference you expect to find between them.

6. Write a null hypothesis

If your research involves statistical hypothesis testing , you will also have to write a null hypothesis . The null hypothesis is the default position that there is no association between the variables. The null hypothesis is written as H 0 , while the alternative hypothesis is H 1 or H a .

• H 0 : The number of lectures attended by first-year students has no effect on their final exam scores.
• H 1 : The number of lectures attended by first-year students has a positive effect on their final exam scores.

If you want to know more about the research process , methodology , research bias , or statistics , make sure to check out some of our other articles with explanations and examples.

• Sampling methods
• Simple random sampling
• Stratified sampling
• Cluster sampling
• Likert scales
• Reproducibility

 Statistics

• Null hypothesis
• Statistical power
• Probability distribution
• Effect size
• Poisson distribution

Research bias

• Optimism bias
• Cognitive bias
• Implicit bias
• Hawthorne effect
• Anchoring bias
• Explicit bias

Prevent plagiarism. Run a free check.

A hypothesis is not just a guess — it should be based on existing theories and knowledge. It also has to be testable, which means you can support or refute it through scientific research methods (such as experiments, observations and statistical analysis of data).

Null and alternative hypotheses are used in statistical hypothesis testing . The null hypothesis of a test always predicts no effect or no relationship between variables, while the alternative hypothesis states your research prediction of an effect or relationship.

Hypothesis testing is a formal procedure for investigating our ideas about the world using statistics. It is used by scientists to test specific predictions, called hypotheses , by calculating how likely it is that a pattern or relationship between variables could have arisen by chance.

Cite this Scribbr article

If you want to cite this source, you can copy and paste the citation or click the “Cite this Scribbr article” button to automatically add the citation to our free Citation Generator.

McCombes, S. (2023, November 20). How to Write a Strong Hypothesis | Steps & Examples. Scribbr. Retrieved April 2, 2024, from https://www.scribbr.com/methodology/hypothesis/

Is this article helpful?

Shona McCombes

Other students also liked, construct validity | definition, types, & examples, what is a conceptual framework | tips & examples, operationalization | a guide with examples, pros & cons, unlimited academic ai-proofreading.

✔ Document error-free in 5minutes ✔ Unlimited document corrections ✔ Specialized in correcting academic texts

How to Write Hypothesis Test Conclusions (With Examples)

A   hypothesis test is used to test whether or not some hypothesis about a population parameter is true.

To perform a hypothesis test in the real world, researchers obtain a random sample from the population and perform a hypothesis test on the sample data, using a null and alternative hypothesis:

• Null Hypothesis (H 0 ): The sample data occurs purely from chance.
• Alternative Hypothesis (H A ): The sample data is influenced by some non-random cause.

If the p-value of the hypothesis test is less than some significance level (e.g. α = .05), then we reject the null hypothesis .

Otherwise, if the p-value is not less than some significance level then we fail to reject the null hypothesis .

When writing the conclusion of a hypothesis test, we typically include:

• Whether we reject or fail to reject the null hypothesis.
• The significance level.
• A short explanation in the context of the hypothesis test.

For example, we would write:

We reject the null hypothesis at the 5% significance level.   There is sufficient evidence to support the claim that…

Or, we would write:

We fail to reject the null hypothesis at the 5% significance level.   There is not sufficient evidence to support the claim that…

The following examples show how to write a hypothesis test conclusion in both scenarios.

Example 1: Reject the Null Hypothesis Conclusion

Suppose a biologist believes that a certain fertilizer will cause plants to grow more during a one-month period than they normally do, which is currently 20 inches. To test this, she applies the fertilizer to each of the plants in her laboratory for one month.

She then performs a hypothesis test at a 5% significance level using the following hypotheses:

• H 0 : μ = 20 inches (the fertilizer will have no effect on the mean plant growth)
• H A : μ > 20 inches (the fertilizer will cause mean plant growth to increase)

Suppose the p-value of the test turns out to be 0.002.

Here is how she would report the results of the hypothesis test:

We reject the null hypothesis at the 5% significance level.   There is sufficient evidence to support the claim that this particular fertilizer causes plants to grow more during a one-month period than they normally do.

Example 2: Fail to Reject the Null Hypothesis Conclusion

Suppose the manager of a manufacturing plant wants to test whether or not some new method changes the number of defective widgets produced per month, which is currently 250. To test this, he measures the mean number of defective widgets produced before and after using the new method for one month.

He performs a hypothesis test at a 10% significance level using the following hypotheses:

• H 0 : μ after = μ before (the mean number of defective widgets is the same before and after using the new method)
• H A : μ after ≠ μ before (the mean number of defective widgets produced is different before and after using the new method)

Suppose the p-value of the test turns out to be 0.27.

Here is how he would report the results of the hypothesis test:

We fail to reject the null hypothesis at the 10% significance level.   There is not sufficient evidence to support the claim that the new method leads to a change in the number of defective widgets produced per month.

Additional Resources

The following tutorials provide additional information about hypothesis testing:

Introduction to Hypothesis Testing 4 Examples of Hypothesis Testing in Real Life How to Write a Null Hypothesis

10 Examples of Using Probability in Real Life

Mongodb: how to find document by id, related posts, how to normalize data between -1 and 1, vba: how to check if string contains another..., how to interpret f-values in a two-way anova, how to create a vector of ones in..., how to determine if a probability distribution is..., what is a symmetric histogram (definition & examples), how to find the mode of a histogram..., how to find quartiles in even and odd..., how to calculate sxy in statistics (with example), how to calculate expected value of x^3.

Chapter 3: Hypothesis Testing

The previous two chapters introduced methods for organizing and summarizing sample data, and using sample statistics to estimate population parameters. This chapter introduces the next major topic of inferential statistics: hypothesis testing.

A hypothesis is a statement or claim about a property of a population.

The Fundamentals of Hypothesis Testing

When conducting scientific research, typically there is some known information, perhaps from some past work or from a long accepted idea. We want to test whether this claim is believable. This is the basic idea behind a hypothesis test:

• State what we think is true.
• Quantify how confident we are about our claim.
• Use sample statistics to make inferences about population parameters.

For example, past research tells us that the average life span for a hummingbird is about four years. You have been studying the hummingbirds in the southeastern United States and find a sample mean lifespan of 4.8 years. Should you reject the known or accepted information in favor of your results? How confident are you in your estimate? At what point would you say that there is enough evidence to reject the known information and support your alternative claim? How far from the known mean of four years can the sample mean be before we reject the idea that the average lifespan of a hummingbird is four years?

Hypothesis testing is a procedure, based on sample evidence and probability, used to test claims regarding a characteristic of a population.

A hypothesis is a claim or statement about a characteristic of a population of interest to us. A hypothesis test is a way for us to use our sample statistics to test a specific claim.

The population mean weight is known to be 157 lb. We want to test the claim that the mean weight has increased.

Two years ago, the proportion of infected plants was 37%. We believe that a treatment has helped, and we want to test the claim that there has been a reduction in the proportion of infected plants.

Components of a Formal Hypothesis Test

The null hypothesis is a statement about the value of a population parameter, such as the population mean (µ) or the population proportion ( p ). It contains the condition of equality and is denoted as H 0 (H-naught).

H 0 : µ = 157 or H 0 : p = 0.37

The alternative hypothesis is the claim to be tested, the opposite of the null hypothesis. It contains the value of the parameter that we consider plausible and is denoted as H 1 .

H 1 : µ > 157 or H 1 : p ≠ 0.37

The test statistic is a value computed from the sample data that is used in making a decision about the rejection of the null hypothesis. The test statistic converts the sample mean ( x̄ ) or sample proportion ( p̂ ) to a Z- or t-score under the assumption that the null hypothesis is true . It is used to decide whether the difference between the sample statistic and the hypothesized claim is significant.

The p-value is the area under the curve to the left or right of the test statistic. It is compared to the level of significance ( α ).

The critical value is the value that defines the rejection zone (the test statistic values that would lead to rejection of the null hypothesis). It is defined by the level of significance.

The level of significance ( α ) is the probability that the test statistic will fall into the critical region when the null hypothesis is true. This level is set by the researcher.

The conclusion is the final decision of the hypothesis test. The conclusion must always be clearly stated, communicating the decision based on the components of the test. It is important to realize that we never prove or accept the null hypothesis. We are merely saying that the sample evidence is not strong enough to warrant the rejection of the null hypothesis. The conclusion is made up of two parts:

1) Reject or fail to reject the null hypothesis, and 2) there is or is not enough evidence to support the alternative claim.

Option 1) Reject the null hypothesis (H 0 ). This means that you have enough statistical evidence to support the alternative claim (H 1 ).

Option 2) Fail to reject the null hypothesis (H 0 ). This means that you do NOT have enough evidence to support the alternative claim (H 1 ).

Another way to think about hypothesis testing is to compare it to the US justice system. A defendant is innocent until proven guilty (Null hypothesis—innocent). The prosecuting attorney tries to prove that the defendant is guilty (Alternative hypothesis—guilty). There are two possible conclusions that the jury can reach. First, the defendant is guilty (Reject the null hypothesis). Second, the defendant is not guilty (Fail to reject the null hypothesis). This is NOT the same thing as saying the defendant is innocent! In the first case, the prosecutor had enough evidence to reject the null hypothesis (innocent) and support the alternative claim (guilty). In the second case, the prosecutor did NOT have enough evidence to reject the null hypothesis (innocent) and support the alternative claim of guilty.

The Null and Alternative Hypotheses

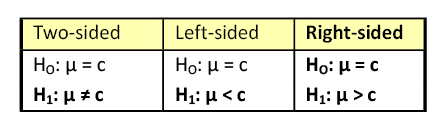
There are three different pairs of null and alternative hypotheses:

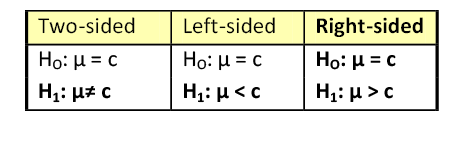
where c is some known value.

A Two-sided Test

This tests whether the population parameter is equal to, versus not equal to, some specific value.

H o : μ = 12 vs. H 1 : μ ≠ 12

The critical region is divided equally into the two tails and the critical values are ± values that define the rejection zones.

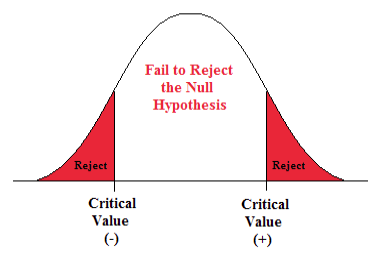
Figure 1. The rejection zone for a two-sided hypothesis test.

A forester studying diameter growth of red pine believes that the mean diameter growth will be different if a fertilization treatment is applied to the stand.

• H o : μ = 1.2 in./ year
• H 1 : μ ≠ 1.2 in./ year

This is a two-sided question, as the forester doesn’t state whether population mean diameter growth will increase or decrease.

A Right-sided Test

This tests whether the population parameter is equal to, versus greater than, some specific value.

H o : μ = 12 vs. H 1 : μ > 12

The critical region is in the right tail and the critical value is a positive value that defines the rejection zone.

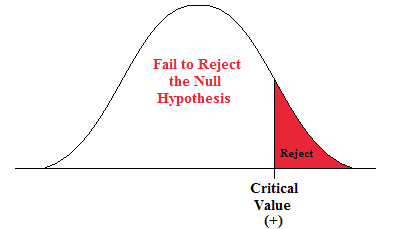
Figure 2. The rejection zone for a right-sided hypothesis test.

A biologist believes that there has been an increase in the mean number of lakes infected with milfoil, an invasive species, since the last study five years ago.

• H o : μ = 15 lakes
• H 1 : μ >15 lakes

This is a right-sided question, as the biologist believes that there has been an increase in population mean number of infected lakes.

A Left-sided Test

This tests whether the population parameter is equal to, versus less than, some specific value.

H o : μ = 12 vs. H 1 : μ < 12

The critical region is in the left tail and the critical value is a negative value that defines the rejection zone.

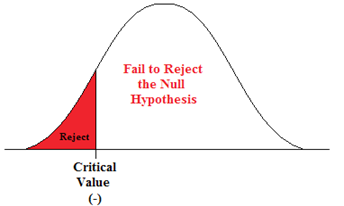
Figure 3. The rejection zone for a left-sided hypothesis test.

A scientist’s research indicates that there has been a change in the proportion of people who support certain environmental policies. He wants to test the claim that there has been a reduction in the proportion of people who support these policies.

• H o : p = 0.57
• H 1 : p < 0.57

This is a left-sided question, as the scientist believes that there has been a reduction in the true population proportion.

Statistically Significant

When the observed results (the sample statistics) are unlikely (a low probability) under the assumption that the null hypothesis is true, we say that the result is statistically significant, and we reject the null hypothesis. This result depends on the level of significance, the sample statistic, sample size, and whether it is a one- or two-sided alternative hypothesis.

Types of Errors

When testing, we arrive at a conclusion of rejecting the null hypothesis or failing to reject the null hypothesis. Such conclusions are sometimes correct and sometimes incorrect (even when we have followed all the correct procedures). We use incomplete sample data to reach a conclusion and there is always the possibility of reaching the wrong conclusion. There are four possible conclusions to reach from hypothesis testing. Of the four possible outcomes, two are correct and two are NOT correct.

Table 1. Possible outcomes from a hypothesis test.

A Type I error is when we reject the null hypothesis when it is true. The symbol α (alpha) is used to represent Type I errors. This is the same alpha we use as the level of significance. By setting alpha as low as reasonably possible, we try to control the Type I error through the level of significance.

A Type II error is when we fail to reject the null hypothesis when it is false. The symbol β (beta) is used to represent Type II errors.

In general, Type I errors are considered more serious. One step in the hypothesis test procedure involves selecting the significance level ( α ), which is the probability of rejecting the null hypothesis when it is correct. So the researcher can select the level of significance that minimizes Type I errors. However, there is a mathematical relationship between α, β , and n (sample size).

• As α increases, β decreases
• As α decreases, β increases
• As sample size increases (n), both α and β decrease

The natural inclination is to select the smallest possible value for α, thinking to minimize the possibility of causing a Type I error. Unfortunately, this forces an increase in Type II errors. By making the rejection zone too small, you may fail to reject the null hypothesis, when, in fact, it is false. Typically, we select the best sample size and level of significance, automatically setting β .

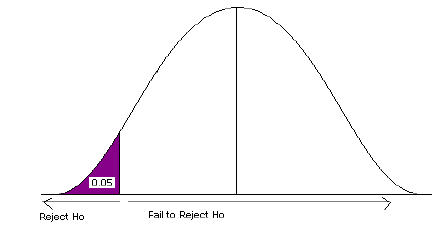
Figure 4. Type 1 error.

Power of the Test

A Type II error ( β ) is the probability of failing to reject a false null hypothesis. It follows that 1- β is the probability of rejecting a false null hypothesis. This probability is identified as the power of the test, and is often used to gauge the test’s effectiveness in recognizing that a null hypothesis is false.

The probability that at a fixed level α significance test will reject H 0 , when a particular alternative value of the parameter is true is called the power of the test.

Power is also directly linked to sample size. For example, suppose the null hypothesis is that the mean fish weight is 8.7 lb. Given sample data, a level of significance of 5%, and an alternative weight of 9.2 lb., we can compute the power of the test to reject μ = 8.7 lb. If we have a small sample size, the power will be low. However, increasing the sample size will increase the power of the test. Increasing the level of significance will also increase power. A 5% test of significance will have a greater chance of rejecting the null hypothesis than a 1% test because the strength of evidence required for the rejection is less. Decreasing the standard deviation has the same effect as increasing the sample size: there is more information about μ .

Hypothesis Test about the Population Mean ( μ ) when the Population Standard Deviation ( σ ) is Known

We are going to examine two equivalent ways to perform a hypothesis test: the classical approach and the p-value approach. The classical approach is based on standard deviations. This method compares the test statistic (Z-score) to a critical value (Z-score) from the standard normal table. If the test statistic falls in the rejection zone, you reject the null hypothesis. The p-value approach is based on area under the normal curve. This method compares the area associated with the test statistic to alpha ( α ), the level of significance (which is also area under the normal curve). If the p-value is less than alpha, you would reject the null hypothesis.

As a past student poetically said: If the p-value is a wee value, Reject Ho

Both methods must have:

• Data from a random sample.
• Verification of the assumption of normality.
• A null and alternative hypothesis.
• A criterion that determines if we reject or fail to reject the null hypothesis.
• A conclusion that answers the question.

There are four steps required for a hypothesis test:

• State the null and alternative hypotheses.
• State the level of significance and the critical value.
• Compute the test statistic.
• State a conclusion.

The Classical Method for Testing a Claim about the Population Mean ( μ ) when the Population Standard Deviation ( σ ) is Known

A forester studying diameter growth of red pine believes that the mean diameter growth will be different from the known mean growth of 1.35 inches/year if a fertilization treatment is applied to the stand. He conducts his experiment, collects data from a sample of 32 plots, and gets a sample mean diameter growth of 1.6 in./year. The population standard deviation for this stand is known to be 0.46 in./year. Does he have enough evidence to support his claim?

Step 1) State the null and alternative hypotheses.

• H o : μ = 1.35 in./year
• H 1 : μ ≠ 1.35 in./year

Step 2) State the level of significance and the critical value.

• We will choose a level of significance of 5% ( α = 0.05).
• For a two-sided question, we need a two-sided critical value – Z α /2 and + Z α /2 .
• The level of significance is divided by 2 (since we are only testing “not equal”). We must have two rejection zones that can deal with either a greater than or less than outcome (to the right (+) or to the left (-)).
• We need to find the Z-score associated with the area of 0.025. The red areas are equal to α /2 = 0.05/2 = 0.025 or 2.5% of the area under the normal curve.
• Go into the body of values and find the negative Z-score associated with the area 0.025.

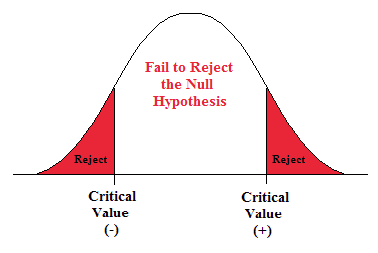
Figure 5. The rejection zone for a two-sided test.

• The negative critical value is -1.96. Since the curve is symmetric, we know that the positive critical value is 1.96.
• ±1.96 are the critical values. These values set up the rejection zone. If the test statistic falls within these red rejection zones, we reject the null hypothesis.

Step 3) Compute the test statistic.

• The test statistic is the number of standard deviations the sample mean is from the known mean. It is also a Z-score, just like the critical value.

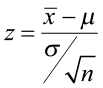
• For this problem, the test statistic is

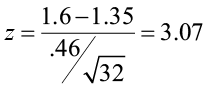
Step 4) State a conclusion.

• Compare the test statistic to the critical value. If the test statistic falls into the rejection zones, reject the null hypothesis. In other words, if the test statistic is greater than +1.96 or less than -1.96, reject the null hypothesis.

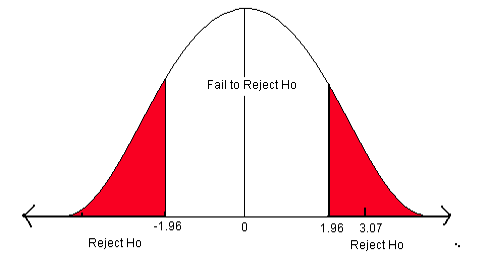
Figure 6. The critical values for a two-sided test when α = 0.05.

In this problem, the test statistic falls in the red rejection zone. The test statistic of 3.07 is greater than the critical value of 1.96.We will reject the null hypothesis. We have enough evidence to support the claim that the mean diameter growth is different from (not equal to) 1.35 in./year.

A researcher believes that there has been an increase in the average farm size in his state since the last study five years ago. The previous study reported a mean size of 450 acres with a population standard deviation ( σ ) of 167 acres. He samples 45 farms and gets a sample mean of 485.8 acres. Is there enough information to support his claim?

• H o : μ = 450 acres
• H 1 : μ >450 acres
• For a one-sided question, we need a one-sided positive critical value Z α .
• The level of significance is all in the right side (the rejection zone is just on the right side).
• We need to find the Z-score associated with the 5% area in the right tail.

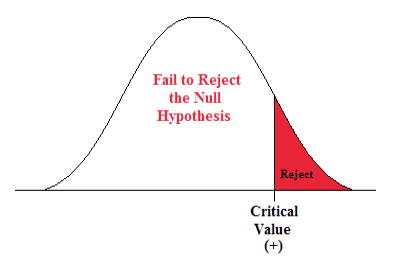
Figure 7. Rejection zone for a right-sided hypothesis test.

• Go into the body of values in the standard normal table and find the Z-score that separates the lower 95% from the upper 5%.
• The critical value is 1.645. This value sets up the rejection zone.

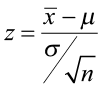
• Compare the test statistic to the critical value.

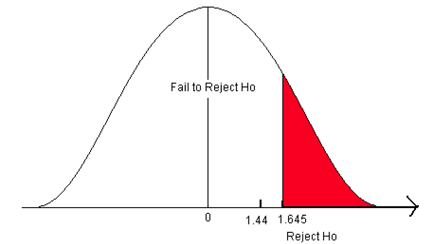
Figure 8. The critical value for a right-sided test when α = 0.05.

• The test statistic does not fall in the rejection zone. It is less than the critical value.

We fail to reject the null hypothesis. We do not have enough evidence to support the claim that the mean farm size has increased from 450 acres.

A researcher believes that there has been a reduction in the mean number of hours that college students spend preparing for final exams. A national study stated that students at a 4-year college spend an average of 23 hours preparing for 5 final exams each semester with a population standard deviation of 7.3 hours. The researcher sampled 227 students and found a sample mean study time of 19.6 hours. Does this indicate that the average study time for final exams has decreased? Use a 1% level of significance to test this claim.

• H o : μ = 23 hours
• H 1 : μ < 23 hours
• This is a left-sided test so alpha (0.01) is all in the left tail.

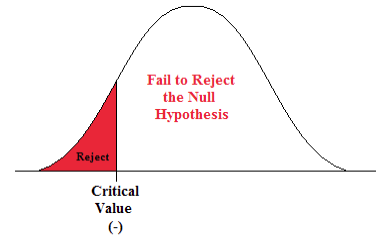
Figure 9. The rejection zone for a left-sided hypothesis test.

• Go into the body of values in the standard normal table and find the Z-score that defines the lower 1% of the area.
• The critical value is -2.33. This value sets up the rejection zone.

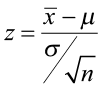
Figure 10. The critical value for a left-sided test when α = 0.01.

• The test statistic falls in the rejection zone. The test statistic of -7.02 is less than the critical value of -2.33.

We reject the null hypothesis. We have sufficient evidence to support the claim that the mean final exam study time has decreased below 23 hours.

Testing a Hypothesis using P-values

The p-value is the probability of observing our sample mean given that the null hypothesis is true. It is the area under the curve to the left or right of the test statistic. If the probability of observing such a sample mean is very small (less than the level of significance), we would reject the null hypothesis. Computations for the p-value depend on whether it is a one- or two-sided test.

Steps for a hypothesis test using p-values:

• State the level of significance.
• Compute the test statistic and find the area associated with it (this is the p-value).
• Compare the p-value to alpha ( α ) and state a conclusion.

Instead of comparing Z-score test statistic to Z-score critical value, as in the classical method, we compare area of the test statistic to area of the level of significance.

The Decision Rule: If the p-value is less than alpha, we reject the null hypothesis

Computing P-values

If it is a two-sided test (the alternative claim is ≠), the p-value is equal to two times the probability of the absolute value of the test statistic. If the test is a left-sided test (the alternative claim is “<”), then the p-value is equal to the area to the left of the test statistic. If the test is a right-sided test (the alternative claim is “>”), then the p-value is equal to the area to the right of the test statistic.

Let’s look at Example 6 again.

A forester studying diameter growth of red pine believes that the mean diameter growth will be different from the known mean growth of 1.35 in./year if a fertilization treatment is applied to the stand. He conducts his experiment, collects data from a sample of 32 plots, and gets a sample mean diameter growth of 1.6 in./year. The population standard deviation for this stand is known to be 0.46 in./year. Does he have enough evidence to support his claim?

Step 2) State the level of significance.

• For this problem, the test statistic is:

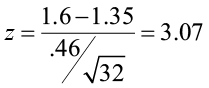
The p-value is two times the area of the absolute value of the test statistic (because the alternative claim is “not equal”).

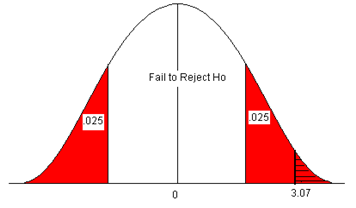
Figure 11. The p-value compared to the level of significance.

• Look up the area for the Z-score 3.07 in the standard normal table. The area (probability) is equal to 1 – 0.9989 = 0.0011.
• Multiply this by 2 to get the p-value = 2 * 0.0011 = 0.0022.

Step 4) Compare the p-value to alpha and state a conclusion.

• Use the Decision Rule (if the p-value is less than α , reject H 0 ).
• In this problem, the p-value (0.0022) is less than alpha (0.05).
• We reject the H 0 . We have enough evidence to support the claim that the mean diameter growth is different from 1.35 inches/year.

Let’s look at Example 7 again.

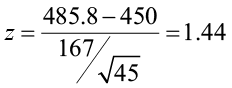
The p-value is the area to the right of the Z-score 1.44 (the hatched area).

• This is equal to 1 – 0.9251 = 0.0749.
• The p-value is 0.0749.

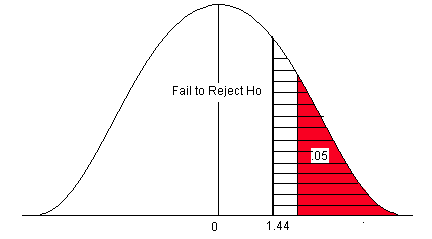
Figure 12. The p-value compared to the level of significance for a right-sided test.

• Use the Decision Rule.
• In this problem, the p-value (0.0749) is greater than alpha (0.05), so we Fail to Reject the H 0 .
• The area of the test statistic is greater than the area of alpha ( α ).

We fail to reject the null hypothesis. We do not have enough evidence to support the claim that the mean farm size has increased.

Let’s look at Example 8 again.

• H 0 : μ = 23 hours

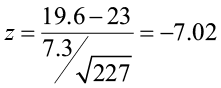
The p-value is the area to the left of the test statistic (the little black area to the left of -7.02). The Z-score of -7.02 is not on the standard normal table. The smallest probability on the table is 0.0002. We know that the area for the Z-score -7.02 is smaller than this area (probability). Therefore, the p-value is <0.0002.

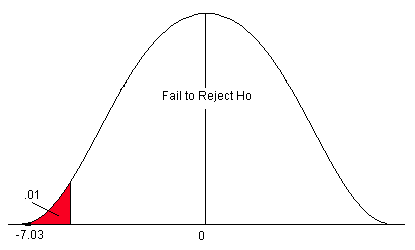
Figure 13. The p-value compared to the level of significance for a left-sided test.

• In this problem, the p-value (p<0.0002) is less than alpha (0.01), so we Reject the H 0 .
• The area of the test statistic is much less than the area of alpha ( α ).

We reject the null hypothesis. We have enough evidence to support the claim that the mean final exam study time has decreased below 23 hours.

Both the classical method and p-value method for testing a hypothesis will arrive at the same conclusion. In the classical method, the critical Z-score is the number on the z-axis that defines the level of significance ( α ). The test statistic converts the sample mean to units of standard deviation (a Z-score). If the test statistic falls in the rejection zone defined by the critical value, we will reject the null hypothesis. In this approach, two Z-scores, which are numbers on the z-axis, are compared. In the p-value approach, the p-value is the area associated with the test statistic. In this method, we compare α (which is also area under the curve) to the p-value. If the p-value is less than α , we reject the null hypothesis. The p-value is the probability of observing such a sample mean when the null hypothesis is true. If the probability is too small (less than the level of significance), then we believe we have enough statistical evidence to reject the null hypothesis and support the alternative claim.

Software Solutions

(referring to Ex. 8)

One-Sample Z

Excel does not offer 1-sample hypothesis testing.

Hypothesis Test about the Population Mean ( μ ) when the Population Standard Deviation ( σ ) is Unknown

Frequently, the population standard deviation (σ) is not known. We can estimate the population standard deviation (σ) with the sample standard deviation (s). However, the test statistic will no longer follow the standard normal distribution. We must rely on the student’s t-distribution with n-1 degrees of freedom. Because we use the sample standard deviation (s), the test statistic will change from a Z-score to a t-score.

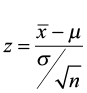
Steps for a hypothesis test are the same that we covered in Section 2.

Just as with the hypothesis test from the previous section, the data for this test must be from a random sample and requires either that the population from which the sample was drawn be normal or that the sample size is sufficiently large (n≥30). A t-test is robust, so small departures from normality will not adversely affect the results of the test. That being said, if the sample size is smaller than 30, it is always good to verify the assumption of normality through a normal probability plot.

We will still have the same three pairs of null and alternative hypotheses and we can still use either the classical approach or the p-value approach.

Selecting the correct critical value from the student’s t-distribution table depends on three factors: the type of test (one-sided or two-sided alternative hypothesis), the sample size, and the level of significance.

For a two-sided test (“not equal” alternative hypothesis), the critical value (t α /2 ), is determined by alpha ( α ), the level of significance, divided by two, to deal with the possibility that the result could be less than OR greater than the known value.

• If your level of significance was 0.05, you would use the 0.025 column to find the correct critical value (0.05/2 = 0.025).
• If your level of significance was 0.01, you would use the 0.005 column to find the correct critical value (0.01/2 = 0.005).

For a one-sided test (“a less than” or “greater than” alternative hypothesis), the critical value (t α ) , is determined by alpha ( α ), the level of significance, being all in the one side.

• If your level of significance was 0.05, you would use the 0.05 column to find the correct critical value for either a left or right-side question. If you are asking a “less than” (left-sided question, your critical value will be negative. If you are asking a “greater than” (right-sided question), your critical value will be positive.

Find the critical value you would use to test the claim that μ ≠ 112 with a sample size of 18 and a 5% level of significance.

In this case, the critical value (t α /2 ) would be 2.110. This is a two-sided question (≠) so you would divide alpha by 2 (0.05/2 = 0.025) and go down the 0.025 column to 17 degrees of freedom.

What would the critical value be if you wanted to test that μ < 112 for the same data?

In this case, the critical value would be 1.740. This is a one-sided question (<) so alpha would be divided by 1 (0.05/1 = 0.05). You would go down the 0.05 column with 17 degrees of freedom to get the correct critical value.

In 2005, the mean pH level of rain in a county in northern New York was 5.41. A biologist believes that the rain acidity has changed. He takes a random sample of 11 rain dates in 2010 and obtains the following data. Use a 1% level of significance to test his claim.

4.70, 5.63, 5.02, 5.78, 4.99, 5.91, 5.76, 5.54, 5.25, 5.18, 5.01

The sample size is small and we don’t know anything about the distribution of the population, so we examine a normal probability plot. The distribution looks normal so we will continue with our test.

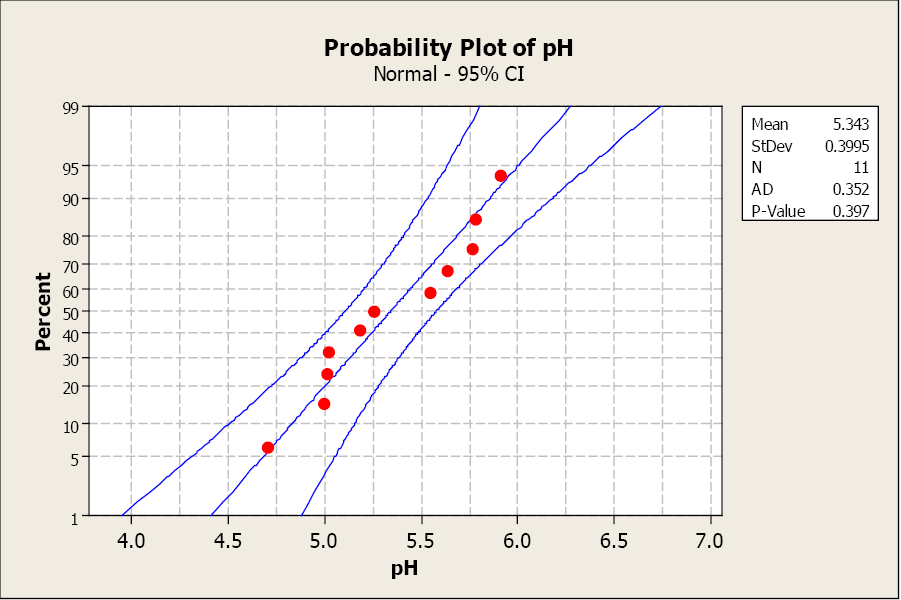
Figure 14. A normal probability plot for Example 9.

The sample mean is 5.343 with a sample standard deviation of 0.397.

• H o : μ = 5.41
• H 1 : μ ≠ 5.41
• This is a two-sided question so alpha is divided by two.

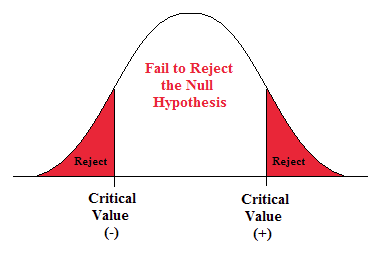
Figure 15. The rejection zones for a two-sided test.

• t α /2 is found by going down the 0.005 column with 14 degrees of freedom.
• t α /2 = ±3.169.
• The test statistic is a t-score.

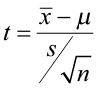
Figure 16. The critical values for a two-sided test when α = 0.01.

• The test statistic does not fall in the rejection zone.

We will fail to reject the null hypothesis. We do not have enough evidence to support the claim that the mean rain pH has changed.

A One-sided Test

Cadmium, a heavy metal, is toxic to animals. Mushrooms, however, are able to absorb and accumulate cadmium at high concentrations. The government has set safety limits for cadmium in dry vegetables at 0.5 ppm. Biologists believe that the mean level of cadmium in mushrooms growing near strip mines is greater than the recommended limit of 0.5 ppm, negatively impacting the animals that live in this ecosystem. A random sample of 51 mushrooms gave a sample mean of 0.59 ppm with a sample standard deviation of 0.29 ppm. Use a 5% level of significance to test the claim that the mean cadmium level is greater than the acceptable limit of 0.5 ppm.

The sample size is greater than 30 so we are assured of a normal distribution of the means.

• H o : μ = 0.5 ppm
• H 1 : μ > 0.5 ppm
• This is a right-sided question so alpha is all in the right tail.

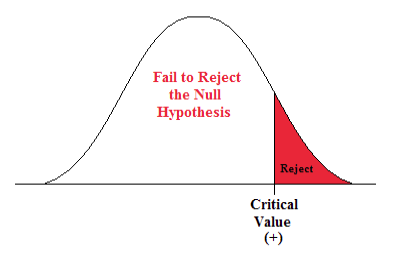
Figure 17. Rejection zone for a right-sided test.

• t α is found by going down the 0.05 column with 50 degrees of freedom.
• t α = 1.676

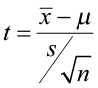
Step 4) State a Conclusion.

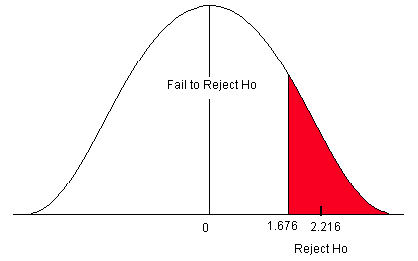
Figure 18. Critical value for a right-sided test when α = 0.05.

The test statistic falls in the rejection zone. We will reject the null hypothesis. We have enough evidence to support the claim that the mean cadmium level is greater than the acceptable safe limit.

BUT, what happens if the significance level changes to 1%?

The critical value is now found by going down the 0.01 column with 50 degrees of freedom. The critical value is 2.403. The test statistic is now LESS THAN the critical value. The test statistic does not fall in the rejection zone. The conclusion will change. We do NOT have enough evidence to support the claim that the mean cadmium level is greater than the acceptable safe limit of 0.5 ppm.

The level of significance is the probability that you, as the researcher, set to decide if there is enough statistical evidence to support the alternative claim. It should be set before the experiment begins.

P-value Approach

We can also use the p-value approach for a hypothesis test about the mean when the population standard deviation ( σ ) is unknown. However, when using a student’s t-table, we can only estimate the range of the p-value, not a specific value as when using the standard normal table. The student’s t-table has area (probability) across the top row in the table, with t-scores in the body of the table.

• To find the p-value (the area associated with the test statistic), you would go to the row with the number of degrees of freedom.
• Go across that row until you find the two values that your test statistic is between, then go up those columns to find the estimated range for the p-value.

Estimating P-value from a Student’s T-table

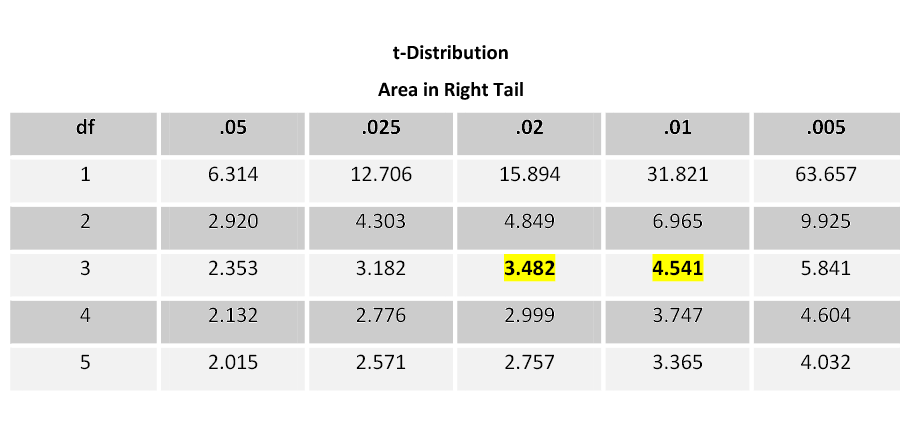
If your test statistic is 3.789 with 3 degrees of freedom, you would go across the 3 df row. The value 3.789 falls between the values 3.482 and 4.541 in that row. Therefore, the p-value is between 0.02 and 0.01. The p-value will be greater than 0.01 but less than 0.02 (0.01<p<0.02).

If your level of significance is 5%, you would reject the null hypothesis as the p-value (0.01-0.02) is less than alpha ( α ) of 0.05.

If your level of significance is 1%, you would fail to reject the null hypothesis as the p-value (0.01-0.02) is greater than alpha ( α ) of 0.01.

Software packages typically output p-values. It is easy to use the Decision Rule to answer your research question by the p-value method.

(referring to Ex. 12)

One-Sample T

Test of mu = 0.5 vs. > 0.5

Additional example: www.youtube.com/watch?v=WwdSjO4VUsg .

Hypothesis Test for a Population Proportion ( p )

Frequently, the parameter we are testing is the population proportion.

• We are studying the proportion of trees with cavities for wildlife habitat.
• We need to know if the proportion of people who support green building materials has changed.
• Has the proportion of wolves that died last year in Yellowstone increased from the year before?

Recall that the best point estimate of p , the population proportion, is given by

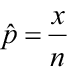
when np (1 – p )≥10. We can use both the classical approach and the p-value approach for testing.

The steps for a hypothesis test are the same that we covered in Section 2.

The test statistic follows the standard normal distribution. Notice that the standard error (the denominator) uses p instead of p̂ , which was used when constructing a confidence interval about the population proportion. In a hypothesis test, the null hypothesis is assumed to be true, so the known proportion is used.

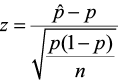
• The critical value comes from the standard normal table, just as in Section 2. We will still use the same three pairs of null and alternative hypotheses as we used in the previous sections, but the parameter is now p instead of μ :

• For a two-sided test, alpha will be divided by 2 giving a ± Z α /2 critical value.
• For a left-sided test, alpha will be all in the left tail giving a – Z α critical value.
• For a right-sided test, alpha will be all in the right tail giving a Z α critical value.

A botanist has produced a new variety of hybrid soy plant that is better able to withstand drought than other varieties. The botanist knows the seed germination for the parent plants is 75%, but does not know the seed germination for the new hybrid. He tests the claim that it is different from the parent plants. To test this claim, 450 seeds from the hybrid plant are tested and 321 have germinated. Use a 5% level of significance to test this claim that the germination rate is different from 75%.

• H o : p = 0.75
• H 1 : p ≠ 0.75

This is a two-sided question so alpha is divided by 2.

• Alpha is 0.05 so the critical values are ± Z α /2 = ± Z .025 .
• Look on the negative side of the standard normal table, in the body of values for 0.025.
• The critical values are ± 1.96.

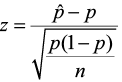
Figure 19. Critical values for a two-sided test when α = 0.05.

The test statistic does not fall in the rejection zone. We fail to reject the null hypothesis. We do not have enough evidence to support the claim that the germination rate of the hybrid plant is different from the parent plants.

Let’s answer this question using the p-value approach. Remember, for a two-sided alternative hypothesis (“not equal”), the p-value is two times the area of the test statistic. The test statistic is -1.81 and we want to find the area to the left of -1.81 from the standard normal table.

• On the negative page, find the Z-score -1.81. Find the area associated with this Z-score.
• The area = 0.0351.
• This is a two-sided test so multiply the area times 2 to get the p-value = 0.0351 x 2 = 0.0702.

Now compare the p-value to alpha. The Decision Rule states that if the p-value is less than alpha, reject the H 0 . In this case, the p-value (0.0702) is greater than alpha (0.05) so we will fail to reject H 0 . We do not have enough evidence to support the claim that the germination rate of the hybrid plant is different from the parent plants.

You are a biologist studying the wildlife habitat in the Monongahela National Forest. Cavities in older trees provide excellent habitat for a variety of birds and small mammals. A study five years ago stated that 32% of the trees in this forest had suitable cavities for this type of wildlife. You believe that the proportion of cavity trees has increased. You sample 196 trees and find that 79 trees have cavities. Does this evidence support your claim that there has been an increase in the proportion of cavity trees?

Use a 10% level of significance to test this claim.

• H o : p = 0.32
• H 1 : p > 0.32

This is a one-sided question so alpha is divided by 1.

• Alpha is 0.10 so the critical value is Z α = Z .10
• Look on the positive side of the standard normal table, in the body of values for 0.90.
• The critical value is 1.28.

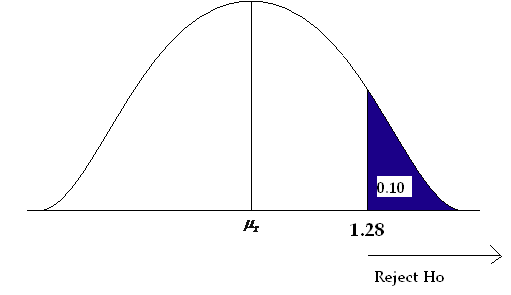
Figure 20. Critical value for a right-sided test where α = 0.10.

• The test statistic is the number of standard deviations the sample proportion is from the known proportion. It is also a Z-score, just like the critical value.

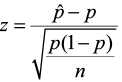
Figure 21. Comparison of the test statistic and the critical value.

The test statistic is larger than the critical value (it falls in the rejection zone). We will reject the null hypothesis. We have enough evidence to support the claim that there has been an increase in the proportion of cavity trees.

Now use the p-value approach to answer the question. This is a right-sided question (“greater than”), so the p-value is equal to the area to the right of the test statistic. Go to the positive side of the standard normal table and find the area associated with the Z-score of 2.49. The area is 0.9936. Remember that this table is cumulative from the left. To find the area to the right of 2.49, we subtract from one.

p-value = (1 – 0.9936) = 0.0064

The p-value is less than the level of significance (0.10), so we reject the null hypothesis. We have enough evidence to support the claim that the proportion of cavity trees has increased.

(referring to Ex. 15)

Test and CI for One Proportion

Test of p = 0.32 vs. p > 0.32

Hypothesis Test about a Variance

When people think of statistical inference, they usually think of inferences involving population means or proportions. However, the particular population parameter needed to answer an experimenter’s practical questions varies from one situation to another, and sometimes a population’s variability is more important than its mean. Thus, product quality is often defined in terms of low variability.

Sample variance S 2 can be used for inferences concerning a population variance σ 2 . For a random sample of n measurements drawn from a normal population with mean μ and variance σ 2 , the value S 2 provides a point estimate for σ 2 . In addition, the quantity ( n – 1) S 2 / σ 2 follows a Chi-square ( χ 2 ) distribution, with df = n – 1.

The properties of Chi-square ( χ 2 ) distribution are:

• Unlike Z and t distributions, the values in a chi-square distribution are all positive.
• The chi-square distribution is asymmetric, unlike the Z and t distributions.
• There are many chi-square distributions. We obtain a particular one by specifying the degrees of freedom (df = n – 1) associated with the sample variances S 2 .

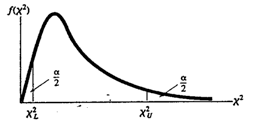
Figure 22. The chi-square distribution.

One-sample χ 2 test for testing the hypotheses:

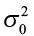
Alternative hypothesis:

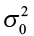
where the χ 2 critical value in the rejection region is based on degrees of freedom df = n – 1 and a specified significance level of α .

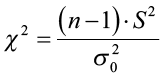
As with previous sections, if the test statistic falls in the rejection zone set by the critical value, you will reject the null hypothesis.

A forester wants to control a dense understory of striped maple that is interfering with desirable hardwood regeneration using a mist blower to apply an herbicide treatment. She wants to make sure that treatment has a consistent application rate, in other words, low variability not exceeding 0.25 gal./acre (0.06 gal. 2 ). She collects sample data (n = 11) on this type of mist blower and gets a sample variance of 0.064 gal. 2 Using a 5% level of significance, test the claim that the variance is significantly greater than 0.06 gal. 2

H 0 : σ 2 = 0.06

H 1 : σ 2 >0.06

The critical value is 18.307. Any test statistic greater than this value will cause you to reject the null hypothesis.

The test statistic is

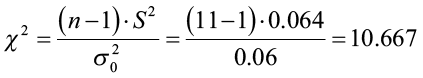
We fail to reject the null hypothesis. The forester does NOT have enough evidence to support the claim that the variance is greater than 0.06 gal. 2 You can also estimate the p-value using the same method as for the student t-table. Go across the row for degrees of freedom until you find the two values that your test statistic falls between. In this case going across the row 10, the two table values are 4.865 and 15.987. Now go up those two columns to the top row to estimate the p-value (0.1-0.9). The p-value is greater than 0.1 and less than 0.9. Both are greater than the level of significance (0.05) causing us to fail to reject the null hypothesis.

(referring to Ex. 16)

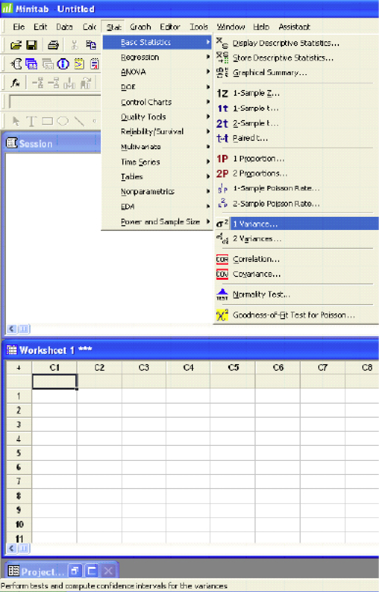
Test and CI for One Variance

The chi-square method is only for the normal distribution.

Excel does not offer 1-sample χ 2 testing.

Putting it all Together Using the Classical Method

To test a claim about μ when σ is known.

• Write the null and alternative hypotheses.
• State the level of significance and get the critical value from the standard normal table.

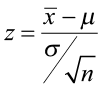
• Compare the test statistic to the critical value (Z-score) and write the conclusion.

To Test a Claim about μ When σ is Unknown

• State the level of significance and get the critical value from the student’s t-table with n-1 degrees of freedom.

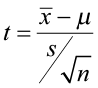
• Compare the test statistic to the critical value (t-score) and write the conclusion.

To Test a Claim about p

• State the level of significance and get the critical value from the standard normal distribution.

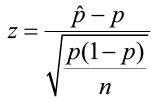
Table 4. A summary table for critical Z-scores.

To Test a Claim about Variance

• State the level of significance and get the critical value from the chi-square table using n-1 degrees of freedom.

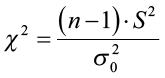
• Compare the test statistic to the critical value and write the conclusion.
• Natural Resources Biometrics. Authored by : Diane Kiernan. Located at : https://textbooks.opensuny.org/natural-resources-biometrics/ . Project : Open SUNY Textbooks. License : CC BY-NC-SA: Attribution-NonCommercial-ShareAlike

Privacy Policy

• The Open University
• Guest user / Sign out
• Study with The Open University

My OpenLearn Profile

Personalise your OpenLearn profile, save your favourite content and get recognition for your learning

About this free course

Become an ou student, download this course, share this free course.

Start this free course now. Just create an account and sign in. Enrol and complete the course for a free statement of participation or digital badge if available.

The purpose of this course was to discuss hypotheses testing. Through the activities, you have gained a better understanding of the concept of alpha (α). You have learned the difference between a one-tailed test and a two-tailed test. Additionally, you have learned how to calculate z-scores and p-values as well as how to use them to determine whether null hypotheses should be accepted or rejected. Finally, the end of this course helped you gain an understanding of how to conduct hypothesis testing for population proportions.

A second OpenLearn course on data analysis, Data analysis: visualisations in Excel [ Tip: hold Ctrl and click a link to open it in a new tab. ( Hide tip ) ] , is now also available should you wish to take your studies further.

This OpenLearn course is an adapted extract from the Open University course B126 Business data analytics and decision making .

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons
• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

4.4: Hypothesis Testing

• Last updated
• Save as PDF
• Page ID 283

• David Diez, Christopher Barr, & Mine Çetinkaya-Rundel
• OpenIntro Statistics

Is the typical US runner getting faster or slower over time? We consider this question in the context of the Cherry Blossom Run, comparing runners in 2006 and 2012. Technological advances in shoes, training, and diet might suggest runners would be faster in 2012. An opposing viewpoint might say that with the average body mass index on the rise, people tend to run slower. In fact, all of these components might be influencing run time.

In addition to considering run times in this section, we consider a topic near and dear to most students: sleep. A recent study found that college students average about 7 hours of sleep per night.15 However, researchers at a rural college are interested in showing that their students sleep longer than seven hours on average. We investigate this topic in Section 4.3.4.

Hypothesis Testing Framework

The average time for all runners who finished the Cherry Blossom Run in 2006 was 93.29 minutes (93 minutes and about 17 seconds). We want to determine if the run10Samp data set provides strong evidence that the participants in 2012 were faster or slower than those runners in 2006, versus the other possibility that there has been no change. 16 We simplify these three options into two competing hypotheses :

• H 0 : The average 10 mile run time was the same for 2006 and 2012.
• H A : The average 10 mile run time for 2012 was different than that of 2006.

We call H 0 the null hypothesis and H A the alternative hypothesis.

Null and alternative hypotheses

• The null hypothesis (H 0 ) often represents either a skeptical perspective or a claim to be tested.
• The alternative hypothesis (H A ) represents an alternative claim under consideration and is often represented by a range of possible parameter values.

15 theloquitur.com/?p=1161

16 While we could answer this question by examining the entire population data (run10), we only consider the sample data (run10Samp), which is more realistic since we rarely have access to population data.

The null hypothesis often represents a skeptical position or a perspective of no difference. The alternative hypothesis often represents a new perspective, such as the possibility that there has been a change.

Hypothesis testing framework

The skeptic will not reject the null hypothesis (H 0 ), unless the evidence in favor of the alternative hypothesis (H A ) is so strong that she rejects H 0 in favor of H A .

The hypothesis testing framework is a very general tool, and we often use it without a second thought. If a person makes a somewhat unbelievable claim, we are initially skeptical. However, if there is sufficient evidence that supports the claim, we set aside our skepticism and reject the null hypothesis in favor of the alternative. The hallmarks of hypothesis testing are also found in the US court system.

Exercise \(\PageIndex{1}\)

A US court considers two possible claims about a defendant: she is either innocent or guilty. If we set these claims up in a hypothesis framework, which would be the null hypothesis and which the alternative? 17

Jurors examine the evidence to see whether it convincingly shows a defendant is guilty. Even if the jurors leave unconvinced of guilt beyond a reasonable doubt, this does not mean they believe the defendant is innocent. This is also the case with hypothesis testing: even if we fail to reject the null hypothesis, we typically do not accept the null hypothesis as true. Failing to find strong evidence for the alternative hypothesis is not equivalent to accepting the null hypothesis.

17 H 0 : The average cost is $650 per month, \(\mu\) = $650.

In the example with the Cherry Blossom Run, the null hypothesis represents no difference in the average time from 2006 to 2012. The alternative hypothesis represents something new or more interesting: there was a difference, either an increase or a decrease. These hypotheses can be described in mathematical notation using \(\mu_{12}\) as the average run time for 2012:

• H 0 : \(\mu_{12} = 93.29\)
• H A : \(\mu_{12} \ne 93.29\)

where 93.29 minutes (93 minutes and about 17 seconds) is the average 10 mile time for all runners in the 2006 Cherry Blossom Run. Using this mathematical notation, the hypotheses can now be evaluated using statistical tools. We call 93.29 the null value since it represents the value of the parameter if the null hypothesis is true. We will use the run10Samp data set to evaluate the hypothesis test.

Testing Hypotheses using Confidence Intervals

We can start the evaluation of the hypothesis setup by comparing 2006 and 2012 run times using a point estimate from the 2012 sample: \(\bar {x}_{12} = 95.61\) minutes. This estimate suggests the average time is actually longer than the 2006 time, 93.29 minutes. However, to evaluate whether this provides strong evidence that there has been a change, we must consider the uncertainty associated with \(\bar {x}_{12}\).

1 6 The jury considers whether the evidence is so convincing (strong) that there is no reasonable doubt regarding the person's guilt; in such a case, the jury rejects innocence (the null hypothesis) and concludes the defendant is guilty (alternative hypothesis).

We learned in Section 4.1 that there is fluctuation from one sample to another, and it is very unlikely that the sample mean will be exactly equal to our parameter; we should not expect \(\bar {x}_{12}\) to exactly equal \(\mu_{12}\). Given that \(\bar {x}_{12} = 95.61\), it might still be possible that the population average in 2012 has remained unchanged from 2006. The difference between \(\bar {x}_{12}\) and 93.29 could be due to sampling variation, i.e. the variability associated with the point estimate when we take a random sample.

In Section 4.2, confidence intervals were introduced as a way to find a range of plausible values for the population mean. Based on run10Samp, a 95% confidence interval for the 2012 population mean, \(\mu_{12}\), was calculated as

\[(92.45, 98.77)\]

Because the 2006 mean, 93.29, falls in the range of plausible values, we cannot say the null hypothesis is implausible. That is, we failed to reject the null hypothesis, H 0 .

Double negatives can sometimes be used in statistics

In many statistical explanations, we use double negatives. For instance, we might say that the null hypothesis is not implausible or we failed to reject the null hypothesis. Double negatives are used to communicate that while we are not rejecting a position, we are also not saying it is correct.

Example \(\PageIndex{1}\)

Next consider whether there is strong evidence that the average age of runners has changed from 2006 to 2012 in the Cherry Blossom Run. In 2006, the average age was 36.13 years, and in the 2012 run10Samp data set, the average was 35.05 years with a standard deviation of 8.97 years for 100 runners.

First, set up the hypotheses:

• H 0 : The average age of runners has not changed from 2006 to 2012, \(\mu_{age} = 36.13.\)
• H A : The average age of runners has changed from 2006 to 2012, \(\mu _{age} 6 \ne 36.13.\)

We have previously veri ed conditions for this data set. The normal model may be applied to \(\bar {y}\) and the estimate of SE should be very accurate. Using the sample mean and standard error, we can construct a 95% con dence interval for \(\mu _{age}\) to determine if there is sufficient evidence to reject H 0 :

\[\bar{y} \pm 1.96 \times \dfrac {s}{\sqrt {100}} \rightarrow 35.05 \pm 1.96 \times 0.90 \rightarrow (33.29, 36.81)\]

This confidence interval contains the null value, 36.13. Because 36.13 is not implausible, we cannot reject the null hypothesis. We have not found strong evidence that the average age is different than 36.13 years.

Exercise \(\PageIndex{2}\)

Colleges frequently provide estimates of student expenses such as housing. A consultant hired by a community college claimed that the average student housing expense was $650 per month. What are the null and alternative hypotheses to test whether this claim is accurate? 18

H A : The average cost is different than $650 per month, \(\mu \ne\) $650.

18 Applying the normal model requires that certain conditions are met. Because the data are a simple random sample and the sample (presumably) represents no more than 10% of all students at the college, the observations are independent. The sample size is also sufficiently large (n = 75) and the data exhibit only moderate skew. Thus, the normal model may be applied to the sample mean.

Exercise \(\PageIndex{3}\)

The community college decides to collect data to evaluate the $650 per month claim. They take a random sample of 75 students at their school and obtain the data represented in Figure 4.11. Can we apply the normal model to the sample mean?

If the court makes a Type 1 Error, this means the defendant is innocent (H 0 true) but wrongly convicted. A Type 2 Error means the court failed to reject H 0 (i.e. failed to convict the person) when she was in fact guilty (H A true).

Example \(\PageIndex{2}\)

The sample mean for student housing is $611.63 and the sample standard deviation is $132.85. Construct a 95% confidence interval for the population mean and evaluate the hypotheses of Exercise 4.22.

The standard error associated with the mean may be estimated using the sample standard deviation divided by the square root of the sample size. Recall that n = 75 students were sampled.

\[ SE = \dfrac {s}{\sqrt {n}} = \dfrac {132.85}{\sqrt {75}} = 15.34\]

You showed in Exercise 4.23 that the normal model may be applied to the sample mean. This ensures a 95% confidence interval may be accurately constructed:

\[\bar {x} \pm z*SE \rightarrow 611.63 \pm 1.96 \times 15.34 \times (581.56, 641.70)\]

Because the null value $650 is not in the confidence interval, a true mean of $650 is implausible and we reject the null hypothesis. The data provide statistically significant evidence that the actual average housing expense is less than $650 per month.

Decision Errors

Hypothesis tests are not flawless. Just think of the court system: innocent people are sometimes wrongly convicted and the guilty sometimes walk free. Similarly, we can make a wrong decision in statistical hypothesis tests. However, the difference is that we have the tools necessary to quantify how often we make such errors.

There are two competing hypotheses: the null and the alternative. In a hypothesis test, we make a statement about which one might be true, but we might choose incorrectly. There are four possible scenarios in a hypothesis test, which are summarized in Table 4.12.

A Type 1 Error is rejecting the null hypothesis when H0 is actually true. A Type 2 Error is failing to reject the null hypothesis when the alternative is actually true.

Exercise 4.25

In a US court, the defendant is either innocent (H 0 ) or guilty (H A ). What does a Type 1 Error represent in this context? What does a Type 2 Error represent? Table 4.12 may be useful.

To lower the Type 1 Error rate, we might raise our standard for conviction from "beyond a reasonable doubt" to "beyond a conceivable doubt" so fewer people would be wrongly convicted. However, this would also make it more difficult to convict the people who are actually guilty, so we would make more Type 2 Errors.

Exercise 4.26

How could we reduce the Type 1 Error rate in US courts? What influence would this have on the Type 2 Error rate?

To lower the Type 2 Error rate, we want to convict more guilty people. We could lower the standards for conviction from "beyond a reasonable doubt" to "beyond a little doubt". Lowering the bar for guilt will also result in more wrongful convictions, raising the Type 1 Error rate.

Exercise 4.27

How could we reduce the Type 2 Error rate in US courts? What influence would this have on the Type 1 Error rate?

A skeptic would have no reason to believe that sleep patterns at this school are different than the sleep patterns at another school.

Exercises 4.25-4.27 provide an important lesson:

If we reduce how often we make one type of error, we generally make more of the other type.

Hypothesis testing is built around rejecting or failing to reject the null hypothesis. That is, we do not reject H 0 unless we have strong evidence. But what precisely does strong evidence mean? As a general rule of thumb, for those cases where the null hypothesis is actually true, we do not want to incorrectly reject H 0 more than 5% of the time. This corresponds to a significance level of 0.05. We often write the significance level using \(\alpha\) (the Greek letter alpha): \(\alpha = 0.05.\) We discuss the appropriateness of different significance levels in Section 4.3.6.

If we use a 95% confidence interval to test a hypothesis where the null hypothesis is true, we will make an error whenever the point estimate is at least 1.96 standard errors away from the population parameter. This happens about 5% of the time (2.5% in each tail). Similarly, using a 99% con dence interval to evaluate a hypothesis is equivalent to a significance level of \(\alpha = 0.01\).

A confidence interval is, in one sense, simplistic in the world of hypothesis tests. Consider the following two scenarios:

• The null value (the parameter value under the null hypothesis) is in the 95% confidence interval but just barely, so we would not reject H 0 . However, we might like to somehow say, quantitatively, that it was a close decision.
• The null value is very far outside of the interval, so we reject H 0 . However, we want to communicate that, not only did we reject the null hypothesis, but it wasn't even close. Such a case is depicted in Figure 4.13.

In Section 4.3.4, we introduce a tool called the p-value that will be helpful in these cases. The p-value method also extends to hypothesis tests where con dence intervals cannot be easily constructed or applied.

Formal Testing using p-Values

The p-value is a way of quantifying the strength of the evidence against the null hypothesis and in favor of the alternative. Formally the p-value is a conditional probability.

definition: p-value

The p-value is the probability of observing data at least as favorable to the alternative hypothesis as our current data set, if the null hypothesis is true. We typically use a summary statistic of the data, in this chapter the sample mean, to help compute the p-value and evaluate the hypotheses.

A poll by the National Sleep Foundation found that college students average about 7 hours of sleep per night. Researchers at a rural school are interested in showing that students at their school sleep longer than seven hours on average, and they would like to demonstrate this using a sample of students. What would be an appropriate skeptical position for this research?

This is entirely based on the interests of the researchers. Had they been only interested in the opposite case - showing that their students were actually averaging fewer than seven hours of sleep but not interested in showing more than 7 hours - then our setup would have set the alternative as \(\mu < 7\).

We can set up the null hypothesis for this test as a skeptical perspective: the students at this school average 7 hours of sleep per night. The alternative hypothesis takes a new form reflecting the interests of the research: the students average more than 7 hours of sleep. We can write these hypotheses as

• H 0 : \(\mu\) = 7.
• H A : \(\mu\) > 7.

Using \(\mu\) > 7 as the alternative is an example of a one-sided hypothesis test. In this investigation, there is no apparent interest in learning whether the mean is less than 7 hours. (The standard error can be estimated from the sample standard deviation and the sample size: \(SE_{\bar {x}} = \dfrac {s_x}{\sqrt {n}} = \dfrac {1.75}{\sqrt {110}} = 0.17\)). Earlier we encountered a two-sided hypothesis where we looked for any clear difference, greater than or less than the null value.

Always use a two-sided test unless it was made clear prior to data collection that the test should be one-sided. Switching a two-sided test to a one-sided test after observing the data is dangerous because it can inflate the Type 1 Error rate.

TIP: One-sided and two-sided tests

If the researchers are only interested in showing an increase or a decrease, but not both, use a one-sided test. If the researchers would be interested in any difference from the null value - an increase or decrease - then the test should be two-sided.

TIP: Always write the null hypothesis as an equality

We will find it most useful if we always list the null hypothesis as an equality (e.g. \(\mu\) = 7) while the alternative always uses an inequality (e.g. \(\mu \ne 7, \mu > 7, or \mu < 7)\).

The researchers at the rural school conducted a simple random sample of n = 110 students on campus. They found that these students averaged 7.42 hours of sleep and the standard deviation of the amount of sleep for the students was 1.75 hours. A histogram of the sample is shown in Figure 4.14.

Before we can use a normal model for the sample mean or compute the standard error of the sample mean, we must verify conditions. (1) Because this is a simple random sample from less than 10% of the student body, the observations are independent. (2) The sample size in the sleep study is sufficiently large since it is greater than 30. (3) The data show moderate skew in Figure 4.14 and the presence of a couple of outliers. This skew and the outliers (which are not too extreme) are acceptable for a sample size of n = 110. With these conditions veri ed, the normal model can be safely applied to \(\bar {x}\) and the estimated standard error will be very accurate.

What is the standard deviation associated with \(\bar {x}\)? That is, estimate the standard error of \(\bar {x}\). 25

The hypothesis test will be evaluated using a significance level of \(\alpha = 0.05\). We want to consider the data under the scenario that the null hypothesis is true. In this case, the sample mean is from a distribution that is nearly normal and has mean 7 and standard deviation of about 0.17. Such a distribution is shown in Figure 4.15.

The shaded tail in Figure 4.15 represents the chance of observing such a large mean, conditional on the null hypothesis being true. That is, the shaded tail represents the p-value. We shade all means larger than our sample mean, \(\bar {x} = 7.42\), because they are more favorable to the alternative hypothesis than the observed mean.

We compute the p-value by finding the tail area of this normal distribution, which we learned to do in Section 3.1. First compute the Z score of the sample mean, \(\bar {x} = 7.42\):

\[Z = \dfrac {\bar {x} - \text {null value}}{SE_{\bar {x}}} = \dfrac {7.42 - 7}{0.17} = 2.47\]

Using the normal probability table, the lower unshaded area is found to be 0.993. Thus the shaded area is 1 - 0.993 = 0.007. If the null hypothesis is true, the probability of observing such a large sample mean for a sample of 110 students is only 0.007. That is, if the null hypothesis is true, we would not often see such a large mean.

We evaluate the hypotheses by comparing the p-value to the significance level. Because the p-value is less than the significance level \((p-value = 0.007 < 0.05 = \alpha)\), we reject the null hypothesis. What we observed is so unusual with respect to the null hypothesis that it casts serious doubt on H 0 and provides strong evidence favoring H A .

p-value as a tool in hypothesis testing

The p-value quantifies how strongly the data favor H A over H 0 . A small p-value (usually < 0.05) corresponds to sufficient evidence to reject H 0 in favor of H A .

TIP: It is useful to First draw a picture to find the p-value

It is useful to draw a picture of the distribution of \(\bar {x}\) as though H 0 was true (i.e. \(\mu\) equals the null value), and shade the region (or regions) of sample means that are at least as favorable to the alternative hypothesis. These shaded regions represent the p-value.

The ideas below review the process of evaluating hypothesis tests with p-values:

• The null hypothesis represents a skeptic's position or a position of no difference. We reject this position only if the evidence strongly favors H A .
• A small p-value means that if the null hypothesis is true, there is a low probability of seeing a point estimate at least as extreme as the one we saw. We interpret this as strong evidence in favor of the alternative.
• We reject the null hypothesis if the p-value is smaller than the significance level, \(\alpha\), which is usually 0.05. Otherwise, we fail to reject H 0 .
• We should always state the conclusion of the hypothesis test in plain language so non-statisticians can also understand the results.

The p-value is constructed in such a way that we can directly compare it to the significance level ( \(\alpha\)) to determine whether or not to reject H 0 . This method ensures that the Type 1 Error rate does not exceed the significance level standard.

If the null hypothesis is true, how often should the p-value be less than 0.05?

About 5% of the time. If the null hypothesis is true, then the data only has a 5% chance of being in the 5% of data most favorable to H A .

Exercise 4.31

Suppose we had used a significance level of 0.01 in the sleep study. Would the evidence have been strong enough to reject the null hypothesis? (The p-value was 0.007.) What if the significance level was \(\alpha = 0.001\)? 27

27 We reject the null hypothesis whenever p-value < \(\alpha\). Thus, we would still reject the null hypothesis if \(\alpha = 0.01\) but not if the significance level had been \(\alpha = 0.001\).

Exercise 4.32

Ebay might be interested in showing that buyers on its site tend to pay less than they would for the corresponding new item on Amazon. We'll research this topic for one particular product: a video game called Mario Kart for the Nintendo Wii. During early October 2009, Amazon sold this game for $46.99. Set up an appropriate (one-sided!) hypothesis test to check the claim that Ebay buyers pay less during auctions at this same time. 28

28 The skeptic would say the average is the same on Ebay, and we are interested in showing the average price is lower.

Exercise 4.33

During early October, 2009, 52 Ebay auctions were recorded for Mario Kart.29 The total prices for the auctions are presented using a histogram in Figure 4.17, and we may like to apply the normal model to the sample mean. Check the three conditions required for applying the normal model: (1) independence, (2) at least 30 observations, and (3) the data are not strongly skewed. 30

30 (1) The independence condition is unclear. We will make the assumption that the observations are independent, which we should report with any nal results. (2) The sample size is sufficiently large: \(n = 52 \ge 30\). (3) The data distribution is not strongly skewed; it is approximately symmetric.

H 0 : The average auction price on Ebay is equal to (or more than) the price on Amazon. We write only the equality in the statistical notation: \(\mu_{ebay} = 46.99\).

H A : The average price on Ebay is less than the price on Amazon, \(\mu _{ebay} < 46.99\).

29 These data were collected by OpenIntro staff.

Example 4.34

The average sale price of the 52 Ebay auctions for Wii Mario Kart was $44.17 with a standard deviation of $4.15. Does this provide sufficient evidence to reject the null hypothesis in Exercise 4.32? Use a significance level of \(\alpha = 0.01\).

The hypotheses were set up and the conditions were checked in Exercises 4.32 and 4.33. The next step is to find the standard error of the sample mean and produce a sketch to help find the p-value.

Because the alternative hypothesis says we are looking for a smaller mean, we shade the lower tail. We find this shaded area by using the Z score and normal probability table: \(Z = \dfrac {44.17 \times 46.99}{0.5755} = -4.90\), which has area less than 0.0002. The area is so small we cannot really see it on the picture. This lower tail area corresponds to the p-value.

Because the p-value is so small - specifically, smaller than = 0.01 - this provides sufficiently strong evidence to reject the null hypothesis in favor of the alternative. The data provide statistically signi cant evidence that the average price on Ebay is lower than Amazon's asking price.

Two-sided hypothesis testing with p-values

We now consider how to compute a p-value for a two-sided test. In one-sided tests, we shade the single tail in the direction of the alternative hypothesis. For example, when the alternative had the form \(\mu\) > 7, then the p-value was represented by the upper tail (Figure 4.16). When the alternative was \(\mu\) < 46.99, the p-value was the lower tail (Exercise 4.32). In a two-sided test, we shade two tails since evidence in either direction is favorable to H A .

Exercise 4.35 Earlier we talked about a research group investigating whether the students at their school slept longer than 7 hours each night. Let's consider a second group of researchers who want to evaluate whether the students at their college differ from the norm of 7 hours. Write the null and alternative hypotheses for this investigation. 31

Example 4.36 The second college randomly samples 72 students and nds a mean of \(\bar {x} = 6.83\) hours and a standard deviation of s = 1.8 hours. Does this provide strong evidence against H 0 in Exercise 4.35? Use a significance level of \(\alpha = 0.05\).

First, we must verify assumptions. (1) A simple random sample of less than 10% of the student body means the observations are independent. (2) The sample size is 72, which is greater than 30. (3) Based on the earlier distribution and what we already know about college student sleep habits, the distribution is probably not strongly skewed.

Next we can compute the standard error \((SE_{\bar {x}} = \dfrac {s}{\sqrt {n}} = 0.21)\) of the estimate and create a picture to represent the p-value, shown in Figure 4.18. Both tails are shaded.

31 Because the researchers are interested in any difference, they should use a two-sided setup: H 0 : \(\mu\) = 7, H A : \(\mu \ne 7.\)

An estimate of 7.17 or more provides at least as strong of evidence against the null hypothesis and in favor of the alternative as the observed estimate, \(\bar {x} = 6.83\).

We can calculate the tail areas by rst nding the lower tail corresponding to \(\bar {x}\):

\[Z = \dfrac {6.83 - 7.00}{0.21} = -0.81 \xrightarrow {table} \text {left tail} = 0.2090\]

Because the normal model is symmetric, the right tail will have the same area as the left tail. The p-value is found as the sum of the two shaded tails:

\[ \text {p-value} = \text {left tail} + \text {right tail} = 2 \times \text {(left tail)} = 0.4180\]

This p-value is relatively large (larger than \(\mu\)= 0.05), so we should not reject H 0 . That is, if H 0 is true, it would not be very unusual to see a sample mean this far from 7 hours simply due to sampling variation. Thus, we do not have sufficient evidence to conclude that the mean is different than 7 hours.

Example 4.37 It is never okay to change two-sided tests to one-sided tests after observing the data. In this example we explore the consequences of ignoring this advice. Using \(\alpha = 0.05\), we show that freely switching from two-sided tests to onesided tests will cause us to make twice as many Type 1 Errors as intended.

Suppose the sample mean was larger than the null value, \(\mu_0\) (e.g. \(\mu_0\) would represent 7 if H 0 : \(\mu\) = 7). Then if we can ip to a one-sided test, we would use H A : \(\mu > \mu_0\). Now if we obtain any observation with a Z score greater than 1.65, we would reject H 0 . If the null hypothesis is true, we incorrectly reject the null hypothesis about 5% of the time when the sample mean is above the null value, as shown in Figure 4.19.

Suppose the sample mean was smaller than the null value. Then if we change to a one-sided test, we would use H A : \(\mu < \mu_0\). If \(\bar {x}\) had a Z score smaller than -1.65, we would reject H 0 . If the null hypothesis is true, then we would observe such a case about 5% of the time.

By examining these two scenarios, we can determine that we will make a Type 1 Error 5% + 5% = 10% of the time if we are allowed to swap to the "best" one-sided test for the data. This is twice the error rate we prescribed with our significance level: \(\alpha = 0.05\) (!).

Caution: One-sided hypotheses are allowed only before seeing data

After observing data, it is tempting to turn a two-sided test into a one-sided test. Avoid this temptation. Hypotheses must be set up before observing the data. If they are not, the test must be two-sided.

Choosing a Significance Level

Choosing a significance level for a test is important in many contexts, and the traditional level is 0.05. However, it is often helpful to adjust the significance level based on the application. We may select a level that is smaller or larger than 0.05 depending on the consequences of any conclusions reached from the test.

• If making a Type 1 Error is dangerous or especially costly, we should choose a small significance level (e.g. 0.01). Under this scenario we want to be very cautious about rejecting the null hypothesis, so we demand very strong evidence favoring H A before we would reject H 0 .
• If a Type 2 Error is relatively more dangerous or much more costly than a Type 1 Error, then we should choose a higher significance level (e.g. 0.10). Here we want to be cautious about failing to reject H 0 when the null is actually false. We will discuss this particular case in greater detail in Section 4.6.

Significance levels should reflect consequences of errors

The significance level selected for a test should reflect the consequences associated with Type 1 and Type 2 Errors.

Example 4.38

A car manufacturer is considering a higher quality but more expensive supplier for window parts in its vehicles. They sample a number of parts from their current supplier and also parts from the new supplier. They decide that if the high quality parts will last more than 12% longer, it makes nancial sense to switch to this more expensive supplier. Is there good reason to modify the significance level in such a hypothesis test?

The null hypothesis is that the more expensive parts last no more than 12% longer while the alternative is that they do last more than 12% longer. This decision is just one of the many regular factors that have a marginal impact on the car and company. A significancelevel of 0.05 seems reasonable since neither a Type 1 or Type 2 error should be dangerous or (relatively) much more expensive.

Example 4.39

The same car manufacturer is considering a slightly more expensive supplier for parts related to safety, not windows. If the durability of these safety components is shown to be better than the current supplier, they will switch manufacturers. Is there good reason to modify the significance level in such an evaluation?

The null hypothesis would be that the suppliers' parts are equally reliable. Because safety is involved, the car company should be eager to switch to the slightly more expensive manufacturer (reject H 0 ) even if the evidence of increased safety is only moderately strong. A slightly larger significance level, such as \(\mu = 0.10\), might be appropriate.

Exercise 4.40

A part inside of a machine is very expensive to replace. However, the machine usually functions properly even if this part is broken, so the part is replaced only if we are extremely certain it is broken based on a series of measurements. Identify appropriate hypotheses for this test (in plain language) and suggest an appropriate significance level. 32

If you're seeing this message, it means we're having trouble loading external resources on our website.

If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.

To log in and use all the features of Khan Academy, please enable JavaScript in your browser.

Unit 12: Significance tests (hypothesis testing)

About this unit, the idea of significance tests.

• Simple hypothesis testing (Opens a modal)
• Idea behind hypothesis testing (Opens a modal)
• Examples of null and alternative hypotheses (Opens a modal)
• P-values and significance tests (Opens a modal)
• Comparing P-values to different significance levels (Opens a modal)
• Estimating a P-value from a simulation (Opens a modal)
• Using P-values to make conclusions (Opens a modal)
• Simple hypothesis testing Get 3 of 4 questions to level up!
• Writing null and alternative hypotheses Get 3 of 4 questions to level up!
• Estimating P-values from simulations Get 3 of 4 questions to level up!

Error probabilities and power

• Introduction to Type I and Type II errors (Opens a modal)
• Type 1 errors (Opens a modal)
• Examples identifying Type I and Type II errors (Opens a modal)
• Introduction to power in significance tests (Opens a modal)
• Examples thinking about power in significance tests (Opens a modal)
• Consequences of errors and significance (Opens a modal)
• Type I vs Type II error Get 3 of 4 questions to level up!
• Error probabilities and power Get 3 of 4 questions to level up!

Tests about a population proportion

• Constructing hypotheses for a significance test about a proportion (Opens a modal)
• Conditions for a z test about a proportion (Opens a modal)
• Reference: Conditions for inference on a proportion (Opens a modal)
• Calculating a z statistic in a test about a proportion (Opens a modal)
• Calculating a P-value given a z statistic (Opens a modal)
• Making conclusions in a test about a proportion (Opens a modal)
• Writing hypotheses for a test about a proportion Get 3 of 4 questions to level up!
• Conditions for a z test about a proportion Get 3 of 4 questions to level up!
• Calculating the test statistic in a z test for a proportion Get 3 of 4 questions to level up!
• Calculating the P-value in a z test for a proportion Get 3 of 4 questions to level up!
• Making conclusions in a z test for a proportion Get 3 of 4 questions to level up!

Tests about a population mean

• Writing hypotheses for a significance test about a mean (Opens a modal)
• Conditions for a t test about a mean (Opens a modal)
• Reference: Conditions for inference on a mean (Opens a modal)
• When to use z or t statistics in significance tests (Opens a modal)
• Example calculating t statistic for a test about a mean (Opens a modal)
• Using TI calculator for P-value from t statistic (Opens a modal)
• Using a table to estimate P-value from t statistic (Opens a modal)
• Comparing P-value from t statistic to significance level (Opens a modal)
• Free response example: Significance test for a mean (Opens a modal)
• Writing hypotheses for a test about a mean Get 3 of 4 questions to level up!
• Conditions for a t test about a mean Get 3 of 4 questions to level up!
• Calculating the test statistic in a t test for a mean Get 3 of 4 questions to level up!
• Calculating the P-value in a t test for a mean Get 3 of 4 questions to level up!
• Making conclusions in a t test for a mean Get 3 of 4 questions to level up!

More significance testing videos

• Hypothesis testing and p-values (Opens a modal)
• One-tailed and two-tailed tests (Opens a modal)
• Z-statistics vs. T-statistics (Opens a modal)
• Small sample hypothesis test (Opens a modal)
• Large sample proportion hypothesis testing (Opens a modal)

Hypothesis Testing

Hypothesis testing is a tool for making statistical inferences about the population data. It is an analysis tool that tests assumptions and determines how likely something is within a given standard of accuracy. Hypothesis testing provides a way to verify whether the results of an experiment are valid.

A null hypothesis and an alternative hypothesis are set up before performing the hypothesis testing. This helps to arrive at a conclusion regarding the sample obtained from the population. In this article, we will learn more about hypothesis testing, its types, steps to perform the testing, and associated examples.

What is Hypothesis Testing in Statistics?

Hypothesis testing uses sample data from the population to draw useful conclusions regarding the population probability distribution . It tests an assumption made about the data using different types of hypothesis testing methodologies. The hypothesis testing results in either rejecting or not rejecting the null hypothesis.

Hypothesis Testing Definition

Hypothesis testing can be defined as a statistical tool that is used to identify if the results of an experiment are meaningful or not. It involves setting up a null hypothesis and an alternative hypothesis. These two hypotheses will always be mutually exclusive. This means that if the null hypothesis is true then the alternative hypothesis is false and vice versa. An example of hypothesis testing is setting up a test to check if a new medicine works on a disease in a more efficient manner.

Null Hypothesis

The null hypothesis is a concise mathematical statement that is used to indicate that there is no difference between two possibilities. In other words, there is no difference between certain characteristics of data. This hypothesis assumes that the outcomes of an experiment are based on chance alone. It is denoted as \(H_{0}\). Hypothesis testing is used to conclude if the null hypothesis can be rejected or not. Suppose an experiment is conducted to check if girls are shorter than boys at the age of 5. The null hypothesis will say that they are the same height.

Alternative Hypothesis

The alternative hypothesis is an alternative to the null hypothesis. It is used to show that the observations of an experiment are due to some real effect. It indicates that there is a statistical significance between two possible outcomes and can be denoted as \(H_{1}\) or \(H_{a}\). For the above-mentioned example, the alternative hypothesis would be that girls are shorter than boys at the age of 5.

Hypothesis Testing P Value

In hypothesis testing, the p value is used to indicate whether the results obtained after conducting a test are statistically significant or not. It also indicates the probability of making an error in rejecting or not rejecting the null hypothesis.This value is always a number between 0 and 1. The p value is compared to an alpha level, \(\alpha\) or significance level. The alpha level can be defined as the acceptable risk of incorrectly rejecting the null hypothesis. The alpha level is usually chosen between 1% to 5%.

Hypothesis Testing Critical region

All sets of values that lead to rejecting the null hypothesis lie in the critical region. Furthermore, the value that separates the critical region from the non-critical region is known as the critical value.

Hypothesis Testing Formula

Depending upon the type of data available and the size, different types of hypothesis testing are used to determine whether the null hypothesis can be rejected or not. The hypothesis testing formula for some important test statistics are given below:

• z = \(\frac{\overline{x}-\mu}{\frac{\sigma}{\sqrt{n}}}\). \(\overline{x}\) is the sample mean, \(\mu\) is the population mean, \(\sigma\) is the population standard deviation and n is the size of the sample.
• t = \(\frac{\overline{x}-\mu}{\frac{s}{\sqrt{n}}}\). s is the sample standard deviation.
• \(\chi ^{2} = \sum \frac{(O_{i}-E_{i})^{2}}{E_{i}}\). \(O_{i}\) is the observed value and \(E_{i}\) is the expected value.

We will learn more about these test statistics in the upcoming section.

Types of Hypothesis Testing

Selecting the correct test for performing hypothesis testing can be confusing. These tests are used to determine a test statistic on the basis of which the null hypothesis can either be rejected or not rejected. Some of the important tests used for hypothesis testing are given below.

Hypothesis Testing Z Test

A z test is a way of hypothesis testing that is used for a large sample size (n ≥ 30). It is used to determine whether there is a difference between the population mean and the sample mean when the population standard deviation is known. It can also be used to compare the mean of two samples. It is used to compute the z test statistic. The formulas are given as follows:

• One sample: z = \(\frac{\overline{x}-\mu}{\frac{\sigma}{\sqrt{n}}}\).
• Two samples: z = \(\frac{(\overline{x_{1}}-\overline{x_{2}})-(\mu_{1}-\mu_{2})}{\sqrt{\frac{\sigma_{1}^{2}}{n_{1}}+\frac{\sigma_{2}^{2}}{n_{2}}}}\).

Hypothesis Testing t Test

The t test is another method of hypothesis testing that is used for a small sample size (n < 30). It is also used to compare the sample mean and population mean. However, the population standard deviation is not known. Instead, the sample standard deviation is known. The mean of two samples can also be compared using the t test.

• One sample: t = \(\frac{\overline{x}-\mu}{\frac{s}{\sqrt{n}}}\).
• Two samples: t = \(\frac{(\overline{x_{1}}-\overline{x_{2}})-(\mu_{1}-\mu_{2})}{\sqrt{\frac{s_{1}^{2}}{n_{1}}+\frac{s_{2}^{2}}{n_{2}}}}\).

Hypothesis Testing Chi Square

The Chi square test is a hypothesis testing method that is used to check whether the variables in a population are independent or not. It is used when the test statistic is chi-squared distributed.

One Tailed Hypothesis Testing

One tailed hypothesis testing is done when the rejection region is only in one direction. It can also be known as directional hypothesis testing because the effects can be tested in one direction only. This type of testing is further classified into the right tailed test and left tailed test.

Right Tailed Hypothesis Testing

The right tail test is also known as the upper tail test. This test is used to check whether the population parameter is greater than some value. The null and alternative hypotheses for this test are given as follows:

\(H_{0}\): The population parameter is ≤ some value

\(H_{1}\): The population parameter is > some value.

If the test statistic has a greater value than the critical value then the null hypothesis is rejected

Left Tailed Hypothesis Testing

The left tail test is also known as the lower tail test. It is used to check whether the population parameter is less than some value. The hypotheses for this hypothesis testing can be written as follows:

\(H_{0}\): The population parameter is ≥ some value

\(H_{1}\): The population parameter is < some value.

The null hypothesis is rejected if the test statistic has a value lesser than the critical value.

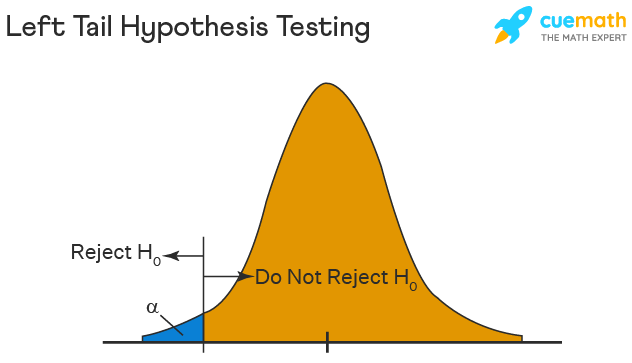
Two Tailed Hypothesis Testing

In this hypothesis testing method, the critical region lies on both sides of the sampling distribution. It is also known as a non - directional hypothesis testing method. The two-tailed test is used when it needs to be determined if the population parameter is assumed to be different than some value. The hypotheses can be set up as follows:

\(H_{0}\): the population parameter = some value

\(H_{1}\): the population parameter ≠ some value

The null hypothesis is rejected if the test statistic has a value that is not equal to the critical value.

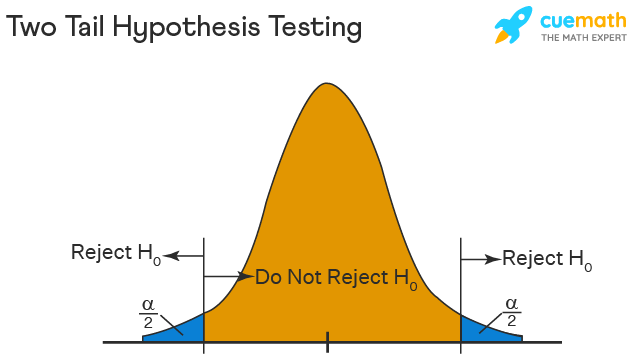
Hypothesis Testing Steps

Hypothesis testing can be easily performed in five simple steps. The most important step is to correctly set up the hypotheses and identify the right method for hypothesis testing. The basic steps to perform hypothesis testing are as follows:

• Step 1: Set up the null hypothesis by correctly identifying whether it is the left-tailed, right-tailed, or two-tailed hypothesis testing.
• Step 2: Set up the alternative hypothesis.
• Step 3: Choose the correct significance level, \(\alpha\), and find the critical value.
• Step 4: Calculate the correct test statistic (z, t or \(\chi\)) and p-value.
• Step 5: Compare the test statistic with the critical value or compare the p-value with \(\alpha\) to arrive at a conclusion. In other words, decide if the null hypothesis is to be rejected or not.

Hypothesis Testing Example

The best way to solve a problem on hypothesis testing is by applying the 5 steps mentioned in the previous section. Suppose a researcher claims that the mean average weight of men is greater than 100kgs with a standard deviation of 15kgs. 30 men are chosen with an average weight of 112.5 Kgs. Using hypothesis testing, check if there is enough evidence to support the researcher's claim. The confidence interval is given as 95%.

Step 1: This is an example of a right-tailed test. Set up the null hypothesis as \(H_{0}\): \(\mu\) = 100.

Step 2: The alternative hypothesis is given by \(H_{1}\): \(\mu\) > 100.

Step 3: As this is a one-tailed test, \(\alpha\) = 100% - 95% = 5%. This can be used to determine the critical value.

1 - \(\alpha\) = 1 - 0.05 = 0.95

0.95 gives the required area under the curve. Now using a normal distribution table, the area 0.95 is at z = 1.645. A similar process can be followed for a t-test. The only additional requirement is to calculate the degrees of freedom given by n - 1.

Step 4: Calculate the z test statistic. This is because the sample size is 30. Furthermore, the sample and population means are known along with the standard deviation.

z = \(\frac{\overline{x}-\mu}{\frac{\sigma}{\sqrt{n}}}\).

\(\mu\) = 100, \(\overline{x}\) = 112.5, n = 30, \(\sigma\) = 15

z = \(\frac{112.5-100}{\frac{15}{\sqrt{30}}}\) = 4.56

Step 5: Conclusion. As 4.56 > 1.645 thus, the null hypothesis can be rejected.

Hypothesis Testing and Confidence Intervals

Confidence intervals form an important part of hypothesis testing. This is because the alpha level can be determined from a given confidence interval. Suppose a confidence interval is given as 95%. Subtract the confidence interval from 100%. This gives 100 - 95 = 5% or 0.05. This is the alpha value of a one-tailed hypothesis testing. To obtain the alpha value for a two-tailed hypothesis testing, divide this value by 2. This gives 0.05 / 2 = 0.025.

Related Articles:

• Probability and Statistics
• Data Handling

Important Notes on Hypothesis Testing

• Hypothesis testing is a technique that is used to verify whether the results of an experiment are statistically significant.
• It involves the setting up of a null hypothesis and an alternate hypothesis.
• There are three types of tests that can be conducted under hypothesis testing - z test, t test, and chi square test.
• Hypothesis testing can be classified as right tail, left tail, and two tail tests.

Examples on Hypothesis Testing

• Example 1: The average weight of a dumbbell in a gym is 90lbs. However, a physical trainer believes that the average weight might be higher. A random sample of 5 dumbbells with an average weight of 110lbs and a standard deviation of 18lbs. Using hypothesis testing check if the physical trainer's claim can be supported for a 95% confidence level. Solution: As the sample size is lesser than 30, the t-test is used. \(H_{0}\): \(\mu\) = 90, \(H_{1}\): \(\mu\) > 90 \(\overline{x}\) = 110, \(\mu\) = 90, n = 5, s = 18. \(\alpha\) = 0.05 Using the t-distribution table, the critical value is 2.132 t = \(\frac{\overline{x}-\mu}{\frac{s}{\sqrt{n}}}\) t = 2.484 As 2.484 > 2.132, the null hypothesis is rejected. Answer: The average weight of the dumbbells may be greater than 90lbs
• Example 2: The average score on a test is 80 with a standard deviation of 10. With a new teaching curriculum introduced it is believed that this score will change. On random testing, the score of 38 students, the mean was found to be 88. With a 0.05 significance level, is there any evidence to support this claim? Solution: This is an example of two-tail hypothesis testing. The z test will be used. \(H_{0}\): \(\mu\) = 80, \(H_{1}\): \(\mu\) ≠ 80 \(\overline{x}\) = 88, \(\mu\) = 80, n = 36, \(\sigma\) = 10. \(\alpha\) = 0.05 / 2 = 0.025 The critical value using the normal distribution table is 1.96 z = \(\frac{\overline{x}-\mu}{\frac{\sigma}{\sqrt{n}}}\) z = \(\frac{88-80}{\frac{10}{\sqrt{36}}}\) = 4.8 As 4.8 > 1.96, the null hypothesis is rejected. Answer: There is a difference in the scores after the new curriculum was introduced.
• Example 3: The average score of a class is 90. However, a teacher believes that the average score might be lower. The scores of 6 students were randomly measured. The mean was 82 with a standard deviation of 18. With a 0.05 significance level use hypothesis testing to check if this claim is true. Solution: The t test will be used. \(H_{0}\): \(\mu\) = 90, \(H_{1}\): \(\mu\) < 90 \(\overline{x}\) = 110, \(\mu\) = 90, n = 6, s = 18 The critical value from the t table is -2.015 t = \(\frac{\overline{x}-\mu}{\frac{s}{\sqrt{n}}}\) t = \(\frac{82-90}{\frac{18}{\sqrt{6}}}\) t = -1.088 As -1.088 > -2.015, we fail to reject the null hypothesis. Answer: There is not enough evidence to support the claim.

go to slide go to slide go to slide

Book a Free Trial Class

FAQs on Hypothesis Testing

What is hypothesis testing.

Hypothesis testing in statistics is a tool that is used to make inferences about the population data. It is also used to check if the results of an experiment are valid.

What is the z Test in Hypothesis Testing?

The z test in hypothesis testing is used to find the z test statistic for normally distributed data . The z test is used when the standard deviation of the population is known and the sample size is greater than or equal to 30.

What is the t Test in Hypothesis Testing?

The t test in hypothesis testing is used when the data follows a student t distribution . It is used when the sample size is less than 30 and standard deviation of the population is not known.

What is the formula for z test in Hypothesis Testing?

The formula for a one sample z test in hypothesis testing is z = \(\frac{\overline{x}-\mu}{\frac{\sigma}{\sqrt{n}}}\) and for two samples is z = \(\frac{(\overline{x_{1}}-\overline{x_{2}})-(\mu_{1}-\mu_{2})}{\sqrt{\frac{\sigma_{1}^{2}}{n_{1}}+\frac{\sigma_{2}^{2}}{n_{2}}}}\).

What is the p Value in Hypothesis Testing?

The p value helps to determine if the test results are statistically significant or not. In hypothesis testing, the null hypothesis can either be rejected or not rejected based on the comparison between the p value and the alpha level.

What is One Tail Hypothesis Testing?

When the rejection region is only on one side of the distribution curve then it is known as one tail hypothesis testing. The right tail test and the left tail test are two types of directional hypothesis testing.

What is the Alpha Level in Two Tail Hypothesis Testing?

To get the alpha level in a two tail hypothesis testing divide \(\alpha\) by 2. This is done as there are two rejection regions in the curve.

User Preferences

Content preview.

Arcu felis bibendum ut tristique et egestas quis:

• Ut enim ad minim veniam, quis nostrud exercitation ullamco laboris
• Duis aute irure dolor in reprehenderit in voluptate
• Excepteur sint occaecat cupidatat non proident

Keyboard Shortcuts

S.3.2 hypothesis testing (p-value approach).

The P -value approach involves determining "likely" or "unlikely" by determining the probability — assuming the null hypothesis was true — of observing a more extreme test statistic in the direction of the alternative hypothesis than the one observed. If the P -value is small, say less than (or equal to) \(\alpha\), then it is "unlikely." And, if the P -value is large, say more than \(\alpha\), then it is "likely."

If the P -value is less than (or equal to) \(\alpha\), then the null hypothesis is rejected in favor of the alternative hypothesis. And, if the P -value is greater than \(\alpha\), then the null hypothesis is not rejected.

Specifically, the four steps involved in using the P -value approach to conducting any hypothesis test are:

• Specify the null and alternative hypotheses.
• Using the sample data and assuming the null hypothesis is true, calculate the value of the test statistic. Again, to conduct the hypothesis test for the population mean μ , we use the t -statistic \(t^*=\frac{\bar{x}-\mu}{s/\sqrt{n}}\) which follows a t -distribution with n - 1 degrees of freedom.
• Using the known distribution of the test statistic, calculate the P -value : "If the null hypothesis is true, what is the probability that we'd observe a more extreme test statistic in the direction of the alternative hypothesis than we did?" (Note how this question is equivalent to the question answered in criminal trials: "If the defendant is innocent, what is the chance that we'd observe such extreme criminal evidence?")
• Set the significance level, \(\alpha\), the probability of making a Type I error to be small — 0.01, 0.05, or 0.10. Compare the P -value to \(\alpha\). If the P -value is less than (or equal to) \(\alpha\), reject the null hypothesis in favor of the alternative hypothesis. If the P -value is greater than \(\alpha\), do not reject the null hypothesis.

Example S.3.2.1

Mean gpa section  .

In our example concerning the mean grade point average, suppose that our random sample of n = 15 students majoring in mathematics yields a test statistic t * equaling 2.5. Since n = 15, our test statistic t * has n - 1 = 14 degrees of freedom. Also, suppose we set our significance level α at 0.05 so that we have only a 5% chance of making a Type I error.

Right Tailed

The P -value for conducting the right-tailed test H 0 : μ = 3 versus H A : μ > 3 is the probability that we would observe a test statistic greater than t * = 2.5 if the population mean \(\mu\) really were 3. Recall that probability equals the area under the probability curve. The P -value is therefore the area under a t n - 1 = t 14 curve and to the right of the test statistic t * = 2.5. It can be shown using statistical software that the P -value is 0.0127. The graph depicts this visually.

The P -value, 0.0127, tells us it is "unlikely" that we would observe such an extreme test statistic t * in the direction of H A if the null hypothesis were true. Therefore, our initial assumption that the null hypothesis is true must be incorrect. That is, since the P -value, 0.0127, is less than \(\alpha\) = 0.05, we reject the null hypothesis H 0 : μ = 3 in favor of the alternative hypothesis H A : μ > 3.

Note that we would not reject H 0 : μ = 3 in favor of H A : μ > 3 if we lowered our willingness to make a Type I error to \(\alpha\) = 0.01 instead, as the P -value, 0.0127, is then greater than \(\alpha\) = 0.01.

Left Tailed

In our example concerning the mean grade point average, suppose that our random sample of n = 15 students majoring in mathematics yields a test statistic t * instead of equaling -2.5. The P -value for conducting the left-tailed test H 0 : μ = 3 versus H A : μ < 3 is the probability that we would observe a test statistic less than t * = -2.5 if the population mean μ really were 3. The P -value is therefore the area under a t n - 1 = t 14 curve and to the left of the test statistic t* = -2.5. It can be shown using statistical software that the P -value is 0.0127. The graph depicts this visually.

The P -value, 0.0127, tells us it is "unlikely" that we would observe such an extreme test statistic t * in the direction of H A if the null hypothesis were true. Therefore, our initial assumption that the null hypothesis is true must be incorrect. That is, since the P -value, 0.0127, is less than α = 0.05, we reject the null hypothesis H 0 : μ = 3 in favor of the alternative hypothesis H A : μ < 3.

Note that we would not reject H 0 : μ = 3 in favor of H A : μ < 3 if we lowered our willingness to make a Type I error to α = 0.01 instead, as the P -value, 0.0127, is then greater than \(\alpha\) = 0.01.

In our example concerning the mean grade point average, suppose again that our random sample of n = 15 students majoring in mathematics yields a test statistic t * instead of equaling -2.5. The P -value for conducting the two-tailed test H 0 : μ = 3 versus H A : μ ≠ 3 is the probability that we would observe a test statistic less than -2.5 or greater than 2.5 if the population mean μ really was 3. That is, the two-tailed test requires taking into account the possibility that the test statistic could fall into either tail (hence the name "two-tailed" test). The P -value is, therefore, the area under a t n - 1 = t 14 curve to the left of -2.5 and to the right of 2.5. It can be shown using statistical software that the P -value is 0.0127 + 0.0127, or 0.0254. The graph depicts this visually.

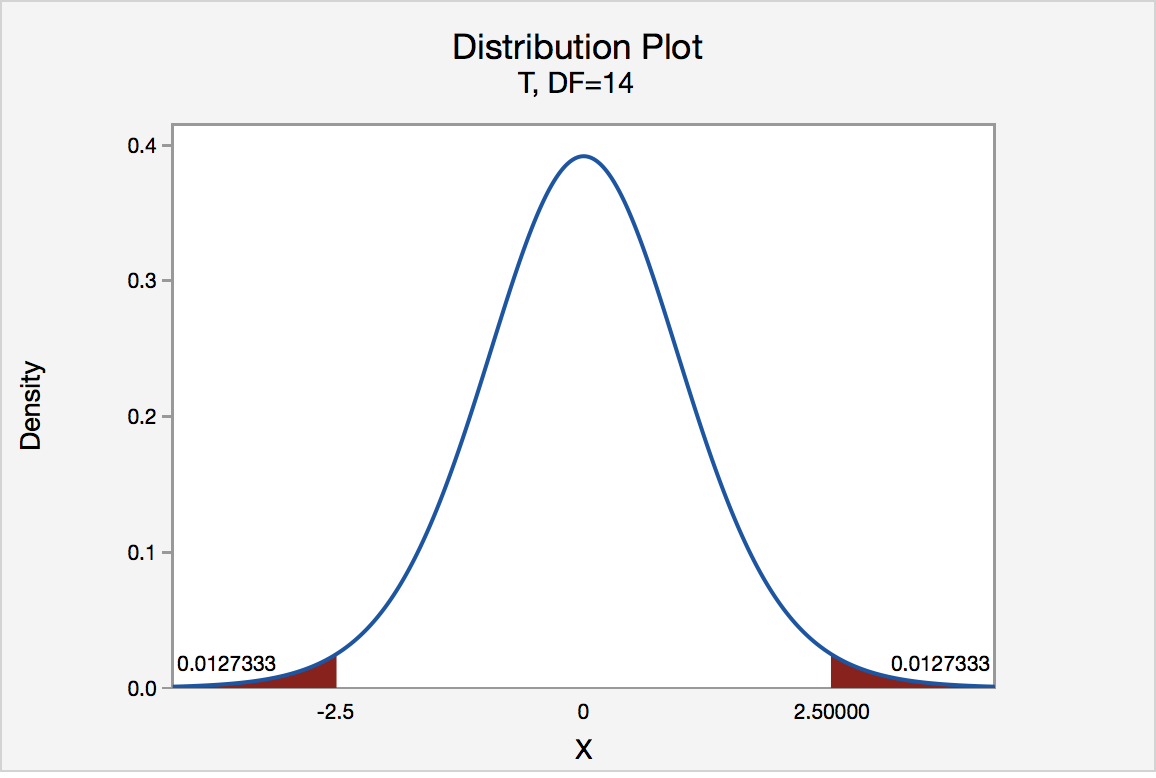
Note that the P -value for a two-tailed test is always two times the P -value for either of the one-tailed tests. The P -value, 0.0254, tells us it is "unlikely" that we would observe such an extreme test statistic t * in the direction of H A if the null hypothesis were true. Therefore, our initial assumption that the null hypothesis is true must be incorrect. That is, since the P -value, 0.0254, is less than α = 0.05, we reject the null hypothesis H 0 : μ = 3 in favor of the alternative hypothesis H A : μ ≠ 3.

Note that we would not reject H 0 : μ = 3 in favor of H A : μ ≠ 3 if we lowered our willingness to make a Type I error to α = 0.01 instead, as the P -value, 0.0254, is then greater than \(\alpha\) = 0.01.

Now that we have reviewed the critical value and P -value approach procedures for each of the three possible hypotheses, let's look at three new examples — one of a right-tailed test, one of a left-tailed test, and one of a two-tailed test.

The good news is that, whenever possible, we will take advantage of the test statistics and P -values reported in statistical software, such as Minitab, to conduct our hypothesis tests in this course.

How to Write Hypothesis Test Conclusions (With Examples)

A   hypothesis test is used to test whether or not some hypothesis about a population parameter is true.

To perform a hypothesis test in the real world, researchers obtain a random sample from the population and perform a hypothesis test on the sample data, using a null and alternative hypothesis:

• Null Hypothesis (H 0 ): The sample data occurs purely from chance.
• Alternative Hypothesis (H A ): The sample data is influenced by some non-random cause.

If the p-value of the hypothesis test is less than some significance level (e.g. α = .05), then we reject the null hypothesis .

Otherwise, if the p-value is not less than some significance level then we fail to reject the null hypothesis .

When writing the conclusion of a hypothesis test, we typically include:

• Whether we reject or fail to reject the null hypothesis.
• The significance level.
• A short explanation in the context of the hypothesis test.

For example, we would write:

We reject the null hypothesis at the 5% significance level.   There is sufficient evidence to support the claim that…

Or, we would write:

We fail to reject the null hypothesis at the 5% significance level.   There is not sufficient evidence to support the claim that…

The following examples show how to write a hypothesis test conclusion in both scenarios.

Example 1: Reject the Null Hypothesis Conclusion

Suppose a biologist believes that a certain fertilizer will cause plants to grow more during a one-month period than they normally do, which is currently 20 inches. To test this, she applies the fertilizer to each of the plants in her laboratory for one month.

She then performs a hypothesis test at a 5% significance level using the following hypotheses:

• H 0 : μ = 20 inches (the fertilizer will have no effect on the mean plant growth)
• H A : μ > 20 inches (the fertilizer will cause mean plant growth to increase)

Suppose the p-value of the test turns out to be 0.002.

Here is how she would report the results of the hypothesis test:

We reject the null hypothesis at the 5% significance level.   There is sufficient evidence to support the claim that this particular fertilizer causes plants to grow more during a one-month period than they normally do.

Example 2: Fail to Reject the Null Hypothesis Conclusion

Suppose the manager of a manufacturing plant wants to test whether or not some new method changes the number of defective widgets produced per month, which is currently 250. To test this, he measures the mean number of defective widgets produced before and after using the new method for one month.

He performs a hypothesis test at a 10% significance level using the following hypotheses:

• H 0 : μ after = μ before (the mean number of defective widgets is the same before and after using the new method)
• H A : μ after ≠ μ before (the mean number of defective widgets produced is different before and after using the new method)

Suppose the p-value of the test turns out to be 0.27.

Here is how he would report the results of the hypothesis test:

We fail to reject the null hypothesis at the 10% significance level.   There is not sufficient evidence to support the claim that the new method leads to a change in the number of defective widgets produced per month.

Additional Resources

The following tutorials provide additional information about hypothesis testing:

Introduction to Hypothesis Testing 4 Examples of Hypothesis Testing in Real Life How to Write a Null Hypothesis

10 Examples of Using Probability in Real Life

Mongodb: how to find document by id, you may also like, how to normalize data between -1 and 1, vba: how to check if string contains another string, how to interpret f-values in a two-way anova, how to create a vector of ones in r (with examples), how to find the mode of a histogram (with example), how to find quartiles in even and odd length datasets.