hypothesis testing logic

Statistical Hypothesis Testing with Microsoft ® Office Excel ® pp 1–10 Cite as

Logic of Hypothesis Testing

• Robert Hirsch 3  
• First Online: 15 July 2022

116 Accesses

Part of the book series: Synthesis Lectures on Mathematics & Statistics ((SLMS))

This chapter begins by describing the hypothesis statistics is designed to test. That hypothesis, known as the null hypothesis, states that things do not differ or there is no association between measurements. If that hypothesis is rejected, we conclude that there are differences or associations. Decisions to reject the null hypothesis are based on P -values. The chapter describes the origin and interpretation of P -values. It also discusses errors that can occur in interpretation of the P -value and how to control them. This discussion addresses the classical or frequentist approach to hypothesis testing. The Bayesian approach takes things further, allowing determination of the probability that the null hypothesis is false given frequentist methods have resulted in rejection of the null hypothesis. Both approaches are applied to the situation in which a study includes several hypothesis tests.

This is a preview of subscription content, log in via an institution .

Buying options

• Available as PDF
• Read on any device
• Instant download
• Own it forever
• Available as EPUB and PDF
• Compact, lightweight edition
• Dispatched in 3 to 5 business days
• Free shipping worldwide - see info
• Durable hardcover edition

Tax calculation will be finalised at checkout

Purchases are for personal use only

Another possible explanation for an observed difference is that there is a bias in the design of the study. For instance, one group might be sicker than the other group. If both chance and bias can be eliminated as likely explanations, the observed difference must be reflecting a causal relationship.

Note that we do not accept the null hypothesis as true if the P -value is greater than 0.05. There is no rule of thumb for how large the P -value needs to be to believe the null hypothesis is true in the frequentist approach.

Note that to use a one-tailed alternative hypothesis, deviations from the null hypothesis must be possible in only one direction. It is not enough to say we do not think that deviations in both directions will occur or to say we are only interested in deviations in one direction.

I have drawn the sampling distribution as a bell-shaped curve. Sampling distributions tend to be bell-shaped regardless of the shape of the distribution of data, if the sample is large enough. This important principle is called the central limit theorem .

We call this the posterior probability because it is the probability of the null hypothesis being true after we know the results of the statistical analysis.

This is often a difficult probability to which to assign a value. There is no analysis that helps. Rather, the research must assign a value based on a subjective guess.

We will learn more about statistical power in Chap. 5 .

Author information

Authors and affiliations.

Overland Park, KS, USA

Robert Hirsch

You can also search for this author in PubMed   Google Scholar

Corresponding author

Correspondence to Robert Hirsch .

Rights and permissions

Reprints and permissions

Copyright information

© 2022 The Author(s), under exclusive license to Springer Nature Switzerland AG

About this chapter

Cite this chapter.

Hirsch, R. (2022). Logic of Hypothesis Testing. In: Statistical Hypothesis Testing with Microsoft ® Office Excel ®. Synthesis Lectures on Mathematics & Statistics. Springer, Cham. https://doi.org/10.1007/978-3-031-04202-7_1

Download citation

DOI : https://doi.org/10.1007/978-3-031-04202-7_1

Published : 15 July 2022

Publisher Name : Springer, Cham

Print ISBN : 978-3-031-04201-0

Online ISBN : 978-3-031-04202-7

eBook Packages : Synthesis Collection of Technology (R0) eBColl Synthesis Collection 11

Share this chapter

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

• Publish with us

Policies and ethics

• Find a journal
• Track your research

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons
• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

8.1: The Elements of Hypothesis Testing

• Last updated
• Save as PDF
• Page ID 130263

Learning Objectives

• To understand the logical framework of tests of hypotheses.
• To learn basic terminology connected with hypothesis testing.
• To learn fundamental facts about hypothesis testing.

Types of Hypotheses

A hypothesis about the value of a population parameter is an assertion about its value. As in the introductory example we will be concerned with testing the truth of two competing hypotheses, only one of which can be true.

Definition: null hypothesis and alternative hypothesis

• The null hypothesis , denoted \(H_0\), is the statement about the population parameter that is assumed to be true unless there is convincing evidence to the contrary.
• The alternative hypothesis , denoted \(H_a\), is a statement about the population parameter that is contradictory to the null hypothesis, and is accepted as true only if there is convincing evidence in favor of it.

Definition: statistical procedure

Hypothesis testing is a statistical procedure in which a choice is made between a null hypothesis and an alternative hypothesis based on information in a sample.

The end result of a hypotheses testing procedure is a choice of one of the following two possible conclusions:

• Reject \(H_0\) (and therefore accept \(H_a\)), or
• Fail to reject \(H_0\) (and therefore fail to accept \(H_a\)).

The null hypothesis typically represents the status quo, or what has historically been true. In the example of the respirators, we would believe the claim of the manufacturer unless there is reason not to do so, so the null hypotheses is \(H_0:\mu =75\). The alternative hypothesis in the example is the contradictory statement \(H_a:\mu <75\). The null hypothesis will always be an assertion containing an equals sign, but depending on the situation the alternative hypothesis can have any one of three forms: with the symbol \(<\), as in the example just discussed, with the symbol \(>\), or with the symbol \(\neq\). The following two examples illustrate the latter two cases.

Example \(\PageIndex{1}\)

A publisher of college textbooks claims that the average price of all hardbound college textbooks is \(\$127.50\). A student group believes that the actual mean is higher and wishes to test their belief. State the relevant null and alternative hypotheses.

The default option is to accept the publisher’s claim unless there is compelling evidence to the contrary. Thus the null hypothesis is \(H_0:\mu =127.50\). Since the student group thinks that the average textbook price is greater than the publisher’s figure, the alternative hypothesis in this situation is \(H_a:\mu >127.50\).

Example \(\PageIndex{2}\)

The recipe for a bakery item is designed to result in a product that contains \(8\) grams of fat per serving. The quality control department samples the product periodically to insure that the production process is working as designed. State the relevant null and alternative hypotheses.

The default option is to assume that the product contains the amount of fat it was formulated to contain unless there is compelling evidence to the contrary. Thus the null hypothesis is \(H_0:\mu =8.0\). Since to contain either more fat than desired or to contain less fat than desired are both an indication of a faulty production process, the alternative hypothesis in this situation is that the mean is different from \(8.0\), so \(H_a:\mu \neq 8.0\).

In Example \(\PageIndex{1}\), the textbook example, it might seem more natural that the publisher’s claim be that the average price is at most \(\$127.50\), not exactly \(\$127.50\). If the claim were made this way, then the null hypothesis would be \(H_0:\mu \leq 127.50\), and the value \(\$127.50\) given in the example would be the one that is least favorable to the publisher’s claim, the null hypothesis. It is always true that if the null hypothesis is retained for its least favorable value, then it is retained for every other value.

Thus in order to make the null and alternative hypotheses easy for the student to distinguish, in every example and problem in this text we will always present one of the two competing claims about the value of a parameter with an equality. The claim expressed with an equality is the null hypothesis. This is the same as always stating the null hypothesis in the least favorable light. So in the introductory example about the respirators, we stated the manufacturer’s claim as “the average is \(75\) minutes” instead of the perhaps more natural “the average is at least \(75\) minutes,” essentially reducing the presentation of the null hypothesis to its worst case.

The first step in hypothesis testing is to identify the null and alternative hypotheses.

The Logic of Hypothesis Testing

Although we will study hypothesis testing in situations other than for a single population mean (for example, for a population proportion instead of a mean or in comparing the means of two different populations), in this section the discussion will always be given in terms of a single population mean \(\mu\).

The null hypothesis always has the form \(H_0:\mu =\mu _0\) for a specific number \(\mu _0\) (in the respirator example \(\mu _0=75\), in the textbook example \(\mu _0=127.50\), and in the baked goods example \(\mu _0=8.0\)). Since the null hypothesis is accepted unless there is strong evidence to the contrary, the test procedure is based on the initial assumption that \(H_0\) is true. This point is so important that we will repeat it in a display:

The test procedure is based on the initial assumption that \(H_0\) is true.

The criterion for judging between \(H_0\) and \(H_a\) based on the sample data is: if the value of \(\overline{X}\) would be highly unlikely to occur if \(H_0\) were true, but favors the truth of \(H_a\), then we reject \(H_0\) in favor of \(H_a\). Otherwise we do not reject \(H_0\).

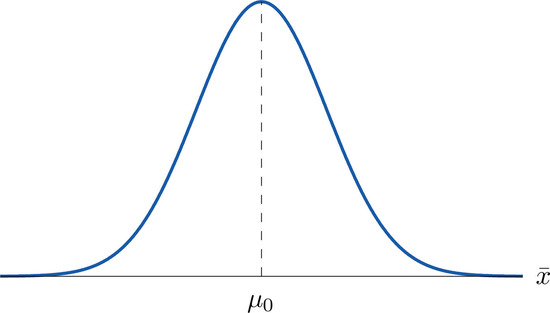
Supposing for now that \(\overline{X}\) follows a normal distribution, when the null hypothesis is true the density function for the sample mean \(\overline{X}\) must be as in Figure \(\PageIndex{1}\): a bell curve centered at \(\mu _0\). Thus if \(H_0\) is true then \(\overline{X}\) is likely to take a value near \(\mu _0\) and is unlikely to take values far away. Our decision procedure therefore reduces simply to:

• if \(H_a\) has the form \(H_a:\mu <\mu _0\) then reject \(H_0\) if \(\bar{x}\) is far to the left of \(\mu _0\);
• if \(H_a\) has the form \(H_a:\mu >\mu _0\) then reject \(H_0\) if \(\bar{x}\) is far to the right of \(\mu _0\);
• if \(H_a\) has the form \(H_a:\mu \neq \mu _0\) then reject \(H_0\) if \(\bar{x}\) is far away from \(\mu _0\) in either direction.

Think of the respirator example, for which the null hypothesis is \(H_0:\mu =75\), the claim that the average time air is delivered for all respirators is \(75\) minutes. If the sample mean is \(75\) or greater then we certainly would not reject \(H_0\) (since there is no issue with an emergency respirator delivering air even longer than claimed).

If the sample mean is slightly less than \(75\) then we would logically attribute the difference to sampling error and also not reject \(H_0\) either.

Values of the sample mean that are smaller and smaller are less and less likely to come from a population for which the population mean is \(75\). Thus if the sample mean is far less than \(75\), say around \(60\) minutes or less, then we would certainly reject \(H_0\), because we know that it is highly unlikely that the average of a sample would be so low if the population mean were \(75\). This is the rare event criterion for rejection: what we actually observed \((\overline{X}<60)\) would be so rare an event if \(\mu =75\) were true that we regard it as much more likely that the alternative hypothesis \(\mu <75\) holds.

In summary, to decide between \(H_0\) and \(H_a\) in this example we would select a “rejection region” of values sufficiently far to the left of \(75\), based on the rare event criterion, and reject \(H_0\) if the sample mean \(\overline{X}\) lies in the rejection region, but not reject \(H_0\) if it does not.

The Rejection Region

Each different form of the alternative hypothesis Ha has its own kind of rejection region:

• if (as in the respirator example) \(H_a\) has the form \(H_a:\mu <\mu _0\), we reject \(H_0\) if \(\bar{x}\) is far to the left of \(\mu _0\), that is, to the left of some number \(C\), so the rejection region has the form of an interval \((-\infty ,C]\);
• if (as in the textbook example) \(H_a\) has the form \(H_a:\mu >\mu _0\), we reject \(H_0\) if \(\bar{x}\) is far to the right of \(\mu _0\), that is, to the right of some number \(C\), so the rejection region has the form of an interval \([C,\infty )\);
• if (as in the baked good example) \(H_a\) has the form \(H_a:\mu \neq \mu _0\), we reject \(H_0\) if \(\bar{x}\) is far away from \(\mu _0\) in either direction, that is, either to the left of some number \(C\) or to the right of some other number \(C′\), so the rejection region has the form of the union of two intervals \((-\infty ,C]\cup [C',\infty )\).

The key issue in our line of reasoning is the question of how to determine the number \(C\) or numbers \(C\) and \(C′\), called the critical value or critical values of the statistic, that determine the rejection region.

Definition: critical values

The critical value or critical values of a test of hypotheses are the number or numbers that determine the rejection region.

Suppose the rejection region is a single interval, so we need to select a single number \(C\). Here is the procedure for doing so. We select a small probability, denoted \(\alpha\), say \(1\%\), which we take as our definition of “rare event:” an event is “rare” if its probability of occurrence is less than \(\alpha\). (In all the examples and problems in this text the value of \(\alpha\) will be given already.) The probability that \(\overline{X}\) takes a value in an interval is the area under its density curve and above that interval, so as shown in Figure \(\PageIndex{2}\) (drawn under the assumption that \(H_0\) is true, so that the curve centers at \(\mu _0\)) the critical value \(C\) is the value of \(\overline{X}\) that cuts off a tail area \(\alpha\) in the probability density curve of \(\overline{X}\). When the rejection region is in two pieces, that is, composed of two intervals, the total area above both of them must be \(\alpha\), so the area above each one is \(\alpha /2\), as also shown in Figure \(\PageIndex{2}\).

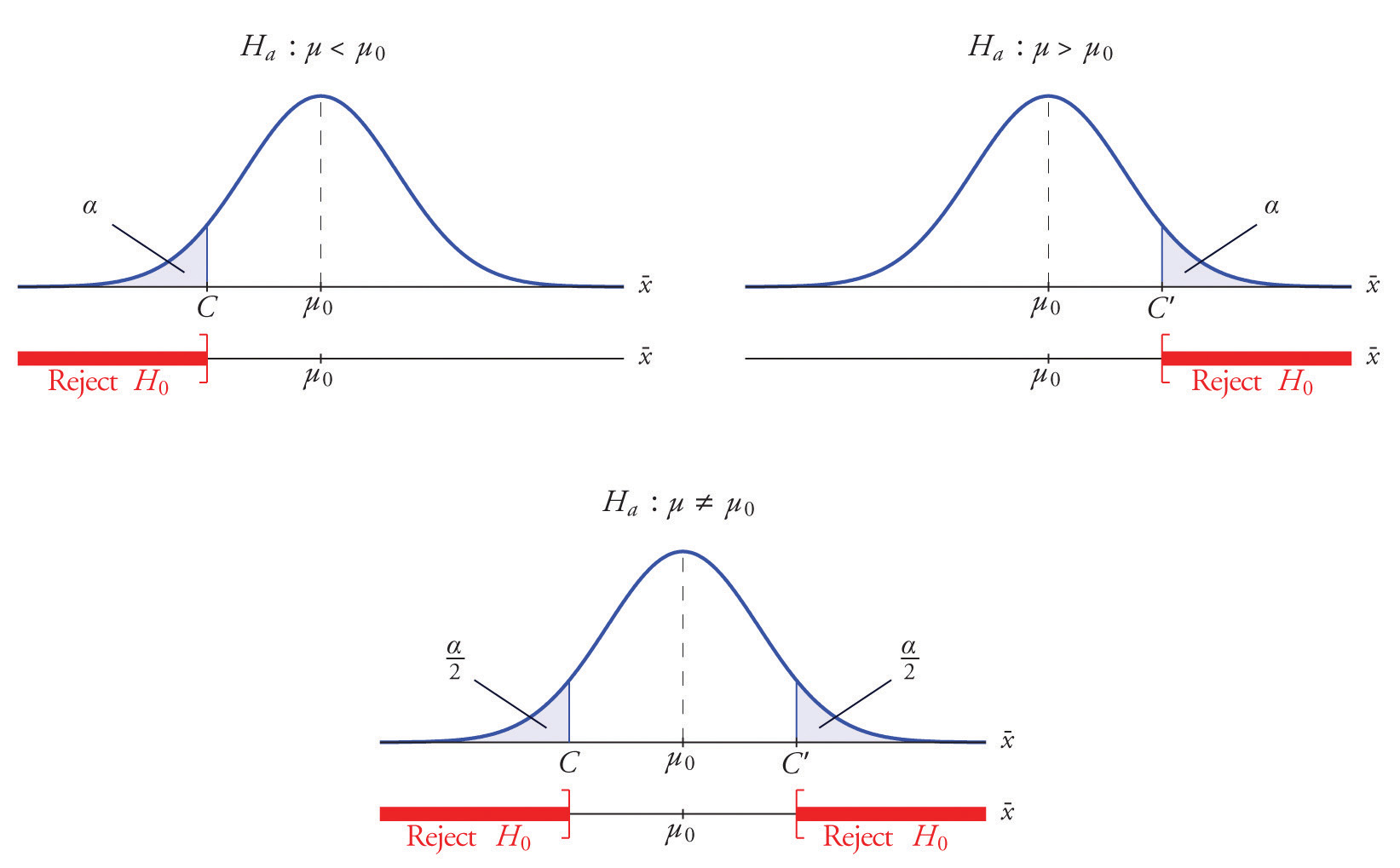
The number \(\alpha\) is the total area of a tail or a pair of tails.

Example \(\PageIndex{3}\)

In the context of Example \(\PageIndex{2}\), suppose that it is known that the population is normally distributed with standard deviation \(\alpha =0.15\) gram, and suppose that the test of hypotheses \(H_0:\mu =8.0\) versus \(H_a:\mu \neq 8.0\) will be performed with a sample of size \(5\). Construct the rejection region for the test for the choice \(\alpha =0.10\). Explain the decision procedure and interpret it.

If \(H_0\) is true then the sample mean \(\overline{X}\) is normally distributed with mean and standard deviation

\[\begin{align} \mu _{\overline{X}} &=\mu \nonumber \\[5pt] &=8.0 \nonumber \end{align} \nonumber \]

\[\begin{align} \sigma _{\overline{X}}&=\dfrac{\sigma}{\sqrt{n}} \nonumber \\[5pt] &= \dfrac{0.15}{\sqrt{5}} \nonumber\\[5pt] &=0.067 \nonumber \end{align} \nonumber \]

Since \(H_a\) contains the \(\neq\) symbol the rejection region will be in two pieces, each one corresponding to a tail of area \(\alpha /2=0.10/2=0.05\). From Figure 7.1.6, \(z_{0.05}=1.645\), so \(C\) and \(C′\) are \(1.645\) standard deviations of \(\overline{X}\) to the right and left of its mean \(8.0\):

\[C=8.0-(1.645)(0.067) = 7.89 \; \; \text{and}\; \; C'=8.0 + (1.645)(0.067) = 8.11 \nonumber \]

The result is shown in Figure \(\PageIndex{3}\). α = 0.1

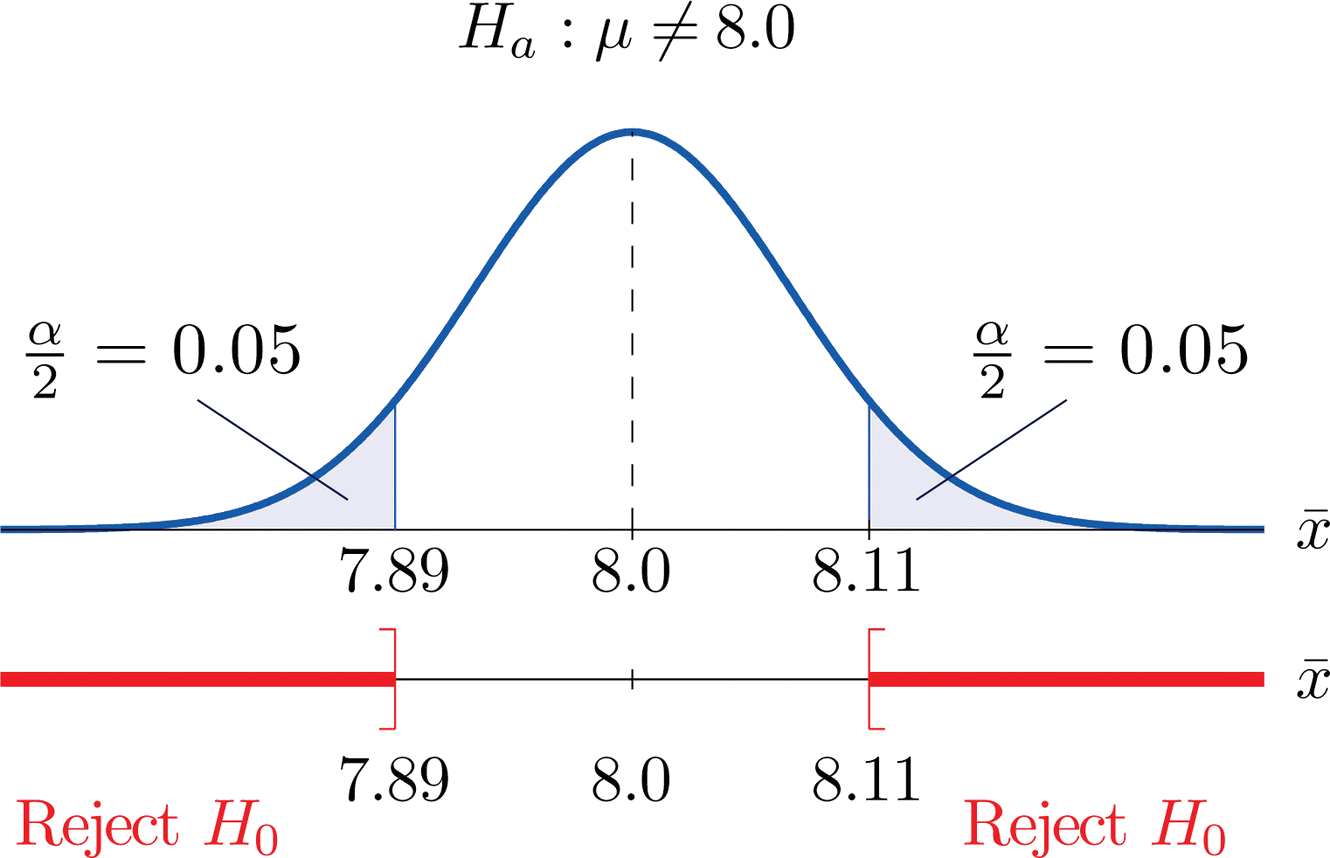
The decision procedure is: take a sample of size \(5\) and compute the sample mean \(\bar{x}\). If \(\bar{x}\) is either \(7.89\) grams or less or \(8.11\) grams or more then reject the hypothesis that the average amount of fat in all servings of the product is \(8.0\) grams in favor of the alternative that it is different from \(8.0\) grams. Otherwise do not reject the hypothesis that the average amount is \(8.0\) grams.

The reasoning is that if the true average amount of fat per serving were \(8.0\) grams then there would be less than a \(10\%\) chance that a sample of size \(5\) would produce a mean of either \(7.89\) grams or less or \(8.11\) grams or more. Hence if that happened it would be more likely that the value \(8.0\) is incorrect (always assuming that the population standard deviation is \(0.15\) gram).

Because the rejection regions are computed based on areas in tails of distributions, as shown in Figure \(\PageIndex{2}\), hypothesis tests are classified according to the form of the alternative hypothesis in the following way.

Definitions: Test classifications

• If \(H_a\) has the form \(\mu \neq \mu _0\) the test is called a two-tailed test .
• If \(H_a\) has the form \(\mu < \mu _0\) the test is called a left-tailed test .
• If \(H_a\) has the form \(\mu > \mu _0\)the test is called a right-tailed test .

Each of the last two forms is also called a one-tailed test .

Two Types of Errors

The format of the testing procedure in general terms is to take a sample and use the information it contains to come to a decision about the two hypotheses. As stated before our decision will always be either

• reject the null hypothesis \(H_0\) in favor of the alternative \(H_a\) presented, or
• do not reject the null hypothesis \(H_0\) in favor of the alternative \(H_0\) presented.

There are four possible outcomes of hypothesis testing procedure, as shown in the following table:

As the table shows, there are two ways to be right and two ways to be wrong. Typically to reject \(H_0\) when it is actually true is a more serious error than to fail to reject it when it is false, so the former error is labeled “ Type I ” and the latter error “ Type II ”.

Definition: Type I and Type II errors

In a test of hypotheses:

• A Type I error is the decision to reject \(H_0\) when it is in fact true.
• A Type II error is the decision not to reject \(H_0\) when it is in fact not true.

Unless we perform a census we do not have certain knowledge, so we do not know whether our decision matches the true state of nature or if we have made an error. We reject \(H_0\) if what we observe would be a “rare” event if \(H_0\) were true. But rare events are not impossible: they occur with probability \(\alpha\). Thus when \(H_0\) is true, a rare event will be observed in the proportion \(\alpha\) of repeated similar tests, and \(H_0\) will be erroneously rejected in those tests. Thus \(\alpha\) is the probability that in following the testing procedure to decide between \(H_0\) and \(H_a\) we will make a Type I error.

Definition: level of significance

The number \(\alpha\) that is used to determine the rejection region is called the level of significance of the test. It is the probability that the test procedure will result in a Type I error .

The probability of making a Type II error is too complicated to discuss in a beginning text, so we will say no more about it than this: for a fixed sample size, choosing \(alpha\) smaller in order to reduce the chance of making a Type I error has the effect of increasing the chance of making a Type II error . The only way to simultaneously reduce the chances of making either kind of error is to increase the sample size.

Standardizing the Test Statistic

Hypotheses testing will be considered in a number of contexts, and great unification as well as simplification results when the relevant sample statistic is standardized by subtracting its mean from it and then dividing by its standard deviation. The resulting statistic is called a standardized test statistic . In every situation treated in this and the following two chapters the standardized test statistic will have either the standard normal distribution or Student’s \(t\)-distribution.

Definition: hypothesis test

A standardized test statistic for a hypothesis test is the statistic that is formed by subtracting from the statistic of interest its mean and dividing by its standard deviation.

For example, reviewing Example \(\PageIndex{3}\), if instead of working with the sample mean \(\overline{X}\) we instead work with the test statistic

\[\frac{\overline{X}-8.0}{0.067} \nonumber \]

then the distribution involved is standard normal and the critical values are just \(\pm z_{0.05}\). The extra work that was done to find that \(C=7.89\) and \(C′=8.11\) is eliminated. In every hypothesis test in this book the standardized test statistic will be governed by either the standard normal distribution or Student’s \(t\)-distribution. Information about rejection regions is summarized in the following tables:

Every instance of hypothesis testing discussed in this and the following two chapters will have a rejection region like one of the six forms tabulated in the tables above.

No matter what the context a test of hypotheses can always be performed by applying the following systematic procedure, which will be illustrated in the examples in the succeeding sections.

Systematic Hypothesis Testing Procedure: Critical Value Approach

• Identify the null and alternative hypotheses.
• Identify the relevant test statistic and its distribution.
• Compute from the data the value of the test statistic.
• Construct the rejection region.
• Compare the value computed in Step 3 to the rejection region constructed in Step 4 and make a decision. Formulate the decision in the context of the problem, if applicable.

The procedure that we have outlined in this section is called the “Critical Value Approach” to hypothesis testing to distinguish it from an alternative but equivalent approach that will be introduced at the end of Section 8.3.

Key Takeaway

• A test of hypotheses is a statistical process for deciding between two competing assertions about a population parameter.
• The testing procedure is formalized in a five-step procedure.

6a.2 - Steps for Hypothesis Tests

The logic of hypothesis testing.

A hypothesis, in statistics, is a statement about a population parameter, where this statement typically is represented by some specific numerical value. In testing a hypothesis, we use a method where we gather data in an effort to gather evidence about the hypothesis.

How do we decide whether to reject the null hypothesis?

• If the sample data are consistent with the null hypothesis, then we do not reject it.
• If the sample data are inconsistent with the null hypothesis, but consistent with the alternative, then we reject the null hypothesis and conclude that the alternative hypothesis is true.

Six Steps for Hypothesis Tests

In hypothesis testing, there are certain steps one must follow. Below these are summarized into six such steps to conducting a test of a hypothesis.

• Set up the hypotheses and check conditions : Each hypothesis test includes two hypotheses about the population. One is the null hypothesis, notated as \(H_0 \), which is a statement of a particular parameter value. This hypothesis is assumed to be true until there is evidence to suggest otherwise. The second hypothesis is called the alternative, or research hypothesis, notated as \(H_a \). The alternative hypothesis is a statement of a range of alternative values in which the parameter may fall. One must also check that any conditions (assumptions) needed to run the test have been satisfied e.g. normality of data, independence, and number of success and failure outcomes.
• Decide on the significance level, \(\alpha \): This value is used as a probability cutoff for making decisions about the null hypothesis. This alpha value represents the probability we are willing to place on our test for making an incorrect decision in regards to rejecting the null hypothesis. The most common \(\alpha \) value is 0.05 or 5%. Other popular choices are 0.01 (1%) and 0.1 (10%).
• Calculate the test statistic: Gather sample data and calculate a test statistic where the sample statistic is compared to the parameter value. The test statistic is calculated under the assumption the null hypothesis is true and incorporates a measure of standard error and assumptions (conditions) related to the sampling distribution.
• Calculate probability value (p-value), or find the rejection region: A p-value is found by using the test statistic to calculate the probability of the sample data producing such a test statistic or one more extreme. The rejection region is found by using alpha to find a critical value; the rejection region is the area that is more extreme than the critical value. We discuss the p-value and rejection region in more detail in the next section.
• Make a decision about the null hypothesis: In this step, we decide to either reject the null hypothesis or decide to fail to reject the null hypothesis. Notice we do not make a decision where we will accept the null hypothesis.
• State an overall conclusion : Once we have found the p-value or rejection region, and made a statistical decision about the null hypothesis (i.e. we will reject the null or fail to reject the null), we then want to summarize our results into an overall conclusion for our test.

We will follow these six steps for the remainder of this Lesson. In the future Lessons, the steps will be followed but may not be explained explicitly.

Step 1 is a very important step to set up correctly. If your hypotheses are incorrect, your conclusion will be incorrect. In this next section, we practice with Step 1 for the one sample situations.

Statistical Modeling: A Fresh Approach

Chapter 13 the logic of hypothesis testing.

Extraordinary claims demand extraordinary evidence. - Carl Sagan (1934-1996), astronomer

The test of a first-rate intelligence is the ability to hold two opposing ideas in mind at the same time and still retain the ability to function. - F. Scott Fitzgerald (1896-1940), novelist

A hypothesis test is a standard format for assessing statistical evidence. It is ubiquitous in scientific literature, most often appearing in the form of statements of statistical significance and notations like “p < 0.01” that pepper scientific journals.

Hypothesis testing involves a substantial technical vocabulary: null hypotheses, alternative hypotheses, test statistics, significance, power, p-values, and so on. The last section of this chapter lists the terms and gives definitions.

The technical aspects of hypothesis testing arise because it is a highly formal and quite artificial way of reasoning. This isn’t a criticism. Hypothesis testing is this way because the “natural” forms of reasoning are inappropriate. To illustrate why, consider an example.

13.1 Example: Ups and downs in the stock market

The stock market’s ups and downs are reported each working day. Some people make money by investing in the market, some people lose. Is there reason to believe that there is a trend in the market that goes beyond the random-seeming daily ups and downs?

Figure 13.1 shows the closing price of the Dow Jones Industrial Average stock index for a period of about 10 years up until just before the 2008 recession, a period when stocks were considered a good investment. It’s evident that the price is going up and down in an irregular way, like a random walk. But it’s also true that the price at the end of the period is much higher than the price at the start of the period.

Figure 13.1: The closing price of the DJIA each day over 2500 trading days - a roughly 10 year period from the close on Dec. 5, 1997 to the close on Nov. 14, 2007. See Section 1.9 for an update on stock prices.

Is there a trend or is this just a random walk? It’s undeniable that there are fluctuations that look something like a random walk, but is there a trend buried under the fluctuations?

As phrased, the question contrasts two different possible hypotheses. The first is that the market is a pure random walk. The second is that the market has a systematic trend in addition to the random walk.

The natural question to ask is this: Which hypothesis is right?

Each of the hypotheses is actually a model: a representation of the world for a particular purpose. But each of the models is an incomplete representation of the world, so each is wrong.

It’s tempting to rephrase the question slightly to avoid the simplistic idea of right versus wrong models: Which hypothesis is a better approximation to the real world? That’s a nice question, but how to answer it in practice? To say how each hypothesis differs from the real world, you need to know already what the real world is like: Is there a trend in stock prices or not? That approach won’t take you anywhere.

Another idea: Which hypothesis gives a better match to the data? This seems a simple matter: fit each of the models to the data and see which one gives the better fit. But recall that even junk model terms can lead to smaller residuals. In the case of the stock market data, it happens that the model that includes a trend will almost always give smaller residuals than the pure random walk model, even if the data really do come from a pure random walk.

The logic of hypothesis testing avoids these problems. The basic idea is to avoid having to reason about the real world by setting up a hypothetical world that is completely understood. The observed patterns of the data are then compared to what would be generated in the hypothetical world. If they don’t match, then there is reason to doubt that the data support the hypothesis.

13.2 An Example of a Hypothesis Test

To illustrate the basic structure of a hypothesis test, here is one using the stock-market data.

The test statistic is a number that is calculated from the data and summarizes the observed patterns of the data. A test statistic might be a model coefficient or an R² value or something else. For the stock market data, it’s sensible to use as the test statistic the start-to-end dollar difference in prices over the 2500-day period. The observed value of this test statistic is $5446 - the DJIA stocks went up by this amount over the 10-year period.

The start-to-end difference can be used to test the hypothesis that the stock market is a random walk. (The reason to choose the random walk hypothesis for testing instead of the trend hypothesis will be discussed later.)

In order to carry out the hypothesis test, you construct a conjectural or hypothetical world in which the hypothesis is true. You can do this by building a simulation of that world and generating data from the simulation. Traditionally, such simulations have been implemented using probability theory and algebra to carry out the calculations of what results are likely in the hypothetical world. It’s also possible to use direct computer simulation of the hypothetical world.

The challenge is to create a hypothetical world that is relevant to the real world. It would not, for example, be relevant to hypothesize that stock prices never change, nor would it be relevant to imaging that they change by an unrealistic amount. Later chapters will introduce a few techniques for doing this in statistical models. For this stock-price hypothesis, we’ll imagine a hypothetical world in which prices change randomly up and down by the same daily amounts that they were seen to change in the real world.

Figure 13.2 shows a few examples of stock prices in the hypothetical world where prices are equally likely to go up or down each day by the same daily percentages seen in the actual data.

Figure 13.2: Two simulations of stock prices in a hypothetical world where the day-to-day change is equally likely to be up or down.

By generating many such simulations, and measuring from each individual simulation the start-to-end change in price, you get an indication of the range of likely outcomes in the hypothetical world. This is shown in Figure 13.3 , which also shows the value observed in the real world - a price increase of $5446.

Figure 13.3: The distribution of start-to-end differences in stock price in the hypothetical world where that day-to-day changes in price are equally likely to be up or down by the proportions observed in the real world. The value observed in the data, $5446, is marked with a vertical line.

Since the observed start-to-end change in price is well within the possibilities generated by the simulation, it’s tempting to say, “the observations support the hypothesis.” For reasons discussed in the next section, however, the logically permitted conclusion is stiff and unnatural: We fail to reject the hypothesis.

13.3 Inductive and Deductive Reasoning

Hypothesis testing involves a combination of two different styles of reasoning: deduction and induction. In the deductive part, the hypothesis tester makes an assumption about how the world works and draws out, deductively, the consequences of this assumption: what the observed value of the test statistic should be if the hypothesis is true. For instance, the hypothesis that stock prices are a random walk was translated into a statement of the probability distribution of the start-to-end price difference.

In the inductive part of a hypothesis test, the tester compares the actual observations to the deduced consequences of the assumptions and decides whether the observations are consistent with them.

Deductive Reasoning

Deductive reasoning involves a series of rules that bring you from given assumptions to the consequences of those assumptions. For example, here is a form of deductive reasoning called a syllogism :

• Assumption 1 : No healthy food is fattening.
• Assumption 2 : All cakes are fattening.
• Conclusion : No cakes are healthy.

The actual assumptions involved here are questionable, but the pattern of logic is correct. If the assumptions were right, the conclusion would be right also.

Deductive reasoning is the dominant form in mathematics. It is at the core of mathematical proofs and lies behind the sorts of manipulations used in algebra. For example, the equation 3x + 2 = 8 is a kind of assumption. Another assumption, known to be true for numbers, is that subtracting the same amount from both sides of an equation preserves the equality. So you can subtract 2 from both sides to get 3x = 6. The deductive process continues - divide both sides by 3 - to get a new statement, x = 2, that is a logical consequence of the initial assumption. Of course, if the assumption 3x + 2 = 8 was wrong, then the conclusion x = 2 would be wrong too.

The contrapositive is a way of recasting an assumption in a new form that will be true so long as the original assumption is true. For example, suppose the original assumption is, “My car is red.” Another way to state this assumption is as a statement of implication, an if-then statement:

• Assumption : If it is my car, then it is red.

To form the contrapositive, you re-arrange the assumption to produce another statement:

• Contrapositive If it is not red, then it is not my car.

Any assumption of the form “if [statement 1] then [statement 2]” has a contrapositive. In the example, statement 1 is “it is my car.” Statement 2 is “it is red.” The contrapositive looks like this:

• Contrapositive : If [negate statement 2] then [negate statement 1].

The contrapositive is, like algebraic manipulation, a re-rearrangement: reverse and negate. Reversing means switching the order of the two statements in the if-then structure. Negating a statement means saying the opposite. The negation of “it is red” is “it is not red.” The negation of “it is my car” is “it is not my car.” (It would be wrong to say that the negation of “it is my car” is “it is your car.” Clearly it’s true that if it is your car, then it is not my car. But there are many ways that the car can be not mine and yet not be yours. There are, after all, many other people in the world than you and me!)

Contrapositives often make intuitive sense to people. That is, people can see that a contrapostive statement is correct even if they don’t know the name of the logical re-arrangement. For instance, here is a variety of ways of re-arranging the two clauses in the assumption, “If that is my car, then it is red.” Some of the arrangements are logically correct, and some aren’t.

Original Assumption : If it is my car, then it is red.

Negate first statement: If it is not my car, then it is red.

Negate only second statement: If it is my car, then it is not red.

Negate both statements: If it is not my car, then it is not red.

Reverse statements: If it is red, then it is my car.

Reverse and negate first: If it is red, then it is not my car.

Reverse and negate second: If it is not red, then it is my car.

Reverse and negate both - the contrapositive: If it is not red, then it is not my car.

Inductive Reasoning

In contrast to deductive reasoning, inductive reasoning involves generalizing or extrapolating from a set of observations to conclusions. An observation is not an assumption: it is something we see or otherwise perceive. For instance, you can go to Australia and see that kangaroos hop on two legs. Every kangaroo you see is hopping on two legs. You conclude, inductively, that all kangaroos hop on two legs.

Inductive conclusions are not necessarily correct. There might be one-legged kangaroos. That you haven’t seen them doesn’t mean they can’t exist. Indeed, Europeans believed that all swans are white until explorers discovered that there are black swans in Australia.

Suppose you conduct an experiment involving 100 people with fever. You give each of them aspirin and observe that in all 100 the fever is reduced. Are you entitled to conclude that giving aspirin to a person with fever will reduce the fever? Not really. How do you know that there are no people who do not respond to aspirin and who just happened not be be included in your study group?

Perhaps you’re tempted to hedge by weakening your conclusion: “Giving aspirin to a person with fever will reduce the fever most of the time.” This seems reasonable, but it is still not necessarily true. Perhaps the people in you study had a special form of fever-producing illness and that most people with fever have a different form.

By the standards of deductive reasoning, inductive reasoning does not work. No reasonable person can argue about the deductive, contrapositive reasoning concerning the red car. But reasonable people can very well find fault with the conclusions drawn from the study of aspirin.

Here’s the difficulty. If you stick to valid deductive reasoning, you will draw conclusions that are correct given that your assumptions are correct. But how can you know if your assumptions are correct? How can you make sure that your assumptions adequately reflect the real world? At a practical level, most knowledge of the world comes from observations and induction.

The philosopher David Hume noted the everyday inductive “fact” that food nourishes us, a conclusion drawn from everyday observations that people who eat are nourished and people who do not eat waste away. Being inductive, the conclusion is suspect. Still, it would be a foolish person who refuses to eat for want of a deductive proof of the benefits of food.

Inductive reasoning may not provide a proof, but it is nevertheless useful.

13.4 The Null Hypothesis

A key aspect of hypothesis testing is the choice of the hypothesis to test. The stock market example involved testing the random-walk hypothesis rather than the trend hypothesis. Why? After all, the hypothesis of a trend is more interesting than the random-walk hypothesis; it’s more likely to be useful if true.

It might seem obvious that the hypothesis you should test is the hypothesis that you are most interested in. But this is wrong.

In a hypothesis test one assumes that the hypothesis to be tested is true and draws out the consequences of that assumption in a deductive process. This can be written as an if-then statement:

If hypothesis H is true, then the test statistic S will be drawn from a probability distribution P.

For example, in the stock market test, the assumption that the day-to-day price change is random leads to the conclusion that the test statistic - the start-to-end price difference - will be a draw from the distribution shown in Figure 13.3 .

The inductive part of the test involves comparing the observed value of the test statistic S to the distribution P. There are two possible outcomes of this comparison:

• Agreement : S is a plausible outcome from P.
• Disagreement : S is not a plausible outcome from P.

Suppose the outcome is agreement between S and P. What can be concluded? Not much. Recall the statement “If it is my car, then it is red.” An observation of a red car does not legitimately lead to the conclusion that the car is mine. For an if-then statement to be applicable to observations, one needs to observe the if-part of the statement, not the then-part.

An outcome of disagreement gives a more interesting result, because the contrapositive gives logical traction to the observation; “If it is not red, then it is not my car.” Seeing “not red” implies “not my car.” Similarly, seeing that S is not a plausible outcome from P, tells you that H is not a plausible possibility. In such a situation, you can legitimately say, “I reject the hypothesis.”

Ironically, in the case of observing agreement between S and P, the only permissible statement is, “I fail to reject the hypothesis.” You certainly aren’t entitled to say that the evidence causes you to accept the hypothesis.

This is an emotionally unsatisfying situation. If your observations are consistent with your hypothesis, you certainly want to accept the hypothesis. But that is not an acceptable conclusion when performing a formal hypothesis test. There are only two permissible conclusions from a formal hypothesis test:

• I reject the hypothesis.
• I fail to reject the hypothesis.

In choosing a hypothesis to test, you need to keep in mind two criteria.

• Criterion 1 : The only possible interesting outcome of a hypothesis test is “I reject the hypothesis.” So make sure to pick a hypothesis that it will be interesting to reject.

The role of the hypothesis is to be refuted or nullified, so it is called the null hypothesis .

What sorts of statements are interesting to reject? Often these take the form of the conventional wisdom or a claim of no effect .

For example, in comparing two fever-reducing drugs, an appropriate null hypothesis is that the two drugs have the same effect. If you reject the null, you can say that they don’t have the same effect. But if you fail to reject the null, you’re in much the same position as before you started the study.

Failing to reject the null may mean that the null is true, but it equally well may mean only that your work was not adequate: not enough data, not a clever enough experiment, etc. Rejecting the null can reasonably be taken to indicate that the null hypothesis is false, but failing to reject the null tells you very little.

• Criterion 2 : To perform the deductive stage of the test, you need to be able to calculate the range of likely outcomes of the test statistic. This means that the hypothesis needs to be specific.

The assumption that stock prices are a random walk has very definite consequences for how big a start-to-end change you can expect to see. On the other hand, the assumption “there is a trend” leaves open the question of how big the trend is. It’s not specific enough to be able to figure out the consequences.

13.5 The p-value

One of the consequences of randomness is that there isn’t a completely clean way to say whether the observations fail to match the consequences of the null hypothesis. In principle, this is a problem even with simple statements like “the car is red.” There is a continuous range of colors and at some point one needs to make a decision about how orange the car can be before it stops being red.

Figure 13.3 shows the probability distribution for the start-to-end stock price change under the null hypothesis that stock prices are a random walk. The observed value of the test statistic, $5446, falls under the tall part of the curve - it’s a plausible outcome of a random draw from the probability distribution.

The conventional way to measure the plausibility of an outcome is by a p-value . The p-value of an observation is always calculated with reference to a probability distribution derived from the null hypothesis.

P-values are closely related to percentiles. The observed value $5446 falls at the 81rd percentile of the distribution. An observation that’s at or beyond the extremes of the distribution is implausible. This would correspond to either very high percentiles or very low percentiles. Being at the 81rd percentile implies that 19 percent of draws would be even more extreme, falling even further to the right than $5446.

The p-value is the fraction of possible draws from the distribution that are as extreme or more extreme than the observed value. If the concern is only with values bigger than $5446, then the p-value is 0.19.

A small p-value indicates that the actual value of the test statistic is quite surprising as an outcome from the null hypothesis. A large p-value means that the test statistic value is run of the mill, not surprising, not enough to satisfy the “if” part of the contrapositive.

The convention in hypothesis testing is to consider the observation as being implausible when the p-value is less than 0.05. In the stock market example, the p-value is larger than 0.05, so the outcome is to fail to reject the null hypothesis that stock prices are a random walk with no trend.

13.6 Rejecting by Mistake

The p-value for the hypothesis test of the possible trend in stock-price was 0.19, not small enough to justify rejecting the null hypothesis that stock prices are a random walk with no trend. A smaller p-value, one less than 0.05 by convention, would have led to rejection of the null. The small p-value would have indicated that the observed value of the test statistic was implausible in a world where the null hypothesis is true.

Now turn this around. Suppose the null hypothesis really were true; suppose stock prices really are a random walk with no trend. In such a world, it’s still possible to see an implausible value of the test statistic. But, if the null hypothesis is true, then seeing an implausible value is misleading; rejecting the null is a mistake. This sort of mistake is called a Type I error .

Such mistakes are not uncommon. In a world where the null is true - the only sort of world where you can falsely reject the null - they will happen 5% of the time so long as the threshold for rejecting the null is a p-value of 0.05.

The way to avoid such mistakes is to lower the p-value threshold for rejecting the null. Lowering it to, say, 0.01, would make it harder to mistakenly reject the null. On the other hand, it would also make it harder to correctly reject the null in a world where the null ought to be rejected.

The threshold value of the p-value below which the null should be rejected is a probability: the probability of rejecting the null in a world where the null hypothesis is true. This probability is called the significance level of the test.

It’s important to remember that the significance level is a conditional probability . It is the probability of rejecting the null in a world where the null hypothesis is actually true. Of course that’s a hypothetical world, not necessarily the real world.

13.7 Failing to Reject

In the stock-price example, the large p-value of 0.19 led to a failure to reject the null hypothesis that stock prices are a random walk. Such a failure doesn’t mean that the null hypothesis is true, although it’s encouraging news to people who want to believe that the null hypothesis is true.

You never get to “accept the null” because there are reasons why, even if the null were wrong, it might not have been rejected:

• You might have been unlucky. The randomness of the sample might have obscured your being able to see the trend in stock prices.
• You might not have had enough data. Perhaps the trend is small and can’t easily be seen.
• Your test statistic might not be sensitive to the ways in which the system differs from the null hypothesis. For instance, suppose that there is an small average tendency for each day’s activity on the stock market to undo the previous day’s change: the walk isn’t exactly random. Looking for large values of the start-to-end price difference will not reveal this violation of the null. A more sensitive test statistic would be the correlation between price changes on successive days.

A helpful idea in hypothesis testing is the alternative hypothesis : the pet idea of what the world is like if the null hypothesis is wrong. The alternative hypothesis plays the role of the thing that you would like to prove. In the hypothesis-testing drama, this is a very small role, since the only possible outcomes of a hypothesis test are (1) reject the null and (2) fail to reject the null. The alternative hypothesis is not directly addressed by the outcome of a hypothesis test.

The role of the alternative hypothesis is to guide you in interpreting the results if you do fail to reject the null. The alternative hypothesis is also helpful in deciding how much data to collect.

To illustrate, suppose that the stock market really does have a trend hidden inside the random day-to-day fluctuations with a standard deviation of $106.70. Imagine that the trend is $2 per day: a pet hypothesis.

Suppose the world really were like the alternative hypothesis. What is the probability that, in such a world, you would end up failing to reject the null hypothesis? Such a mistake, where you fail to reject the null in a world where the alternative is actually true, is called a Type II error .

This logic can be confusing at first. It’s tempting to reason that, if the alternative hypothesis is true, then the null must be false. So how could you fail to reject the null? And, if the alternative hypothesis is assumed to be true, why would you even consider the null hypothesis in the first place?

Keep in mind that neither the null hypothesis nor the alternative hypothesis should be taken as “true.” They are just competing hypotheses, conjectures used to answer “what-if?” questions.

Aside: Calculating a Power

Here are the steps in calculating the power of the hypothesis test of stock market prices. The null hypothesis is that prices are a pure random walk as illustrated in Figure 13.2 . The alternative hypothesis is that in addition to the random component, the stock prices have a systematic trend of increasing by $2 per day.

• Go back to the null hypothesis world and find the thresholds for the test statistic that would cause you to reject the null hypothesis. Referring to Figure , you can see that a test statistic of $11,000 would have produced a p-value of 0.05.
• Now return to the alternative hypothesis world. In this world, what is the probability that the test statistic would have been bigger than $11,000? This question can be answered by the same sort of simulation as in Figure but with a $2 price increase added each day. Doing the calculation gives a probability of \(0.16\) .

Section 13.7 discusses power calculations for models.

The probability of rejecting the null in a world where the alternative is true is called the power of the hypothesis test. Of course, if the alternative is true, then it’s completely appropriate to reject the null, so a large power is desirable.

A power calculation involves considering both the null and alternative hypotheses. The aside in Section 13.7 shows the logic applied to the stock-market question. It results in a power of 16%.

The power of 16% for the stock market test means that even if the pet theory of the $2 daily trend were correct, there is only a 16% chance of rejecting the null. In other words, the study is quite weak.

When the power is small, failure to reject the null can reasonably be interpreted as a failure in the modeler (or in the data collection or in the experiment). The study has given very little information.

Just because the power is small is no reason to doubt the null hypothesis. Instead, you should think about how to conduct a better, more powerful study.

One way a study can be made more powerful is to increase the sample size. Fortunately, it’s feasible to figure out how large the study should be to achieve a given power. The reason is that the power depends on the two hypotheses: the null and the alternative. In carrying out the simulations using the null and alternative hypotheses, it’s possible to generate any desired amount of simulated data. It turns out that reliably detecting - a power of 80% - a $2 per day trend in stock prices requires about 75 years worth of data. This long historical period is probably not relevant to today’s investor. Indeed, it’s just about all the data that is actually available: the DJIA was started in 1928.

When the power is small for realistic amounts of data, the phenomenon you are seeking to find may be undetectable.

13.8 A Glossary of Hypothesis Testing

• Null Hypothesis : A statement about the world that you are interested to disprove. The null is almost always something that is clearly relevant and not controversial: that the conventional wisdom is true or that there is no relationship between variables. Examples: “The drug has no influence on blood pressure.” “Smaller classes do not improve school performance.”

The allowed outcomes of the hypothesis test relate only to the null:

• Reject the null hypothesis.
• Fail to reject the null hypothesis.

Alternative Hypothesis : A statement about the world that motivates your study and stands in contrast to the null hypothesis. “The drug will reduce blood pressure by 5 mmHg on average.” So, one possible alternative hypothesis is that “Decreasing class size from 30 to 25 will improve test scores by 3%.”

The outcome of the hypothesis test is not informative about the alternative. The importance of the alternative is in setting up the study: choosing a relevant test statistic and collecting enough data.

Test Statistic : The number that you use to summarize your study. This might be the sample mean, a model coefficient, or some other number. Later chapters will give several examples of test statistics that are particularly appropriate for modeling.

Type I Error : A wrong outcome of the hypothesis test of a particular type. Suppose the null hypothesis were really true. If you rejected it, this would be an error: a type I error.

Type II Error : A wrong outcome of a different sort. Suppose the alternative hypothesis were really true. In this situation, failing to reject the null would be an error: a type II error.

Significance Level :

A conditional probability. In the world where the null hypothesis is true, the significance is the probability of making a type I error. Typically, hypothesis tests are set up so that the significance level will be less than 1 in 20, that is, less than 0.05. One of the things that makes hypothesis testing confusing is that you do not know whether the null hypothesis is correct; it is merely assumed to be correct for the purposes of the deductive phase of the test. So you can’t say what is the probability of a type I error. Instead, the significance level is the probability of a type I error assuming that the null hypothesis is correct.

Ideally, the significance level would be zero. In practice, one accepts the risk of making a type I error in order to reduce the risk of making a type II error.

• p-value : This is the usual way of presenting the result of the hypothesis test. It is a number that summarizes how atypical the observed value of the test statistic would be in a world where the null hypothesis is true. The convention for rejecting the null hypothesis is p < 0.05.

The p-value is closely related to the significance level. It is sometimes called the achieved significance level .

• Power : This is a conditional probability. But unlike the significance, the condition is that the alternative hypothesis is true. The power is the probability that, in the world where the alternative is true, you will reject the null. Ideally, the power should be 100%, so that if the alternative really were true the null hypothesis would certainly be rejected. In practice, the power is less than this and sometimes much less.

In science, there is an accepted threshold for the p-value: \(0.05\) . But, somewhat strangely, there is no standard threshold for the power. When you see a study which failed to reject the null, it is helpful to know what the power of the study was. If the power was small, then failing to reject the null is not informative.

13.9 Update on Stock Prices

Figure 13.1 shows stock prices over the 10-year period from Dec. 5, 1997 to Nov. 14, 2007. For comparison, Figure 13.4 shows a wider time period, the 25-year period from 1985 to the month this section is being written in 2011.

When the first edition of this book was being written, in 2007, the 10-year period was a natural sounding interval, but a bit more information on the choice can help to illuminate a potential problem with hypothesis testing. I wanted to include a stock-price example because there is such a strong disconnection between the theories of stock prices espoused by professional economists - daily changes are a random walk - and the stories presented in the news, which wrongly provide a specific daily cause for each small change and see “bulls” and “bears” behind month- and year-long trends. I originally planned a time frame of 5 years - a nice round number. But the graph of stock prices from late 2002 to late 2007 shows a pretty steady upward trend, something that’s visually inconsistent with the random-walk null hypothesis. I therefore changed my plan, and included 10-years worth of data. If I had waited another year, through the 2008 stock market crash, the upward trend would have been eliminated. In 2010 and early 2011, the market climbed up again, only to fall dramatically in mid-summer.

That change from 5 to 10 years was inconsistent with the logic of hypothesis testing. I was, in effect, changing my data - by selecting the start and end points - to make them more consistent with the claim I wanted to make. This is always a strong temptation, and one that ought to be resisted or, at least, honestly accounted for.

Figure 13.4: Closing prices of the Dow Jones Industrial Average for the 25 years before July 9, 2011, the date on which the plot was made. The sub-interval used in this book’s first edition is shaded.

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons
• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

7.1: Logic and Purpose of Hypothesis Testing

• Last updated
• Save as PDF
• Page ID 7113

• Foster et al.
• University of Missouri-St. Louis, Rice University, & University of Houston, Downtown Campus via University of Missouri’s Affordable and Open Access Educational Resources Initiative

The statistician R. Fisher explained the concept of hypothesis testing with a story of a lady tasting tea. Here we will present an example based on James Bond who insisted that martinis should be shaken rather than stirred. Let's consider a hypothetical experiment to determine whether Mr. Bond can tell the difference between a shaken and a stirred martini. Suppose we gave Mr. Bond a series of 16 taste tests. In each test, we flipped a fair coin to determine whether to stir or shake the martini. Then we presented the martini to Mr. Bond and asked him to decide whether it was shaken or stirred. Let's say Mr. Bond was correct on 13 of the 16 taste tests. Does this prove that Mr. Bond has at least some ability to tell whether the martini was shaken or stirred?

This result does not prove that he does; it could be he was just lucky and guessed right 13 out of 16 times. But how plausible is the explanation that he was just lucky? To assess its plausibility, we determine the probability that someone who was just guessing would be correct 13/16 times or more. This probability can be computed to be 0.0106. This is a pretty low probability, and therefore someone would have to be very lucky to be correct 13 or more times out of 16 if they were just guessing. So either Mr. Bond was very lucky, or he can tell whether the drink was shaken or stirred. The hypothesis that he was guessing is not proven false, but considerable doubt is cast on it. Therefore, there is strong evidence that Mr. Bond can tell whether a drink was shaken or stirred.

Let's consider another example. The case study Physicians' Reactions sought to determine whether physicians spend less time with obese patients. Physicians were sampled randomly and each was shown a chart of a patient complaining of a migraine headache. They were then asked to estimate how long they would spend with the patient. The charts were identical except that for half the charts, the patient was obese and for the other half, the patient was of average weight. The chart a particular physician viewed was determined randomly. Thirty-three physicians viewed charts of average-weight patients and 38 physicians viewed charts of obese patients.

The mean time physicians reported that they would spend with obese patients was 24.7 minutes as compared to a mean of 31.4 minutes for normal-weight patients. How might this difference between means have occurred? One possibility is that physicians were influenced by the weight of the patients. On the other hand, perhaps by chance, the physicians who viewed charts of the obese patients tend to see patients for less time than the other physicians. Random assignment of charts does not ensure that the groups will be equal in all respects other than the chart they viewed. In fact, it is certain the groups differed in many ways by chance. The two groups could not have exactly the same mean age (if measured precisely enough such as in days). Perhaps a physician's age affects how long physicians see patients. There are innumerable differences between the groups that could affect how long they view patients. With this in mind, is it plausible that these chance differences are responsible for the difference in times?

To assess the plausibility of the hypothesis that the difference in mean times is due to chance, we compute the probability of getting a difference as large or larger than the observed difference (31.4 - 24.7 = 6.7 minutes) if the difference were, in fact, due solely to chance. Using methods presented in later chapters, this probability can be computed to be 0.0057. Since this is such a low probability, we have confidence that the difference in times is due to the patient's weight and is not due to chance.

Module 8: Inference for One Proportion

Hypothesis testing (2 of 5), learning outcomes.

• Recognize the logic behind a hypothesis test and how it relates to the P-value.

In this section, our focus is hypothesis testing, which is part of inference. On the previous page, we practiced stating null and alternative hypotheses from a research question. Forming the hypotheses is the first step in a hypothesis test. Here are the general steps in the process of hypothesis testing. We will see that hypothesis testing is related to the thinking we did in Linking Probability to Statistical Inference .

Step 1: Determine the hypotheses.

The hypotheses come from the research question.

Step 2: Collect the data.

Ideally, we select a random sample from the population. The data comes from this sample. We calculate a statistic (a mean or a proportion) to summarize the data.

Step 3: Assess the evidence.

Assume that the null hypothesis is true. Could the data come from the population described by the null hypothesis? Use simulation or a mathematical model to examine the results from random samples selected from the population described by the null hypothesis. Figure out if results similar to the data are likely or unlikely. Note that the wording “likely or unlikely” implies that this step requires some kind of probability calculation.

Step 4: State a conclusion.

We use what we find in the previous step to make a decision. This step requires us to think in the following way. Remember that we assume that the null hypothesis is true. Then one of two outcomes can occur:

• One possibility is that results similar to the actual sample are extremely unlikely. This means that the data do not fit in with results from random samples selected from the population described by the null hypothesis. In this case, it is unlikely that the data came from this population, so we view this as strong evidence against the null hypothesis. We reject the null hypothesis in favor of the alternative hypothesis.
• The other possibility is that results similar to the actual sample are fairly likely (not unusual). This means that the data fit in with typical results from random samples selected from the population described by the null hypothesis. In this case, we do not have evidence against the null hypothesis, so we cannot reject it in favor of the alternative hypothesis.

Data Use on Smart Phones

According to an article by Andrew Berg (“Report: Teens Texting More, Using More Data,” Wireless Week , October 15, 2010), Nielsen Company analyzed cell phone usage for different age groups using cell phone bills and surveys. Nielsen found significant growth in data usage, particularly among teens, stating that “94 percent of teen subscribers self-identify as advanced data users, turning to their cellphones for messaging, Internet, multimedia, gaming, and other activities like downloads.” The study found that the mean cell phone data usage was 62 MB among teens ages 13 to 17. A researcher is curious whether cell phone data usage has increased for this age group since the original study was conducted. She plans to conduct a hypothesis test.

The null hypothesis is often a statement of “no change,” so the null hypothesis will state that there is no change in the mean cell phone data usage for this age group since the original study. In this case, the alternative hypothesis is that the mean has increased from 62 MB.

• H 0 : The mean data usage for teens with smart phones is still 62 MB.
• H a : The mean data usage for teens with smart phones is greater than 62 MB.

The next step is to obtain a sample and collect data that will allow the researcher to test the hypotheses. The sample must be representative of the population and, ideally, should be a random sample. In this case, the researcher must randomly sample teens who use smart phones.

For the purposes of this example, imagine that the researcher randomly samples 50 teens who use smart phones. She finds that the mean data usage for these teens was 75 MB with a standard deviation of 45 MB. Since it is greater than 62 MB, this sample mean provides some evidence in favor of the alternative hypothesis. But the researcher anticipates that samples will vary when the null hypothesis is true. So how much of a difference will make her doubt the null hypothesis? Does she have evidence strong enough to reject the null hypothesis?

To assess the evidence, the researcher needs to know how much variability to expect in random samples when the null hypothesis is true. She begins with the assumption that H 0 is true – in this case, that the mean data usage for teens is still 62 MB. She then determines how unusual the results of the sample are: If the mean for all teens with smart phones actually is 62 MB, what is the chance that a random sample of 50 teens will have a sample mean of 75 MB or higher? Obviously, this probability depends on how much variability there is in random samples of this size from this population.

The probability of observing a sample mean at least this high if the population mean is 62 MB is approximately 0.023 (later topics explain how to calculate this probability). The probability is quite small. It tells the researcher that if the population mean is actually 62 MB, a sample mean of 75 MB or higher will occur only about 2.3% of the time. This probability is called the P-value .

Note: The P-value is a conditional probability, discussed in the module Relationships in Categorical Data with Intro to Probability . The condition is the assumption that the null hypothesis is true.

Step 4: Conclusion.

The small P-value indicates that it is unlikely for a sample mean to be 75 MB or higher if the population has a mean of 62 MB. It is therefore unlikely that the data from these 50 teens came from a population with a mean of 62 MB. The evidence is strong enough to make the researcher doubt the null hypothesis, so she rejects the null hypothesis in favor of the alternative hypothesis. The researcher concludes that the mean data usage for teens with smart phones has increased since the original study. It is now greater than 62 MB. ( P = 0.023)

Notice that the P-value is included in the preceding conclusion, which is a common practice. It allows the reader to see the strength of the evidence used to draw the conclusion.

How Small Does the P-Value Have to Be to Reject the Null Hypothesis?

A small P-value indicates that it is unlikely that the actual sample data came from the population described by the null hypothesis. More specifically, a small P-value says that there is only a small chance that we will randomly select a sample with results at least as extreme as the data if H 0 is true. The smaller the P-value, the stronger the evidence against H 0 .

But how small does the P-value have to be in order to reject H 0 ?

In practice, we often compare the P-value to 0.05. We reject the null hypothesis in favor of the alternative if the P-value is less than (or equal to) 0.05.

Note: This means that sampling variability will produce results at least as extreme as the data 5% of the time. In other words, in the long run, 1 in 20 random samples will have results that suggest we should reject H 0 even when H 0 is true. This variability is just due to chance, but it is unusual enough that we are willing to say that results this rare suggest that H 0 is not true.

Statistical Significance: Another Way to Describe Unlikely Results

When the P-value is less than (or equal to) 0.05, we also say that the difference between the actual sample statistic and the assumed parameter value is statistically significant . In the previous example, the P-value is less than 0.05, so we say the difference between the sample mean (75 MB) and the assumed mean from the null hypothesis (62 MB) is statistically significant. You will also see this described as a significant difference . A significant difference is an observed difference that is too large to attribute to chance. In other words, it is a difference that is unlikely when we consider sampling variability alone. If the difference is statistically significant, we reject H 0 .

Other Observations about Stating Conclusions in a Hypothesis Test

In the example, the sample mean was greater than 62 MB. This fact alone does not suggest that the data supports the alternative hypothesis. We have to determine that the data is not only larger than 62 MB but larger than we would expect to see in a random sampling if the population mean is 62 MB. We therefore need to determine the P-value. If the sample mean was less than or equal to 62 MB, it would not support the alternative hypothesis. We don’t need to find a P-value in this case. The conclusion is clear without it.

We have to be very careful in how we state the conclusion. There are only two possibilities.

• We have enough evidence to reject the null hypothesis and support the alternative hypothesis.
• We do not have enough evidence to reject the null hypothesis, so there is not enough evidence to support the alternative hypothesis.

If the P-value in the previous example was greater than 0.05, then we would not have enough evidence to reject H 0 and accept H a . In this case our conclusion would be that “there is not enough evidence to show that the mean amount of data used by teens with smart phones has increased.” Notice that this conclusion answers the original research question. It focuses on the alternative hypothesis. It does not say “the null hypothesis is true.” We never accept the null hypothesis or state that it is true. When there is not enough evidence to reject H 0 , the conclusion will say, in essence, that “there is not enough evidence to support H a .” But of course we will state the conclusion in the specific context of the situation we are investigating.

We compared the P-value to 0.05 in the previous example. The number 0.05 is called the significance level for the test, because a P-value less than or equal to 0.05 is statistically significant (unlikely to have occurred solely by chance). The symbol we use for the significance level is α (the lowercase Greek letter alpha). We sometimes refer to the significance level as the α-level. We call this value the significance level because if the P-value is less than the significance level, we say the results of the test showed a significant difference.

If the P-value ≤ α, we reject the null hypothesis in favor of the alternative hypothesis.

If the P-value > α, we fail to reject the null hypothesis.

In practice, it is common to see 0.05 for the significance level. Occasionally, researchers use other significance levels. In particular, if rejecting H 0 will be controversial or expensive, we may require stronger evidence. In this case, a smaller significance level, such as 0.01, is used. As with the hypotheses, we should choose the significance level before collecting data. It is treated as an agreed-upon benchmark prior to conducting the hypothesis test. In this way, we can avoid arguments about the strength of the data. We will look more at how to choose the significance level later. On this page, we continue to use a significance level of 0.05.

First, work through the interactive exercise below to practice the four steps of hypothesis testing and related concepts and terms.

Next, let’s look at some exercises that focus on the P-value and its meaning. Then we’ll try some that cover the conclusion.

For many years, working full-time has meant working 40 hours per week. Nowadays, it seems that corporate employers expect their employees to work more than this amount. A researcher decides to investigate this hypothesis.

• H 0 : The average time full-time corporate employees work per week is 40 hours.
• H a : The average time full-time corporate employees work per week is more than 40 hours.

To substantiate his claim, the researcher randomly selects 250 corporate employees and finds that they work an average of 47 hours per week with a standard deviation of 3.2 hours.

According to the Centers for Disease Control (CDC), roughly 21.5% of all high school seniors in the United States have used marijuana. (The data were collected in 2002. The figure represents those who smoked during the month prior to the survey, so the actual figure might be higher.) A sociologist suspects that the rate among African American high school seniors is lower. In this case, then,

• H 0 : The rate of African American high-school seniors who have used marijuana is 21.5% (same as the overall rate of seniors).
• H a : The rate of African American high-school seniors who have used marijuana is lower than 21.5%.

To check his claim, the sociologist chooses a random sample of 375 African American high school seniors and finds that 16.5% of them have used marijuana.

Contribute!

Improve this page Learn More

• Interactive: Concepts in Statistics - Hypothesis Testing (2 of 5). Authored by : Deborah Devlin and Lumen Learning. Located at : https://lumenlearning.h5p.com/content/1291194018762009888 . License : CC BY: Attribution
• Concepts in Statistics. Provided by : Open Learning Initiative. Located at : http://oli.cmu.edu . License : CC BY: Attribution

Notes on Topic 8: Hypothesis Testing

The logic of hypothesis testing.

The Logic of Hypothesis Testing As just stated, the logic of hypothesis testing in statistics involves four steps. State the Hypothesis : We state a hypothesis (guess) about a population. Usually the hypothesis concerns the value of a population parameter. Define the Decision Method : We define a method to make a decision about the hypothesis. The method involves sample data. Gather Data : We obtain a random sample from the population. Make a Decision : We compare the sample data with the hypothesis about the population. Usually we compare the value of a statistic computed from the sample data with the hypothesized value of the population parameter. If the data are consistent with the hypothesis we conclude that the hypothesis is reasonable. NOTE: We do not conclude it is right, but reasonable! AND: We actually do this by rejecting the opposite hypothesis (called the NULL hypothesis). More on this later. If there is a big discrepency between the data and the hypothesis we conclude that the hypothesis was wrong. We expand on those steps in this section: First Step: State the Hypothesis Stating the hypothesis actually involves stating two opposing hypotheses about the value of a population parameter. Example : Suppose we have are interested in the effect of prenatal exposure of alcohol on the birth weight of rats. Also, suppose that we know that the mean birth weight of the population of untreated lab rats is 18 grams. Here are the two opposing hypotheses: The Null Hypothesis (Ho). This hypothesis states that the treatment has no effect . For our example, we formally state: The null hypothesis (Ho) is that prenatal exposure to alcohol has no effect on the birth weight for the population of lab rats. The birthweight will be equal to 18 grams. This is denoted The Alternative Hypothesis (H1). This hypothesis states that the treatment does have an effect . For our example, we formally state: The alternative hypothesis (H1) is that prenatal exposure to alcohol has an effect on the birth weight for the population of lab rats. The birthweight will be different than 18 grams. This is denoted Second Step: Define the Decision Method We must define a method that lets us decide whether the sample mean is different from the hypothesized population mean. The method will let us conclude whether (reject null hypothesis) or not (accept null hypothesis) the treatment (prenatal alcohol) has an effect (on birth weight). We will go into details later. Third Step: Gather Data. Now we gather data. We do this by obtaining a random sample from the population. Example : A random sample of rats receives daily doses of alcohol during pregnancy. At birth, we measure the weight of the sample of newborn rats. The weights, in grams, are shown in the table. We calculate the mean birth weight. Experiment 1 Sample Mean = 13

Fourth Step: Make a Decision

An official website of the United States government

The .gov means it’s official. Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

The site is secure. The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

• Publications
• Account settings

Preview improvements coming to the PMC website in October 2024. Learn More or Try it out now .

• Advanced Search
• Journal List
• Educ Psychol Meas
• v.77(4); 2017 Aug

Hypothesis Testing in the Real World

Jeff miller.

1 University of Otago, Dunedin, New Zealand

Critics of null hypothesis significance testing suggest that (a) its basic logic is invalid and (b) it addresses a question that is of no interest. In contrast to (a), I argue that the underlying logic of hypothesis testing is actually extremely straightforward and compelling. To substantiate that, I present examples showing that hypothesis testing logic is routinely used in everyday life. These same examples also refute (b) by showing circumstances in which the logic of hypothesis testing addresses a question of prime interest. Null hypothesis significance testing may sometimes be misunderstood or misapplied, but these problems should be addressed by improved education.

One important goal of statistical analysis is to find real patterns in data. This is difficult when the data are subject to random noise, because random noise can produce illusory patterns “just by chance.” Given the difficulty of separating real patterns from coincidental ones within noisy data, it is important for researchers to use all of the appropriate tools and models to make inferences from their data (e.g., Gigerenzer & Marewski, 2015 ).

Null hypothesis significance testing (NHST) is one of the most commonly used types of statistical analysis, but it has been criticized severely (e.g., Kline, 2004 ; Ziliak & McCloskey, 2008 ). According to Cohen (1994) , for example, “NHST has not only failed to support the advance of psychology as a science but also has seriously impeded it” (p. 997). There have been calls for it to be supplemented with other types of analysis (e.g., Wilkinson & the Task Force on Statistical Inference, 1999 ), and at least one journal has banned its use outright ( Trafimow & Marks, 2015 ).

This note reviews the basic logic of NHST and responds to some criticisms of it. I argue that the basic logic is straightforward and compelling—so much so that it is commonly used in everyday reasoning. It is suitable for answering certain types of research questions, and of course it can be supplemented with additional techniques to address other questions. Criticisms of NHST’s logic either distort it or implicitly deny the possibility of ever finding patterns in data. The major problem with NHST is that some aspects of the method can be misunderstood, but the solution to that problem is to improve education—not to adopt new methods that address a different set of questions but are incapable of answering the question addressed by NHST. I conclude that it would be a mistake to throw out NHST.

The Common Sense Logic of NHST

Critics of NHST assert that it uses arcane, twisted, and ultimately flawed probabilistic logic (e.g., Cohen, 1994 ; Hubbard & Lindsay, 2008 ). To the contrary, the heart of NHST is a simple, intuitive, and familiar “common sense” logic that most people routinely use when they are trying to decide whether something they observe might have happened by coincidence (a.k.a., “randomly,” “by accident,” or “by chance”).

For example, suppose that you and five colleagues attend a departmental picnic. An hour after eating, three of you start to feel queasy. It comes out in discussion that those feeling queasy ate potato salad and that those not feeling queasy did not eat the potato salad. What could be more natural than to conclude that there was something wrong with the potato salad?

It is important to realize that this nonstatistical example fully embodies the underlying logic of hypothesis testing. First, a pattern is observed. In this example, the pattern is that people who ate potato salad felt queasy. Second, it is acknowledged that the pattern might have arisen just by chance. In this example, for instance, exactly those people who ate the potato salad—and no one else—might coincidentally all have been coming down with the flu, and the flu might have caused their queasiness. Third, there is reason to believe that the observed coincidence—while possible—would be very unlikely. In the example, real-world experience suggests that coming down with flu is a rare event, so it would be quite unlikely for several people to do so at just the same time, and it would of course be even more unlikely that those were exactly the people who ate the potato salad. Fourth, it is concluded that the observed pattern did not arise by chance. In this example, the “not by chance” conclusion suggests that there was something wrong with the potato salad.

To further clarify the analogy between NHST and the potato salad example, consider how a standard coin-flipping “statistical” data analysis situation could be described in parallel terms. Suppose a coin is flipped 50 times and it comes up heads 48 of them (pattern). This quite strong pattern could happen by coincidence, but elementary probability theory says that such a coincidence would be extremely unlikely. It therefore seems reasonable to conclude that the pattern was not just a coincidence; instead, the coin appears to be biased to come up heads. This is exactly the same line of reasoning used in the potato salad example: The observed pattern would be very unlikely to occur by chance, so it is reasonable to conclude that it arose for some other reason.

There are many other nonstatistical examples of the reasoning used in NHST. For instance, if you see an unusually large number of cars parked on the street where you live (pattern), you will probably conclude that something special is going on nearby. It is logically possible for all those cars to be there at the same time just by coincidence, but you know from your experience that this would be unlikely, so you reject the “just by chance” idea. Analogously, if two statistics students make an identical series of calculation errors on a homework problem (pattern), their instructor might well conclude that they had not done the homework independently. Although it is logically possible that the two students made the same errors by chance, that would seem so unlikely—at least for some types of errors—that the instructor would reject that explanation. These and many similar examples show that people often use the logic of hypothesis testing in the real world; essentially, they do so every time they conclude “that could not just be a coincidence.” Statistical hypothesis testing differs only in that laws of probability—rather than every-day experiences with various coincidences—are used to assess the likelihood that an observed pattern would occur by chance.

Criticisms of NHST’s Logic

According to Berkson (1942) , “There is no logical warrant for considering an event known to occur in a given hypothesis, even if infrequently, as disproving the hypothesis” (p. 326). In terms of our examples, Berkson is saying that it is illogical to consider 3/6 queasy friends as proving that there was something wrong with the potato salad, because it could be just a coincidence. Taken to its logical extreme, his statement implies that observing 48/50 heads should also not be regarded as disproving the hypothesis of a fair coin, because that too could happen by chance. To be sure, Berkson is mathematically correct that the suggested conclusions about the quality of the potato salad and the fairness of the coin do not follow from the observed patterns with the same 100% certainty that implications have in propositional logic (e.g., modus ponens ). On the other hand, it is unrealistic to demand that level of certainty before reaching conclusions from noisy data, because such data will almost never support any interesting conclusions with 100% certainty. In practice, 48/50 heads seems like ample evidence to conclude—with no further assumptions—that a coin must be biased, and the “logical” objection that this could have happened by chance seems rather intransigent. Given that logical certainty is unattainable due to the presence of noise in the data, one can only consider the probabilities of various correct and incorrect decisions (e.g., Type I error rates, power) under various hypothesized conditions, which is exactly what NHST does.

Another long-standing objection to NHST is that its conclusions depend on the probabilities of events that did not actually occur (e.g., Cox, 1958 ; Wagenmakers, 2007 ). For example, in deciding whether 3/6 people feeling queasy was too much of a coincidence, people might be influenced by how often they had seen 4/6, 5/6, or 6/6 people in a group feel queasy by chance, even though only 3/6 had actually been observed. It is difficult to see much practical force to this objection, however. In trying to decide whether a particular pattern is too strong to be observed by chance, it seems quite relevant to consider all of the different patterns that might be observed by chance—especially the patterns that are even stronger. Proponents of this objection generally support it with artificial probability distributions in which stronger patterns are at least as likely to occur by chance as weaker patterns, but such distributions rarely if ever arise in actual research scenarios.

Critics of NHST sometimes claim that its logical form is parallel to that of the argument shown in Table 1 (e.g., Cohen, 1994 ; Pollard & Richardson, 1987 ). There is obviously something wrong with the argument in this table, and NHST must be flawed if it uses the same logic. This criticism is unfounded, however, because the logic illustrated in Table 1 is not parallel to that of NHST.

A Misleading Caricature of Null Hypothesis Significance Testing’s Logical Form.

The argument given in Table 1 suggests that a null hypothesis—in this case, that a person is an American—should be rejected whenever the observed results are unlikely under that hypothesis. NHST requires more than that, however. Implicitly, in order to reject a null hypothesis, NHST requires that the observed results must be more likely under an alternative hypothesis than under the null. In the potato salad example, for instance, rejecting the coincidence explanation requires not only that the observed pattern is unlikely by chance when the potato salad is good, but also that this pattern is more likely when the potato salad is bad (i.e., more likely when the null hypothesis is false than when it is true).

Figure 1 shows how this additional requirement arises within NHST using the Z test as an example. The null hypothesis predicts that the outcome is a draw from the depicted standard normal distribution, and Region A (i.e., the cross-hatched tails) of this distribution represent the Z values for which the null would be rejected at p < .05. Critically, Region B in the middle of the distribution also depicts an area of 5%. If NHST really only required that the rejection region had a probability of 5% under the null hypothesis, as implied by the argument in Table 1 , then rejecting the null for an observation in Region B would be just as appropriate as rejecting it for an observation in Region A. This is not all that NHST requires, however, and in fact outcomes in Region B would not be considered evidence against the null hypothesis. The null hypothesis is rejected for outcomes in A but not for those in B, because of the requirement that an outcome in the rejection region must have higher probability when the null hypothesis is false than when it is true. Region B of Figure 1 clearly does not satisfy this additional requirement, because this area will have a higher probability when the null hypothesis is true than when it is not.

A standard normal ( Z ) distribution of observed scores under the null hypothesis.

Note . Region A: The two cross-hatched areas indicate the standard two-tailed rejection region—that is, the 5% of the distribution most discrepant from the mean. Region B: The dark shaded area in the middle of the distribution also represents an area of 5%. Under NHST, only observations in the tails are taken as evidence that the null hypothesis should be rejected, even though the probability of an observation in Region B is just as low (i.e., 5%).

Likewise, the example of Table 1 clearly does not satisfy the additional requirement that the observed results should be more likely under some alternative to the null hypothesis. The probability that a person is a member of Congress is lower—not higher—if the person is not an American. In fact, the logic of NHST actually requires a first premise of the form:

• 1′. If a person is an American, then he is probably not a member of Congress; on the other hand, if he is not an American, then he is more likely to be a member of Congress.

Premise 1′ is obviously false, so the conclusion (3) is obviously not supported within NHST.

Finally, critics of NHST often complain that its conclusions can depend on the sampling methods used to collect the data as well as on the data themselves (e.g., Wagenmakers, 2007 ). This dependence arises because NHST’s assessment of “how likely is such an extreme pattern by chance” depends on the exact probabilities of various outcomes, and these in turn depend on the details of how the sampling was carried out. This is thought to be a problem for NHST, because—according to critics—the conclusion from a data set should depend only on what the data are, but not on the sampling plan used to collect them. This argument begs the question, however. Of course, the assessment of what will happen “by chance” can only be done within a well-defined set of possible outcomes. These outcomes are necessarily determined by the sampling plan, so the plan must influence the assessment of the various patterns’ probabilities. Viewed in this manner, it seems quite reasonable that any conclusion about the presence of an unusual pattern would depend on the sampling plan as well as on the observations themselves.

Ancillary Criticisms of NHST

Additional criticisms have been directed at aspects of NHST other than its logic. For example, it is sometimes claimed that NHST does not address the question of main interest. Critics often assert that researchers “really” want to know the probability that a pattern is coincidental given the data (e.g., Berger & Berry, 1988 ; Cohen, 1994 ; Kline, 2004 ). Within the current examples, then, the claim is that people really want to know “the probability that these 3/6 picnic-goers feel sick by coincidence” or “the probability that the coin is biased towards heads.”

It is clear that NHST does not provide such probabilities, but it is not so clear that everyone always wants them. In many cases, people simply want to decide whether the pure chance explanation is tenable; for example, it is difficult to imagine a picnic-goer asking for a precise probability that the potato salad was bad. In any case, to obtain such probabilities requires knowing all of the other possible explanations, plus their prior probabilities (e.g., Efron, 2013 ). In many situations where NHST is used, the complete set of other possible explanations and their probabilities are simply unknown. In these situations, no statistical method can compute the probability that researchers supposedly want, and it seems unfair to criticize NHST for failing to provide something that cannot be determined with any other technique either.

Surely the most frequent and justified criticisms of NHST revolve around the idea that researchers do not completely understand it (e.g., Batanero, 2000 ; Wainer & Robinson, 2003 ). A number of findings suggest that one aspect of NHST in particular—the so-called “ p value”—is widely misunderstood (e.g., Gelman, 2013 ; Haller & Kraus, 2002 ; Hubbard & Lindsay, 2008 ; Kline, 2004 ). Explicitly or implicitly, such findings are taken as evidence that NHST should be abandoned because it is too difficult to use properly (e.g., Cohen, 1994 ).

Unfortunately, similar data suggest that many other concepts in probability and statistics are also poorly understood (e.g., Campbell, 1974 ). If we abandon all methods based on misunderstood statistical concepts, then almost all statistically based methods will have to go, including some apparently quite practical and important ones (e.g., diagnostic testing in medicine; Gigerenzer, Gaissmaier, Kurz-Milcke, Schwartz, & Woloshin, 2008 ). Within this difficult context, there seems to be no reason to abandon NHST selectively, because there is “no evidence that NHST is misused any more often than any other procedure” ( Wainer & Robinson, 2003 , p. 22). Moreover, if one accepted the argument that all poorly understood methods should be abandoned, then some useful but poorly understood nonstatistical methods would presumably also have to go (e.g., propositional logic; Rips & Marcus, 1977 ; Wason, 1968 ). Surely it would be a mistake to abandon a valuable tool or technique simply because considerable training and effort are required to use it correctly.

The current discussion of frequent false positives and low replicability in research areas using NHST (e.g., Francis, 2012 ; Nosek, Spies, & Motyl, 2012 ; Simmons, Nelson, & Simonsohn, 2011 ) also suggests that there are misunderstandings and misuse of this technique. Specifically, there is evidence that researchers capitalize on flexibility in the selection of their data and in the application of their analyses (i.e., “ p -hacking”) in order to obtain statistically significant and therefore publishable results (e.g., Bakker, Van Dijk, & Wicherts, 2012 ; John, Loewenstein, & Prelec, 2012 ; Tsilidis et al., 2013 ). Such practices are a misuse of NHST, and they inflate positive rates, especially in combination with existing biases toward publication of surprising new findings and with the relative scarcity of such findings within well-studied areas (e.g., Ferguson & Heene, 2012 ; Ioannidis, 2005 ). The false positive problem is not specific to NHST, however; it would arise analogously within any statistical framework. Whatever statistical methods are used to detect new patterns in noisy data, the rate of reporting imaginary patterns (i.e., false positives) will be inflated by flexibility in the selection of the data, flexibility in the application of the methods, and flexibility in the choice of what findings are reported.

To the extent that misunderstanding of NHST presents a problem, better education of researchers seems like the best path toward a solution (e.g., Holland, 2007 ; Kalinowski, Fidler, & Cumming, 2008 ; Leek & Peng, 2015 ). Although the underlying logic of NHST has considerable common sense appeal—as shown by the real-world examples described earlier—this logic is often obscured when the methods are taught to beginners. This is partly because of the specialized and unintuitive terminology that has been developed for NHST (e.g., “null hypothesis,” “Type I error,” “Type II error,” “power”). Another problem is that introductions to NHST nearly always focus primarily on the mathematical formulas used to compute the probabilities of observing various patterns by chance (i.e., “distributions under the null hypothesis”). Students can easily be so confused about the workings of these formulas that they fail to appreciate the simplicity of the underlying logic.

Conclusions

NHST is a useful heuristic for detecting nonrandom patterns, and abandoning it would be counterproductive. Its underlying logic—both in scientific research and in everyday life—is that chance can be rejected as an explanation of observed patterns that would rarely occur by coincidence. It is true that the conclusion of a biased coin does not follow with 100% certainty, and it will be wrong when an unlikely pattern really does occur by chance. Researchers should certainly keep this possibility in mind and resist the tendency to believe that every pattern documented statistically—whether by NHST or any other technique—necessarily reflects the true state of the world. As a practical strategy for detecting non-random patterns in a noisy world, however, it seems quite a reasonable heuristic to conclude tentatively that something other than chance is responsible for systematic observed patterns.

While NHST is extremely useful for deciding whether patterns might have arisen by chance, it is, of course, not the only useful statistical technique. In fact, when NHST is employed, “the answer to the significance test is rarely the only thing we should consider” ( Cox, 1958 , p. 367), so it is not sufficient for researchers to try to answer all research questions entirely within the NHST framework. For example, NHST is not appropriate for evaluating how strongly a data set supports a null hypothesis (e.g., Grant, 1962 ). For that purpose, it is better to use confidence intervals or Bayesian techniques (e.g., Cumming & Fidler, 2009 ; Rouder, Speckman, Sun, Morey, & Iverson, 2009 ; Wainer & Robinson, 2003 ; Wetzels, Raaijmakers, Jakab, & Wagenmakers, 2009 ). Fortunately, there is no fundamental limit on the number of statistical tools that researchers can use. Researchers should always use the set of tools most suitable for the questions under consideration. In many cases, that set will include NHST.

Acknowledgments

I thank Scott Brown, Patricia Haden, Wolf Schwarz, and two anonymous reviewers for constructive comments on earlier versions of the article.

Declaration of Conflicting Interests: The author(s) declared no potential conflicts of interest with respect to the research, authorship, and/or publication of this article.

Funding: The author(s) disclosed receipt of the following financial support for the research, authorship, and/or publication of this article: Preparation of this article was supported by a research award from the Alexander von Humboldt Foundation.

• Bakker M., Van Dijk A., Wicherts J. M. (2012). The rules of the game called psychological science . Perspectives on Psychological Science , 7 , 543-554. doi: 10.1177/1745691612459060 [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Batanero C. (2000). Controversies around the role of statistical tests in experimental research . Mathematical Thinking and Learning , 2 , 75-97. doi: 10.1207/S15327833MTL0202_4 [ CrossRef ] [ Google Scholar ]
• Berger J. O., Berry D. A. (1988). Statistical analysis and the illusion of objectivity . American Scientist , 76 , 159-165. [ Google Scholar ]
• Berkson J. (1942). Tests of significance considered as evidence . Journal of the American Statistical Association , 37 , 325-335. doi: 10.1080/01621459.1942.10501760 [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Campbell S. K. (1974). Flaws and fallacies in statistical thinking . Englewood Cliffs, NJ: Prentice-Hall. [ Google Scholar ]
• Cohen J. (1994). The earth is round ( p < .05) . American Psychologist , 49 , 997-1003. doi: 10.1037//0003-066X.49.12.997 [ CrossRef ] [ Google Scholar ]
• Cox D. R. (1958). Some problems connected with statistical inference . Annals of Mathematical Statistics , 29 , 357-372. doi: 10.1214/aoms/1177706618 [ CrossRef ] [ Google Scholar ]
• Cumming G., Fidler F. (2009). Confidence intervals: Better answers to better questions . Zeitschrift für Psychologie , 217 , 15-26. doi: 10.1027/0044-3409.217.1.15 [ CrossRef ] [ Google Scholar ]
• Efron B. (2013). Bayes’ theorem in the 21st century . Science , 340 , 1177-1178. doi: 10.1126/science.1236536 [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Ferguson C. J., Heene M. (2012). A vast graveyard of undead theories: Publication bias and psychological science’s aversion to the null . Perspectives on Psychological Science , 7 , 555-561. doi: 10.1177/1745691612459059 [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Francis G. (2012). Publication bias and the failure of replication in experimental psychology . Psychonomic Bulletin & Review , 19 , 975-991. doi: 10.3758/s13423-012-0322-y [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Gelman A. (2013). Commentary: P values and statistical practice . Epidemiology , 24 , 69-72. [ PubMed ] [ Google Scholar ]
• Gigerenzer G., Gaissmaier W., Kurz-Milcke E., Schwartz L. M., Woloshin S. (2008). Helping doctors and patients make sense of health statistics . Psychological Science in the Public Interest , 8 , 53-96. doi: 10.1111/j.1539-6053.2008.00033.x [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Gigerenzer G., Marewski J. N. (2015). Surrogate science: The idol of a universal method for scientific inference . Journal of Management , 41 , 421-440. doi: 10.1177/0149206314547522 [ CrossRef ] [ Google Scholar ]
• Grant D. A. (1962). Testing the null hypothesis and the strategy and tactics of investigating theoretical models . Psychological Review , 69 , 54-61. doi: 10.1037/h0038813 [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Haller H., Kraus S. (2002). Misinterpretations of significance: A problem students share with their teachers? Methods of Psychological Research , 7 , 1-20. [ Google Scholar ]
• Holland B. K. (2007). A classroom demonstration of hypothesis testing . Teaching Statistics , 29 , 71-73. doi: 10.1111/j.1467-9639.2007.00269.x [ CrossRef ] [ Google Scholar ]
• Hubbard R., Lindsay R. M. (2008). Why p values are not a useful measure of evidence in statistical significance testing . Theory & Psychology , 18 , 69-88. doi: 10.1177/0959354307086923 [ CrossRef ] [ Google Scholar ]
• Ioannidis J. P. A. (2005). Why most published research findings are false . PLoS Medicine , 2 ( 8 ), e124. doi: 10.1371/journal.pmed.0020124 [ PMC free article ] [ PubMed ] [ CrossRef ] [ Google Scholar ]
• John L. K., Loewenstein G., Prelec D. (2012). Measuring the prevalence of questionable research practices with incentives for truth-telling . Psychological Science , 23 , 524-532. doi: 10.1177/0956797611430953 [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Kalinowski P., Fidler F., Cumming G. (2008). Overcoming the inverse probability fallacy: A comparison of two teaching interventions . Methodology: European Journal of Research Methods for the Behavioral and Social Sciences , 4 , 152-158. [ Google Scholar ]
• Kline R. B. (2004). Beyond significance testing: Reforming data analysis methods in behavioral research . Washington, DC: American Psychological Association. [ Google Scholar ]
• Leek J. T., Peng R. D. (2015). P values are just the tip of the iceberg . Nature , 520 , 612. [ PubMed ] [ Google Scholar ]
• Nosek B. A., Spies J. R., Motyl M. (2012). Scientific utopia II. Restructuring incentives and practices to promote truth over publishability . Perspectives on Psychological Science , 7 , 615-631. [ Google Scholar ]
• Pollard P., Richardson J. T. E. (1987). On the probability of making Type I errors . Psychological Bulletin , 102 , 159-163. doi: 10.1037/0033-2909.102.1.159 [ CrossRef ] [ Google Scholar ]
• Rips L. J., Marcus S. L. (1977). Suppositions and the analysis of conditional sentences . In Just M. A., Carpenter P. A. (Eds.), Cognitive processes in comprehension (pp. 185-220). Hillsdale, NJ: Lawrence Erlbaum. [ Google Scholar ]
• Rouder J. N., Speckman P. L., Sun D., Morey R. D., Iverson G. (2009). Bayesian t tests for accepting and rejecting the null hypothesis . Psychonomic Bulletin & Review , 16 , 225-237. doi: 10.3758/PBR.16.2.225 [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Simmons J. P., Nelson L. D., Simonsohn U. (2011). False-positive psychology: Undisclosed flexibility in data collection and analysis allows presenting anything as significant . Psychological Science , 22 , 1359-1366. doi: 10.1177/0956797611417632 [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Trafimow D., Marks M. (2015). Editorial . Basic and Applied Social Psychology , 37 ( 1 ), 1-2. doi: 10.1080/01973533.2015.1012991 [ CrossRef ] [ Google Scholar ]
• Tsilidis K. K., Panagiotou O. A., Sena E. S., Aretouli E., Evangelou E., Howells D. W., … Ioannidis J. P. A. (2013). Evaluation of excess significance bias in animal studies of neurological diseases . PLoS Biology , 11 ( 7 ), e1001609. doi: 10.1371/journal.pbio.1001609 [ PMC free article ] [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Wagenmakers E. J. (2007). A practical solution to the pervasive problems of p values . Psychonomic Bulletin & Review , 14 , 779-804. [ PubMed ] [ Google Scholar ]
• Wainer H., Robinson D. H. (2003). Shaping up the practice of null hypothesis significance testing . Educational Researcher , 32 , 22-30. doi: 10.3102/0013189X032007022 [ CrossRef ] [ Google Scholar ]
• Wason P. C. (1968). Reasoning about a rule . Quarterly Journal of Experimental Psychology , 20 , 273-281. doi: 10.1080/14640746808400161 [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Wetzels R., Raaijmakers J. G. W., Jakab E., Wagenmakers E. J. (2009). How to quantify support for and against the null hypothesis: A flexible WinBUGS implementation of a default Bayesian t test . Psychonomic Bulletin & Review , 16 , 752-760. doi: 10.3758/PBR.16.4.752 [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Wilkinson L., & the Task Force on Statistical Inference. (1999). Statistical methods in psychology journals: Guidelines and explanations . American Psychologist , 54 , 594-604. doi: 10.1037/0003-066X.54.8.594 [ CrossRef ] [ Google Scholar ]
• Ziliak S. T., McCloskey D. (2008). The cult of statistical significance: How the standard error costs us jobs, justice, and lives . Ann Arbor: University of Michigan Press. [ Google Scholar ]

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons
• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

7.1: Logic and Purpose of Hypothesis Testing

• Last updated
• Save as PDF
• Page ID 195830