maths problem solving objectives

Math IEP Goals For Special Education

Drafting IEP goals can be difficult, so here are a few math IEP goals (across various ability levels) to get you started. Please adapt and modify to meet the specific needs of your students. Keep in mind a goal should be a skill you believe is achievable by the student in 1 school year. You can always do an addendum if a student has met all criteria for the goal/objectives.

Remember, when writing objectives, break down the goal into smaller steps. You can lessen the percentage of accuracy, the number of trials (3/5 vs 4/5), or amount of prompting. Just make sure the objectives build on each other and are working towards mastery.

The reason why I always list accuracy at 100% when writing Math goals is because the answer is either right or wrong, an answer to a math problem can’t be 50% correct. So feel free to play with the ## of trials for accuracy.

Number Identification:

Goal: Student will independently identify numbers 1-20 (verbally, written, or pointing) with 100% accuracy on 4 out of 5 trials measured quarterly.

Goal: When verbally prompted by teacher to “point to the number _________”, Student will independently select the correct number with 100% accuracy on 4 out of 5 trials measured quarterly.

Goal: Student will independently count in rote order numbers 1-25 with 100% accuracy on 4 out of 5 trials measured quarterly.

Goal: Student will independently count by 2, 3, 5, 10 starting from 0-30 verbally or written, with 100% accuracy on 4 out of 5 trials measured quarterly.

One-to-one Correspondence:

Goal: When given up to 10 objects, Student will independently count and determine how many objects there are (verbally, written, or by pointing to a number) with 100% accuracy on 4 out of 5 trials measured quarterly/monthly.

Goal: When given up to 10 items/objects, Student will independently count and move the items to demonstrate 1:1 correspondence and identify how many there are with 100% accuracy on 4 out of 5 trials measured quarterly.

Goal: Given 10 addition problems, Student will independently add single digit numbers with regrouping with 100% accuracy on 4 out of 5 trials as measured quarterly.

Goal:  Student will independently add a single digit number to a double digit number with and without regrouping with 100% accuracy on 4 out of 5 trials measured quarterly.

Goal: Student will independently add double digit numbers to double digit numbers with (or without) regrouping with 100% accuracy on 4 out of 5 trials measured quarterly.

Adding with Number Line:

Goal: Given 10 addition problems and using a number line, Student will independently add single digit numbers with 100% accuracy on 4 out of 5 trials measured quarterly. 

Subtraction:

Goal: Student will independently subtract a single digit number form a double digit number with and without regrouping with 100% accuracy on 4 out of 5 trials measured quarterly.

Goal: Given 10 subtraction problems, Student will independently subtract double digit numbers from double digit numbers with and without regrouping with 100% accuracy on 4 out of 5 trials measured quarterly.

Goal: Student will independently subtract money/price amounts from one another with and without regrouping, while carrying the decimal point with 100% accuracy on 4 out of 5 trials as measured quarterly.

Goal: Using a number line, Student will independently subtract numbers (20 or less) with 100% accuracy on 4 out of 5 trials measured quarterly.

Telling Time:

Goal: Student will independently tell time to the half hour on an analog clock (verbally or written) with 100% accuracy on 4 out of 5 trials measured quarterly. 

Goal: Student will independently tell time to the hour on an analog clock (verbally or written) with 100% accuracy on 4 out of 5 trials measured quarterly.

Elapsed Time:

Goal: Given a problem with a start time and end time, Student will independently determine how much time has elapsed with 100% accuracy on 4 out of 5 trials measured quarterly.

Goal: Given a problem with a start time and duration of activity/event, Student will independently determine what the end time is with 100% accuracy on 4 out of 5 trials measured quarterly.

Dollar More:

Goal: Using the dollar more strategy, Student will independently identify the next dollar up when given a price amount with 100% accuracy on 4 out of 5 trials measured quarterly.

Goal: Student will independently identify the next dollar amount when given a price, determine how much is needed to make the purchase, and count out the necessary amount (using fake school money) with 100% accuracy on 4 out of 5 trials measured quarterly.

Goal: When given a price, student will identify which number is the dollar amount with 100% accuracy on 4 out of 5 trials measured quarterly.      

Money Identification/Counting Money:

Goal: When given a quarter, dime, nickel, and penny, Student will identify the coin and corresponding value with 100% accuracy on 4 out of 5 trials measured quarterly.

Goal: When given a random amount of coins (all of one type), Student will independently count the coins with 100% accuracy on 4 out of 5 trials measured quarterly.

Goal: When given a mix of coins (to include quarter, dime, nickel, penny), Student will independently count the coins with 100% accuracy on 4 out of 5 trials measured quarterly.

Goal: When given a mixture of coins and dollar bills, Student will independently count the money with 100% accuracy on 4 out of 5 trials measured quarterly.

Goal: When give 2, 3, and 4 digit numbers, Student will independently round to the nearest tens, hundreds, thousands independently with 100% accuracy on 4 out of 5 trials measured quarterly.

Greater than/Less than:

Goal: Given 2 numbers, pictures, or groups of items, Student will independently determine which number is greater than/less than/equal by selecting or drawing the appropriate symbol (<,>, =) with 100% accuracy on 4 out of 5 trials measured quarterly.

Goal: Student will independently count objects or pictures of objects and tally the corresponding amount (up to 15) with 100% accuracy on 4 out of 5 trials as measured quarterly.

Goal: Given a number, up to 20, Student will independently tally the corresponding number with 100% accuracy on 4 out of 5 trials measured quarterly.

Goal: Given data and a bar graph template, Student will independently construct a bar graph to display the data and answer 3 questions about the data with 100% accuracy on 4 out of 5 trials measured quarterly.

Goal: Given a line, pie, or bar graph, Student will independently answer questions about each set of data with 100% accuracy on 4 out of 5 trials measured quarterly.

Goal: Given data and a blank graph template, Student will independently construct the graph to display the appropriate data with 100% accuracy on 4 out of 5 trials measured quarterly.

Goal: Student will independently identify the numerator and denominator in a fraction with 100% accuracy on 4 out of 5 trials measured quarterly.

Goal: When given a picture of a shape divided into parts, Student will independently color the correct sections in to represent the fraction given with 100% accuracy on 4 out of 5 trials measured quarterly.

Goal: Student will independently add fractions with like denominators with 100% accuracy on 4 out of 5 trials measured quarterly.

Word Problems:

Goal: Student will independently solve one step addition and subtraction word problems with 100% accuracy on 4 out of 5 trials measured quarterly.

Goal: Student will independently solve two step word problems (mixed addition and subtraction) with 100% accuracy on 4 out of 5 trials measured quarterly.

Goal: Student will independently solve one and two step multiplication world problems with 100% accuracy on 4 out of 5 trials measured quarterly.

Goal: Student will independently read a one or two step word problem, identify which operation is to be used, and solve it with 100% accuracy on 4 out of 5 trials measured quarterly.

Goal: Given a word problem, Student will independently determine which operation is to be used (+,-,x, /) with 100% accuracy on 4 out of 5 trials measured quarterly.

Even/Odd Numbers:

Goal: When given a number, student will independently identify if the number is odd or even (written or verbally), with 100% accuracy on 4 out of 5 trials measured quarterly.

Measurement:

Goal: Given varying lines and objects, Student will independently estimate the length of the object/picture, measure it using a ruler, and identify how long the object/picture is with 100% accuracy on 4 out of 5 trials measured quarterly.

Multiplication:

Goal: Student will independently solve 10 multiplication facts (2, 3, and 5 facts) with 100% accuracy on 4 out of 5 trials measured quarterly.

Goal: Student will independently solve 20 multiplication facts (facts up to 9) with 100% accuracy on 4 out of 5 trials measured quarterly.

Goal: Given a division problem (where the divisor is _____), Student will independently solve it with 100% accuracy on 4 out of 5 trials measured quarterly.

Feel free to use and edit as necessary. It’s up to you how often you want to measure the goals, but remind parents that even if the goal says 5/5 times quarterly, it doesn’t mean you’re only working on it those 5 times. That is just the number of times you’ll take official data. Just make sure it’s a reasonable ## so you have time to take all the data you need. Especially if you have multiple goals/objectives to take data for!

Happy drafting!

Where should we send your

Free lesson plans, success check your email for your free lessons.

We hate SPAM and promise to keep your email address safe.

Want some lesson plans you can immediately use?

Enter your email address below to get 5 free lesson plans now  .

Math teaching support you can trust

resources downloaded

one-on-one tutoring sessions

schools supported

[FREE] Fun Math Games & Activities

Engage your students with our ready-to-go packs of no-prep games and activities for a range of abilities across Kindergarten to Grade 5!

Developing Math Reasoning In Elementary School And Beyond: The Mathematical Skills Required And How To Teach Them

Developing math reasoning skills in elementary school is crucial to succeed in developing a math mastery approach to learning which will support development through to middle school and high school. Students need strong applied reasoning alongside their math skills to be able to succeed – there’s no point in memorizing a theorem if you don’t know when to use it!

The Ultimate Guide to Problem Solving Techniques

Help your students to develop their problem solving skills with this free worksheet.

My approach to elementary school level math teaching and learning is that it should be about exploring, reasoning and challenging thinking, rather than learning rote/abstract rules for calculations and facts.

Though I recognize that fluency in math and memorizing key number facts is essential in elementary school mathematics to acquire the basics – these are the prerequisite skills that ought to be used and applied in real life contexts.

To succeed on standardized tests, it is clear that children require deep knowledge of facts and mathematical concepts. Moreover, they need to be able to use and apply these facts to a range of contexts, and different types of word problems , including the more complex multi-step and two-step word problems

What is reasoning in math?

Let’s start with the definition of math reasoning. Reasoning in math is the process of applying logical and critical thinking to a mathematical problem in order to make connections to work out the correct strategy to use (and as importantly, not to use) in reaching a solution.

Reasoning is sometimes seen as the glue that bonds students’ mathematical skills together; it’s also seen as bridging the gap between fluency and problem solving, allowing students to use their fluency to accurately carry out problem solving.

In my opinion, it is only when we teach children to reason and give them the freedom to look for different strategies when faced with an unfamiliar context that we are really teaching mathematics in elementary school.

There are two different types of reasoning: inductive reasoning and deductive reasoning. 

Inductive reasoning is also called bottom-up logic. When using inductive reasoning, people come to a conclusion based on observations. However, their conclusion may or may not be factual. For example, a student may observe that the following set of numbers is divisible by 4: 12, 36, 40, 48. They also notice that each of the numbers in the set are even. Therefore, they conclude that all even numbers are divisible by 4. This, however, is false. 

Deductive reasoning is also called top-down logic and works the opposite way of inductive reasoning. When using deductive reasoning, people use known facts in order to reach a conclusion. For example, a student may be trying to determine if all even numbers are divisible by 4. They may use the examples 22 / 4 and 30 / 4 to prove that not all even numbers are divisible by 4. This makes deductive reasoning more reliable.

Why focus teaching and learning on reasoning?

Logical reasoning requires metacognition (thinking about thinking) . It influences behavior and attitudes through greater engagement, requesting appropriate help (self-regulation) and seeking conceptual understanding.

Reasoning promotes these traits because it requires children to use their mathematical vocabulary . In short, reasoning requires a lot of active talk.

It is worth mentioning that with reasoning, active listening is equally important and if done right can also ensure increased learning autonomy for students.

The theory behind mathematical reasoning in elementary school

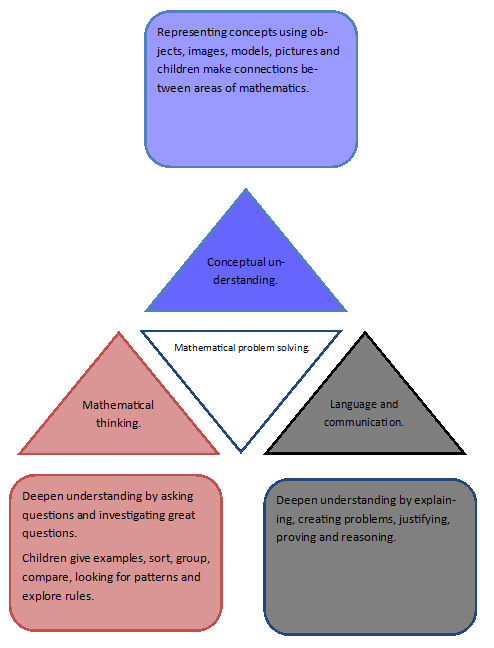
The infographic (below) from Helen Drury cleverly details what should underpin a mathematics teaching and learning syllabus. It’s a good starting point when you’re thinking about your mathematics curriculum in the context of fluency reasoning and problem solving .

I’ve also been very influenced by the Five Principles of Extraordinary Math Teaching by Dan Finkel

These are as follows, and are a great starting point to developing math reasoning at the elementary school level

1. Start math lessons with a question

2. Students need to wonder and struggle

3. You are not the answer key

4. Say yes to your students original ideas (but not yes to methodical answers)

See also this free guide to elementary math problem solving and reasoning techniques .

How to make reasoning central to math lessons in elementary school

Pose lesson objectives as questions to elementary school children..

A  ‘light bulb’ idea from my own teaching and learning was to redesign learning objectives, fashioning them into a question for learning. Instead of ‘to identify multiples of a number’, for example, I’ll use ‘why is a square number a square number?’. Another example is: instead of ‘to use ratio to describe the relationship between two quantities,’ we can ask students ‘in a recipe, if the ratio of sugar to flour is 3:5, what does that mean?’

Phrasing LOs as a question instantly engages and enthuses children, they wonder what the answer is. It also ensures that they show their reasoning in a model or image when they answer.

In this instance – interestingly – children knew the process to calculate square numbers but could not articulate or mathematically reason why it worked until after the session.

It seems denying children answers allows them time to use their thinking skills, struggle and learn.

Ban the word ‘yes’ in math lessons

One of the simplest strategies I have found to make reasoning inseparable from mathematical learning is to ban the word ‘yes’ from the classroom.

Instead, asking children to reason their thoughts and explain why they think they are right can allow for greater learning gains and depth of understanding. Admittedly, this is still a work in progress and easier said than done.

To facilitate this, I always tell my children that I am not the answer key.

Using my example of square numbers, I allowed children time to struggle and wrestle with my question without providing an answer or giving hints. Instead, I questioned the students to unpack understanding at the beginning of the lesson and brought together mathematical ideas during a whole class discussion.

After a short discussion on how children might show or visualize a square number we began to show a model using arrays, like below:

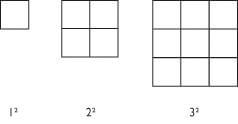
The children working at greater depth were encouraged to consider cubed numbers and show how they might be represented using multi-link cubes without any input from me. This made sure links were made between math concepts, mathematical vocabulary, and learning.

Use ‘sometimes, always, never’ classroom activities

A ‘sometimes, always, never’ activity is another great way to foster reasoning and problem-solving skills. Take the image below:

Here, children are first required to sort the fraction statements into always, sometimes or never being true. The next day, they are moved on to the lesson with the title phrased as a question. So not ‘to identify patterns’, but ‘how does this pattern work?’ with a pattern already presented on the board.

The children, instantly engaged, begin conjecturing, making predictions and thinking about the next patterns in the sequence (this lesson was actually inspired by an Nrich activity- a math education project run by the University of Cambridge) .

5 tips for developing mathematical reasoning in the elementary school

While small changes will not provide the framework you need to properly embed reasoning in the classroom when implemented alongside ideas such as those mentioned above. These tips can help instill greater depth in math in your class for all ability levels.

1. Start lessons with a question.

2. Start lessons with a provocative mathematical statement or mind bender and challenge your class to provide the mathematical proof. Examples include: 

• “N will always = N” 
•  “Multiples of 9 always have the digital sum of 9”.
• “When multiplying decimals the number of decimals places in the answer will be the total number of decimal places in the two numbers being multiplied. (For example, the answer to 2.5 x 3.21, will have 3 decimal places.)”
• “A square is always a rectangle, but a rectangle is not always a square.”

3. Present answers to exam questions as a puzzle to generate discussion and make connections. They can use their repertoire of math skills to explore the relationships between the numbers – does the line signify addition, subtraction, multiplication, etc. Puzzles could even be presented on a simple number line. When framed like this, children like to ‘come up’ with what the question could be:

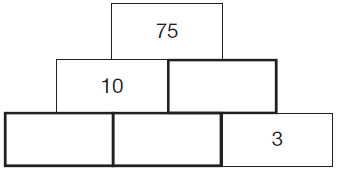
4. Grouping children in threes is the magic number when working through problems. Child one talks through the problem. Child two writes down everybody’s reasoning. Child three actively listens and watches.

5. Include reasoning prompting posters around the classroom. The image below, for example, can be useful to children who are starting to formulate thoughts, predictions and assertions.

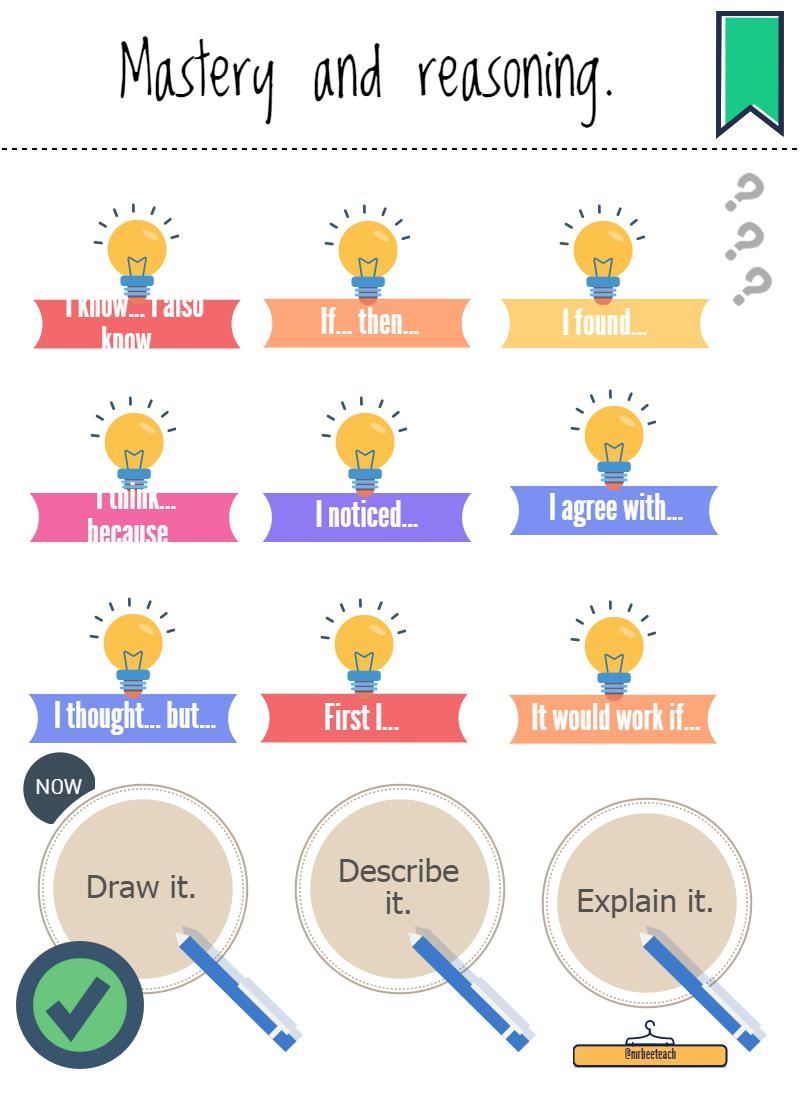
Your students will need an in-depth understanding of facts and concepts to truly succeed. Plus, they will need to be able to use and apply that knowledge to a range of contexts and in classroom discussion, in workbooks and in homework. As such, it’s clear that we need to provide them with a strong foundation of reasoning skills to give them their very best shot at the assessments they must face.

• Math Mastery Toolkit : A Practical Guide To Mastery Teaching And Learning
• Get to Grips With Math Problem Solving KS2
• 21 Math Challenges To Really Stretch Your More Able Students 
• Math Reasoning and Problem Solving CPD Powerpoint
• 20 Math Strategies That Guarantee Progress
• Why You Should Be Incorporating Stem Sentences Into Your Elementary Math Teaching

Ultimate Guide to Metacognition [FREE]

Looking for a summary on metacognition in relation to math teaching and learning?

Check out this guide featuring practical examples, tips and strategies to successfully embed metacognition across your school to accelerate math growth.

Privacy Overview

404 Not found

IEP Goals For Math

Welcome to our blog post on IEP goals for math! Setting goals for your child’s education is an essential step in their academic journey if you’re a teacher or the parent of a student with an Individualized Education Plan (IEP).

Many students find math difficult, so helping your child thrive in school by setting specific, measurable, achievable, relevant, and time-bound (SMART) goals might be helpful. This post will explore  what constitutes a strong IEP objective for math  and offer some starter  examples to get you going . Let’s get started, so grab a coffee and settle in.

What are IEP Goals for Math?

IEP goals for math are  specific, targeted objectives developed for students with an I ndividualized Education Plan (IEP) .  These objectives are intended to assist students with disabilities in improving their arithmetic skills and succeeding in the classroom. Each student’s IEP for math  should be customized to meet their specific requirements  and based on their existing knowledge and capabilities.

They should be  SMART objectives , which are specific, measurable, achievable, relevant, and time-bound. IEP objectives for math could center on several things, like  enhancing fundamental math abilities, problem-solving skills, or deepening comprehension of more complex arithmetic ideas . Parents and educators can assist students with disabilities in overcoming obstacles and succeeding in arithmetic by  creating clear and attainable goals .

For example, a measurable goal for a student may be “To develop basic math skills, such as addition and subtraction, by the end of the school year.” This goal is  measurable  because it has a time limit (by the end of the school year) and a particular objective (improvement). It is  relevant  because it directly relates to the student’s needs and academic pursuits. According to Understood.org , it is feasible since it is reasonable for the student to progress in this area within the allotted time frame. It is also time-bound because it specifies a deadline for completing the task.

It is  feasible  since it is reasonable for the student to progress in this area within the allotted time frame. It is also  time-bound  because it specifies a deadline for completing the task.

Teachers and parents can support students with disabilities to make progress and succeed in the classroom by establishing specific and attainable math IEP goals, as recommended by Great Schools .

It’s critical to frequently evaluate the student’s progress toward their IEP goals and revise them as necessary to keep them demanding yet doable. Read about the Special Education Math Curriculum to learn more.

IEP Goals for Math Problem Solving

IEP goals for math problem-solving are created to assist children with disabilities in acquiring the knowledge and methods required to comprehend and address mathematical problems. These objectives must be precise, catered to each student’s requirements and skills , and based on the student’s present performance levels and long-term goals.

Here are a few  additional points to consider when developing IEP goals for math  problem-solving:

• Focus on the student’s specific needs:  A thorough evaluation of the student’s present math ability should serve as the foundation for developing IEP goals particular to the student’s unique needs and abilities. For example, students who have trouble comprehending word problems can set a goal to enhance their capacity to read and understand mathematical word problems.
• Make the goals measurable:  IEP goals should specify specific performance indicators so that the student’s development may be monitored and assessed. To “increase the student’s accuracy in solving math problems from 75% to 90% within a six-month timeframe,” as an example.
• Make the goals achievable:  Given the student’s abilities and resources, the IEP goals should be achievable and realistic. For the learner to succeed and develop confidence, creating both demanding and challenging but not impossible goals is crucial.
• Make the goals relevant:  The student’s long-term goals and aspirations should be connected to the IEP goals to be meaningful, pertinent to the student’s needs and interests, and significant.
• Set a timeline:  A completion schedule for IEP goals should be included so that the student and their support team know the anticipated timetable for progress.

Functional Math IEP Goals Examples

Functional math IEP goals  focus on helping a student with a disability develop the math skills they need to function independently in their daily life .

Some examples of operational math IEP goals might include:

• “Within a three-month period, the student will be able to identify and make correct change when given a purchase amount and payment up to $5.00.”
• Within six months, the learner will be able to precisely measure and pour ingredients to follow a recipe with 90% accuracy.
• The student can arrange and keep track of appointments and activities within nine months with 80% accuracy using a calendar and telling time.
• Within nine months, “the learner will be able to compare prices and calculate sales tax and savings when shopping, with 80% accuracy.”
• “The student will be able to calculate and track a budget for a 12-month period, covering income and expenses.”

It is important to note that functional math goals  should be specific, measurable, achievable, relevant, and time-bound (SMART) and tailored to the individual student’s needs and abilities .

Jennifer Hanson is a dedicated and seasoned writer specializing in the field of special education. With a passion for advocating for the rights and needs of children with diverse learning abilities, Jennifer uses her pen to educate, inspire, and empower both educators and parents alike.

Related Posts

A comprehensive guide to behavior intervention plans (bip) in special education, esy special education.

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons
• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

Module 1: Problem Solving Strategies

• Last updated
• Save as PDF
• Page ID 10352

Unlike exercises, there is never a simple recipe for solving a problem. You can get better and better at solving problems, both by building up your background knowledge and by simply practicing. As you solve more problems (and learn how other people solved them), you learn strategies and techniques that can be useful. But no single strategy works every time.

Pólya’s How to Solve It

George Pólya was a great champion in the field of teaching effective problem solving skills. He was born in Hungary in 1887, received his Ph.D. at the University of Budapest, and was a professor at Stanford University (among other universities). He wrote many mathematical papers along with three books, most famously, “How to Solve it.” Pólya died at the age 98 in 1985.1

1. Image of Pólya by Thane Plambeck from Palo Alto, California (Flickr) [CC BY

In 1945, Pólya published the short book How to Solve It , which gave a four-step method for solving mathematical problems:

First, you have to understand the problem.

After understanding, then make a plan.

Carry out the plan.

Look back on your work. How could it be better?

This is all well and good, but how do you actually do these steps?!?! Steps 1. and 2. are particularly mysterious! How do you “make a plan?” That is where you need some tools in your toolbox, and some experience to draw upon.

Much has been written since 1945 to explain these steps in more detail, but the truth is that they are more art than science. This is where math becomes a creative endeavor (and where it becomes so much fun). We will articulate some useful problem solving strategies, but no such list will ever be complete. This is really just a start to help you on your way. The best way to become a skilled problem solver is to learn the background material well, and then to solve a lot of problems!

Problem Solving Strategy 1 (Guess and Test)

Make a guess and test to see if it satisfies the demands of the problem. If it doesn't, alter the guess appropriately and check again. Keep doing this until you find a solution.

Mr. Jones has a total of 25 chickens and cows on his farm. How many of each does he have if all together there are 76 feet?

Step 1: Understanding the problem

We are given in the problem that there are 25 chickens and cows.

All together there are 76 feet.

Chickens have 2 feet and cows have 4 feet.

We are trying to determine how many cows and how many chickens Mr. Jones has on his farm.

Step 2: Devise a plan

Going to use Guess and test along with making a tab

Many times the strategy below is used with guess and test.

Make a table and look for a pattern:

Procedure: Make a table reflecting the data in the problem. If done in an orderly way, such a table will often reveal patterns and relationships that suggest how the problem can be solved.

Step 3: Carry out the plan:

Notice we are going in the wrong direction! The total number of feet is decreasing!

Better! The total number of feet are increasing!

Step 4: Looking back:

Check: 12 + 13 = 25 heads

24 + 52 = 76 feet.

We have found the solution to this problem. I could use this strategy when there are a limited number of possible answers and when two items are the same but they have one characteristic that is different.

Videos to watch:

1. Click on this link to see an example of “Guess and Test”

http://www.mathstories.com/strategies.htm

2. Click on this link to see another example of Guess and Test.

http://www.mathinaction.org/problem-solving-strategies.html

Check in question 1:

Place the digits 8, 10, 11, 12, and 13 in the circles to make the sums across and vertically equal 31. (5 points)

Check in question 2:

Old McDonald has 250 chickens and goats in the barnyard. Altogether there are 760 feet . How many of each animal does he have? Make sure you use Polya’s 4 problem solving steps. (12 points)

Problem Solving Strategy 2 (Draw a Picture). Some problems are obviously about a geometric situation, and it is clear you want to draw a picture and mark down all of the given information before you try to solve it. But even for a problem that is not geometric thinking visually can help!

Videos to watch demonstrating how to use "Draw a Picture".

1. Click on this link to see an example of “Draw a Picture”

2. Click on this link to see another example of Draw a Picture.

Problem Solving Strategy 3 ( Using a variable to find the sum of a sequence.)

Gauss's strategy for sequences.

last term = fixed number ( n -1) + first term

The fix number is the the amount each term is increasing or decreasing by. "n" is the number of terms you have. You can use this formula to find the last term in the sequence or the number of terms you have in a sequence.

Ex: 2, 5, 8, ... Find the 200th term.

Last term = 3(200-1) +2

Last term is 599.

To find the sum of a sequence: sum = [(first term + last term) (number of terms)]/ 2

Sum = (2 + 599) (200) then divide by 2

Sum = 60,100

Check in question 3: (10 points)

Find the 320 th term of 7, 10, 13, 16 …

Then find the sum of the first 320 terms.

Problem Solving Strategy 4 (Working Backwards)

This is considered a strategy in many schools. If you are given an answer, and the steps that were taken to arrive at that answer, you should be able to determine the starting point.

Videos to watch demonstrating of “Working Backwards”

https://www.youtube.com/watch?v=5FFWTsMEeJw

Karen is thinking of a number. If you double it, and subtract 7, you obtain 11. What is Karen’s number?

1. We start with 11 and work backwards.

2. The opposite of subtraction is addition. We will add 7 to 11. We are now at 18.

3. The opposite of doubling something is dividing by 2. 18/2 = 9

4. This should be our answer. Looking back:

9 x 2 = 18 -7 = 11

5. We have the right answer.

Check in question 4:

Christina is thinking of a number.

If you multiply her number by 93, add 6, and divide by 3, you obtain 436. What is her number? Solve this problem by working backwards. (5 points)

Problem Solving Strategy 5 (Looking for a Pattern)

Definition: A sequence is a pattern involving an ordered arrangement of numbers.

We first need to find a pattern.

Ask yourself as you search for a pattern – are the numbers growing steadily larger? Steadily smaller? How is each number related?

Example 1: 1, 4, 7, 10, 13…

Find the next 2 numbers. The pattern is each number is increasing by 3. The next two numbers would be 16 and 19.

Example 2: 1, 4, 9, 16 … find the next 2 numbers. It looks like each successive number is increase by the next odd number. 1 + 3 = 4.

So the next number would be

25 + 11 = 36

Example 3: 10, 7, 4, 1, -2… find the next 2 numbers.

In this sequence, the numbers are decreasing by 3. So the next 2 numbers would be -2 -3 = -5

-5 – 3 = -8

Example 4: 1, 2, 4, 8 … find the next two numbers.

This example is a little bit harder. The numbers are increasing but not by a constant. Maybe a factor?

So each number is being multiplied by 2.

16 x 2 = 32

1. Click on this link to see an example of “Looking for a Pattern”

2. Click on this link to see another example of Looking for a Pattern.

Problem Solving Strategy 6 (Make a List)

Example 1 : Can perfect squares end in a 2 or a 3?

List all the squares of the numbers 1 to 20.

1 4 9 16 25 36 49 64 81 100 121 144 169 196 225 256 289 324 361 400.

Now look at the number in the ones digits. Notice they are 0, 1, 4, 5, 6, or 9. Notice none of the perfect squares end in 2, 3, 7, or 8. This list suggests that perfect squares cannot end in a 2, 3, 7 or 8.

How many different amounts of money can you have in your pocket if you have only three coins including only dimes and quarters?

Quarter’s dimes

0 3 30 cents

1 2 45 cents

2 1 60 cents

3 0 75 cents

Videos demonstrating "Make a List"

Check in question 5:

How many ways can you make change for 23 cents using only pennies, nickels, and dimes? (10 points)

Problem Solving Strategy 7 (Solve a Simpler Problem)

Geometric Sequences:

How would we find the nth term?

Solve a simpler problem:

1, 3, 9, 27.

1. To get from 1 to 3 what did we do?

2. To get from 3 to 9 what did we do?

Let’s set up a table:

Term Number what did we do

Looking back: How would you find the nth term?

Find the 10 th term of the above sequence.

Let L = the tenth term

Problem Solving Strategy 8 (Process of Elimination)

This strategy can be used when there is only one possible solution.

I’m thinking of a number.

The number is odd.

It is more than 1 but less than 100.

It is greater than 20.

It is less than 5 times 7.

The sum of the digits is 7.

It is evenly divisible by 5.

a. We know it is an odd number between 1 and 100.

b. It is greater than 20 but less than 35

21, 23, 25, 27, 29, 31, 33, 35. These are the possibilities.

c. The sum of the digits is 7

21 (2+1=3) No 23 (2+3 = 5) No 25 (2 + 5= 7) Yes Using the same process we see there are no other numbers that meet this criteria. Also we notice 25 is divisible by 5. By using the strategy elimination, we have found our answer.

Check in question 6: (8 points)

Jose is thinking of a number.

The number is not odd.

The sum of the digits is divisible by 2.

The number is a multiple of 11.

It is greater than 5 times 4.

It is a multiple of 6

It is less than 7 times 8 +23

What is the number?

Click on this link for a quick review of the problem solving strategies.

https://garyhall.org.uk/maths-problem-solving-strategies.html

Join Pilot Waitlist

Home » SEL Implementation » Achieving Math Success: Understanding IEP Goals and Strategies

Achieving Math Success: Understanding IEP Goals and Strategies

Key takeaways.

• Mathematics is essential for academic and everyday life, but students with math difficulties can find success challenging.
• Individualized Education Programs (IEPs) play a crucial role in supporting students with math difficulties through tailored goals and strategies.
• IEP goals should be specific, measurable, attainable, relevant, and time-bound (SMART) and aligned with the math curriculum.
• Common IEP goals for math include developing numeracy skills, enhancing problem-solving skills, and improving math fluency.
• Strategies for achieving math success through IEP goals involve individualized instruction, multi-sensory approaches, explicit instruction, and regular progress monitoring.
• Collaboration between educators, parents, and students is vital for effective implementation of IEP goals and strategies.

Introduction: Achieving Math Success: Understanding IEP Goals and Strategies

Mathematics is a fundamental skill that plays a crucial role in both academic and everyday life. From calculating expenses to solving complex problems, math is a skill that we rely on throughout our lives. However, for students with math difficulties, achieving math success can be a challenging journey. This is where Individualized Education Programs (IEPs) come into play. In this blog post, we will explore the importance of IEP goals and strategies in supporting students with math difficulties.

What are IEP goals?

IEP goals are specific objectives that are designed to address the unique needs of students with disabilities. These goals are created collaboratively by a team of educators, parents, and other professionals, and they serve as a roadmap for the student’s educational journey. In the context of math, IEP goals are tailored to address the specific math difficulties that a student may be facing.

It is important to align IEP goals with the math curriculum to ensure that students are receiving the necessary support to succeed in their math education. By aligning IEP goals with the curriculum, educators can ensure that students are working towards the same standards as their peers, while also receiving the additional support they need.

Well-defined IEP goals for math should be specific, measurable, attainable, relevant, and time-bound (SMART). This means that the goals should clearly state what the student is expected to achieve, how progress will be measured, and when the goal is expected to be achieved. By setting SMART goals, educators can track the student’s progress and make necessary adjustments to their instruction and support.

Common IEP goals for math

IEP goals for math can vary depending on the individual needs of the student. However, there are some common areas that are often targeted in IEP goals for math:

Numeracy skills

Developing strong numeracy skills is essential for math success. IEP goals in this area may focus on:

• Counting and number recognition
• Addition and subtraction
• Multiplication and division

Problem-solving skills

Problem-solving is a critical skill in math. IEP goals in this area may include:

• Understanding and solving word problems
• Applying mathematical concepts to real-life situations

Math fluency

Math fluency refers to the ability to quickly and accurately perform basic math operations. IEP goals in this area may focus on:

• Speed and accuracy in basic math operations
• Mental math strategies

Strategies for achieving math success through IEP goals

Now that we understand the importance of IEP goals in supporting math success, let’s explore some strategies that can help students achieve these goals:

Individualized instruction and accommodations

Modifying instructional materials, providing visual aids and manipulatives, and using assistive technology can help students with math difficulties access the curriculum and understand mathematical concepts.

Multi-sensory approaches

Incorporating hands-on activities, utilizing auditory and visual cues, and engaging in kinesthetic learning can enhance students’ understanding and retention of math concepts.

Explicit instruction and guided practice

Breaking down complex concepts into smaller steps, providing clear explanations and demonstrations, and offering guided practice opportunities can support students in mastering math skills.

Regular progress monitoring and feedback

Assessing students’ understanding and progress, providing constructive feedback and reinforcement, and adjusting strategies and goals as needed can ensure that students are making continuous progress towards their math goals.

Collaboration between educators, parents, and students

Collaboration between educators, parents, and students is essential in supporting math success. Open communication and teamwork can help ensure that everyone is working towards the same goals and that the student’s needs are being met.

Involving parents in goal-setting and progress monitoring can provide valuable insights and support at home. Encouraging student self-advocacy and active participation in their own education can empower them to take ownership of their learning and seek help when needed.

Achieving math success is possible for students with math difficulties through the support of well-defined IEP goals and effective strategies. By aligning IEP goals with the math curriculum, utilizing individualized instruction and accommodations, and fostering collaboration between educators, parents, and students, we can create a supportive environment where students can thrive in math.

Looking for More Information on How to Achieve Math Success? Discover Resources on Understanding IEP Goals and Strategies Here

If you are looking for resources to support your child’s math journey, consider starting your Everyday Speech free trial. Everyday Speech offers a wide range of social-emotional learning resources, including videos, worksheets, and activities, that can help students develop the skills they need to succeed in math and beyond.

Start your Everyday Speech Free trial

Remember, with the right support and strategies, every student can achieve math success!

Related Blog Posts:

Pragmatic language: enhancing social skills for meaningful interactions.

Pragmatic Language: Enhancing Social Skills for Meaningful Interactions Pragmatic Language: Enhancing Social Skills for Meaningful Interactions Introduction: Social skills play a crucial role in our daily interactions. They enable us to navigate social situations,...

Preparing for Success: Enhancing Social Communication in Grade 12

Preparing for Success: Enhancing Social Communication in Grade 12 Key Takeaways Strong social communication skills are crucial for academic success and building meaningful relationships in Grade 12. Social communication includes verbal and non-verbal communication,...

Preparing for Success: Enhancing Social Communication in Grade 12 Preparing for Success: Enhancing Social Communication in Grade 12 As students enter Grade 12, they are on the cusp of adulthood and preparing for the next chapter of their lives. While academic success...

FREE MATERIALS

Better doesn’t have to be harder, social skills lessons students actually enjoy.

Be the best educator you can be with no extra prep time needed. Sign up to get access to free samples from the best Social Skills and Social-Emotional educational platform.

Get Started Instantly for Free

Complete guided therapy.

The subscription associated with this email has been cancelled and is no longer active. To reactivate your subscription, please log in.

If you would like to make changes to your account, please log in using the button below and navigate to the settings page. If you’ve forgotten your password, you can reset it using the button below.

Unfortunately it looks like we’re not able to create your subscription at this time. Please contact support to have the issue resolved. We apologize for the inconvenience. Error: Web signup - customer email already exists

Welcome back! The subscription associated with this email was previously cancelled, but don’t fret! We make it easy to reactivate your subscription and pick up right where you left off. Note that subscription reactivations aren't eligible for free trials, but your purchase is protected by a 30 day money back guarantee. Let us know anytime within 30 days if you aren’t satisfied and we'll send you a full refund, no questions asked. Please press ‘Continue’ to enter your payment details and reactivate your subscription

Notice About Our SEL Curriculum

Our SEL Curriculum is currently in a soft product launch stage and is only available by Site License. A Site License is currently defined as a school-building minimum or a minimum cost of $3,000 for the first year of use. Individual SEL Curriculum licenses are not currently available based on the current version of this product.

By clicking continue below, you understand that access to our SEL curriculum is currently limited to the terms above.

Problem Solving Skills and Objectives

Regardless of what they do for a living or where they live, most people spend most of their waking hours, at work or at home, solving problems. Most problems we face are small, some are large and complex, but they all need to be solved in a satisfactory way. (Robert Harris, 1998)

Having the support of others in solving problems is important. Diversity of thought and of problem solving style can result in better solutions.

The objectives for this module are:

• Identify different problem solving styles
• Identify methods appropriate for solving problems
• Apply methods to specific problems
• Apply problem solving skills when working with children.

Licensed under the Creative Commons Attribution-NonCommercial-ShareAlike 2.5 License

Brought to you by CReducation.org .

404 Not found

Goals and Objectives

Math and Computer Science

Mathematics Goals and Objectives

Goal #1: Problem-Solving.   (ULG 1,5,6)

• Be able to use problem-solving techniques to formulate a mathematical model for and solve a complex problem.
• Be able to make appropriate use of technology in the solution of a mathematical problem.

Goal #2: Abstraction and Proof.   (ULG 1,5)

• Be able to read and comprehend a mathematical argument, identifying any flaws in its reasoning.
• Be able to use mathematical reasoning to prove or disprove conjectures.
• Be able to write formal mathematical proofs.
• Be able to use abstraction and generalization to make and test conjectures and to revise them as necessary.

Goal #3: Communication.   (ULG 1,5)

• Be able to communicate sound mathematical reasoning and solutions of mathematical problems in writing.
• Be able to communicate sound mathematical reasoning and solutions of mathematical problems through oral presentations.
• Be able to collaborate with peers to solve mathematical problems.
• Use a variety of representations of mathematical ideas to support and deepen students' mathematical understanding.   (Secondary Education majors)

Goal #4: Breadth.   (ULG 1,5,6)

• Possess the mathematical content knowledge and skills from several foundational areas of mathematics, including calculus, algebra, discrete mathematics, and linear algebra.
• Identify an array of other areas of mathematics and how they interrelate.
• Possess a deep understanding of the mathematical content knowledge and skills taught at the secondary level.   (Secondary Education majors)

Goal #5: Depth.   (ULG 1,5)

• Complete a capstone project and/or an extended study of an advanced area of undergraduate mathematics.
• Possess a pedagogical knowledge specific to mathematics teaching and learning.   (Secondary Education majors)

Goal #6: Independent Learning.   (ULG 1,5,6)

• Be able to read and learn from mathematical literature such as textbooks and journals.
• Be adequately prepared for success in graduate school, secondary teaching, and careers requiring analytical skills.

Computer Science Goals and Objectives

• Be able to apply appropriate programming techniques to solve small-scale problems (i.e., in the small). This means choosing appropriate language constructs (e.g., conditions, repetition, function and class decomposition), data structures (e.g., arrays, stacks, associative arrays, heaps), and algorithms to solve a fairly small problem.
• Be able to select appropriate components to solve large-scale problems (i.e., in the large). This means choosing between appropriate data structures, algorithms, and system-level components (e.g., servers, databases, network protocols).

Goal #2: Independent Learning.   (ULG 1,5,6)

• Be able to complete a project which uses technologies not covered in any class. This may include completely new technology or the use of unexplored features during coursework.
• Be able to solve problems in multiple languages (e.g., Current Languages, Programming Languages, Internet Development).

Goal #3: Ethical and Professional Behavior.   (ULG 3)

• Be guided by ethical principles in their careers as informed by Christian values.

Goal #4: Communication.   (ULG 1,5)

• Be able to to communicate in writing (e.g., technical reports, project documentation, software development artifacts).
• Be able to communicate orally (e.g., new technology not covered in class, project presentations, code reviews)..
• Be able to document program code using appropriate tools (e.g., JavaDoc. UML).

REQUEST INFO

PLAN YOUR VISIT

SCHOLARSHIPS

PRIVACY STATEMENT

Ouachita Baptist University's website uses cookies to improve user experience, analyze site usage and aid in student recruitment. To learn more, read Ouachita's privacy policy .

I understand

Math Interventions

Introduction.

• Subitizing Interventions
• Counting Interventions: Whole Numbers Less Than 30
• Counting Interventions: Whole Numbers Greater Than 30 (Place Value)
• Counting Interventions: Fractions
• Counting Interventions: Decimals
• Composing and Decomposing Numbers Interventions
• Rounding Interventions
• Number Sense Lesson Plans
• Addition and Subtraction Facts
• Multiplication and Division Facts
• Computational Fluency Lesson Plans
• Understanding the Problem Interventions
• Planning and Executing a Solution Interventions
• Monitoring Progress & Reflecting on a Solution Interventions
• Problem-Solving Process Interventions
• Problem-Solving Lesson Plans
• Identifying Essential Variables Interventions
• Direct Models Interventions
• Counting On/Back Interventions
• Deriving Interventions
• Interpreting the Results Interventions
• Mathematical Modeling Lesson Plans
• Math Rules and Concepts Interventions
• Math Rules and Concepts Lesson Plans

You can use either  Explicit Instruction  or Self-Regulated Strategy Development when you intervene to support your student's problem solving skills. The following lesson plan targets a specific problem-solving skill using explicit instruction. As you read this plan, consider: 

How does this plan support objective mastery?

Problem Solving Intervention Plan

Art, E. (2017). Problem solving intervention packet. New York, NY: Relay Graduate School of Education.

This lesson plan supports objective mastery because the teacher employs Principles of Specialized instruction to help the student visualize Part/Part/Whole (Part Unknown) problems to identify what she is supposed to figure out. In this lesson plan, she isolates the skill (identifying what the problem is), and uses explicit instruction to teach the student how to identify two what is happening in the story and what she is trying to figure out. After she explains the process she'll take, she uses metacognition and shows the student how she asks these two questions as she is reading. Finally, she builds in multiple at-bats so that the student has the opportunity to practice this strategy over and over so that she can reach her objective.

• << Previous: Problem-Solving Process Interventions
• Next: Identifying Essential Variables Interventions >>
• Last Updated: Feb 14, 2024 6:46 PM
• URL: https://relay.libguides.com/math-interventions

• Skip to main content
• Skip to main navigation

Mathematics

• Contact & Visitor Info
• Staff (Admin & Advising)
• Faculty (Professors)
• Visiting Scholars
• Graduate students
• (MATH in campus directory)
• Apply to Graduate School
• Newly Admitted Grads
• Ph.D. Program
• M.A. Program
• 4+1 Pathway
• Directed Reading Program
• Teaching Assistantships
• Graduate Handbook
• Graduate Division Policies
• Title IX Policies
• Issue Resolution Resources
• Health and Well-Being Resources
• Graduate Program Forms
• Request Funding (current grads)
• Advising Office Info
• Calculus Series Transitions Policy
• CSET Waivers For SMP
• Degree Requirements
• Enrollment Basics and Help
• Permission To Enroll Form
• Student Forms and Resources
• Declaring the Major/Minor
• Undergraduate Awards
• Algebra & Number Theory
• Analysis & Geometry
• 23-24 offerings
• Availability
• Curriculum notes
• Descriptions
• List from catalog
• Math Placement
• UCSC Navigator
• Online courses
• Summer Session
• TA office hours
• Mathematics Colloquium
• Geometry & Analysis
• Graduate Colloquium
• Undergraduate Colloquium
• Other Seminars
• Math Events Calendar
• External Colloquia
• Mathematics General Fund
• Fellowships: Mathematics
• Divisional Development Office

Home / Undergraduate / Student Forms and Resources / Undergraduate Program Learning Outcomes

Mathematics Undergraduate Student Learning Objectives



The Mathematics Department at U.C. Santa Cruz offers three tracks leading to the Mathematics B.A. degree as well as a Minor in Mathematics.

The Mathematics program promotes mathematical skills and knowledge for their intrinsic beauty, effectiveness in developing proficiency in analytical reasoning, and utility in modeling and solving real world problems. To responsibly live within and participate in the transformation of a rapidly changing, complex, and interdependent society, students must develop and unceasingly exercise their analytical abilities. Students who have learned to logically question assertions, recognize patterns, and distinguish the essential and irrelevant aspects of problems can think deeply and precisely, nurture the products of their imagination to fruition in reality, and share their ideas and insights while seeking and benefiting from the knowledge and insights of others.

Students majoring in Mathematics attain proficiency in

Critical thinking

     The ability to identify, reflect upon, evaluate, integrate, and apply different types of in- formation and knowledge to form independent judgments. Analytical and logical thinking and the habit of drawing conclusions based on quantitative information.

Problem solving

     The ability to assess and interpret complex situations, choose among several potentially appropriate mathematical methods of solution, persist in the face of difficulty, and present full and cogent solutions that include appropriate justification for their reasoning.

Effective communication

     The ability to communicate and interact effectively with different audiences, developing their ability to collaborate intellectually and creatively in diverse contexts, and to appre- ciate ambiguity and nuance, while emphasizing the importance of clarity and precision in communication and reasoning.

     Students acquire and enhance these abilities in mathematical contexts, but the acquired habits of rigorous thought and creative problem-solving are invaluable in all aspects of life. These skills are acquired through experience in the context of studying specific mathematical topics and exploring problems chosen to challenge students’ abilities, spurring them on to acquire new techniques and abandon familiar but restrictive habits of thought. The overarching objectives can be realized in terms of more focused, appraisable objectives specific to mathematics as follows:

     Students will

          • understand the basic rules of logic, including the role of axioms or assumptions

          • appreciate the role of mathematical proof in formal deductive reasoning

          • be able to distinguish a coherent argument from a fallacious one, both in mathematical reasoning and in everyday life

          • understand and be able to articulate the differences between inductive and deductive reasoning

          • proficiently construct logical arguments and rigorous proofs

          • formulate conjectures by abstracting general principles from examples.

     Courses: 20AB, 100, 101, 105AB, 110, 111AB, 117, 118, 160, 161.

     Students will be able to

• formulate and solve abstract mathematical problems
• recognize real-world problems that are amenable to mathematical analysis, and formulate mathematical models of such problems
• apply mathematical methodologies to open-ended real-world problems
• recognize connections between different branches of mathematics
• recognize and appreciate the connections between theory and applications.

    Courses: 19AB, 20AB, 22, 23AB, 24, 100, 101, 103AB, 106, 107, 114, 115, 116, 134, 145.

• present mathematics clearly and precisely to an audience of peers and faculty
• appreciate the role of mathematical proof as a means of conveying mathematical knowledge
• understand the differences between proofs and other less formal arguments
• make vague ideas precise by formulating them in mathematical language
• describe mathematical ideas from multiple perspectives
• explain fundamental mathematical concepts or analyses of real-world problems to non-mathematicians.

   Courses: 100, 101, 105AB, 111AB, 188, 189, 194, 195.

Subject-specific knowledge

     Students must demonstrate mastery in the three basic areas of mathematics: algebra, analysis, and topology/geometry on a basic level in lower division courses and at an advanced level in upper division courses.

Algebra, number theory, and combinatorics

     "we must endeavor to persuade those who are prescribe to be the principal men of our State to go and learn arithmetic, not as amateurs, but they must carry on the study until they see the nature of numbers with the mind only; not like merchants or retail-traders, with a view to buying or selling, but for the sake of their military applications and the benefit of the soul. . . I must add how charming the science is, and in how many ways it conduces to our desired end, if pursued in the spirit of a philosopher, and not of a shopkeeper!"

-Plato, The Republic

     Abstract algebra involves the study of algebraic structures such as groups, rings, fields, modules, vector spaces, and algebras. Linear algebra is a crucial subfield of algebra, both as an introduction to abstract algebraic structures and as a body of advanced results of immense importance in diverse areas of application. Number theorists study properties of the integers, as well as those of mathematical objects constructed from or generalizing the integers. Combinatorics involves finite or countable discrete structures, such as abstract graphs.

    Courses: Math 21, 100, 110, 111AB, 114, 115, 116, 117, 118, 120, 134.

Calculus and analysis

            Although the nature of,  … is in no way altered when they appear. . . on the right-hand side of the differential equation, nonetheless their role and the character of the equation are thereby altered. . . They are brought into the world unilaterally, shadow figures lacking the body which cast them ...The initiative is thus shifted from the right-hand pole, the algebraic, to the left-hand one, the symbolic.

Karl Marx, On the Differential

     Analysis extends and refines calculus; it encompasses differentiation, integration, measure, limits, infinite series, and analytic functions, primarily in the context of real and complex number systems. In much of analysis, the emphasis is not on finding explicit solutions to specific problems, but rather on determining which problems can be solved and what general properties solutions may share. Ordinary and partial differential equations play a central role in analysis, and are widely used in modeling real-world systems.

   Courses: Math 19AB, 20AB, 23AB, 24, 100, 103AB, 105AB, 106, 107, 140, 145, 148.

Geometry and topology

     "My noble friend, geometry will draw the soul towards truth, and create the spirit of philosophy . . . nothing should be more sternly laid down than that the inhabitants of your fair city should by all means learn geometry. Moreover, the science has significant indirect effects...in all departments of knowledge, as experience proves, any one who has studied geometry enjoys infinitely quicker understanding than one who has not."

     Geometry explores the implementation and far-reaching consequences of systems of mea- surement; topology addresses questions pertaining to shape and global structure. Non- Euclidean geometry, differential geometry (the extension of calculus to mapping of curves, surfaces, and their generalizations), and algebraic geometry generalize key results and tech- niques from Euclidean geometry to both familiar and exotic settings. In algebraic and differ- ential topology, techniques from diverse areas of mathematics are used to infer information about the shapes and related properties of spaces.

   Courses: Math 23AB, 121AB, 124, 128AB, 129, 130.

     This subdivision of mathematics is not sharp: the areas of overlap between the three main areas of mathematics are of great interest and importance. For example, analytic number theory as the study of the integers by means of tools from real and complex analysis, while differential geometry focuses on the interplay between analysis and geometry. The importance of all three areas, the influence of each on the others, and the insight to be gained by considering one area from perspectives commonly associated to another one are all emphasized in the Mathematics curriculum—as can be seen in the course matrix, many courses involve material from multiple areas.

The Mathematics Department offers three tracks within the Mathematics major:

Pure Mathematics

     Students in the Pure Mathematics track often go on to graduate study in mathematics; the pathway emphasizes the importance of a well-rounded, in-depth mathematical education, and includes advanced coursework in algebra, analysis, and geometry.

Computational Mathematics

     Students in the Computational Mathematics track explore applications of mathematics in other fields and gain experience in mathematical modeling of real-world phenomena using ordinary and partial differential equations, approximation and optimization techniques, linear programming, or game theory.

Mathematics Education

     Students in the Mathematics Education track prepare for a career in K–12 mathematics education; students acquire in-depth knowledge of subjects covered at an introductory level in the classroom, including number theory, classical geometry, and the history of mathematics, and gain experience in teaching mathematics in an accessible and intuitive, but precise, manner.

Curriculum matrix

     All of the key objectives are addressed to some extent in all courses. For example, the ability to formulate precise mathematical statements and to reason logically are essential skills that are progressively developed throughout the curriculum. However, some skills are more heavily emphasized and utilized in some courses than in others. Some courses are specifically intended to help students move to a new level of proficiency with a particular portfolio of skills, while others are accessible only to students who have already reached a given level; the latter courses make heavy use of particular skills, and thus enhance and reinforce the student’s mastery of it, but the skills themselves are not the primary focus of such courses. Some connections between the key objectives, main subject-specific areas, and courses are indicated in the following tables of lower and upper division mathematics courses.

• Academic Program Overview
• Contiguous Bachelor’s/Master’s Pathway (4+1 Pathway)
• CSET Subject Matter Waiver Program
• Declaring the Major/Minor and Appeals
• Directed Reading Program (new)
• Enrollment Request and Permission Number Form
• Tutors List
• Major Checklists and Flowcharts
• Careers in Mathematics
• Transferring Math Courses
• Undergraduate Program Learning Outcomes
• Student Resources/Academic Support
• AP Score Verification
• Advising questions ? Please email [email protected]

Mathematics Department 4111 McHenry (North block) ------- Phone: 831.459.2400 Fax: 831.459.3260

Directions to McHenry

UCSC Links:

• Division of Physical & Biological Sciences
• University Library
• Science & Engineering Library
• Our entry in the UCSC Catalog
• Register for the quarter
• Report an accessibility barrier
• Land Acknowledgment
• Accreditation

Last modified: June 29, 2022 128.114.113.87

• Open Middle Problems
• Real World Problems
• Online Workshops

Content and Language Objectives using the Standards for Mathematical Practice

• SWBAT analyze givens, constraints, relationships, and goals. (MP1)
• SWBAT consider analogous problems, and try special cases and simpler forms of the original problem in order to gain insight into its solution. (MP1)
• SWBAT monitor and evaluate their progress and change course if necessary. For example older students may transform algebraic expressions or change the viewing window on their graphing calculator to get the information they need, depending on the context of the problem. (MP1)
• SWBAT check their answers to problems using a different method, and they continually ask themselves, “Does this make sense?” (MP1)
• SWBAT make sense of quantities and their relationships in problem situations. (MP2)
• SWBAT decontextualize a problem by abstracting a given situation, representing it symbolically, and manipulating the representing symbols as if they have a life of their own without necessarily attending to their referents. (MP2)
• SWBAT contextualize a problem by pausing as needed during the manipulation process in order to probe into the referents for the symbols involved. (MP2)
• SWBAT create a coherent representation of the problem at hand (MP2)
• SWBAT consider the units involved (MP2)
• SWBAT attend to the meaning of quantities, not just how to compute them (MP2)
• SWBAT know and flexibly use different properties of operations and objects. (MP2)
• SWBAT analyze situations by breaking them into cases, and can recognize and use counterexamples. (MP3)
• In early grades, this might be as simple as writing an addition equation to describe a situation. (MP4)
• In middle grades, a student might apply proportional reasoning to plan a school event or analyze a problem in the community. (MP4)
• By high school, a student might use geometry to solve a design problem or use a function to describe how one quantity of interest depends on another. (MP4)
• SWBAT make assumptions and approximations to simplify a complicated situation, realizing that these may need revision later. (MP4)
• SWBAT identify important quantities in a practical situation and map their relationships using such tools as diagrams, two-way tables, graphs, flowcharts and formulas. (MP4)
• SWBAT routinely interpret their mathematical results in the context of the situation and reflect on whether the results make sense, possibly improving the model if it has not served its purpose. (MP4)
• SWBAT consider the available tools when solving a mathematical problem. These tools might include pencil and paper, concrete models, a ruler, a protractor, a calculator, a spreadsheet, a computer algebra system, a statistical package, or dynamic geometry software. (MP5)
• SWBAT be sufficiently familiar with tools appropriate for their grade or course to make sound decisions about when each of these tools might be helpful, recognizing both the insight to be gained and their limitations. For example high school students may analyze graphs of functions and solutions generated using a graphing calculator. They detect possible errors by strategically using estimation and other mathematical knowledge. (MP5)
• SWBAT to use technology to enable them to visualize the results of varying assumptions, explore consequences, and compare predictions with data when making mathematical models. (MP5)
• SWBAT identify relevant external mathematical resources, such as digital content located on a website, and use them to pose or solve problems. (MP5)
• SWBAT use technological tools to explore and deepen their understanding of concepts. (MP5)
• SWBAT state the meaning of the symbols they choose, including using the equal sign consistently and appropriately. (MP6)
• SWBAT carefully specify units of measure, labeling axes to clarify the correspondence with quantities in a problem. (MP6)
• SWBAT calculate accurately, efficiently, and express numerical answers with a degree of precision appropriate for the problem context. (MP6)
• Elementary SWBAT notice that three and seven more is the same amount as seven and three more (MP7)
• Elementary SWBAT sort a collection of shapes according to how many sides the shapes have. (MP7)
• Middle school SWBAT see 7 × 8 equals 7 × 5 + 7 × 3, in preparation for learning about the distributive property. (MP7)
• High school SWBAT see in the expression x2 + 9x + 14 that the 14 is also 2 × 7 and the 9 is also 2 + 7.
• High school SWBAT recognize the significance of an existing line in a geometric figure and can use the strategy of drawing an auxiliary line for solving problems. (MP7)
• SWBAT step back for an overview and shift perspective. (MP7)
• SWBAT see complicated things, such as some algebraic expressions, as single objects or as being composed of several objects. For example, they can see 5 – 3(x – y)2 as 5 minus a positive number times a square and use that to realize that its value cannot be more than 5 for any real numbers x and y. (MP7)
• Upper elementary SWBAT might notice when dividing 25 by 11 that they are repeating the same calculations over and over again, and conclude they have a repeating decimal. (MP8)
• Middle school SWBAT abstract the equation (y – 2)/(x – 1) = 3 by paying attention to the calculation of slope as they repeatedly check whether points are on the line through (1, 2) with slope 3(MP8)
• High school SWBAT notice the regularity in the way terms cancel when expanding (x – 1)(x + 1), (x – 1)(x2 + x + 1), and (x – 1)(x3 + x2 + x + 1) leading them to the general formula for the sum of a geometric series. (MP8)
• SWBAT maintain oversight of the process while attending to the details as they work to solve a problem. (MP8)
• SWBAT continually evaluate the reasonableness of their intermediate results. (MP8)
• SWBAT explain to themselves the meaning of a problem and looking for entry points to its solution. (MP1)
• SWBAT make conjectures about the form and meaning of the solution and plan a solution pathway rather than simply jumping into a solution attempt. (MP1)
• SWBAT explain correspondences between equations, verbal descriptions, tables, and graphs or draw diagrams of important features and relationships, graph data, and search for regularity or trends. For example, younger students may use concrete objects or pictures to help conceptualize and solve a problem, as necessary. (MP1)
• SWBAT understand the approaches of others to solving complex problems and identify correspondences between different approaches. (MP1)
• SWBAT understand and use stated assumptions, definitions, and previously established results in constructing arguments. (MP3)
• SWBAT make conjectures and build a logical progression of statements to explore the truth of their conjectures. (MP3)
• SWBAT justify their conclusions, communicate them to others, and respond to the arguments of others. (MP3)
• SWBAT reason inductively about data, making plausible arguments that take into account the context from which the data arose. (MP3)
• Elementary SWBAT construct arguments using concrete referents such as objects, drawings, diagrams, and actions. Such arguments can make sense and be correct, even though they are not generalized or made formal until later grades. (MP3)
• Older SWBAT learn to determine domains to which an argument applies. (MP3)
• SWBAT listen to or read the arguments of others, decide whether they make sense, and ask useful questions to clarify or improve the arguments. (MP3)
• SWBAT analyze relationships (such tools as diagrams, two-way tables, graphs, flowcharts and formulas) between important quantities to draw conclusions. (MP4)
• SWBAT communicate precisely to others. (MP6)
• SWBAT use clear definitions in discussion with others and in their own reasoning. (MP6)
• Elementary SWBAT give carefully formulated explanations to each other. (MP6)
• High school SWBAT examine claims and make explicit use of definitions. (MP6)

This is a great list/post. I wonder about perhaps developing some kind of graphic organizer overlay showing the connections to the 4 language domains READING, WRITING, LISTENING AND SPEAKING? Will put this on my TO DO list and share once it is done.

I am wondering if Norma has made any progress? I’m thinking this would be helpful as our school pivots to thinking about literacy as it applies to each content area.

Maybe this is common understanding, but I’m not familiar with the acronym “SWBAT”

Students Will Be Able To

Thank you! I really appreciate a place to ask questions and all the shared thinking.

• Pingback: Common core math - math | Pearltrees

It is nice to have students be aware of the mathematical practices that they are developing. But I think it is also helpful to the students, and even motivational, for them to be aware of the specific content they are learning in a given lesson. This *can* be done in discovery lessons without giving away the punch line. My favorite example of how to do this can be seen in this video of a grade 4 lesson at the Chicago Lesson Study Conference in May, 2016:

http://www.lsalliance.org/videos/Prieto_gr4_fractions_May_2016.mp4

In this lesson, the teacher, Alexandra Johansen, presents a problem to the students and has them identify why it is a *problem*, i.e. what is new about it. From there, she invites them to articulate a “guiding question” for the day (which you can see at 3:54 in the video). In this lesson, the guiding question is, “How do mathematicians add fractions with different denominators?”

Thanks for sharing this Tom. This is definitely a great alternative as well. I appreciate you adding this to the conversation for teachers to consider.

Leave a Reply Cancel reply

Your email address will not be published. Required fields are marked *

Save my name, email, and website in this browser for the next time I comment.

Sign me up to receive updates including new blog posts, lessons, and events.

Don't subscribe All new comments Replies to my comments Notify me of followup comments via e-mail. You can also subscribe without commenting.

Post comment

• Primary Hub
• Art & Design
• Design & Technology
• Health & Wellbeing
• Secondary Hub
• Citizenship
• Primary CPD
• Secondary CPD
• Book Awards
• All Products
• Primary Products
• Secondary Products
• School Trips
• Trip Directory
• Trips by Subject
• Trips by Type
• Trips by Region
• Submit a Trip Venue

Trending stories

Top results.

• Teaching Resources
• Maths Problem Solving Questions

Maths problem solving questions – KS2 lesson plan

Zipped file containing 3 PDFs

The need to prepare children for their times tables test often means that we overlook building their reasoning and problem-solving skills. This is to allow time to develop number fluency and recall.

However, NRICH’s curriculum-linked activities enable your learners to become more fluent alongside developing their reasoning and problem-solving skills.

In this maths problem solving questions lesson you’ll work through NRICH’s Shape Times Shape worksheet to practise and develop some of these underused skills. 

Maths problem solving questions KS2 learning objectives

• Times tables facts  
• Reasoning skills  
• How to think about finding a way to a solution 
• The idea of a symbol (in this case a shape) representing a number 

Make sure all the children can see the Shape Times Shape worksheet. You could display it on the board or give out copies of the printable sheet.

Try to say very little as you introduce the task. Just review what the problem itself states, then give learners a few minutes to think on their own. 

NRICH is a maths outreach project, which is a collaboration between the Faculties of Education and Mathematics, based at the University of Cambridge. NRICH resources are free for teachers to use with their classes. 

Similar resources

• Place value worksheets – Free maths PDFs for KS1 and KS2
• Bar modelling maths – Worksheets and CPD resources
• Bar model maths – Singapore-style lesson plan
• Probability KS2 – Playful dice investigation lesson plan
• Fractions SATs questions – KS2 maths worksheets

Sign up to our newsletter

You'll also receive regular updates from Teachwire with free lesson plans, great new teaching ideas, offers and more. (You can unsubscribe at any time.)

Which sectors are you interested in?

Early Years

Thank you for signing up to our emails!

Explore teaching packs

Why join Teachwire?

Get what you need to become a better teacher with unlimited access to exclusive free classroom resources and expert CPD downloads.

Exclusive classroom resource downloads

Free worksheets and lesson plans

CPD downloads, written by experts

Resource packs to supercharge your planning

Special web-only magazine editions

Educational podcasts & resources

Access to free literacy webinars

Newsletters and offers

Create free account

By signing up you agree to our terms and conditions and privacy policy .

Already have an account? Log in here

Thanks, you're almost there

To help us show you teaching resources, downloads and more you’ll love, complete your profile below.

Welcome to Teachwire!

Set up your account.

Lorem ipsum dolor sit amet consectetur adipisicing elit. Commodi nulla quos inventore beatae tenetur.

I would like to receive regular updates from Teachwire with free lesson plans, great new teaching ideas, offers and more. (You can unsubscribe at any time.)

Log in to Teachwire

Not registered with Teachwire? Sign up for free

Reset Password

Remembered your password? Login here

The home of mathematics education in New Zealand.

• Forgot password ?
• Supporting professional practice
• Gifted and talented
• Problem Solving

Benefits of Problem Solving

The Ministry is migrating nzmaths content to Tāhurangi.             Relevant and up-to-date teaching resources are being moved to Tāhūrangi (tahurangi.education.govt.nz).  When all identified resources have been successfully moved, this website will close. We expect this to be in June 2024.  e-ako maths, e-ako Pāngarau, and e-ako PLD 360 will continue to be available. 

For more information visit https://tahurangi.education.govt.nz/updates-to-nzmaths

Using a problem solving approach to teaching and learning maths is of value to all students and especially to those who are high achieving. Some of the reasons for using problem solving are summarised below.

• Problem solving places the focus on the student making sense of mathematical ideas. When solving problems students are exploring the mathematics within a problem context rather than as an abstract.
• Problem solving encourages students to believe in their ability to think mathematically. They will see that they can apply the maths that they are learning to find the solution to a problem.
• Problem solving provides ongoing assessment information that can help teachers make instructional decisions. The discussions and recording involved in problem solving provide a rich source of information about students' mathematical knowledge and understanding.
• Good problem solving activities provide an entry point that allows all students to be working on the same problem. The open-ended nature of problem solving allows high achieving students to extend the ideas involved to challenge their greater knowledge and understanding.
• Problem solving develops mathematical power. It gives students the tools to apply their mathematical knowledge to solve hypothetical and real world problems.
• Problem solving is enjoyable. It allows students to work at their own pace and make decisions about the way they explore the problem. Because the focus is not limited to a specific answer students at different ability levels can experience both challenges and successes on the same problem.
• Problem solving better represents the nature of mathematics. Research mathematicians apply this exact approach in their work on a daily basis.
• Once students understand a problem solving approach to maths, a single well framed mathematical problem provides the potential for an extended period of exploration.

404 Not found

• Study Guides
• Homework Questions

Solving Problems Involving Measures of Position (Quartiles)

• Mathematics