problem solving inequalities

Solving Inequalities

Sometimes we need to solve Inequalities like these:

Our aim is to have x (or whatever the variable is) on its own on the left of the inequality sign:

We call that "solved".

Example: x + 2 > 12

Subtract 2 from both sides:

x + 2 − 2 > 12 − 2

x > 10

How to Solve

Solving inequalities is very like solving equations , we do most of the same things ...

... but we must also pay attention to the direction of the inequality .

Some things can change the direction !

< becomes >

> becomes <

≤ becomes ≥

≥ becomes ≤

Safe Things To Do

These things do not affect the direction of the inequality:

• Add (or subtract) a number from both sides
• Multiply (or divide) both sides by a positive number
• Simplify a side

Example: 3x < 7+3

We can simplify 7+3 without affecting the inequality:

But these things do change the direction of the inequality ("<" becomes ">" for example):

• Multiply (or divide) both sides by a negative number
• Swapping left and right hand sides

Example: 2y+7 < 12

When we swap the left and right hand sides, we must also change the direction of the inequality :

12 > 2y+7

Here are the details:

Adding or Subtracting a Value

We can often solve inequalities by adding (or subtracting) a number from both sides (just as in Introduction to Algebra ), like this:

Example: x + 3 < 7

If we subtract 3 from both sides, we get:

x + 3 − 3 < 7 − 3    

And that is our solution: x < 4

In other words, x can be any value less than 4.

What did we do?

And that works well for adding and subtracting , because if we add (or subtract) the same amount from both sides, it does not affect the inequality

Example: Alex has more coins than Billy. If both Alex and Billy get three more coins each, Alex will still have more coins than Billy.

What If I Solve It, But "x" Is On The Right?

No matter, just swap sides, but reverse the sign so it still "points at" the correct value!

Example: 12 < x + 5

If we subtract 5 from both sides, we get:

12 − 5 < x + 5 − 5    

That is a solution!

But it is normal to put "x" on the left hand side ...

... so let us flip sides (and the inequality sign!):

Do you see how the inequality sign still "points at" the smaller value (7) ?

And that is our solution: x > 7

Note: "x" can be on the right, but people usually like to see it on the left hand side.

Multiplying or Dividing by a Value

Another thing we do is multiply or divide both sides by a value (just as in Algebra - Multiplying ).

But we need to be a bit more careful (as you will see).

Positive Values

Everything is fine if we want to multiply or divide by a positive number :

Example: 3y < 15

If we divide both sides by 3 we get:

3y /3 < 15 /3

And that is our solution: y < 5

Negative Values

Well, just look at the number line!

For example, from 3 to 7 is an increase , but from −3 to −7 is a decrease.

See how the inequality sign reverses (from < to >) ?

Let us try an example:

Example: −2y < −8

Let us divide both sides by −2 ... and reverse the inequality !

−2y < −8

−2y /−2 > −8 /−2

And that is the correct solution: y > 4

(Note that I reversed the inequality on the same line I divided by the negative number.)

So, just remember:

When multiplying or dividing by a negative number, reverse the inequality

Multiplying or Dividing by Variables

Here is another (tricky!) example:

Example: bx < 3b

It seems easy just to divide both sides by b , which gives us:

... but wait ... if b is negative we need to reverse the inequality like this:

But we don't know if b is positive or negative, so we can't answer this one !

To help you understand, imagine replacing b with 1 or −1 in the example of bx < 3b :

• if b is 1 , then the answer is x < 3
• but if b is −1 , then we are solving −x < −3 , and the answer is x > 3

The answer could be x < 3 or x > 3 and we can't choose because we don't know b .

Do not try dividing by a variable to solve an inequality (unless you know the variable is always positive, or always negative).

A Bigger Example

Example: x−3 2 < −5.

First, let us clear out the "/2" by multiplying both sides by 2.

Because we are multiplying by a positive number, the inequalities will not change.

x−3 2 ×2 < −5  ×2  

x−3 < −10

Now add 3 to both sides:

x−3 + 3 < −10 + 3    

And that is our solution: x < −7

Two Inequalities At Once!

How do we solve something with two inequalities at once?

Example: −2 < 6−2x 3 < 4

First, let us clear out the "/3" by multiplying each part by 3.

Because we are multiplying by a positive number, the inequalities don't change:

−6 < 6−2x < 12

−12 < −2x < 6

Now divide each part by 2 (a positive number, so again the inequalities don't change):

−6 < −x < 3

Now multiply each part by −1. Because we are multiplying by a negative number, the inequalities change direction .

6 > x > −3

And that is the solution!

But to be neat it is better to have the smaller number on the left, larger on the right. So let us swap them over (and make sure the inequalities point correctly):

−3 < x < 6

• Many simple inequalities can be solved by adding, subtracting, multiplying or dividing both sides until you are left with the variable on its own.
• Multiplying or dividing both sides by a negative number
• Don't multiply or divide by a variable (unless you know it is always positive or always negative)

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons
• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

9.9: Solve Quadratic Inequalities

• Last updated
• Save as PDF
• Page ID 18867

Learning Objectives

By the end of this section, you will be able to:

• Solve quadratic inequalities graphically
• Solve quadratic inequalities algebraically

Before you get started, take this readiness quiz.

• Solve: \(2x−3=0\). If you missed this problem, review Example 2.2.
• Solve: \(2y^{2}+y=15\). If you missed this problem, review Example 6.45.
• Solve \(\frac{1}{x^{2}+2 x-8}>0\) If you missed this problem, review Example 7.56.

We have learned how to solve linear inequalities and rational inequalities previously. Some of the techniques we used to solve them were the same and some were different. We will now learn to solve inequalities that have a quadratic expression. We will use some of the techniques from solving linear and rational inequalities as well as quadratic equations. We will solve quadratic inequalities two ways—both graphically and algebraically.

Solve Quadratic Inequalities Graphically

A quadratic equation is in standard form when written as \(ax^{2}+bx+c=0\). If we replace the equal sign with an inequality sign, we have a quadratic inequality in standard form.

Definition \(\PageIndex{1}\): Quadratic Inequality

A quadratic inequality is an inequality that contains a quadratic expression. The standard form of a quadratic inequality is written:

\(\begin{array}{ll}{a x^{2}+b x+c<0} & {a x^{2}+b x+c \leq 0} \\ {a x^{2}+b x+c>0} & {a x^{2}+b x+c \geq 0}\end{array}\)

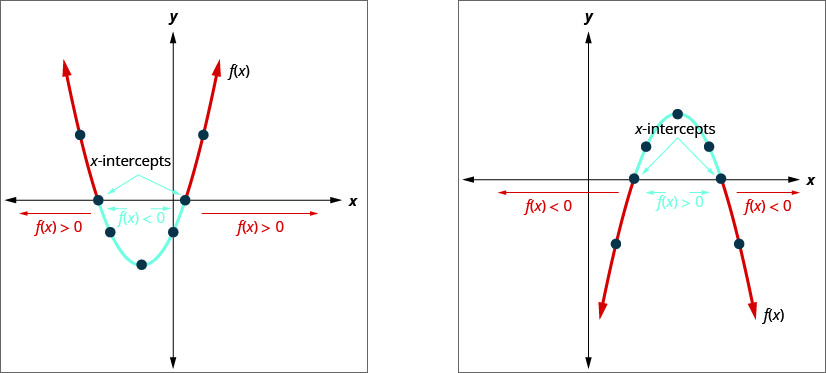
The graph of a quadratic function \(f(x)=a x^{2}+b x+c=0\) is a parabola. When we ask when is \(a x^{2}+b x+c<0\), we are asking when is \(f(x)<0\). We want to know when the parabola is below the \(x\)-axis.

When we ask when is \(a x^{2}+b x+c>0\), we are asking when is \(f(x)>0\). We want to know when the parabola is above the \(y\)-axis.

Example \(\PageIndex{1}\): How to Solve a Quadratic Inequality Graphically

Solve \(x^{2}−6x+8<0\) graphically. Write the solution in interval notation.

Step 1 : Write the quadratic inequality in standard form.

The inequality is in standard form.

\(x^{2}-6 x+8<0\)

Step 2 : Graph the function \(f(x)=a x^{2}+b x+c\) using properties or transformations.

We will graph using the properties.

\(f(x)=x^{2}-6 x+8\)

Look at \(a\) in the equation.

\(\color{red}{a=1, b=-6, c=8}\)

Since \(a\) is positive, the parabola opens upward.

The parabola opens upward.

The axis of symmetry is the line \(x=-\frac{b}{2 a}\).

Axis of Symmetry

\(x=-\frac{b}{2 a}\)

\(\begin{array}{l}{x=-\frac{(-6)}{2 \cdot 1}} \\ {x=3}\end{array}\)

The axis of symmetry is the line \(x=3\).

The vertex is on the axis of symmetry. Substitute \(x=3\) into the function.

\(\begin{array}{l}{f(x)=x^{2}-6 x+8} \\ {f(3)=(\color{red}{3}\color{black}{)}^{2}-6(\color{red}{3}\color{black}{)}+8} \\ {f(3)=-1}\end{array}\)

The vertex is \((3,-1)\).

We find \(f(0)\)

\(y\)-intercept

\(\begin{array}{l}{f(x)=x^{2}-6 x+8} \\ {f(0)=(\color{red}{0}\color{black}{)}^{2}-6(\color{red}{0}\color{black}{)}+8} \\ {f(0)=8}\end{array}\)

The \(y\)-intercept is \((0,8)\).

We use the axis of symmetry to find a point symmetric to the \(y\)-intercept. The \(y\)-intercept is \(3\) units left of the axis of symmetry, \(x=3\). A point \(3\) units to the right of the axis of symmetry has \(x=6\).

Point symmetric to \(y\)-intercept

The point is \((6,8)\).

We solve \(f(x)=0\).

\(x\)-intercepts

We can solve this quadratic equation by factoring.

\(\begin{aligned} f(x) &=x^{2}-6 x+8 \\ \color{red}{0} &\color{black}{=}x^{2}-6 x+8 \\ \color{red}{0} &\color{black}{=}(x-2)(x-4) \\ x &=2 \text { or } x=4 \end{aligned}\)

The \(x\)-intercepts are \((2,0)\) and \((4,0)\).

We graph the vertex, intercepts, and the point symmetric to the \(y\)-intercept. We connect these \(5\) points to sketch the parabola.

Step 3 : Determine the solution from the graph.

The inequality asks for the values of \(x\) which make the function less than \(0\). Which values of \(x\) make the parabola below the \(x\)-axis.

We do not include the values \(2\), \(4\) as the inequality is less than only.

The solution, in interval notation, is \((2,4)\).

Exercise \(\PageIndex{1}\)

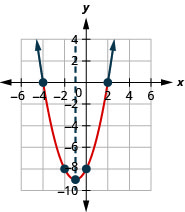
• Solve \(x^{2}+2 x-8<0\) graphically
• Write the solution in interval notation

Exercise \(\PageIndex{2}\)

• Solve \(x^{2}-8 x+12 \geq 0\) graphically

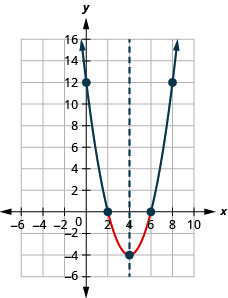
• \((-\infty, 2] \cup[6, \infty)\)

We list the steps to take to solve a quadratic inequality graphically.

Solve a Quadratic Inequality Graphically

• Write the quadratic inequality in standard form.
• Graph the function \(f(x)=ax^{2}+bx+c\).
• Determine the solution from the graph.

In the last example, the parabola opened upward and in the next example, it opens downward. In both cases, we are looking for the part of the parabola that is below the \(x\)-axis but note how the position of the parabola affects the solution.

Example \(\PageIndex{2}\)

Solve \(-x^{2}-8 x-12 \leq 0\) graphically. Write the solution in interval notation.

Exercise \(\PageIndex{3}\)

• Solve \(-x^{2}-6 x-5>0\) graphically

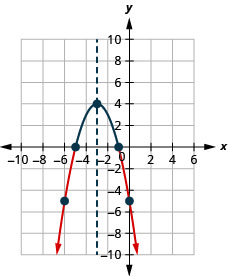
• \((-5,-1)\)

Exercise \(\PageIndex{4}\)

• Solve \(−x^{2}+10x−16≤0\) graphically

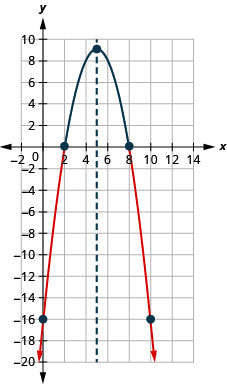
• \((-\infty, 2] \cup[8, \infty)\)

Solve Quadratic Inequalities Algebraically

The algebraic method we will use is very similar to the method we used to solve rational inequalities. We will find the critical points for the inequality, which will be the solutions to the related quadratic equation. Remember a polynomial expression can change signs only where the expression is zero.

We will use the critical points to divide the number line into intervals and then determine whether the quadratic expression will be positive or negative in the interval. We then determine the solution for the inequality.

Example \(\PageIndex{3}\): How to Solve Quadratic Inequalities Algebraically

Solve \(x^{2}-x-12 \geq 0\) algebraically. Write the solution in interval notation.

Exercise \(\PageIndex{5}\)

Solve \(x^{2}+2x−8≥0\) algebraically. Write the solution in interval notation.

\((-\infty,-4] \cup[2, \infty)\)

Exercise \(\PageIndex{6}\)

Solve \(x^{2}−2x−15≤0\) algebraically. Write the solution in interval notation.

In this example, since the expression \(x^{2}−x−12\) factors nicely, we can also find the sign in each interval much like we did when we solved rational inequalities. We find the sign of each of the factors, and then the sign of the product. Our number line would like this:

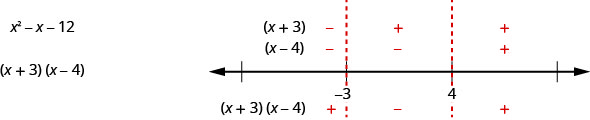
The result is the same as we found using the other method.

We summarize the steps here.

Solve a Quadratic Inequality Algebraically

• Determine the critical points—the solutions to the related quadratic equation.
• Use the critical points to divide the number line into intervals.
• Above the number line show the sign of each quadratic expression using test points from each interval substituted into the original inequality.
• Determine the intervals where the inequality is correct. Write the solution in interval notation.

Example \(\PageIndex{4}\)

Solve \(x^{2}+6x−7≥0\) algebraically. Write the solution in interval notation.

Exercise \(\PageIndex{7}\)

Solve \(−x^{2}+2x+1≥0\) algebraically. Write the solution in interval notation.

\([-1-\sqrt{2},-1+\sqrt{2}]\)

Exercise \(\PageIndex{8}\)

Solve \(−x^{2}+8x−14<0\) algebraically. Write the solution in interval notation.

\((-\infty, 4-\sqrt{2}) \cup(4+\sqrt{2}, \infty)\)

The solutions of the quadratic inequalities in each of the previous examples, were either an interval or the union of two intervals. This resulted from the fact that, in each case we found two solutions to the corresponding quadratic equation \(ax^{2}+bx+c=0\). These two solutions then gave us either the two \(x\) - intercepts for the graph or the two critical points to divide the number line into intervals.

This correlates to our previous discussion of the number and type of solutions to a quadratic equation using the discriminant.

For a quadratic equation of the form \(ax^{2}+bc+c=0, a≠0\).

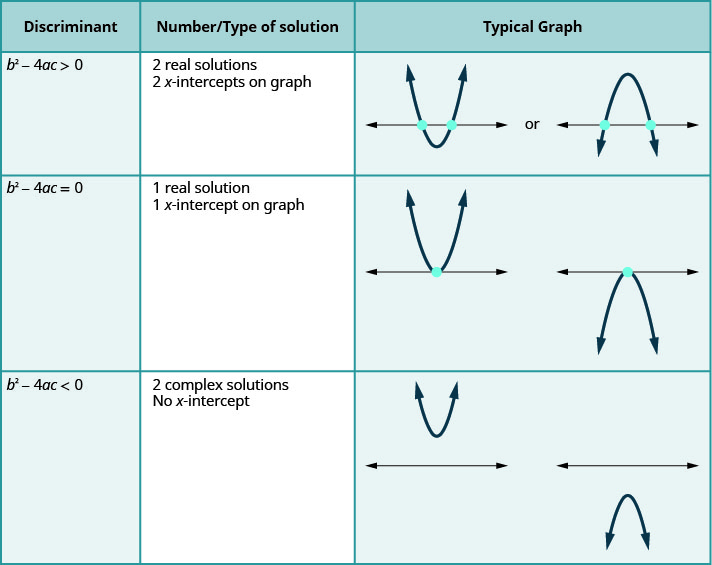
The last row of the table shows us when the parabolas never intersect the \(x\)-axis. Using the Quadratic Formula to solve the quadratic equation, the radicand is a negative. We get two complex solutions.

In the next example, the quadratic inequality solutions will result from the solution of the quadratic equation being complex.

Example \(\PageIndex{5}\)

Solve, writing any solution in interval notation:

• \(x^{2}-3 x+4>0\)

\(x^{2}-3 x+4 \leq 0\)

We are to find the solution to \(x^{2}−3x+4>0\). Since for all values of \(x\) the graph is above the \(x\)-axis, all values of \(x\) make the inequality true. In interval notation we write \((−∞,∞)\).

b. Write the quadratic inequality in standard form.

Determine the critical points by solving the related quadratic equation.

\(x^{2}-3 x+4=0\)

Since the corresponding quadratic equation is the same as in part (a), the parabola will be the same. The parabola opens upward and is completely above the \(x\)-axis—no part of it is below the \(x\)-axis.

We are to find the solution to \(x^{2}−3x+4≤0\). Since for all values of \(x\) the graph is never below the \(x\)-axis, no values of \(x\) make the inequality true. There is no solution to the inequality.

Exercise \(\PageIndex{9}\)

Solve and write any solution in interval notation:

• \(-x^{2}+2 x-4 \leq 0\)
• \(-x^{2}+2 x-4 \geq 0\)
• \((-\infty, \infty)\)
• no solution

Exercise \(\PageIndex{10}\)

• \(x^{2}+3 x+3<0\)
• \(x^{2}+3 x+3>0\)

Key Concepts

• Graph the function \(f(x)=ax^{2}+bx+c\) using properties or transformations.
• Determine the critical points -- the solutions to the related quadratic equation.